棒状柱塞气举液体漏失模型研究

师浩文，刘捷，罗威，丁晔，李锐，廖锐全

(1.长江大学 石油工程学院，湖北 武汉 430100；2.CNPC气举实验基地多相流研究室，湖北 武汉 430100；3.新疆油田公司 工程技术研究院，新疆 克拉玛依 834000)

引 言

由于地层能量的不断下降，使得井筒内的气体流速降低，气体携液能力随之减弱，当气相流速低于临界流速时，井筒中的积液无法被携带出井口，且在自身重力和气体滑脱的作用下，液体下落并积存于井底，形成井底积液从而造成气井停产，因此，需要采取合理的排水采气工艺将井底的积液及时排出，使气井复产。

柱塞举升技术作为经济性较高的排水采气技术在国内外已普遍应用。柱塞气举技术是在气相与液相的分界面上增加一个机械固体界面，并利用储层的自身能量将井底的积液举升至井口实现有效排液。该技术能够有效减少滑脱损失并提高举升效率。但在实际情况下，为实现柱塞在油管中往复运动，油管和柱塞间必然要存在一定宽度的环形间隙。在上行举液过程中，有些气体通过缝隙发生滑脱，也有一定量被举升的液体通过缝隙回落至井底。因此，有效减少液体回落，提高举液量成为柱塞气举工艺技术应用所面临的核心问题。针对柱塞气举漏失问题，国内外学者做了很多研究工作。Lee & Mower[1]在试验井中对常规柱塞气举液体漏失进行了研究，得到液体漏失与柱塞运动速度的关系曲线；Marsano[7]等基于动量守恒方程提出了常规柱塞举升设计模型，认为液体漏失速度是柱塞平均速度的函数；唐祖兵[2]等假设柱塞与油管壁间的流动为定常层流，基于上行液体质量和动量守恒原理建立了柱塞气举的液体漏失模型；Zhao Kunpeng[4]等对柱塞气举过程中柱塞速度、液体漏失的瞬态进行了理论和实验研究，建立了柱塞上方液柱质量和气体体积分数的瞬态模型。

本文通过室内实验模拟柱塞举升状态，考虑柱塞与油管轴线存在偏差且不平行对气举过程液体漏失的影响，建立柱塞与油管间环形空隙液体漏失的数学模型，并用实验数据在不同井斜状态下对模型进行验证。

1 柱塞气举漏失模型的建立

在斜井段柱塞气举过程中，油管与柱塞处于偏心状态。建立微元模型，x轴垂直于油管壁面，z轴为油管轴线，柱塞与油管间的环形间隙分别为δ1与δ2，渐扩楔形夹角为α，如图1所示。

柱塞在上升过程中运动过程较为复杂，并以非稳态流动为主。为了便于分析，在不影响对柱塞总体漏失的正确认识下，有必要作以下合理假设：

(1)流体流动为拟稳态流动；

(2)柱塞与油管间的环形空隙中，液体平行于管轴作直线流动；

(3)不考虑气体滑脱的影响；

(4)液体不可压缩。

在柱塞和管壁间取一个面积为dxdy，高度为dz的微元六面体微团，设柱塞上、下端面的压力分别为P、P+dP；微元体左、右两面所受到的表面摩擦切应力分别为τ、τ+dτ；微元体所受质量力为ρg，方向如图1所示。在均匀流动z方向上对表面力和质量力进行分析，通过受力分析可得

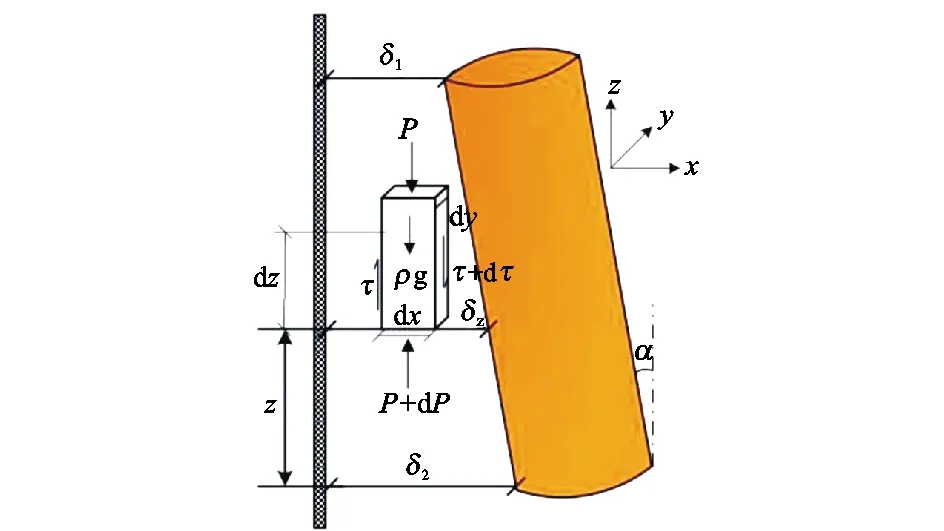
图1 柱塞气举间隙液体受力示意图

-Pdxdy+(P+dP)dxdy+τdydz-(τ+dτ)dydz-ρgdxdydz=0。

(1)

式(1)整理得

(2)

对于一维流动，所取微元体靠近下表面处，故其表面摩擦切应力为

(3)

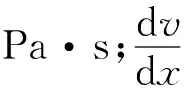
对摩擦切应力关于x求导，即

(4)

对速度积分得

(5)

柱塞上部液体漏失过程可以看作流体经过环形空隙的剪切-压差流动，即纯剪切流动与纯压差流动的叠加，如图2所示。压差流是指柱塞与油管壁间固定不动，间隙中的流体只在压差dP的作用下流动；剪切流动是指在柱塞两端压差作用下，内圆柱面和外圆柱面以速度vp沿油管轴线方向相对运动时，所引起的间隙中流体的流动。

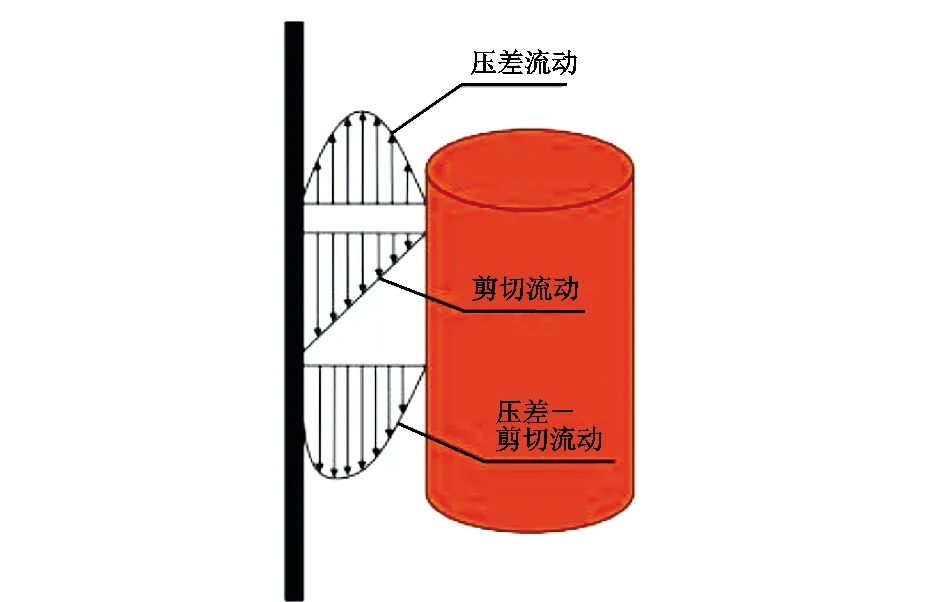
图2 柱塞-油管环形间隙内液体流场示意图

对式(5)进行纯压差流动和纯剪切流动的求解，并将二者的速度进行叠加，得

(6)

或

(7)

式中：v为液体漏失速度，m/s；vP为柱塞运动速度，m/s；dP/dz为压力降；ρ为液相密度，kg/m3；g为重力加速度，m/s2；lp为柱塞长度，m；σ为柱塞与管壁距离，m。

偏心配合的柱塞与油管沿垂直于x轴的任意截面，如图3所示。在间隙很小的情况下，缝隙的宽度为

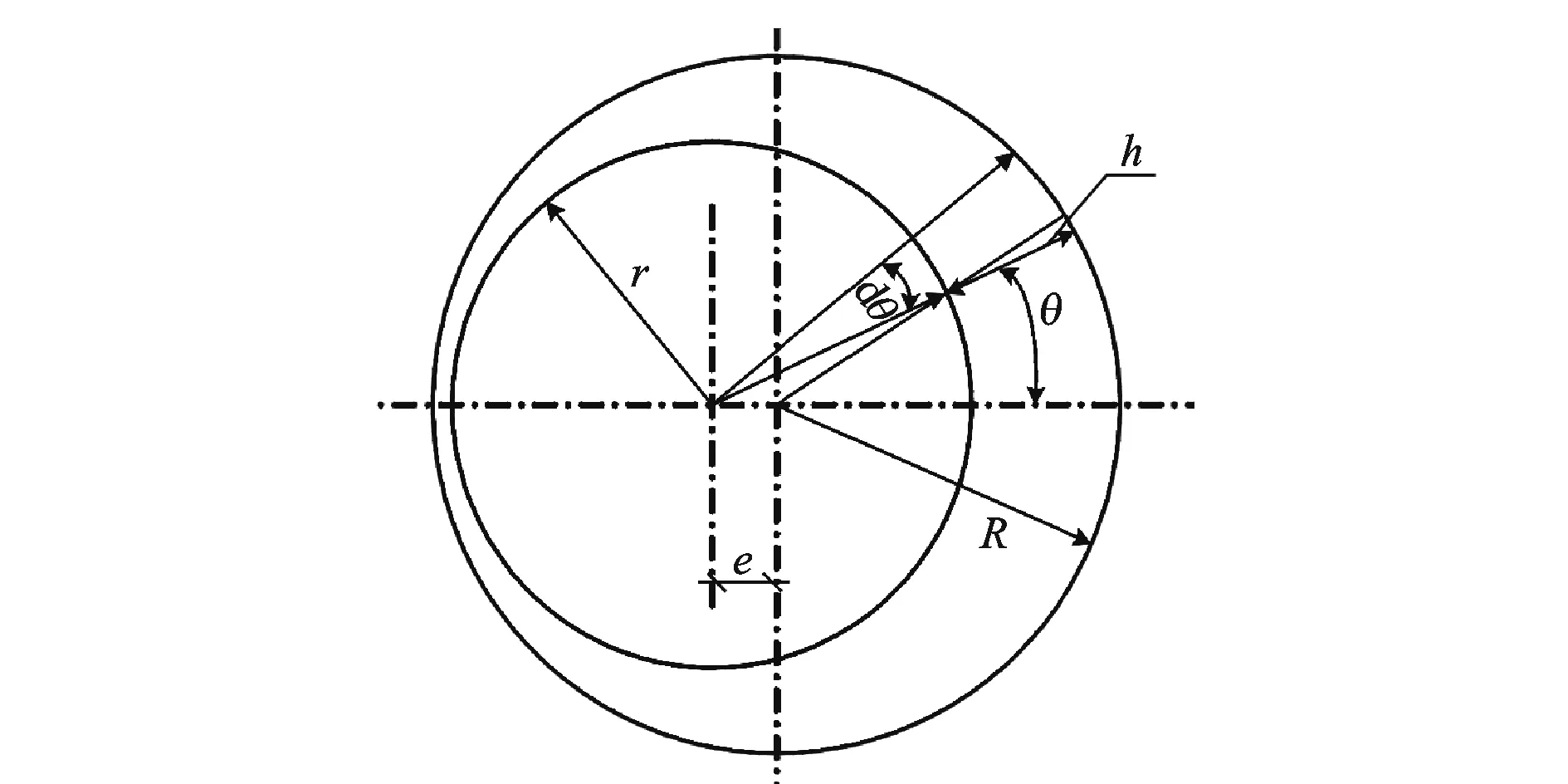
图3 偏心配合的柱塞与油管沿垂直于x轴的任意截面

h=(R-r)+ecosθ=δz+ecosθ。

(8)

因dQ=vRdθdx，由式(7)可得漏失量的计算公式为

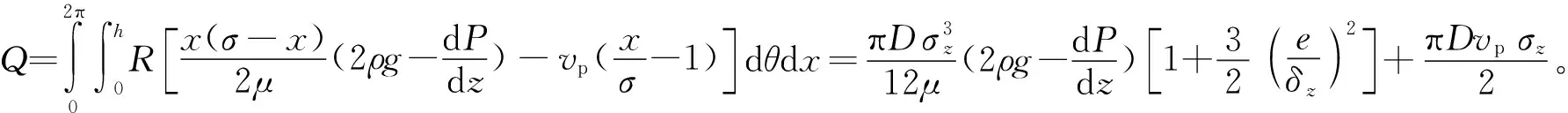
(9)

式中：h为间隙距离，m；R为管柱外径，m；σz为z方向上柱塞与管柱距离，m；e为偏心距，m；D为管柱内径，m；r为柱塞外径，m。因此，柱塞上下端面的压差ΔP为

(10)

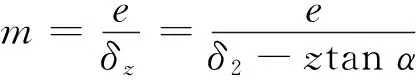
(11)

因此，偏心间隙液体漏失量qv的精确公式为

(12)

由于推导式(12)时，假设δ1≠δ2，e≠0，因此，式(12)不适用于δ1=δ2、e=0的情况，对于该情况，考虑到式(10)中1+1.5(e/δz)2项，在δ1≤δz≤δ2的范围内变化不大，1+1.5(e/δz)2≈1+1.5e2/(δ1δ2)，则漏失量qv的近似计算公式为

(13)

由式(13)可得，当偏心量e=0时，可以简化同心环形间隙漏失量的计算式；当δ1=δ2=δ时，可简化为仅考虑柱塞与油管在轴线平行时环形空隙间产生的漏失公式

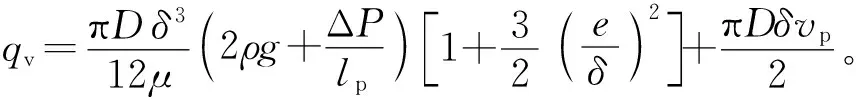
(14)

由于本文模型的柱塞为光滑且均匀的圆柱体，与实际的棒状柱塞有较大的区别，所以对棒状柱塞的研究需要在该模型下引入一个修正系数λ，即

(15)

则棒状柱塞的模型为

(16)

2 实验设备与方法

柱塞气举装置流程如图4所示。主要包括气路系统、液路系统、气液混合器、测试管段、气液分离器及数据采集系统。实验主要介质为压缩空气和自来水。实验流程如下：由空气压缩机(FHOGD-250/1.0)供给的气相流体，流经储气罐，进入空气干燥箱进行干燥。采用E+H气体流量计(流量34.72 m3/min，准确度±1%)测量气体质量流量。储液罐内的液相由柱塞泵抽汲，液相流体流经液相管线与气体一同进入混合器，同样采用E+H科氏力液体质量流量计(流量0～200 m3/h，准确度±0.3%)测量瞬时流量。在举升柱塞前，液相流体进入实验管段即无缝钢管内，逐渐形成井底积液；在举升过程中，液相与气相流体首先在混合器内混合，当达到井底流压理想值时，打开出口，随后在长10 m，内径为62 mm，壁厚为1 mm的测试管段内，柱塞在压差的作用下被推动上升。在实验管段的入口及出口处分别设置了压力测量点，采用北京力诺T351RD智能压力变送器(精准度0.5%)测量压力，采用北京力诺T351RD智能压差变送器(精准度0.025%～0.04%)测量压差。实验所用柱塞为双L型棒状柱塞，重2.5 kg，长0.45 m，直径58 mm。

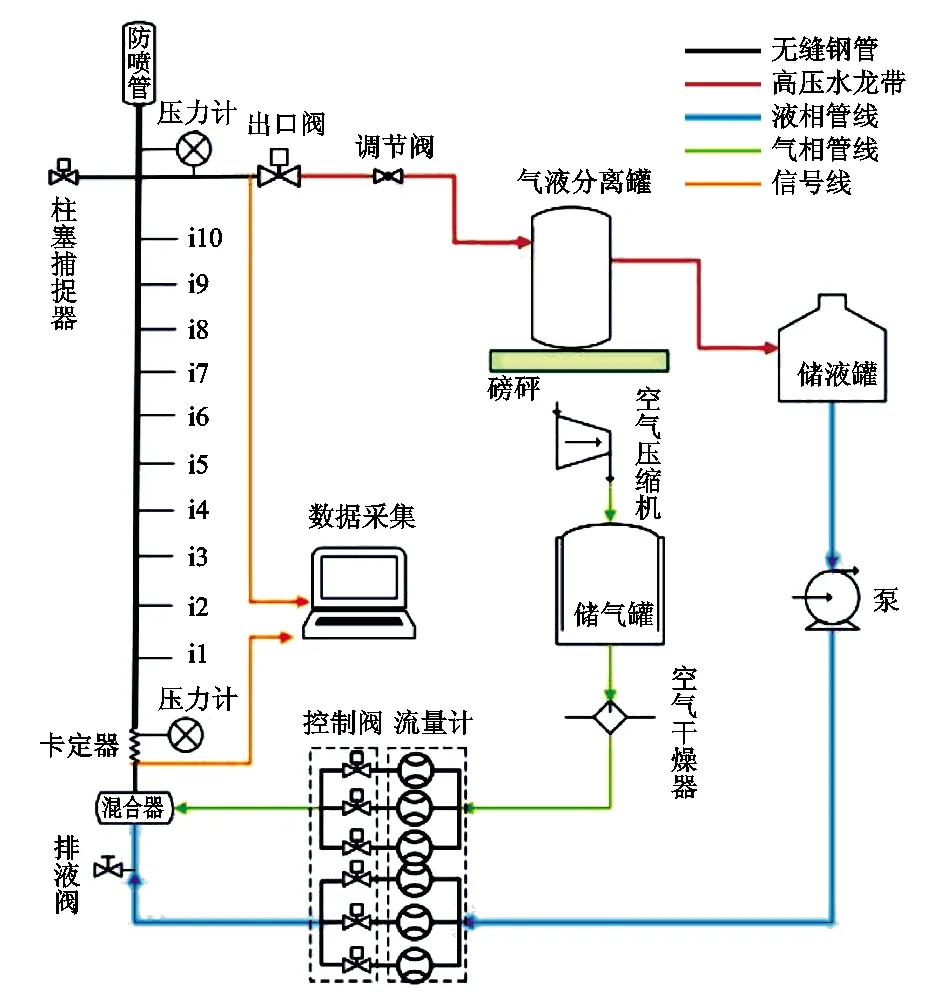
图4 柱塞气举实验流程

精确测量瞬时柱塞速度变化相当困难，为了能够准确研究柱塞在举升过程中的瞬态速度，采用地磁传感器进行准确的速度测量，在无缝钢管上布置10个地磁传感器，在图4中表示为从i1到i10。由于柱塞主要由钢铁制成，当柱塞通过地磁传感器时，地磁传感器会感应到外部磁场的变化，导致自身的电阻特性发生改变，从而产生电流并转化为电信号随后获得相应的运动时间。根据每个传感器间的距离和运动时间，能够准确地确定柱塞运动速度。

3 柱塞气举漏失实验结果

通过室内实验分别对直井和斜井进行数据测量，并对本文模型进行实验研究，测得实验相关参数，见表1。

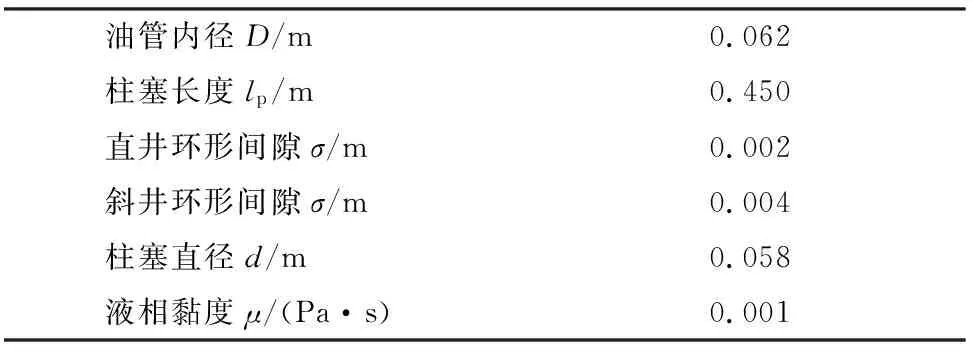
表1 实验相关参数

3.1 直井模型分析

在直井条件下，室内柱塞模拟实验测试了柱塞端面压差及柱塞运动时间。由式(14)计算得到的漏失量，并将室内实验得到的柱塞运动速度代入Lee & Mover等人在实际现场中所得到的漏失模型中进行计算，得到室内柱塞模拟实验条件下Lee & Mover模型的漏失量。运用Lee & Mover模型得到的室内实验漏失量除以式(14)的本文模型漏失量，得到修正量。直井漏失实验数据见表2。由表2可知，该修正量与柱塞运动速度密切相关，即可得到修正系数方程。对直井测得的数据与式(14)进行拟合，得到修正系数

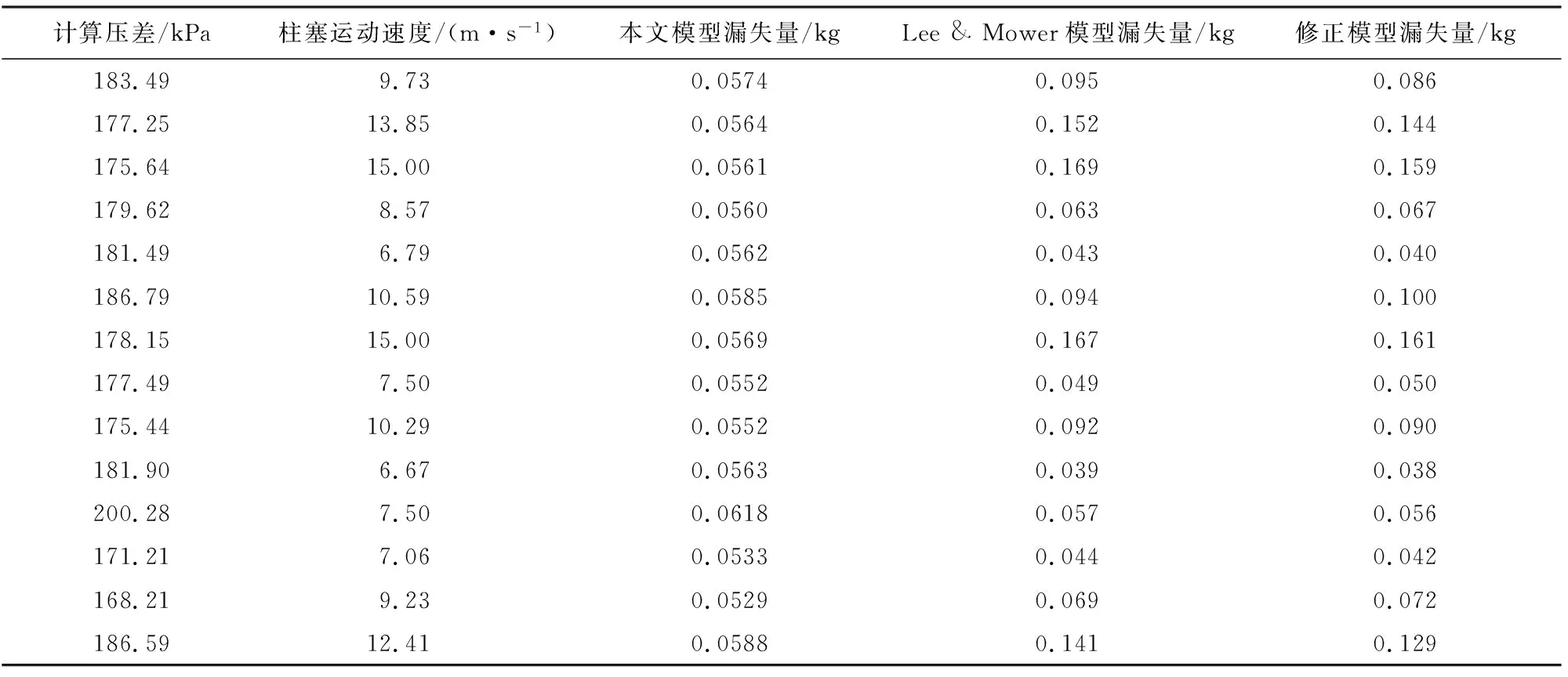
表2 直井漏失实验数据

λ=0.271 6vp-1.135 3。

(17)

则棒状柱塞通用模型为

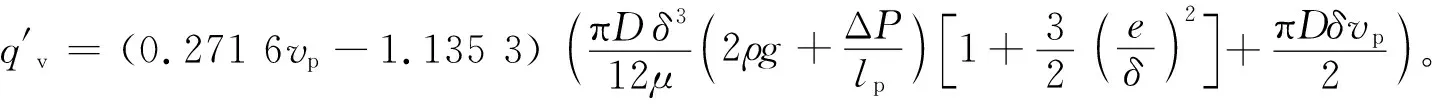
(18)

在直井条件下，e=0，则

(19)

将实验测得的速度与压差分别代入本文模型和Lee & Mower模型中得到漏失量的大小，并将两者进行对比验证，如图5所示。从图5可以看出，在本实验数据条件下，本文修正后的棒状柱塞模型与文献[1]的漏失模型计算得到的漏失量大小误差范围保持在±10%。表明本文修正后的模型能够较为精确地测量直井状态下的柱塞漏失量。

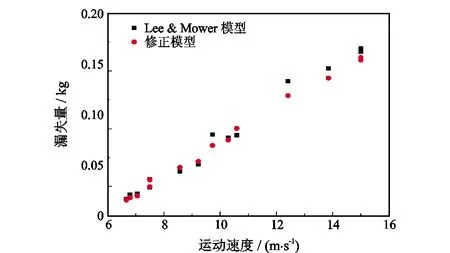
图5 修正模型与Lee & Mover模型误差对比

3.2 斜井模型分析

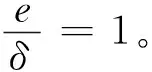
(20)

为了验证本文模型能够在斜井状态下得到良好的表达，进行了斜井状态下的室内漏失实验，并与修正模型进行对比验证，结果如图6所示。

从图6可以看出，不同井斜下，棒状柱塞漏失模型的漏失量与室内实验所测得的漏失量基本一致，表明本文棒状柱塞漏失模型具有一定的通用性与正确性。同时，当管柱处于倾斜状态时，漏失量会增多。经过分析，造成这种现象的原因是由于管柱倾斜时，柱塞紧贴管壁运动，与在垂直状态下的棒状柱塞有所不同，当井斜角不断增大时，与管柱轴线所平行的重力分量会逐渐增大，摩擦阻力造成柱塞上行困难。由式(20)可知，δ的大小间接影响着漏失量。当管柱倾斜时，直井时的环形间隙变为扇形间隙，造成气体滑脱的程度增大。并且，在液体自重影响下，有一定量的液体会通过扇形横截面自然下落。

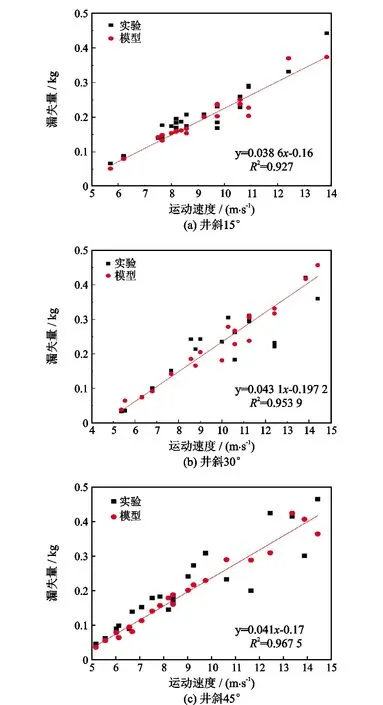
图6 不同井斜下修正模型与实验值对比

综上，管柱在井斜的状况下(0°～45°)，本文棒状柱塞漏失模型具有普适性；同时，模型与室内实验下计算所得的漏失量大小基本相同，并且漏失量均随着柱塞运动速度的增大而增大。表明漏失量大小直接受到柱塞运动速度影响。同时，在现场实际中，通过延长关井时间来获得较大举升效率是不可取的。

4 结 论

(1)从本文漏失模型可知，液体漏失主要受到柱塞运动速度及开井后柱塞上下端面压差的影响，柱塞运动速度随着柱塞上下端面压差的增大而增大，最终造成漏失量增加。

(2)直井状态下，棒状柱塞修正模型与Lee & Mower模型的误差范围在±10%以内，同时，本文模型能够较为准确地计算斜井时液体漏失量大小。

(3)本文模型只考虑了棒状柱塞下的漏失修正系数，使得棒状柱塞漏失模型具有一定的通用性。同时，在使用不同类型柱塞时应考虑引入不同的漏失系数进行修正。