最大化夏普比率的交替方向乘子法
刘媛媛,韦增欣,李峥嵘
(广西大学 数学与信息科学学院, 广西 南宁 530004)
0 引言
夏普比率是威廉夏普[1]为研究衡量基金绩效表现而指出的一个指标,此指标不仅是一个基金绩效评价标准化指标,且是一个可以同时对收益与风险加以综合考虑的三大经典指标之一。由于夏普比率在多领域的成功应用,威廉夏普成为了诺贝尔奖获得者,然而如何寻求最大化非凸函数夏普比率的最优解是一个问题。
近年来,学者们使用夏普比率构建投资组合[2]、衡量市场共同基金的表现[3]、评价信息检索系统性能[4]。夏普比率有一个很好的多面体的可行域, 但是它的目标函数比较复杂, 不易求解, 考努江斯[5]从优化的角度对夏普比率进行了理论分析, 然而并没有设计优化算法对其进行求解以及实证分析。
ADMM(alternating direction method of multipliers)算法最早分别由GLOWINSKI等[6]以及GABBY等[7]提出, BOYD等[8]对ADMM算法进行了相关的综述, 阐述了ADMM算法如何通过分解问题, 再逐一求解单个优化问题的基础上求解问题, 文章也证明了ADMM算法适用于大规模分布式优化问题, 而后证明了无松弛因子算法的收敛性。ADMM的应用领域十分广泛, 最早使用其求解单调变分不等式[9-11], 近年来, ADMM算法主要应用在电力系统、图像处理等方面[12-17], 然而在金融领域还没有得到广泛应用和重视。
笔者在考努江斯[5]证明了夏普比率可以转化成为凸优化问题的基础上, 使用ADMM算法对夏普比率进行求解, 因松弛因子对算法收敛性有影响, 故考虑改进算法找到使ADMM算法收敛最快的松弛因子, 为了验证其有效性, 在实证分析中将其与其他常见求解凸规划的算法进行比较。
1 使用ADMM算法改写夏普比率
1.1 夏普比率的等价转化
最大化夏普比率的投资组合可以通过求解以下问题得到
(1)
其中,μ=(μi)n,μi表示第i个资产的收益,x=(xi)n,xi表示第i个资产占总资产组合的比例,Σ表示投资组合的协方差。问题(1)不是一个凸规划问题,可将问题(1)进行转化得到等价的二次规划问题,以此直接获得最优风险投资组合。
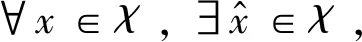
(2)
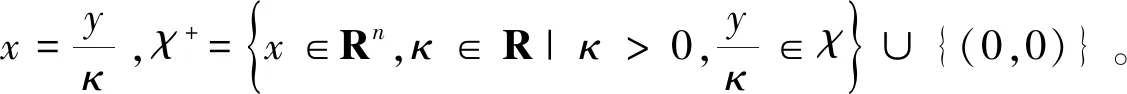
证明假设①和假设②保证了所有的可行投资组合都是有意义的,假设③保证了投资组合的协方差矩阵为正定矩阵,若资产A与资产B的收益之间存在完全的函数关系,此时在A、B中选择一个收益高而风险低的进行投资即可。
对满足假设②μTx>rf的可行解x以及问题(1)中的变量做如下改变:
(3)
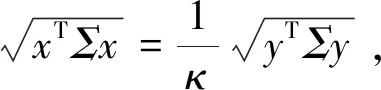
(4)

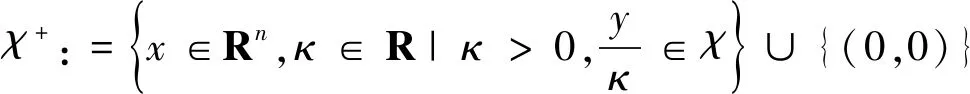
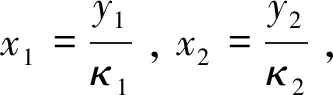
(5)
有
(6)
又显然λκ1+(1-λ)κ2>0,故得证。
定理1问题(2)的目标函数是凸二次函数,约束区域为凸。此问题可以使用ADMM算法求解。
1.2 夏普比率等价问题的ADMM形式
引理3(μ-rfe)Ty=1可改写成Ay=b,其中:
(7)
引理4引理3中的A可逆。
证明因为μTx>rf,因此必然存在一个μk,k=1,2,…,n,使得μk≠rf,不失一般性可以假设μ1-rf≠0,那么|A|≠0,即A可逆,那么通过计算得到
(8)
得证。
引理5问题(2)的ADMM形式可以表示为
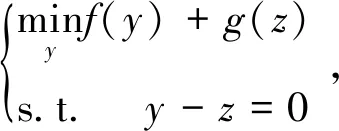
(9)
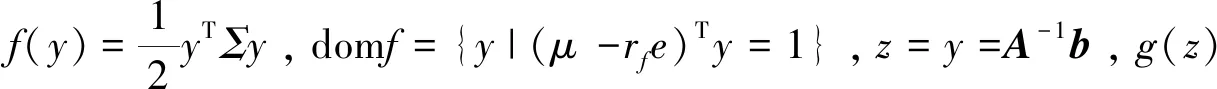
问题(9)的ADMM的尺度化的形式包含以下迭代:
yk+1∶=(Σ+ρI)-1[-ρ(uk-zk)],zk+1∶=yk+1+uk,uk+1∶=uk+yk+1-zk+1,
(10)
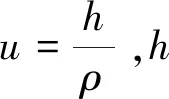
定理2添加松弛因子的ADMM算法的尺度化的形式包含以下迭代:
yk+1∶=(Σ+ρI)-1[-ρ(uk-zk)],zk+1∶=αyk+1+(1-α)zk+uk,uk+1∶=uk+α(yk+1-zk+1),
(11)
根据文献[18]的实验可知松弛变量α∈[1.5,1.8]可以改善收敛,为了加快算法在解决本问题时的收敛速度,这里考虑寻找一个合适的松弛因子。
1.3 改进ADMM算法并寻找加快收敛速度的松弛因子
α和ρ的取值可能对算法的结果产生一定的影响,因此增加α和ρ循环,根据ρ变化时不同松弛因子下的终止迭代次数,找到使得迭代加快的松弛因子。以下是算法的基本流程:
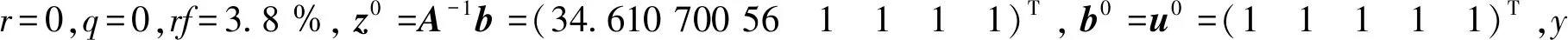
Step 1:设置ρ根据步长为0.1循环;
Step 2:设置α根据步长为0.01进行循环;
Step 3:设置迭代次数k以步长为1进行循环;
Step 4:根据z0、u0使用式(11)计算yk、zk、uk;
Step 5:若此时yk、zk、uk满足终止条件,输出迭代次数k,回到step 2,直到step 2循环完毕回到step 1,step 1循环完毕跳出循环,输出矩阵ali、kit; 若此时yk、zk、uk不满足终止条件,则回到step 4计算yk+1、zk+1、uk+1。
1.4 ADMM算法的收敛性证明
定理3设L0的鞍点为(y*,z*,h*),并定义P*=f(y*)+g(z*),Pk=f(yk)+g(zk),rk+1=yk+1-zk+1。当α∈(0,2)时,算法收敛到最优解,即
(12)
证明f(y)是Gateaux可微的并且是一致凸函数,根据Glowinski[6]可以得
(13)
因为L0的鞍点为(y*,z*,h*),显然,L0(y*,z*,h*)是有限的,并且(y*,z*)是原问题的最优解,那么就有y*-z*=0,并且f(y*)<∞,g(z*)<∞,h*是对偶问题的最优解。
根据L0(y*,z*,h)≤L0(y*,z*,h*)≤L0(y,z,h*)有
f(y*)+g(z*)+(h*)T(y*-z*)≤f(yk+1)+g(zk+1)+(h*)T(yk+1-zk+1),
(14)
将y*-z*=0,P*=f(y*)+g(z*),Pk=f(yk)+g(zk)代入式(14)则有
P*-Pk+1≤(h*)Trk+1,
(15)
由yk+1=argminyLρ(y,zk,hk),则有
0∈∂f(yk+1)+hk+ρ(yk+1-zk),
(16)
由hk+1=hk+αρ(yk+1-zk+1),得到hk=hk+1-αρ(yk+1-zk+1),代入式(16)有
0∈∂f(yk+1)+[hk+1+ρ(αzk+1-zk)+ρ(1-α)yk+1],
(17)
对式(17)求以y为变量的原函数,则有
(18)
同理zk+1=argminzLρ(yk+1,z,hk),则有
(19)
根据式(18)、(19)有下式成立:
(20)
(21)
将式(20)、(21)相加后,再将y*-z*=0,yk+1-zk+1=rk+1代入,所得结果与式(15)联立得到
-(h*)Trk+1≤Pk+1-P*≤-(hk+1)Trk+1-ρ(αzk+1-zk)T[rk+1+(zk+1-z*)]-

(22)
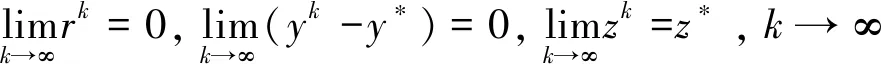
得证。
2 实证分析
针对建立的模型,给出下面的数值算例以验证模型有效性,同时选取可以加快收敛速度的拉格朗日乘子、松弛因子,并且将ADMM算法与常用的算法比较,验证ADMM算法收敛速度的快慢。这里通过同花顺软件选取5支股票,收集这5支股票在2017年的月收益率数据,如表1所示。

表1 5支股票月收益率
经过计算其协方差矩阵的特征值皆为正数,因此协方差矩阵是正定的,可以使用ADMM算法求解。这里选取招商银行2017年3月10日发售的储蓄国债(凭证式)三年期票面利率3.8 %为无风险利率,即rf=3.8 %,那么:
(24)
这里先将问题(2)转化成无约束问题(25):
(25)
问题(2)与问题(25)等价。根据初始值,图1给出了改进后的ADMM算法在ρ∈(0.1,1)时不同松弛因子下的终止迭代次数。
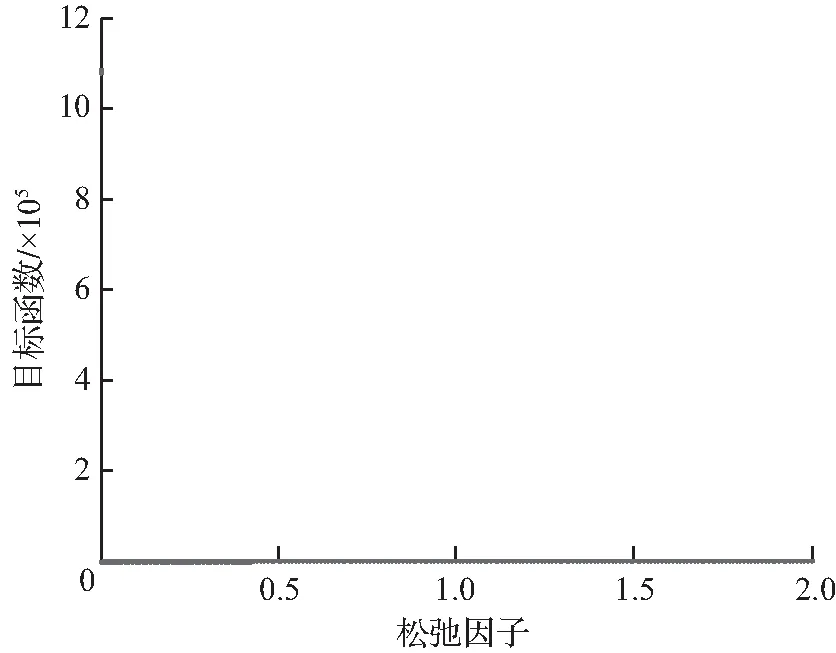
(a) 不同拉格朗日参数的目标函数值随松驰因子变化图
图1(b)中的离散点组成的曲线从下往上表示以0.1为步长ρ∈(0.1,1)的图像,从图1可以看出,目标函数值都达到了最优点,迭代次数可用来衡量迭代速度的快慢;α在1.8附近时,迭代速度相对较快,并且此时拉格朗日乘子取值对迭代速度的影响没有太大区别。
根据上述结论,后面在进行比较时参数取ρ=0.5,α=1.8可以加速迭代速度。此时求出问题(2)中的解:
κ=0.000 998 881。
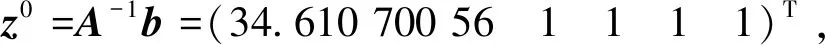
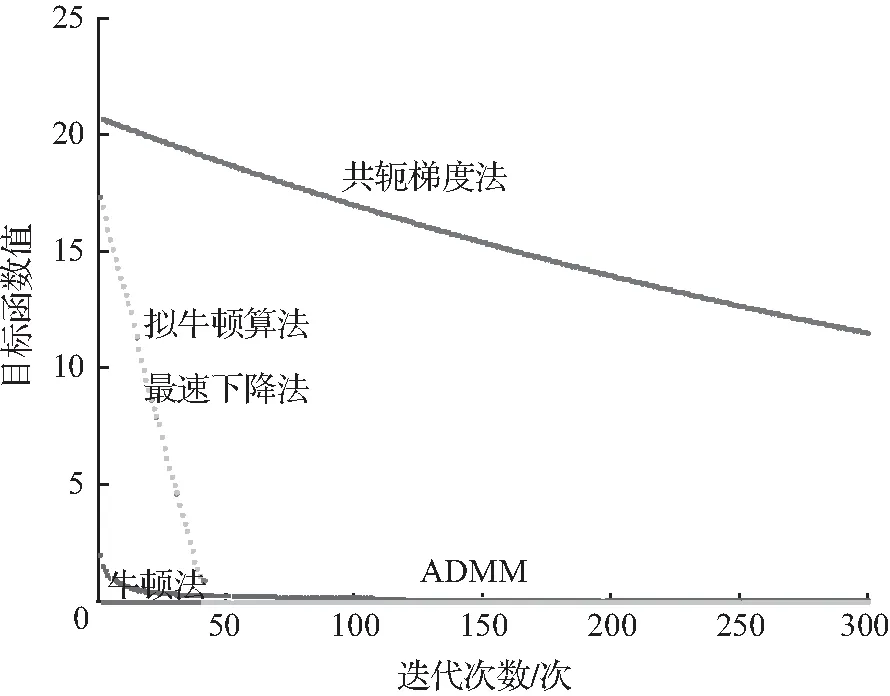
图2 不同迭代次数下各个算法的目标函数值变化情况
3 结语
ADMM是目前比较成熟,且比较受欢迎的约束问题最优化通用框架,它将许多经典优化思路整合、将一个问题分成可分布式的同时对多个小问题交替求解,使得问题得以解决。将ADMM算法运用于求解夏普比率,从数学的角度来求解金融问题,并且通过数值实验对算法的有效性进行了验证。在实证分析中考虑了维数为五的低维情况,而ADMM算法更适用于求解大规模分布式优化问题以及数据集较大的统计学、机器学习的相关问题,因此在下一步将考虑维数更高的情况,验证ADMM算法在高维环境下的可行性、有效性以及优势。

