一个共轭梯度算法与随机两人零和博弈分析

李向荣，黎鹏，卢俊宇，袁功林*

(1.广西大学 数学与信息科学学院， 广西 南宁 530004; 2.广西大学 商学院， 广西 南宁 530004)

0 引言

考虑如下的最优化问题：

min{f(x)∣x∈Rn},

(1)

其中f:Rn→R并且f∈C2。求解该该模型的方法有牛顿法、拟牛顿法、信赖域方法和共轭梯度法等，其中共轭梯度法因结构简单，存储量小被广泛使用。常见的求解问题式(1)的共轭梯度算法迭代公式为

xk+1=xk+αkdk,

(2)

其中,xk是当前迭代点，dk是搜索方向，αk为沿着搜索方向的步长，k=0,1,2,…。搜索方向dk定义如下：

(3)

其中，βk∈R，不同的βk决定不同的共轭梯度算法[1-9]。著名的PRP算法公式[10-11]中βk有如下形式：

(4)

其中，gk=g(xk)=f(xk)，gk+1=g(xk+1)=f(xk+1)分别是xk和xk+1处的梯度。PRP算法能有效处理大规模优化问题，并且数值表现优越，但其收敛性不理想。如在下列弱Wolfe-Powell(WWP)线搜索下，它不能满足非凸函数的全局收敛性。

(5)

和

(6)

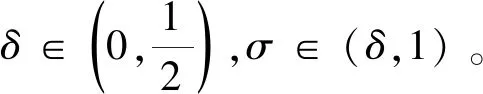
(7)

和

(8)

① 搜索方向满足充分下降性;

② 在YWL线搜索下新算法对一般函数具有全局收敛性;

③ 对大规模优化问题来说新算法比PRP算法优秀。

本文所用记号如下：gk为目标函数，f(x)在点xk处的梯度，‖·‖为向量的欧氏范数。

1 目标与算法

PRP算法对一般方程来说不满足全局收敛性的一个重要原因在于它不具有充分下降性，TOUATI-AHMED等[13], AL-BAALI[14], GILBERT等[15], HU等[16]表明了对共轭梯度法来说充分下降性是保证全局收敛性的关键。而王博朋等[17]提出了如下的一种三项共轭梯度法公式的搜索方向：

(9)

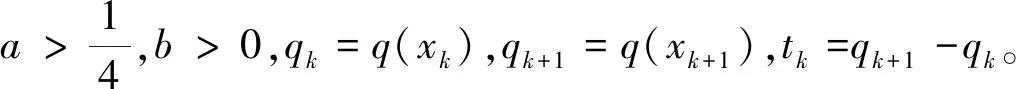
上述算法能求解如下的非线性方程组：

q(x)=0,x∈Rn，

(10)

其中，q:Rn→Rn连续可微且单调。笔者发现其中的qk是一个n维向量，是该非线性方程组的解，使得q(x)=0。考虑如式(1)无约束优化问题中的g(x)→0，这两者之间是否有联系，下面就来证明一下。

算法(1)步骤如下：

Step1:给定初始点x0∈Rn,ε∈(0，1)，δ∈(0，1/2)，δ1∈(0，δ)，σ∈(δ，1)，令k=1。

Step3:用YWL线搜索选出αk。

Step4:令迭代公式为xk+1=xk+αkdk。

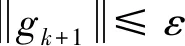
Step6:通过:

(11)

Step7:令k:=k+1并且转到step 2。

2 下降性和收敛性的证明

为了证明算法(1)的全局收敛性，现提出必要的假设条件:

假设1：① 水平集Ω={x∈Rn|f(x)≤f(x0)}是有界的。

② 函数f有下界，可微，还满足Lipschitz连续，即

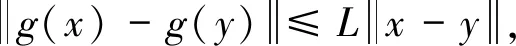
(12)

成立，并且L>0是一个常数。现在需证明关于式(11)的搜索方向dk的充分下降性。

引理1搜索方向dk由式(11)定义，则下面的结论成立：

(13)

其中,0<η≤1是一个常数。

(14)

得证。

(15)

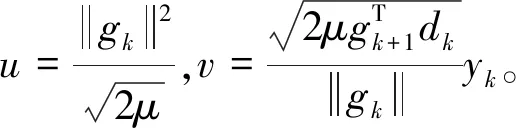
引理2由式(11)定义的dk有下面的结论:

(16)

其中,c是一个常数。

证明

(17)

由上知引理2得证。接下来的定理是关于算法的全局收敛性。

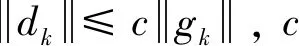
(18)

证明通过式(8)、(13)，可以有

(19)

通过式(12)，有

(20)

所以可以得到

(21)

通过假设1，式(7)、(12)、(18)得到

(22)

总结上述不等式从k=0到∞，可以得到

(23)

(24)

(25)

3 数值试验

数值实验由两部分组成, 一是图像修复处理实验, 二是验证随机两人零和博弈模型。实验具体设置如下：

实验参数：δ=0.2,δ1=0.5,σ=0.85,μ=0.5,γ=0.8。

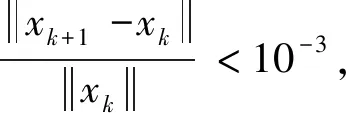
数值实验中所有的代码都在Matlab R2014b上编写,运行环境为8 G 内存, 2.30 GHz CPU Windows 10操作系统。

3.1 图像处理

在图像处理实验中, LL算法和PRP算法将对被脉冲噪声破坏的图像恢复原始图像。图像修复工作在优化领域具有重要的现实意义, 能体现出共轭梯度法在实际应用中起到重要的作用。

实验选择Lena (512×512)、Baboon (512×512) 和Man (512×512)作为测试图像。图 1、图 2给出了详细的性能结果。可以看出LL 算法、 PRP 算法都对测试图像的影像复原有效。表1中列出了CPU时间的消耗,以比较目的在于LL 算法和PRP算法在图像处理方面的优劣。

(a) 测试图像Lena

(a) 测试图像Lena

表1 LL算法，PRP算法基于30 %噪声修复图像使用CPU时间

表2 LL算法，PRP算法基于50 %噪声修复图像使用CPU时间

从表1、表2、图 1和图 2可以得出结论: ①当测试图像含有50 %噪声时,比含有30 %噪声的图像恢复所需的CPU 时间较多; ②当噪声率增加时,恢复图像所需要的时间也随之增加。③LL算法比 PRP 算法所需CPU时间更少，更适用于影像复原问题。

3.2 随机两人零和博弈模型实验

零和博弈又被称为游戏理论或零和游戏,是指一项游戏中, 游戏者有输有赢, 一方所赢正是另一方所输, 而游戏的总成绩永远为零。零和博弈之所以广受关注, 主要是因为人们发现社会的方方面面都能发现与零和博弈类似的局面, 从个人到国家, 从政治到经济,似乎无不验证了世界正是一个巨大的零和博弈场。零和博弈是博弈过程的最基本模型, 理想的零和博弈对于金融市场有重要意义, 在金融市场实际趋势运行中, 理想零和博弈的全过程接近于一个半圆。理想零和博弈, 从金融趋势的演变角度来看, 最终将构成核心因子。混沌经济学研究者一直希望在证券市场寻找到主宰世界命运的“混沌因子”, 事实上, 所有金融市场的“混沌因子”就是这么一个理想零和博弈的半圆。在这一部分中,笔者研究了一类两人零和随机博弈模型, 其中通过连续时间马尔可夫过程给出了具有两个随机动力系统[z(t),v(t)]的参与人1和参与人2。 在每个时间t, 对所有参与人的收益函数[18]定义为ψ[t,z(t),v(t),i],i=1, 2。参与人i通过如下一个满足耦合偏微分方程鞍点的均衡策略, 最大化的期望收益函数定义为

γi[zψz(i)+vψv(i)]+μi[ψ(j)-ψ(i)]},

(26)

其中,j≠i,i,j=1,2,κ(i) 代表运行成本,ζi,ρi,ηi,γi,δi代表参数,ζi,μi是控制变量, 后缀代表ψ对空间变量(z,v) 和时间变量t的导数。与许多偏微分方程类似, 耦合偏微分方程 (26)具有终端条件：

ψ(T,z(t),v(t),i)=π(T,z,v),

(27)

以及下列边界条件:

(28)

状态1：

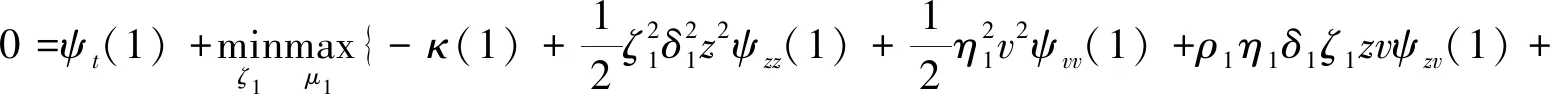
(29)

状态2：

(30)

问题(29)、(30)分别具有i=1和i=2 的边界条件 (28) 和终端条件 (27)。这两个问题都需要控制变量ζi,μi(i=1,2)。问题(29)和(30)称为二阶偏微分方程, 其中含有一阶偏微分项ψt,ψv,ψz,ψtvv,ψzz,ψzv。下面列出有限差分公式[19], 这些公式将在程序中用到：

(31)

(32)

(33)

(34)

(35)

(36)

(37)

其中,λ为指示函数,定义如下:

(38)

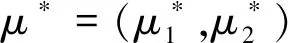
(39)

和

(40)

本文的目标是通过LL算法获得式(39)、(40)的最优(或近似)解ζ1和ζ2。在本次实验中, 成本函数κ=0,μ1∈(0.04,0.14),μ2∈(0.15,0.24),ρ1=ρ2=0.3,δ1=0.1,δ2=0.3,η1=0.25,η2=0.45,γ1=0.03,γ2=0.01,M=100, 终端时间T= 1,τ=0.02。空间参数(z,v)被放置到一个正方形[0,zmax]×[0,vmax]中, 初始对(z0,v0)=(1,1), (zmax,vmax)=(20,20)、 (30,30) 、(100,100)分别进行求解,详细结果如图 3至图5。

图3 20个离散点时的表现(t=0.8)

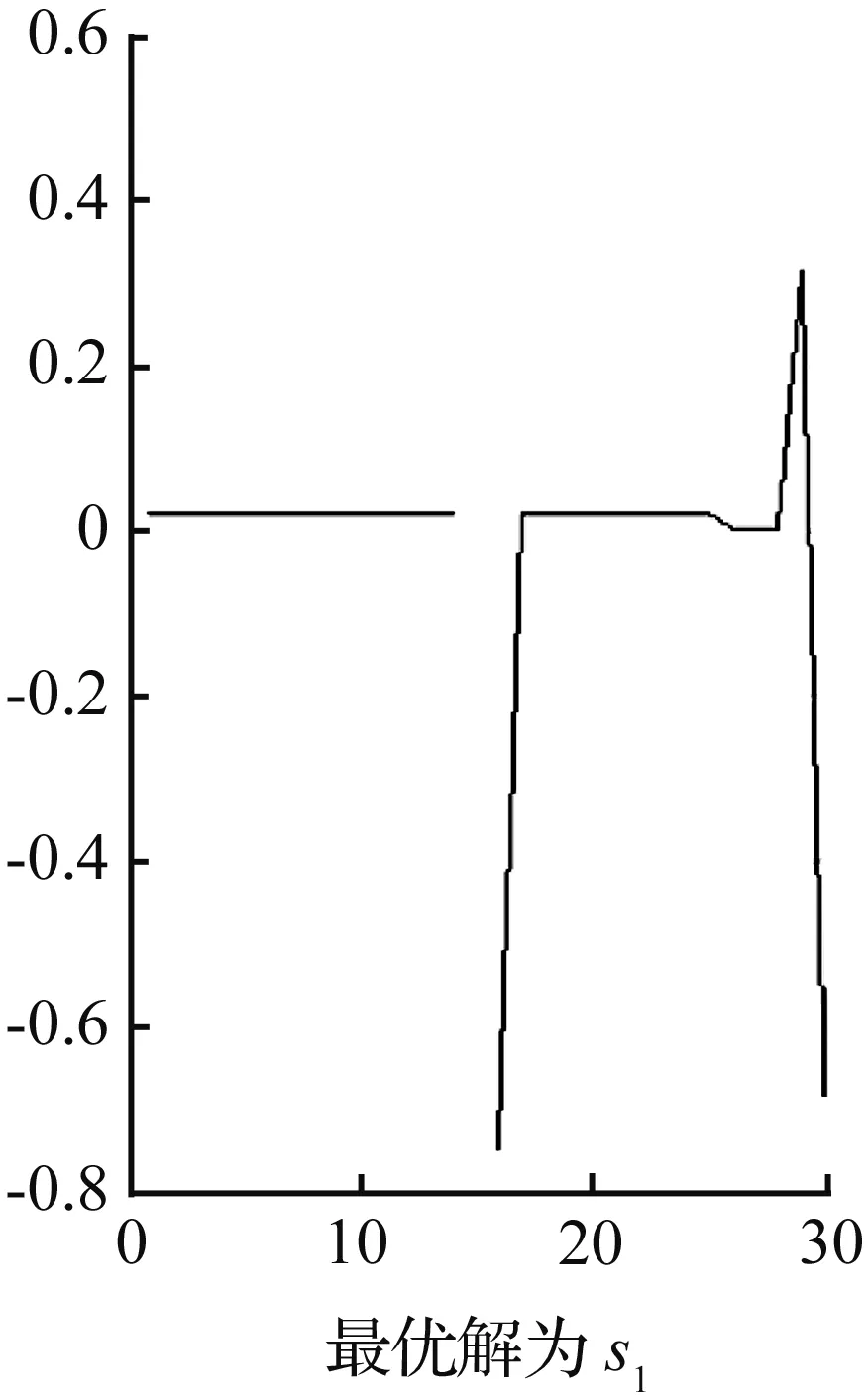
图4 30个离散点时的表现(t=0.8)

图5 100个离散点时的表现(t=0.8)

从图3至图5可以看出, 控制变量ζ1∈[-1,1],ζ2∈[-1,1]是成立的, 同模型规定的变量范围相符, 因而可以得出建议的算法对时间变量t=0.8而言, 至少能成功求解出离散点个数为20, 30和100的情形,验证了算法的有效性。关于其他时间点t以及更多离散点情况,有待进一步验证。

4 总结与展望

对于求解无约束优化问题，笔者根据文献[21]的启发，在求解无约束问题时应用了文献中的方向，验证该算法在能求解非线性方程组问题时, 能否求解无约束优化问题，并在一定条件下，证明了算法的充分下降性和全局收敛性等算法性质。同时在数值实验结果中通过对比，确定本文所提算法比PRP算法有效。

笔者相信，随着社会的高速发展，无约束最优化的问题会被人们更加重视，会有越来越多的学者投入到无约束问题的研究中，无约束问题的研究将会在21世纪取得长足的进步。