基于ITD与改进MCKD的滚动轴承故障诊断方法

刘丰，李欣欣，黄河，郭思远，李金明，黄振峰，毛汉领

(广西大学 机械工程学院， 广西 南宁 530004)

0 引言

滚动轴承表面的早期局部故障出现时，故障冲击成分通常比较微弱，特征表现并不明显；同时，滚动轴承微弱故障产生的振动信号会被大量的由设备和环境等因素产生的冗余噪声所淹没[1]。因此，实现微弱故障信号的增强，进而有效提取故障特征信息是滚动轴承早期故障诊断的技术关键[2-3]。

轴承故障产生的振动信号通常是非线性、非平稳的，时频分析方法为处理这种信号提供了重要手段。目前常用的时频分析方法主要有短时傅里叶变换、Wigner-Ville 分布、小波变换等，但这些方法都缺乏一定的自适应性[4]。经验模态分解(empirical mode decomposition, EMD)虽具有自适应性，但该方法理论不完善且存在过包络、欠包络、端点效应、频率混淆等问题[5-6]。FREI等提出了一种固有时间尺度分解[7](intrinsic time scale decomposition， ITD)的自适应信号时频分析法，克服了EMD的边缘效应等缺点且具有较高的计算效率。最近，ITD已在轴承故障诊断中得到广泛应用。YUAN等[8]采用平滑ITD处理振动信号，克服了噪声的影响，同时借助多重分形去趋势波动分析提高了故障识别精度。刘嘉辉等[9]对轴承故障信号进行ITD分解，并将分量重组解混，经全矢谱分析实现了故障特征提取。关焦月等[10]利用ITD结合多尺度形态滤波方法对故障信号进行降噪处理，提取了故障特征信息。

在滚动轴承故障出现的早期，故障冲击特征较为微弱，依赖ITD单一的方法对信号进行处理，依然存留不少背景噪声，微弱故障的周期性冲击成分无法有效提取。最大相关峭度解卷积(maximum correlated kurtosis deconvolution， MCKD)是由MCDONALD等[11]提出的一种降噪方法，能够滤除信号中的大量背景噪声，使微弱故障信号的周期性冲击特征得到增强。该方法填补了最小熵解卷积[12](MED)只突出单个脉冲，而未考虑冲击成分周期性作用的不足。LI等[13]采用MCKD方法对信号进行去噪，去除了非冲击分量，并结合改进经验小波变换有效提取和增强了滚动轴承故障特征。祝小彦等[14]利用MCKD算法使冲击信号中的噪声进一步去除，实现了故障位置准确判断。尽管上述MCKD在故障诊断中取得了不错效果，但能针对算法中涉及的关键参数滤波器长度L和移位数M并未能针对给出确切的选择方法，主要靠主观经验选择，其准确性难以保证。

基于上述ITD在信号分解上的优势以及MCKD在滤波降噪方面的优势，本文提出了一种基于ITD与改进MCKD相结合的(ITD-IMCKD)方法应用到滚动轴承早期微弱故障诊断。信号经ITD进行预处理后，去除了无关成分干扰并保留了敏感故障冲击成分。同时，利用灰狼优化算法对MCKD中滤波器长度L和移位数M两个关键参数进行优选，确保了降噪效果的准确性，并清晰地提取了轴承故障频率信息。

1 构建ITD-IMCKD方法

1.1 ITD算法原理

ITD方法处理非线性非平稳信号可得到多个适当旋转分量(Proper Rotation Component，PRC)和一个残余趋势分量(Residual Trend Component，RTC)。假设故障信号为Xt，定义基线提取算子为L，分解过程表示为

Xt=LXt+(1-L)Xt=Lt+Ht,

(1)

式中:Lt为基线分量，Ht为适当旋转分量。

将一次分解后的高频旋转分量去掉，然后把基线分量信号作为下一次的待分解信号，其次将上述分解过程进行迭代，直到出现一个单调趋势分量信号。Xt的整个分解过程被定义为

(2)

式中:LXt为线性基线提取算子，HXt固有旋转分量提取算子，HLkXt为第k+1个旋转分量，LNXt为单调趋势分量。

1.2 MCKD算法原理

MCKD算法以相关峭度最大化为目标函数，通过迭代循环寻找最优滤波器，其目标函数为

(3)

式中:T为的周期数，M为移位数，N为信号样本数。

为求得使相关峭度最大时的最优滤波器，令

(4)

求解方程(4)便可得到一组最优滤波器系数组合，进而能恢复轴承故障信号中的冲击分量。

1.3 优选参数的IMCKD算法

MCKD算法的降噪效果主要受解卷积周期T、滤波器长度L和移位数M的影响。解卷积周期T可由理论理论计算得出(T=fs/f, 采样频率/故障频率)，然而参数L和M常根据人为主观选定。文献[15]中，滤波器长度L为[10，500]中的最优值，移位数M通常为[1，7]内的整数。MCKD算法中的L和M两参数是交互影响的，需要同时进行优选。

本文利用灰狼优化(Grey Wolf Optimizer，GWO)算法[16]对MCKD中的滤波器长度L和移位数M进行组合寻优。GWO算法是群体智能优化算法中的一种，具有调节参数省、鲁棒性强和搜索能力强等优势。GWO算法将狼群追踪、包围、追捕和攻击猎物等行为融合为算法流程，其中灰狼捕获的猎物即是最优结果。灰狼群体内部等级为四层，即α狼、β狼、δ狼、ω狼。

在GWO算法优化过程中，选择排列熵作为适应函数去衡量提取故障冲击特征的效果。排列熵值是度量时间序列复杂性和检测动力学突变的指标，信号排列熵值越大，信号中的高频故障冲击成分越多，信号的复杂度增加[17]。因此，本文将利用适应度函数最大排列熵值来评判是否得到最优结果。

对于振动信号时间序列{X(i)，i=1，2，…，N}，通过相空间重构得到矩阵X:

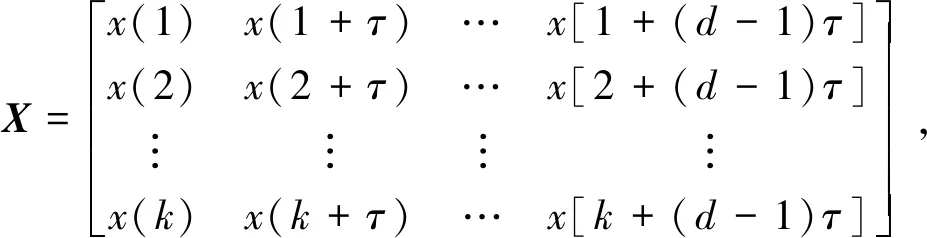
(5)

式中:τ是时间延迟，d是嵌入维数，x(k)是重构矩阵的第k行分量。对矩阵X的每个重构行分量进行升序排列，能够获得一组记号序列{j1，j2，…，jd}，可以看出共有d!种排列可能，得到的每一个记号序列的概率为P1，P2，…，Pk，因此可以计算出信号时间序列的归一化排列熵为

(6)

参数自适应优选步骤如下：

① 根据理论计算设定周期数T，滤波器长度L和移位数M的范围设定分别为[10，500]，[1，7]；

② 初始化GWO算法中的各项参数并确定适应度函数,本文中狼群数N设置为30，最大迭代次数设定为20，随机生成N个灰狼个体的位置；

③ 计算每个狼的初始适应度值，初始化α狼、β狼和δ狼位置；

④ 更新狼群当前位置和算法内部参数；

⑤ 计算更新后的每种灰狼的适应度值，重新确定α狼、β狼和δ狼的位置;

⑥ 当迭代次数达到最大，则结束，得到全局最优位置；若未达到，则转到步骤④继续迭代。

1.4 ITD-IMCKD方法诊断流程

综上所述，本文提出了一种结合ITD与改进MCKD的新方法，即ITD-IMCKD方法，避免了依赖人工经验选取参数的问题，并将所提方法用于轴承早期微弱故障诊断。其故障诊断流程如图1所示：

图1 故障诊断算法流程图

2 仿真分析

为了验证本文算法的有效性，将实际滚动轴承故障信号模型进行简化，建立了故障状态下滚动轴承振动信号的仿真模型：

(7)

(8)

式中：x(t)为是周期冲击信号，用于模拟轴承故障特征;n(t)为噪声信号;m为故障冲击个数;A0为位移常数;w(t)为单个冲击;T0为…；ξ为信号衰减因子;fn为系统共振频率。

对于仿真信号，设置采样频率为fs=12 KHz，采样点数为N=4 096，令A0=4，ξ=0.1，fn=4 000 Hz，故障冲击周期为T0=0.01 s，其故障特征频率为f=100 Hz。图2为含噪声的仿真信号s(t)的时域波形，由于大量背景噪声干扰，轴承故障冲击特征很难被观测到。仿真信号的包络谱如图3所示，图中仅能看到1～3倍频，且3倍频及其他多倍频依然淹没在噪声中，无法进行有效识别。

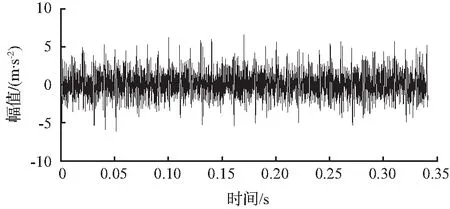
图2 加噪后的仿真信号时域波形

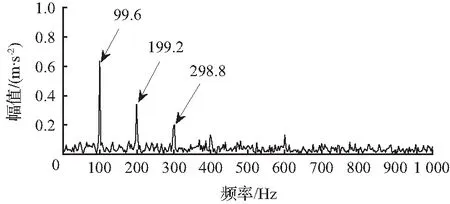
图3 仿真信号的包络谱

利用所提出的方法对轴承故障仿真信号进行ITD分解，计算分量的峭度和其与原信号的相关系数，结果见表1。由表1结果，PRC2和PRC3两分量峭度和相关系数都较大，PRC1峭度虽小但大于3且相关系数最大，而PRC4和PRC5分量相关系数较小，因此选择前三个分量进行重构。在此基础上，设置解卷积周期数T=fs/f=120,采用GWO算法对解卷积信号进行参数寻优，其寻优过程中排列熵随迭代次数的变化曲线如图4所示。在第6次迭代后，排列熵达到最大值，优选参数组合(L，M)为(342，2)。采用GWO改进的MCKD对重构信号进行滤波去噪 ，并对其进行包络谱分析，结果如图5所示。从包络谱中可以直观地观察出1～8倍频，整体故障信息体现较为全面。

表1 分量的峭度-相关系数

图4 仿真信号的GWO迭代关系曲线

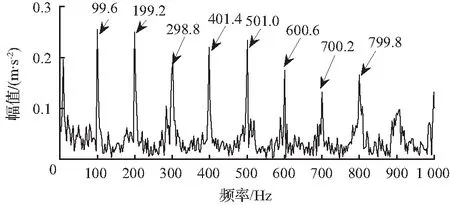
图5 经ITD-IMCKD后的包络谱

为了说明自适应优选参数的有效性，选用文献[15]中的经验参数值组合(300，5)对重构信号进行MCKD滤波降噪，并对降噪后信号进行包络谱分析，结果如图6所示。从包络谱中虽可得到1～6倍频处的故障信息，但7、8倍频未能有效提取，且整体的诊断效果相比本文方法较为微弱。

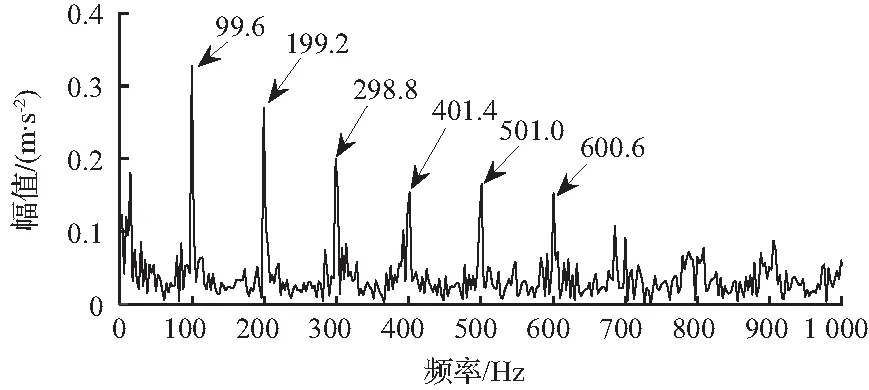
图6 经ITD-MCKD后的包络谱

通过仿真信号的分析，本文提出的ITD-IMCKD方法具有更明显的降噪效果，能突出故障冲击特征，使故障信息能够较为完整、清晰地保留。

3 实验验证

将所提出的轴承故障诊断方法应用到实际的轴承数据分析，选用美国凯斯西储大学轴承实验中心采集的数据进行验证。选取驱动端轴承故障数据，对应的轴承为6205-2RS JEM SKF深沟球轴承，其具体参数如表2所示。选择预制直径为0.177 8 mm的单点损伤模拟轴承早期微弱故障，实验中使用安装在电机本体驱动端的加速度传感器获取故障数据，采样频率为12 KHz，采样点数为4 096，电机转速为1 730 r/min(对应的转频fr=28.83 Hz)。根据表2，由理论计算可知，内圈故障频率fin=156.1 Hz，外圈故障频率fout=103.6 Hz。

表2 轴承结构参数

3.1 内圈故障分析

内圈故障信号的时域波形和频谱分别如图7、图8所示，从时域图中能够看出与故障冲击相关的成分被噪声完全掩盖，难以获得可靠的故障信息。从图8中同样可以看到信号的频谱图比较杂乱，依然很难提取到所需的故障信息，无法对故障进行准确诊断。

图7 内圈故障信号

图8 内圈故障信号的频谱

采用本文所提出的ITD-IMCKD方法，对采集到的轴承内圈故障信号进行ITD分解，根据峭度-相关系数，对敏感分量进行了重构，保留了感兴趣的冲击成分。为进一步提取内圈故障的微弱冲击特征，设置周期数T=fs/fin=77,运用GWO算法对MCKD参数进行寻优，排列熵在第12代后达到最大值，迭代曲线如图9所示，搜寻的优选参数组合(L，M)为(402，2)。将GWO算法改进的MCKD算法应用到内圈故障提取，图10为IMCKD对重构信号滤波降噪处理后的结果，可以看出故障冲击成分被明显突出增强。滤波后信号的包络谱如图11所示，因内圈故障点周围的载荷密度会随运转产生周期性变化，所以内圈早期故障会出现以转频为调制频率的幅值调制现象，包络谱中不仅准确地提取故障基频及其倍频成分，且基频及其倍频处的转频调制带也清晰可见，与理论计算基本相一致。这些调制频带为将来解释故障机理以及传递路径信息的识别提供基础。

为验证自适应优选参数的有效性，按照文献[15]中的经验值设定参数组合为(300，5)，采用此组合参数的MCKD算法对内圈重构信号进行降噪处理，图12为降噪后信号的包络谱。从图中虽也可看到1～6倍频，但基频及其倍频处的转频调制带相比本文方法未能有效提取，且该过程具有一定的随机性和偶然性。因此，利用GWO算法进行参数优选避免了人为主观因素的影响，实现了自适应分析。

作为对比，本文采用文献[18]所提ITD-MED方法进行诊断，其中MED算法主要受滤波器长度影响。因此，此处滤波器长度值L为402，其分析结果如图13所示。从图中可以看到故障提取效果较差，多倍频的故障特征依然被大量噪声信号包围，因此ITD-MED方法不利于早期微弱故障诊断。

图9 内圈故障信号的GWO迭代关系曲线

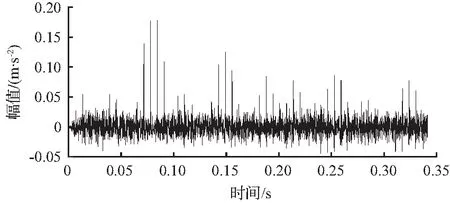
图10 内圈重构信号经IMCKD后的时域波形

图11 内圈故障信号经ITD-IMCKD后的包络谱

图12 内圈故障信号经ITD-MCKD后的包络谱

图13 内圈故障信号经ITD-MED后的包络谱

3.2 外圈故障分析

外圈故障信号的时域波形和频谱分别如图14、图15所示，从时域图和频谱图也很难提取到所需的故障信息，无法对故障进行准确诊断。

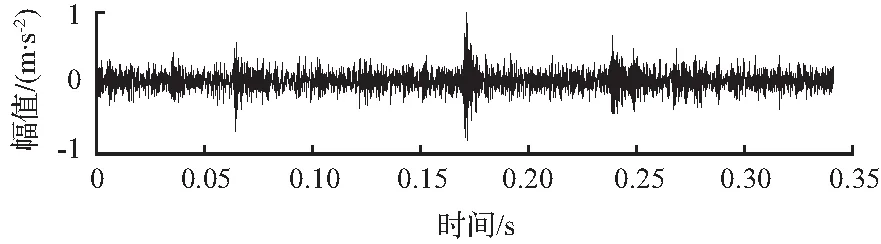
图14 外圈故障信号

图15 外圈故障信号的频谱

对采集的轴承外圈故障信号利用所提出的ITD-IMCKD方法进行特征提取，其中周期数为T=fs/fout=116,通过GWO算法对MCKD参数进行寻优，排列熵在第11代后达到最大值，迭代曲线如图16所示，搜寻的优选参数组合(L，M)为(186，5)。经IMCKD对重构信号滤波降噪处理，结果如图17所示，可以看出微弱冲击特征被增强。滤波后信号的包络谱如图18所示，从图中可以清晰地看到整体的外圈故障成分被提取出来，与理论计算基本一致。

图16 外圈故障信号的GWO迭代关系曲线

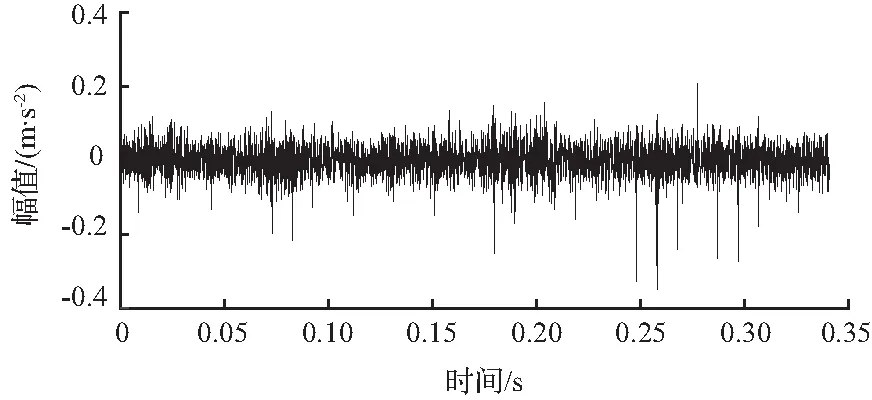
图17 外圈重构信号经IMCKD后的时域波形

为验证自适应优选参数对轴承外圈故障特征提取的有效性，以文献[15]中经验值参数组合(100，5)对外圈重构信号进行MCKD降噪处理，图19为降噪后信号的包络谱。从图中虽然可以看到1～6倍频，但3～4倍频提取效果较差，且6倍频后的成分依然淹没在噪声中，未能提取出来。

图18 外圈故障信号经ITD-IMCKD后的包络谱

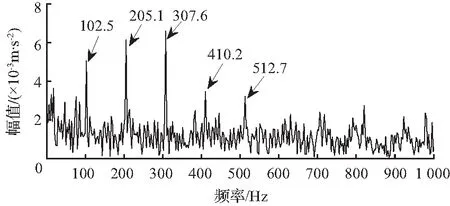
图19 外圈故障信号经ITD-MCKD后的包络谱

作为对比，对ITD处理后的外圈重构信号也进行MED算法滤波，滤波器长度L设置为186，其结果如图20所示。从图中仅仅可以观察到1～3倍频，无法提取更多有用信息。

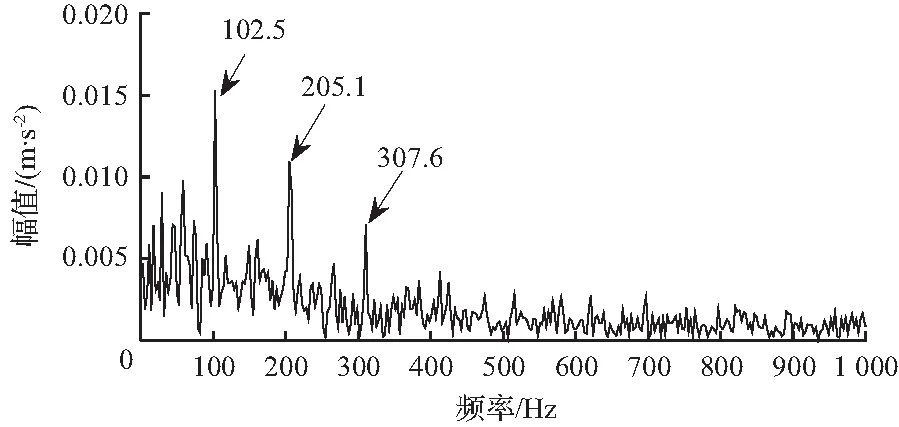
图20 外圈故障信号经ITD-MED后的包络谱

4 结论

仿真和实验数据分析结果表明，本文所提出的基于ITD与IMCKD相结合的方法可以准确地从含有大量噪声的轴承故障信号中提取微弱故障特征，表明其在滚动轴承早期故障诊断中的有效性，并得到了如下结论：

① 针对人工经验设定MCKD算法中滤波器长度L和移位数M会对降噪效果产生不确定性的问题，利用GWO算法以解卷积后信号的排列熵为优化目标，依据排列熵越大，信号中的高频冲击成分越多，得到了MCKD参数的最优选择。

② 利用峭度-相关系数越大，冲击成分越多的准则对ITD分解后的敏感分量进行了筛选并重构信号，去除了无关噪声成分的干扰，结合GWO算法改进的MCKD算法进一步滤波降噪，能有效地抑制噪声干扰并清晰有效地提取出轴承的基频及其多倍频故障信息。

③ 在进行轴承早期微弱故障诊断的仿真和实验分析中，本文所提出的ITD-IMCKD方法相比于一些传统方法，如ITD-MCKD、ITD-MED等方法，可以提取更多的多倍频信息且具有更好的诊断效果。