联通核心知识，促进迁移创生

张苾菁

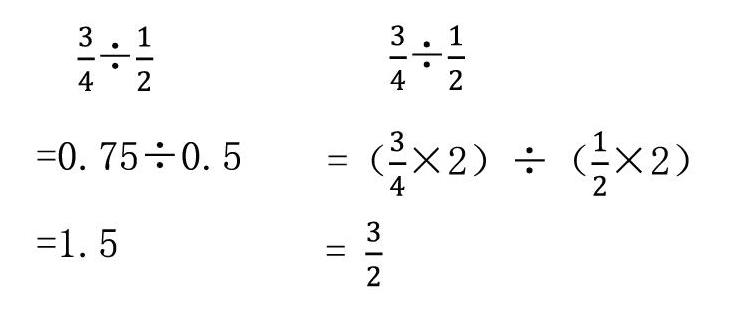
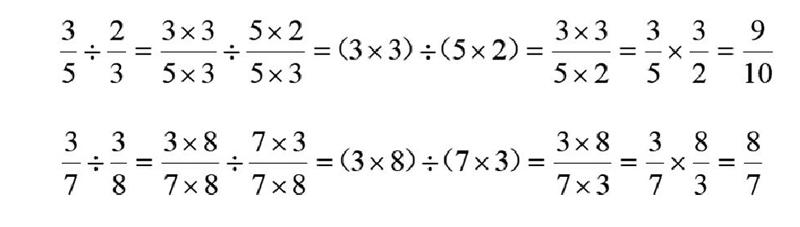
当学生遇到一个新的问题时，将已有的经验与未知的问题间建立一定关联，从而打开新知与经验之间的通道，建构属于自己的知识结构，这个过程就是迁移。围绕小学运算领域的内容，我们不难发现，几乎所有的计算都可以用迁移来解决。如何让学生基于一定的情境，通过自主探索，充分运用迁移的认知规律在理解算理、创新算法？笔者以分数除法为例来谈几点思考。

一、善用情境——经验助迁移

分数除法若单独出现，学生或许会感到无从下手，但是，如果能结合具体的情境，伴随着生活经验的支撑，便能很好地理解。比如，一般来说，分数除法教学的第一个例子都是分数除以整数。苏教版教材是通过将升饮料平均分给2个小朋友，每人喝了升的来呈现。类似这样的算式，分数除以整数可以转化为分数乘几分之一，这个转化主要依赖平均分在其中所发挥的作用。情境的运用能起到很好的直观支持，学生通过分一分、画一画，可以将其中的道理与之前解决问题的经验很好地联系起来，迁移自然而然发生。

然而，遇到类似4÷、÷整数除以分数或者分数除以分数的情况，等分除的意义很难直接迁移，用来解释其算理，这时包含除的意义就便于学生理解。苏教版教材选用的情境是4个橙子从每人分2个、每人分1个、每人分个，逐步从整数除以分数过渡迁移，因为1个橙子可以分给2个人，那么4个橙子就可以分给8个人，所以4÷=4×2，也比较容易解释算理，便于归纳计算方法。

然而，对于同一个算式而言，它事实上可以代表不同的模型，以÷为例来看，至少可以有以下几种情况。

包含模型：里有几个？

等分模型：求一个数，使它的正好是。

面积模型：一个长方形的面积是，长是，宽是多少？

当然，我们也可以把同样的算式置于同一个情境素材之中，以更加贴近儿童的生活实际，让学生在相似的情境中体悟其中的不同。

1.桌上有两包巧克力，德芙巧克力重千克，金帝巧克力重千克，德芙巧克力的重量是金帝巧克力重量的几倍？

2.桌上有德芙巧克力千克，小明想把它每千克装一袋，小明一共可以装几袋？

3.桌上有德芙巧克力千克，正好是小明家里所有巧克力的，小明家里一共有多少巧克力？

……

教师需要情境设计能力，只有教师的视野宽了，学生对分数除法意义的理解才会透彻和全面，应用起来才会得心应手。同一知识只有在不同的情境下得到充分运用，学生才能领会其最核心的要义，知识的主动迁移才能得以实现。

二、关注联通——明理促迁移

要让学生主动迁移，了解学生已有知识是非常重要的。某一个新知识究竟和哪些知识有关？孰近孰远？谁是最临近的知识点，谁又是最核心的知识点？它和曾经学过的知識有什么相同，又有什么不同？这是需要在比较中进行沟通，并明晰其本质的。

分数除法的算理究竟是什么？学生理解算理依赖的基础又是什么？能不能把算法学习建立在算理理解的基础上，和以往的整数的计算本质联通起来？事实上，确实是可以的。如果我们把计数单位（分数单位）和运算的意义作为核心去思考，也可以发现，计算教学的中枢神经是计数单位，分数运算就是分数单位相同前提下分子的运算，即整数的运算。这样就把整数运算与分数运算联通起来，为解释分数除法的算理提供了依据。教学按如下环节进行。

【环节1】

师：÷，你会怎么算？

生1：我准备把分子除以分子，分母除以分母。

师：你是怎么想到用这个办法的？

生1：因为除法是乘法的逆运算，既然分数乘法的法则是分子乘以分子、分母乘以分母，那么由此推理分数除法的法则是分母除以分母，分子除以分子，结果是。

生2：我还可以用转化的办法。

师：具体说一说。

生2：可以转化为小数0.75，可以转化为0.5，0.75÷0.5=1.5。

生3：我也是转化，但是和上面的同学不一样。可以根据商不变规律把他们都同时乘2，这样原来的算式就是除以1了，商还是。

师：非常好，这两位同学都想到用转化的方法把暂时不能解决的新问题变成可以用以前的知识解决的问题。我们可以把刚才同学们的一些想法用递等式一步一步写下来。

利用已有经验，将简单的除数是分数的除法进行转化，从而得出计算结果，对于六年级的学生而言，难度不是很大。但要在一般意义上进行推广，形成对计算方法更清晰的认识，并对计算的本质有更深的感悟，还需要进一步联系算理进行深入比较和联结。

【环节2】

师：我发现有一位同学用了这样的办法，你们觉得有道理吗？

÷ =÷=3÷2=。

生1：他先把两个分数通分了。

生2：通分以后就只剩分子相除了，这样简单。

师：但是这样做，有道理吗？

生3：这道题就是求里有几个，也就是3个，也就是2个，它们的分数单位是一样的，都是，就相当于求3里面有几个2。

师：你的意思是说，分数单位相同，只要分子相除就可以了，对吗？

生3：是的。

师：那如果反过来，÷，该怎么理解？

生4：÷，就是用÷，就是求“2个”里有几个“3个”。

师：这样说有些拗口，简单地说，因为分数单位相同，我们就可以理解成“求2个是3个的几分之几”，也就是求2是3的几分之几。

师：和同桌再用这样的方法计算两道分数除以分数的题目，看看用这样方法是否行得通（出示和 ）。

生1：我们算的是 。

生2：我们算的是 。

师：老师把你们的计算过程稍作补充和改动，仔细观察，你发现了什么？你能说出每一步的变换前后的联系和依据吗？

生：通分以后，分数单位相同，我们直接将分子相除就可以了。

师：这样原来分数的除法转化为整数的除法，根据分数与除法的关系我们对算式稍作整理就会发现。

生：我发现原来的除法最后变成了乘法，和我们前两节课学的分数除以整数的方法是一样的！

师：比较原来的除法算式和最后的乘法式子，有什么相同和不同？

生：第一个数没有变，第二个数变成了原来的倒数，而且中间的符号是乘号了。

师：所以，分数除以分数，也可以用分数除以整数和整数除以分数的方法，转化成用被除数乘上除数的倒数，这里的道理你明白了吗？是哪个重要的知识在帮助我们实现这样的转化呢？

……

用通分的办法来帮助学生勾连分数加减法和乘除法的关系，不失为一种有益尝试。在学生以往大量的学习经验中，对“计算的本质就是相同计数单位的个数相加减”有比较深刻的体会，而在分数的乘除法教学中，这样一种内在的联系似乎被忽略或者说是被遮蔽了。学生探索分数除以分数的过程往往是另起炉灶，或转化为小数，或用“商不变性质”展开，突出了形式上的“颠倒相乘”而忽视了用计数单位（分数单位）去解释这件事情，不利于对运算整体算理与算法的沟通和联系。在分数单位相同的前提下，分数的运算转化为分子的运算，好处在于将分数的运算与整数的运算直接建立起联系，不需要增加新的知识和技能，就可以直接用以往的知识进行迁移，并推广到更大范围内的除法运算。事实上，任意一个数除以一个不为零的数，都可以转化为将这个数乘以除数的倒数。这样的算理形成过程更有基础，也更有利于学生温故知新。同样的算理对于分数乘法也适用，法则中，分母乘分母的过程就是在理解分数意义的前提下，通过两次平均分，统一计数单位的过程。

三、整体关照——结构助迁移

类似这样的数学课堂，我们特别需要教师有整体建构的眼光，帮助学生建立起知识前后的联系，比如，在学习分数除法的时候，学生会想到、用到哪些知识呢？在这些知识中，哪些是最核心的东西呢？

任何运算最终都是在研究“在什么条件下，按照什么关系，用什么计算（为什么能够和需要这样算），甚至发明什么计算”。在了解算理的内核以后，我们在教学中就不会被外在的变化所迷惑，也不用被众多的法则所束缚，而是能够抓住主线，凸显本质。教师需要做的便是当学生的经验知识积累到一定程度时，提供典型的例子引導学生进行综合、整理，使之条理化。从这个角度看，学习是一个连续的过程，前面的知识支持新的知识，新知识又加强和深化原先的知识。

抓住核心内容，在联系中学习，在迁移中创生，进而完善认知结构，实现从知识到智慧的生长，这是教育者需要不断在实践中探索的重大课题。

（作者单位：江苏省苏州市善耕教育集团）

责任编辑：李莎

lis@zgjsz.cn