基于L0稀疏先验的运动模糊标签图像盲复原
柳宁 赵焕明 李德平 王高
(暨南大学 信息科学技术学院∥机器人智能技术研究院,广东 广州 510632)
家电在人们的生活中有着举足轻重的地位,因此其质量检测就显得弥足重要。家电质量检测包括外观检测、尺寸检测等。外观检测主要检测产品的表面缺陷,最常见的表面缺陷包括表面形状缺陷、表面装配缺陷和表面印刷缺陷等。在传统的家电生产制造车间里,家电的质量检测往往由工人完成。由于工人长时间工作容易疲劳,以及检测指标的复杂性,质检过程中容易出现错检漏检的现象。应用机器视觉技术实现质量检测自动化,是工业流水线智能化的趋势。标签质量检测是一项重要的家电质量检测内容,属于外观检测中的表面印刷缺陷检测。将检测相机固定在工业机器人的末端,并与工业流水线上运动的家电进行随动检测,可以提高质量检测的效率和准确率,这种采用机器人和相机进行标签质量检测的方式在国内尚未见有先例。
图1描述了一种典型的家电标签质量检测场景,主要由机器人控制模块、视觉检测模块、编码器测速模块和传送带运动模块组成。视觉检测模块由传送带的顶部相机和机器人末端的相机组成。家电随运动的传送带进入固定于顶部的相机的视野内,顶部相机拍摄家电的顶部并通过图像处理和坐标系转换得到家电在传送带的实际位置,并把这个位置发送给机器人控制模块,机器人控制模块同时收到编码器测速模块检测到的传送带的速度。在理想情况下,机器人开始运动并与家电保持相对静止,根据规划好的运动轨迹,定点拍摄家电机体上的标签,并在后台做质量检测处理,达到在不停机的前提下自动检测的目的。

图1 标签质量检测场景图
然而在实际的作业现场中,机器人末端相机拍摄得到的图像会出现运动模糊的现象,影响后续的标签检测处理,其原因主要有以下3点:①速度误差——由编码器反馈得到的传送带速度与真实的传送带速度无法完全一致,导致机器人无法与家电保持相对静止;②标定误差——机器人坐标系和传送带坐标系在方向上不是绝对的平行,通过工件坐标系标定,可以部分修正这个角度上的偏差,但无法完全消除误差,导致机器人运动的方向与家电运动的方向无法保持一致;③振动误差——由于机器人运动轨迹规划设计不当、机器人运动学和动力学模型不够精确,或者机器人本身存在结构缺陷等原因,机器人的运动轨迹不光滑,机器人末端在运动过程中会出现轻微的抖动,从而使得拍摄的图像出现运动模糊的现象。
图2是工业现场拍摄的实际作业图像,图3是相机拍摄到的实际标签图像及处理后的标签图像。如图3(a)所示,实际拍摄到的标签图像有运动模糊的退化现象,影响后续的标签检测结果。因此对运动模糊图像进行复原有着迫切的实际需求。

图2 工业现场图
在得到现场的标签图像后,需要定位到图像中的标签,并做仿射变换和白平衡,消除畸变和偏色等的影响,得到如图3(b)所示的标签图像,再对模糊图像做复原处理。

图3 运动模糊的现场标签图像和处理后的标签图像
如果模糊内核是空间不变的,则可以将模糊内核视为统一的模糊内核。图像的模糊过程可以建模成卷积操作[1- 3],如下式:
B=L⊗K+n
(1)
式中,B、L、K和n分别表示运动模糊图像、复原图像、模糊核和噪声干扰,⊗代表卷积操作。运动模糊图像复原的目的是从式(1)得到复原图像L和模糊核K,这显然是个高度病态的问题,因为不同的L和K的组合都可以得到B。
从未知的模糊核K和已知的模糊图像B中逆卷积得到复原图像L,这一过程称为图像盲复原[4]。针对这一问题,学者们提出了很多方法,主要有两类:贝叶斯方法和正则化方法。贝叶斯方法的思想是充分利用图像参数的先验知识,把图像参数的先验概率转换到图像的后验概率,在贝叶斯框架下通过一系列最优化方法得到模糊核和复原图像。Fergus等[5]发现自然图像的梯度分布存在重尾效应,据此提出了混合高斯模型作为图像先验,并结合模糊核具有稀疏性这一特点,在最大后验概率(MAP)框架下采用变分贝叶斯方法求解得到模糊核;Shan等[6]发现用高斯混合模型作为图像先验时计算速度慢,因此提出用两个分段的连续函数去拟合自然图像的梯度分布,并结合图像的局部区域像素分布具有光滑性这一特点来实现去模糊;Cho等[7]提出一个多尺度架构,基于图像梯度(而不是像素值)实现图像的去模糊,并用双边滤波器和冲击滤波器抑制图像噪声,将复杂的卷积操作转换到频率域来加速计算过程。运动模糊图像的复原是一个高度病态的问题,为了解决这一不适问题,正则化方法通过在能量函数方程中添加正则化项作为方程的约束项,从而将其转换成适定问题。Krishnan等[8]提出L1/L2范数作为标准化稀疏先验的正则项,这种正则化对清晰图像有利;Pan等[9]观察文本图像后发现,文本图像的像素分布和梯度分布都呈现稀疏性,因此提出了基于像素分布和梯度分布的L0正则化约束,并在多尺度框架下迭代求解得到模糊核和复原图像,在文本图像去模糊方面取得了很好的效果;Chen等[10]将经过模糊处理的局部图像块的最大梯度值明显减小这一特性加入到传统的基于稀疏先验的能量函数中,提出了一种基于先验局部最大梯度的盲去模糊架构,并从数学上和实验上证明了方法的有效性。
针对运动模糊标签图像复原这一问题,文中受文献[9]的启发,通过观察清晰标签图像的像素直方图和水平方向梯度直方图(见图4),发现标签图像的像素分布与清晰文本图像的并不一致——文本图像的文字和背景区域都有着恒定的像素,而标签图像在像素分布上要复杂很多。L0正则化的值是图像像素中非零值的个数,从清晰标签图像的像素直方图来看,像素L0正则化的值恒等于常数[11],即‖x‖0≡C。
所以,通过分析可知,图像像素的L0正则化项不适用于标签图像的去模糊。观察图4(c)可发现,清晰标签图像的梯度直方图中,零值的梯度值占绝大部分,梯度分布呈现稀疏性,因此可以用L0正则化稀疏先验建模图像的梯度分布。根据这一

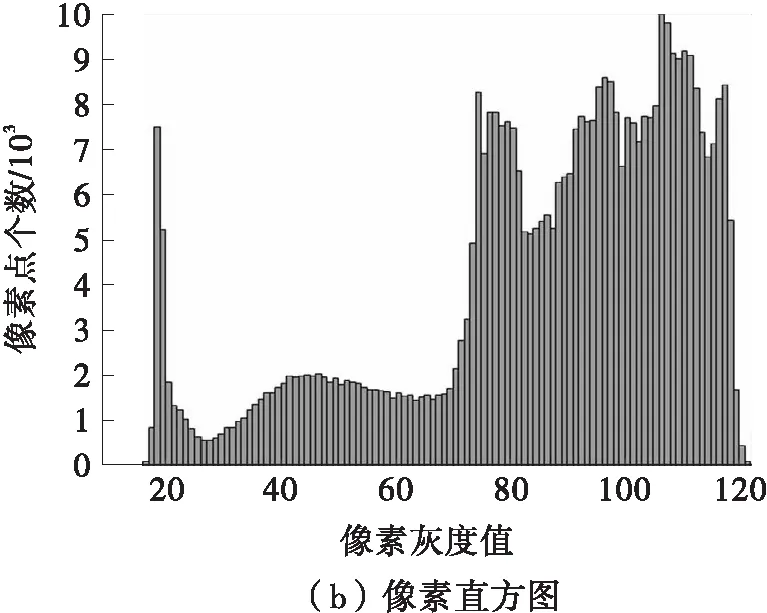

图4 清晰标签图像及相应的像素和梯度直方图
特点,将L0范数引入去模糊模型中,构建运动模糊标签图像复原的能量函数模型如下:
(2)
式中:‖L⊗K-B‖2表示能量函数的约束项,用来保证复原图像和模糊图像之间的误差最小;‖L‖0是对原始图像梯度的L0正则化约束,‖K‖2表示能量函数的惩罚项,防止最优解过拟合;α和β分别表示相对应的加权系数。
1 算法框架
式(2)的求解可以拆解为两个子问题的求解,如下式:
(3)
(4)
1.1 固定K估计L
由于L0范数是高度非凸的问题,直接通过优化式(3)求解L是很困难的。考虑到这个特性,可以通过半二次分裂法[12]求解。引入辅助变量u=(uh;uv)→L,将目标函数(3)重写为
(5)
式中,α是式(2)定义的系数,γ是相应的加权系数。当γ趋近于∞时,式(5)的解接近式(3)的解。式(5)的求解是通过固定其他变量,分别独立地最小化L和u来实现的[9]。
变量u的值一开始被初始化为0,所以在每次迭代中,L的解可通过下式求得:
(6)
式(6)是最小二乘最小化问题,其封闭解可以通过快速傅里叶变换实现快速求解[7],其解为
L=
(7)

当给定L时,可以通过下式求解u:
(8)
式(8)是一个逐像素的最小化问题,参考文献[8]的求解方法,可得
(9)
式(5)的求解步骤(算法1)可以归纳如下:
输入:模糊图像B和模糊核K;
L←B,γ←2α;
do:
使用式(9)得到解u;
使用式(7)得到解L;
γ←2γ;
whileγ>γmax。
输出:复原图像中间值L。
1.2 固定L估计K
当给定L时,式(4)跟式(6)一样是最小二乘最小化问题,其封闭解可以通过快速傅里叶变换求解。根据文献[7],直接基于图像的像素值求解式(4)不是一个快速方法,所以将式(4)转换到梯度空间去估计K,即
(10)
通过快速傅里叶变换可以得到式(10)的解为
(11)
式中,
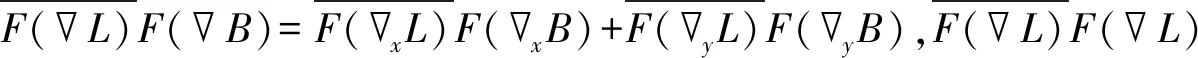
在得到模糊核K后,将K中的负值设为0,并把K归一化,使得K的每个元素的值的总和为1。
式(4)的求解(算法2)可以归纳如下:
输入:模糊图像B,最底层模糊核K;
do:
使用算法1得到解L;
使用式(11)得到K;
α←max{α/1.1,e-4};
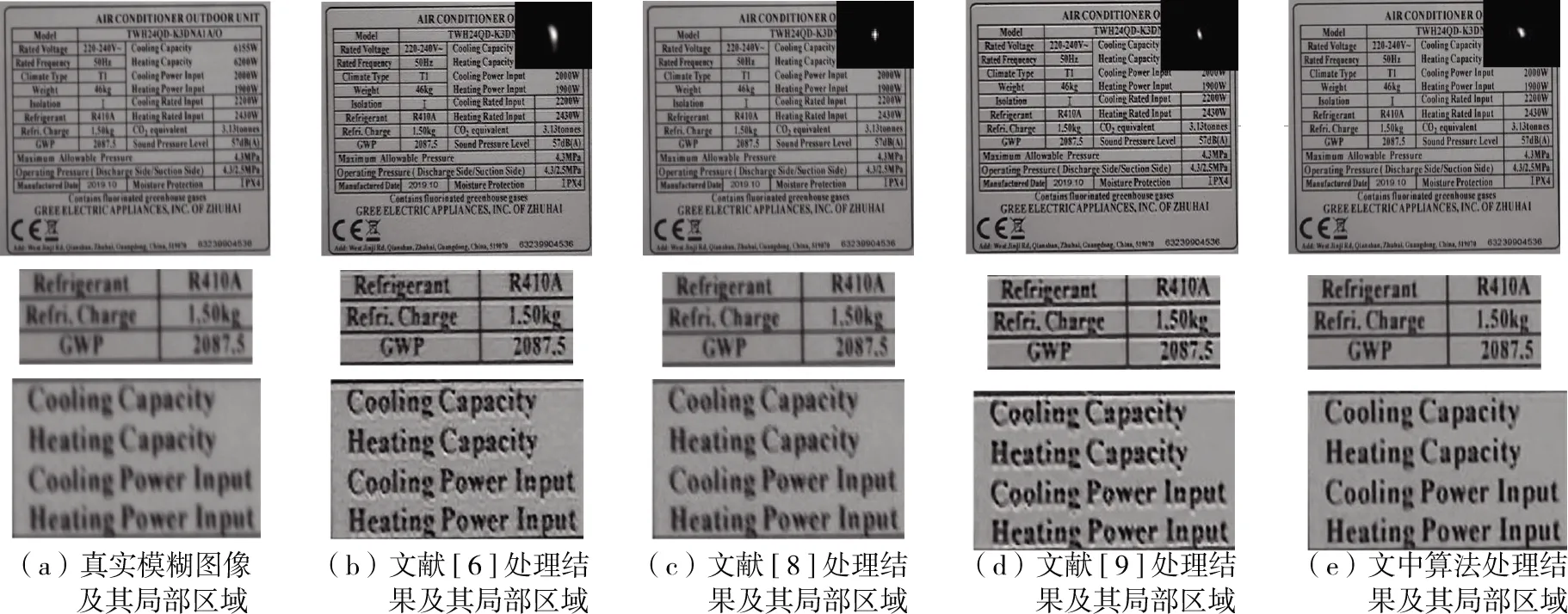
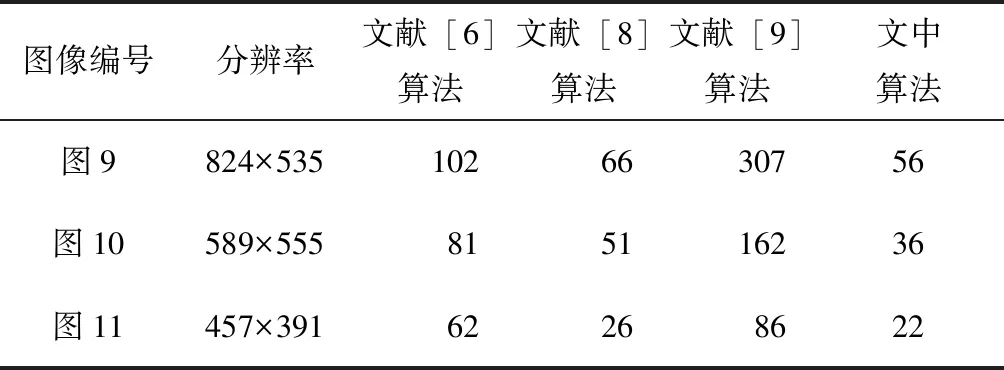
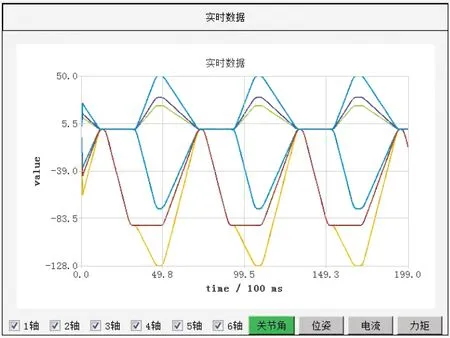
whilei 输出:模糊核K,复原图像L。 由于噪声的干扰和高频信息的缺失,在图像复原的过程中,图像的边缘会出现振铃现象[13]。为了有效降低振铃效应对图像复原质量的影响,在每次估计图像的迭代计算过程中,使用双边滤波器[14]对估计图像进行滤波处理。双边滤波器利用了像素点邻域内的空间邻近度信息和亮度相似信息,在有效降低图像噪声的同时,可以保持图像的边缘信息,即图像的高频信息,有利于模糊核的估计,并抑制振铃效应。双边滤波器的公式可以表示为 (12) 式中,d(·)函数表示邻域点j和中心点i的空间相近的程度,l(·)函数表示i点和j点之间的亮度接近程度,b表示处理的图像,ω表示以i为中心的区域,γi为归一化因子。 文中实验在Intel Core(TM)i5- 7300HQ、2.5 GHz处理器、64位Win10系统、8G内存的PC机上用Matlab2017b进行测试。工业相机为映美精DMK 33GX174全局相机。 实验的第1部分将测试文中算法在由运动模糊核生成的模糊图像上的效果,将其与其他文献中的算法作比较,并用峰值信噪比PSNR作为合成模糊图像复原的评价标准;实验的第2部分是测试文中算法在现实世界采集到的模糊图像上的效果,同样也会与其他文献中的算法作比较。在所有的实验中,算法使用的参数数值为:α=0.004,β=2。所有其他文献的算法都来自于文献作者的网站,并且参数都采用默认值。 由式(2)可知,α是正则化项‖L‖0的加权系数,而‖L‖0是能量函数(2)中一项重要的约束项,α的取值会影响‖L‖0在能量函数(2)中所占的权重,从而影响图像复原的质量和算法的运行效率。 图5所示为α值对PSNR和运行时间的影响。α取值在10-7~10-2之间,其步长是10-5。 图5 α值对PSNR和运行时间的影响 峰值信噪比PSNR是一个用于评价图像质量的客观指标,单位是dB,定义为 (13) 式中,I表示复原的图像,I0表示原始的图像。对于PSNR来说,其值越高,图像复原的效果越好。 分析图5,PSNR和运行时间在区间1波动较为明显;在区间2,运行时间趋于稳定,PSNR则下降明显,图像复原的效果差;在区间3,PSNR和运行时间趋于稳定,没有明显的波动;在区间4,PSNR和运行时间波动明显,有一小段区域的图像复原效果差。因此算法选择区间3内的α值,为0.004。 首先测试算法模型在合成的运动模糊图像上的效果,并与文献[6,8- 9]中的算法作比较。文献[6]算法是贝叶斯方法;文献[8- 9]和文中算法都是正则化方法,文献[8]将图像的L1/L2范数作为正则项,文献[9]将图像强度的L0范数和图像梯度的L0范数作为正则项,而文中算法采用图像梯度的L0范数作为正则项。 运动模糊核包括两个部分:沿顺时针旋转的运动模糊角度θ和运动模糊长度l。 图6(b)的运动模糊核为K1:(l,θ)=(10,5),图7(b)的运动模糊核为K2:(l,θ)=(5,10),图8(b)的运动模糊核为K2:(l,θ)=(7,7)。 图6 合成模糊图像1的算法处理结果比较 图7 合成模糊图像2的算法处理结果比较 图8 合成模糊图像3的算法处理结果比较 从实验结果看,文献[9]的算法无法很好地恢复图像的清晰度,复原的图像带有严重的振铃效应,且运行的效率最慢,远大于文中算法。从表1可知,文献[9]算法的PSNR最小,因此可知像素分布的稀疏先验约束不利于模糊标签图像的复原。而文中算法的处理效果明显好于其他方法,并且从表2所示运行时间上看,文中算法的效率是最高的。 表1 合成模糊图像实验的PSNR 表2 合成模糊图像实验的运行时间 如表1,文中算法的平均PSNR为35.913 dB,高于其他3种算法的平均值。 图9(a)是一张实际拍摄到的运动模糊标签图像,在标签类别中属于警告类标签,一般由图标和文字说明组成。观察图9(a)的局部区域,由于运动模糊,图像的文字难以识别。和其他方法相比,图9(e)表明文中算法在抑制振铃效应的同时实现了图像去模糊,而文献[9]算法无法得到清晰的图像边缘。 图10(a)属于铭牌类标签。观察图10(a)的局部区域,图中的英文字符和数字的边缘已经被模糊,观察局部图像,文献[9]算法虽然能恢复出比较清晰的边缘,但是在边缘周围同时出现了振铃效应;而文中算法既可以恢复出清晰的效果,也没有明显的振铃效应。 图11(a)属于带有条形码的标签,保证条形码和下面的数字的清晰度是至关重要的。观察实验结果,发现4种算法都能恢复出图像清晰的边缘,但文中算法在抑制振铃效应方面效果更好。 时间指标是衡量一个方法是否优越的重要指标,表3给出了文献[6,8- 9]和文中算法运行时间的比较。可以看出,文中算法的运行效率最高,而文献[9]算法的运行效率最低。综合表2和表3,文中算法的平均运行速度比文献[6]算法快了53.45%,比文献[8]算法快了17.30%,比文献[9]算法快了80.52%。 图9 真实模糊图像1的算法处理结果比较 图10 真实模糊图像2的算法处理结果比较 图11 真实模糊图像3的算法处理结果比较 图12所示为机器人控制系统程序截屏,可以手动控制机器人运动,也可以发送运动指令控制机器人运动。文中实验是通过与机器人控制系统程序建立通信,并发送运动指令来控制机器人运动。 表3 真实模糊图像实验的运行时间 图12 机器人控制程序截屏 图13所示为机器人各关节角在运动过程中的实时数据截屏。可以看出,机器人在运动过程中,各关节轴的运动是均匀的,因此机器人的运动不是造成机器人末端抖动和图像运动模糊的原因。 图13 关节角运动实时数据截屏 图14是标签检测软件界面。标签检测算法对标签设计稿进行模板特征提取,并存入数据库中。在实际的检测过程中,检测软件得到标签图像后,做相应的预处理,并采用文中算法对图像进行去模糊,提取去模糊后的图像的特征,并与数据库中的特征作对比,显示的检测结果为“通过”。 图14 标签检测软件界面 为解决运动相机拍摄的标签图像的模糊问题,文中提出一种基于正则化方法的盲复原算法。根据标签图像梯度直方图的稀疏性,将图像梯度的L0稀疏先验作为约束项,提出高精度的优化函数模型。采用半二次分裂法对L0最小化问题进行求解,并用快速傅里叶变换显著提高了运算速度。在模糊核估计阶段,采用图像金字塔的多尺度方法对算法进行优化,避免出现算法在迭代优化过程中陷入局部最优的问题;在图像估计阶段,采用双边滤波器对估计图像做滤波处理,有效抑制了振铃效应。选取合成的模糊标签图像和实际拍摄的模糊标签图像进行实验,并将实验结果与其他盲复原算法的结果进行比较,发现文中提出的算法在恢复图像清晰度的同时,能有效地抑制图像边缘的振铃效应,保留完整且清晰的边缘信息,并将运算速度提高80.52%,对模糊标签图像有着良好的复原效果。1.3 多尺度优化
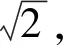
1.4 抑制振铃效应
2 实验设计及结果分析
2.1 实验条件
2.2 能量函数中的α值

2.3 合成的模糊图像






2.4 现实世界的模糊图像




3 结论

