泵阀并联电液位置伺服系统的智能控制方法
汪成文 郭新平 张震阳 刘华
(1.太原理工大学 机械与运载工程学院,山西 太原 030024;2.太原理工大学 新型传感器与智能控制教育部重点实验室,山西 太原 030024;3.浙江大学 流体动力与机电系统国家重点实验室,浙江 杭州 310058)
电液伺服系统因其功率密度高和响应速度快等优点,在航空航天、国防军事和民用工业等领域都有着广泛的应用,如飞机的作动系统、雷达驱动装置、导弹发射系统、液压机器人和注塑机等[1- 2]。电液伺服系统按控制元件的不同可以分为泵控系统、阀控系统和泵阀复合系统,其中泵阀复合系统又可以分为泵阀串联系统和泵阀并联系统,文中研究对象为泵阀并联系统。泵阀并联系统由泵控子系统和阀控子系统两部分组成,两个子系统是并联关系,进入执行机构的总流量由泵控子系统和阀控子系统共同提供[3]。由于泵阀并联系统兼具泵控系统能效高和阀控系统性能好的优点,近年来逐渐引起了一些学者的关注[4- 6]。
汪首坤等[4]针对泵阀并联系统的动态跟踪控制,提出了一种泵控回路采取固定PID控制、阀控回路采取迭代学习控制的复合控制策略,仿真结果表明该控制策略能提高系统的跟踪精度。Ding等[7- 9]提出了一种阀-泵并联变结构控制的液压马达调速系统,首次建立了阀-泵权重比的概念,详细研究了阀控回路与泵控回路的流量分配对系统控制特性的影响,通过改变不同调速阶段的阀-泵权重比,使得系统可以实现低速平稳的快速启停、负载干扰的快速调节,获得全程高效率的综合性能。Li等[10- 11]针对大直径泥水盾构推进系统提出了一种比例变量泵、比例伺服阀并联控制的推进技术,建立了该泵阀并联推进系统的非线性数学模型,并且利用反步法设计了基于干扰观测器的泵阀并联压力控制器,仿真和实验表明该控制策略可以减少系统能耗,提高系统的压力控制精度。付永领等[12]研究了电机泵阀并联的飞机作动系统的能量效率问题,提出了一种分级压力控制方法,仿真结果显示该方法可以显著降低系统发热,提高系统效率。
泵阀并联电液伺服系统虽然结合了泵控系统和阀控系统的优点,但同样具有液压系统固有的参数不确定性和外负载干扰等问题,这些问题给系统的高性能控制带来了挑战。目前针对泵阀并联系统的控制方法大多仍为传统的PID控制,然而,基于经典控制理论的PID控制已经难以满足此类非线性系统的高性能控制要求。有鉴于此,文中开展了泵阀并联系统的智能控制方法研究,以期提高系统的控制性能。
1 泵阀并联系统的工作原理
文中研究的泵阀并联电液位置伺服系统由1个泵控子系统和1个阀控子系统构成,其原理如图1所示。并联系统的具体工作过程如下。

1—伺服电机;2—转速传感器;3—双向定量泵;4—油箱;5—液控单向阀;6—溢流阀;7—液压缸;8—位移传感器;9—负载;10—阀控子系统位置控制器;11—伺服阀;12—恒压油源;13—转速指令规划器;14—泵控子系统转速控制器
(1)泵控子系统的转速控制

(2)阀控子系统的位置控制
阀控子系统位置控制器10的输入端接收位置指令和位移传感器8反馈回来的实际位置,并基于相应的控制算法生成控制信号,通过控制伺服阀11的阀芯位移实现对液压缸7的位置闭环控制。
2 控制器的设计
由于泵阀并联电液位置伺服系统的控制涉及到泵控子系统的转速控制和阀控子系统的位置控制,因此分别为两个子系统设计了控制器。其中:为泵控子系统设计了单神经元PID控制器,该控制器可以实现PID参数的自适应,即通过神经元的学习自动为系统找到一组合适的PID参数;为阀控子系统设计了RBF神经网络滑模控制器,采用RBF神经网络来逼近阀控子系统数学模型中的未知项,实现了参数未知情况下阀控子系统的位置控制,有效地解决了阀控子系统的参数不确定性问题。
2.1 泵控子系统的单神经元PID控制
传统PID控制器的参数调整困难,很难找到一组各种工况下控制性能都好的参数,且控制器的鲁棒性较差。为此,文中采用一种将神经元与PID控制相结合的方法来实现泵控子系统的转速控制,该单神经元PID控制器可以实现PID参数的自适应,即通过有监督的Hebb学习规则来找到一组合适的控制参数。泵控子系统单神经元PID控制器框图如图2所示,具体的控制算法及学习算法如下:
(1)

图2 单神经元PID控制器框图
式中:u为神经元的控制输出;K为神经元的比例系数,且K>0;ηP、ηI和ηD分别为比例、积分和微分的学习速率;wi(i=1,2,3)为神经元的权值;xi(i=1,2,3)为神经元的输入;e为转速误差;z为神经元的教师信号;k为采样次数。
2.2 阀控子系统的RBF神经网络滑模控制
首先建立阀控子系统的三阶数学模型,然后基于奇异扰动理论对三阶数学模型进行降阶,最后基于降阶后的数学模型设计RBF神经网络滑模控制器,并证明系统的稳定性。
2.2.1 阀控子系统的数学模型
惯性负载的动态为
(2)
式中:m为负载质量;xl为活塞杆的位移;P1和P2分别为液压缸两腔的压力;Ap为有效作用面积;b为粘性阻尼系数;fd为难以准确建模的项,包括外部随机干扰力、未建模摩擦力、机械参数摄动等。
液压缸两腔的压力动态为
(3)
式中,V1为液压缸1腔的容积,V2为液压缸2腔的容积,βe为液压油的体积弹性模量,Q1和Q2分别而液压两腔的流量,Ci为液压缸的内泄漏系数。
在泵阀并联系统中,由于液压缸的流量由泵控子系统和阀控子系统共同提供,所以液压缸两腔的流量还可以表示为
(4)
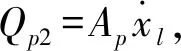
(5)
式中,fh1和fh2为广义扰动,包括泵控子系统的供油误差、伺服阀流量建模误差、未建模泄漏、液压参数摄动等。
伺服阀的流量方程为
(6)

由于伺服阀的频响相对于整个系统来说较高,故不考虑伺服阀的动态,则
xv=kvu
(7)
式中,kv为阀芯指令增益,u为控制输入。
(8)
式中,γ=kqkv。
根据式(2)-(8)可得阀控子系统的数学模型为
(9)
为了简化后续控制器的设计过程,使其更适用于工程实际应用,以下将基于奇异扰动理论[13- 15]对阀控子系统的数学模型(9)进行合理的降阶。
首先定义负载压力PL=P1-P2,根据式(5)可得
(10)
式中,ε=1/βe。

(11)
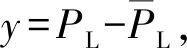

(12)

于是,降阶后的系统(9)变为
(13)
(14)

针对阀控子系统(14),如果采用传统滑模控制,必须知道α(·)与β(·)的准确值,然而由于液压系统的参数不确定性,许多参数例如粘性阻尼系数b、外部干扰力fd、广义扰动fh1和fh2以及内泄漏系数Ci等无法准确得知,导致需要基于准确数学模型的控制器设计出现困难。文中采用RBF神经网络分别估计未知函数α(·)和β(·),再结合滑模控制来完成阀控子系统控制器的设计。
2.2.2 RBF神经网络滑模控制器的设计
首先定义位置跟踪误差为e=x1-x1d,设计滑模面为

(15)
式中,c>0。
对s求导,可得
(16)
RBF神经网络估计未知函数α和β的具体算法为
(17)
式中,α和β为理想RBF神经网络输出,W*和V*分别为估计未知函数α和β的神经网络理想权值向量,hα(x)和hβ(x)分别为估计未知函数α和β的神经网络隐含层输出向量,hj为隐含层第j个神经元的输出,εα和εβ为网络的逼近误差且|εα|≤εαN、|εβ|≤εβN,x为网络的输入向量,cj为隐含层第j个神经元高斯基函数中心点的坐标,bj为隐含层第j个神经元高斯基函数的宽度,j=1,2,…,5。
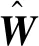
(18)
滑模控制律设计为
(19)
阀控子系统的RBF神经网络滑模控制器框图如图3所示。

图3 RBF神经网络滑模控制器框图
将控制律式(19)代入式(16)中,可得
(20)
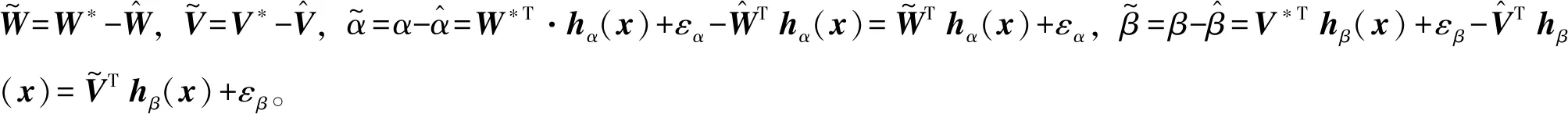
定义Lyapunov函数为
(21)
其中γ1>0、γ2>0,对式(21)求导,并结合式(20)可得
(22)
(23)
将式(23)代入式(22)中,可得
-ks2-η|s|+s(εα+εβu)
(24)

3 仿真研究
利用Matlab/Simulink和AMESim仿真平台搭建泵阀并联电液位置伺服系统的联合仿真模型,其中液压系统模型在AMESim中搭建,控制器在Matlab/Simulink中建立。AMESim中的液压系统模型综合考虑了液压系统泄漏、静摩擦、库伦摩擦、粘性摩擦、伺服电机惯量、电机与泵的连接刚度等因素。联合仿真模型见图4,仿真参数见表1。
阀控子系统RBF神经网络滑模控制器的参数取值如下:bj=0.1,γ1=100,γ2=100,c=[-0.06,-0.03,0,0.03,0.06;-0.2,-0.1,0,0.1,0.2],k=100,c=5,η=10-3;泵控子系统单神经元PID控制器的参数取值如下:ηP=50,ηI=10,ηD=15,K=3。为了验证所设计控制器的优越性,将阀控RBF神经网络滑模控制器、阀控滑模控制器和PID控制器三者作对比,其中阀控滑模控制器的参数为c1=50、k1=60、η1=10-4,阀控PID控制器的参数为P=60、I=50、D=1;将泵控单神经元PID控制器和泵控PID控制器两者作对比,其中泵控PID控制器的参数为P=100、I=10、D=0。
(1)算例1:跟踪0.1 Hz- 50 mm的正弦位置信号
首先对比泵控单神经元PID控制器和泵控PID控制器跟踪指令转速的性能。为了体现对比的公平性,该组仿真中的阀控子系统均采用PID控制。
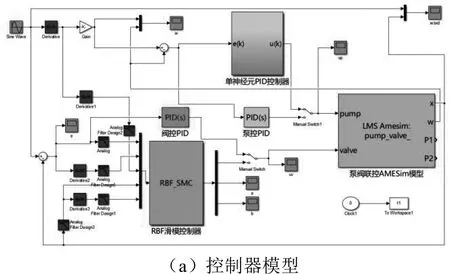
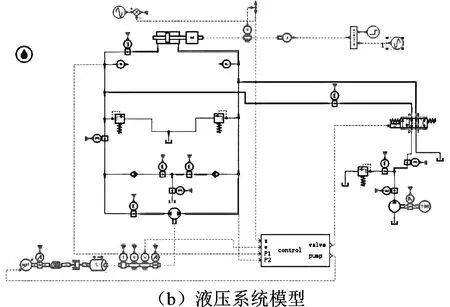
图4 Matlab/Simulink和AMESim联合仿真模型截屏

表1 泵阀并联电液位置伺服系统的仿真参数
由图5(a)和5(b)可知,在跟踪指令转速时,传统PID控制方法的误差为12 r/min,单神经元PID控制方法的误差为2 r/min,相比于传统PID控制误差减小了83.3%;由图5(c)可知,单神经元PID控制中的比例权系数、积分权系数和微分权系数都很快收敛到稳定值,3个权系数的稳定值分别为2.0、0.4和0.6。仿真结果表明,单神经元PID控制方法可以很好地进行PID权值系数的自适应,且具有较好的转速跟踪效果。
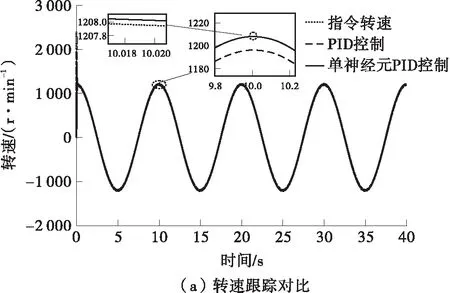


图5 两种泵控子系统控制方法的转速跟踪性能对比
接下来验证阀控子系统RBF滑模控制器的有效性。同样,为了体现对比的公平性,泵控子系统均采用单神经元PID控制器,阀控子系统则分别采用RBF神经网络滑模控制器、滑模控制器和PID控制器进行对比分析。
为了定量描述控制器的性能,文中定义了3个性能指标,分别为跟踪误差绝对值的最大值IAPE、跟踪误差平方的平均数IMSE、控制输出平方的平均数IMSC,其中IMSC代表控制输出的强度。3个指标的数学表达式如下:
(25)
(26)
(27)
在跟踪0.1 Hz-50 mm的正弦位置信号时,由图6(a)结果及表2中的IAPE指标可以得出阀控PID控制器的最大稳态跟踪误差为0.434 mm,阀控滑模控制器的最大稳态跟踪误差为0.254 mm,阀控RBF滑模控制器的最大稳态跟踪误差为0.109 mm。相比于PID控制器,所设计控制器的最大稳态跟踪误差减小了74.9%;相比于滑模控制器,所设计控制器的最大稳态误差减小了57.1%;且RBF滑模控制器的IMSE指标也明显小于PID控制器和滑模控制器。这说明所设计的控制器在整个工作周期的平均性能优于传统PID控制器和滑模控制器。由图6(b)结果以及表2中的IMSC指标也可以看出,RBF滑模控制器的控制输出小于PID控制器和滑模控制器的控制输出,说明所设计的控制器在需要较小控制量的前提下取得了更好的跟踪效果,这一指标进一步说明了所设计控制器相比于传统PID控制器和滑模控制器的优越性。图6(c)和6(d)分别为RBF神经网络逼近未知函数α(·)和β(·)的结果。
(2)算例2:正弦干扰力下,跟踪0.1 Hz- 50 mm 的正弦位置信号
为了测试阀控子系统RBF滑模控制器的抗干扰能力,在跟踪0.1 Hz- 50 mm正弦位置指令时加入0.1 Hz 500 N的正弦干扰力。为了比较的公平性,此组仿真中泵控子系统仍然采用单神经元PID控制器,阀控子系统则分别采用前述的3种控制方法进行对比分析。


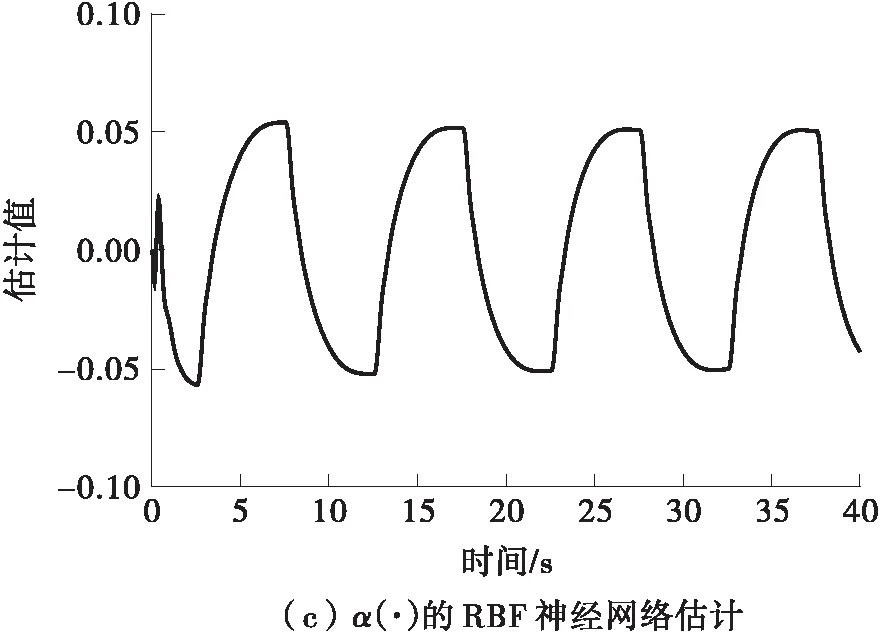

图6 3种阀控子系统控制方法的位置跟踪性能对比

表2 算例1的综合性能指标比较
由图7(a)结果及表3中的IAPE指标可以看出:在正弦干扰力下阀控PID控制器的最大稳态跟踪误差为2.00 mm,阀控滑模控制器的最大稳态跟踪误差为1.30 mm,阀控RBF滑模控制器的最大稳态跟踪误差为0.325 mm。相比于PID控制器,所设计控制器的最大稳态跟踪误差减小了83.8%;相比于滑模控制器,所设计控制器的最大稳态误差减小了75.0%;所设计控制器的IMSE指标也小于PID控制器和滑模控制器。这说明存在外部干扰力时,所设计控制器的平均性能仍然优于传统PID控制器和滑模控制器。由图7(b)结果以及表3中的IMSC指标可知,所设计控制器的控制输出小于PID控制器的控制输出,因为所设计的控制器具有一定的干扰估计与补偿作用,所以其控制输出会略大于滑模控制器,由此换来的控制性能的提升是值得的。综上可得,基于RBF神经网络的滑模控制器在存在干扰力时相比于其他两种控制器有更好的位置跟踪效果,且对干扰力具有更强的鲁棒性。


图7 存在干扰力时3种阀控子系统控制方法的位置跟踪性能对比

表3 算例2的综合性能指标比较
4 结语
文中以泵阀并联电液位置伺服系统为研究对象,考虑了参数不确定性和外部干扰力的影响,将智能控制方法应用于泵阀并联系统中,提高了该系统的位置跟踪性能。所做工作主要如下:
1)为泵控子系统设计了单神经元PID控制器,利用神经元的自学习功能可以为泵控子系统找到一组合适的控制参数;
2)为阀控子系统设计了基于RBF神经网络的滑模控制器,利用RBF神经网络去估计系统数学模型中的未知项,使得控制器的设计不再依赖系统的准确参数;
3)通过联合仿真验证了所设计的智能控制方法的有效性和优越性,即泵控子系统单神经元PID控制器相比于传统PID控制器具有更好的转速跟踪性能,基于RBF神经网络的滑模控制器相比于传统PID控制器和滑模控制器具有更高的位置跟踪精度与更强的鲁棒性。

