基于遗传算法的四轮转向-驱动汽车时变LQR控制

罗玉涛 周天阳 许晓通

(华南理工大学 机械与汽车工程学院，广东 广州 510640)

分布式驱动汽车可以通过四轮转向、转矩分配实现对质心侧偏角、横摆角速度等稳定性参数的有效控制，大大提高汽车在高速、低附路面等工况下的安全性，因此，基于四轮转向/驱动的主动安全控制技术自20世纪80年代以来成为了研究热点[1- 4]。Nagai[1]发现，四轮转向不仅可以提升汽车的低速机动性和高速稳定性，还能主动调整内外侧车轮的负荷分配，有利于极限工况下的主动安全控制；李彬等[4]基于最优控制理论设计了前轮转向与附加后轮转角系统，对质心侧偏角和横摆角速度进行了较好的控制；Xie等[5]基于变权重LQR(线性二次调节)算法设计了电子稳定控制器和后轮主动转向集成控制系统，避免了极限工况下的失稳。但是，在大转向下，基于线性车辆模型设计的附加后轮转角由于轮胎处于高度非线性区域而不足以维持车辆的稳定性，有鉴于此，许多学者提出了四轮转向和驱动综合控制策略。例如，冯源等[6]基于状态反馈设计了基于前馈转角和直接横摆力矩控制的汽车操纵性改善控制策略；还有学者[7- 8]依据分层控制的思想，依照稳定性控制需求设计四轮转向驱动协调控制策略，将控制量解耦为单独的四轮驱动力以及转向角，发挥了分布式驱动汽车在主动安全控制上的潜能；Nam等[9]设计了前轮主动转向以及四轮纵向力分配协调控制策略，通过实验证实转向驱动的协调控制可提高侧向稳定性；Shuai等[10]基于四轮独立驱动、四轮独立转向车辆对四轮独立驱动、制动、转向的集成控制算法进行了研究，利用滑模控制理论搭建了滑模控制器，从而获得车辆所需的理想侧向力和纵向力。但上述稳定性控制算法均是基于线性二自由度车辆模型来设计，对大转向角工况的适应性较差，不能真实反映轮胎非线性区域的动力学特性。国内外一些学者对轮胎状态估计做了许多研究，并将成果应用于主动安全控制策略中。Nam等[11]基于侧向力传感器实时监测轮胎状态，并依此设计了一种主动转向系统；刘启佳等[12]考虑到线性化参考模型在极限工况下不能反映轮胎特性，将轮胎刚度依据实际特性分为低、高两个区域，得出了变轮胎刚度模型实际控制效果更好的结论；Nagai等[13]应用模型匹配控制理论研究了主动前轮转向与横摆力矩集成控制算法，提高了车辆的操作稳定性；文献[14- 15]设计了无味卡尔曼滤波来对轮胎侧向力、侧偏角、纵向车速进行在线估计，并将估计值同步至H-∞鲁棒最优控制器中以提高工况适应性。Furukawa等[16]基于传递函数建立了后轮转角和附加横摆力矩关于车速、前轮转角的控制率，通过考虑轮胎非线性特性提升了转角转矩集成控制的鲁棒性。

针对当前多数研究都是基于线性参考模型、鲜有四轮转向和驱动综合控制的现状，文中建立了一种考虑轮胎非线性特性的LTV(线性时变)控制模型，并基于遗传算法线性二次调节对质心侧偏角和横摆角速度进行综合优化，以提升车辆行驶的稳定性。

1 总体控制策略

研究对象为四轮独立转向-驱动的分布式驱动汽车。首先建立考虑轮胎非线性特性的线性时变模型，以理想二自由度稳定性参数为控制目标，考虑参数整定对LQR控制器效果的影响，利用遗传算法优化权重矩阵，从而得到附加横摆力矩和四轮转角。计算由轮胎力决定的附加横摆力矩，采用规则分配的方式将其转化为四轮驱动力矩，总体控制策略如图1所示。

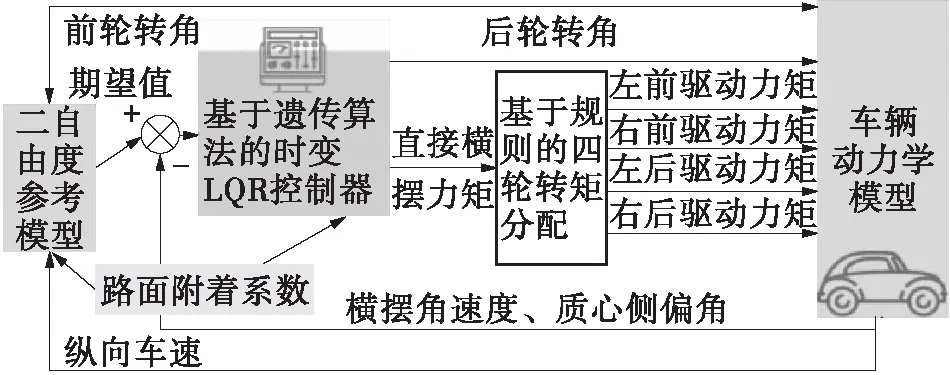
图1 高速车辆稳定性控制总体策略

2 线性时变控制模型的建立

2.1 二自由度车辆动力学模型

基于稳定性控制的转角转矩协调控制需要依赖二自由度动力学模型，考虑侧向、横摆的二自由度参考模型如图2所示。

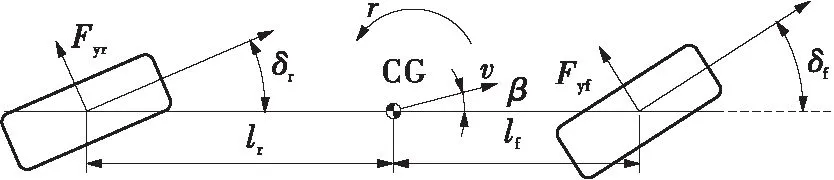
CG表示车辆质心，v为车辆行驶速度，r为横摆角速度，Fyf、Fyr分别为前、后轮胎侧向力

Fig.2 Two-degree-of-freedom vehicle reference model

依据文献[17]，同时将前后轴侧偏刚度视为时变值，可得动力学方程如下：

(1)

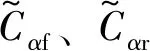
将式(1)改写为以后轮转角和附加横摆力矩为主动控制量的状态空间方程形式：

(2)

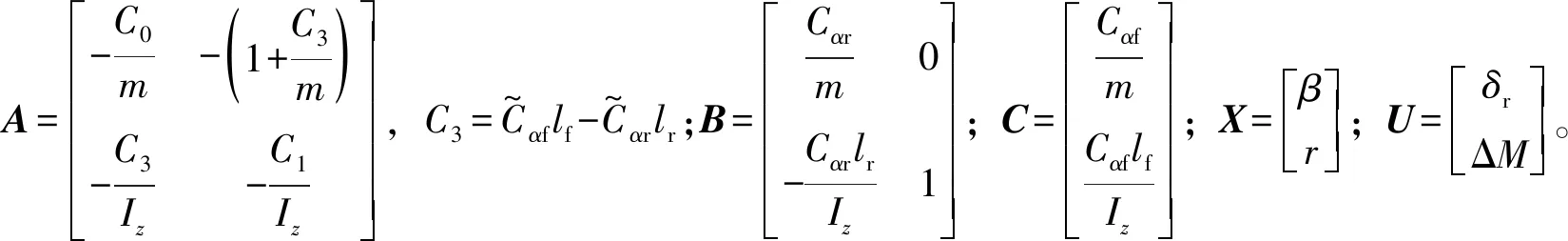
2.2 考虑轮胎非线性特性的时变控制模型的建立

有别于将轮胎刚度视为常数的线性定常二自由度参考模型，文中直接利用Carsim目标控制车辆中的轮胎模型，将轮胎分为线性区和非线性区以提高工况适应性。目标车辆前后轮的侧偏特性如图3所示。为了更好地体现轮胎刚度的时变特性，同时避免过多区域分段时变特性导致控制量输出的频繁跃动，进而对驾驶员造成过多的干扰，将轮胎侧偏特性分为线性区(轮胎侧偏角|α|≤0.04 rad)和非线性区(|α|>0.04 rad)，并将区域分界线记作αm=0.04 rad。

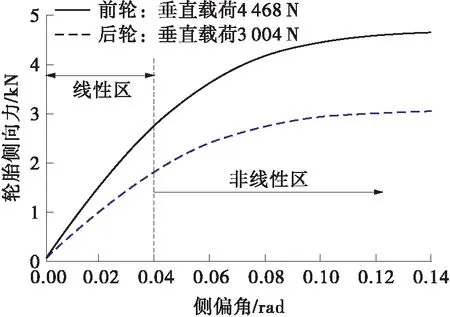
图3 目标车辆的轮胎特性及特性分区

选取区域内一组基于轮胎模型的数据点(αi,Fyi)，i=1，2，3，…，N，求解最小二乘问题，得到分区后的轮胎侧偏刚度Cαi(i代表fl、fr、rl、rr，分别表示左前轮、右前轮、左后轮、右后轮)，并将轴侧偏刚度定义为Cαf=2Cαfl、Cαr=2Cαrl。假定轴侧偏刚度与路面附着系数成正比，轮胎分段线性化的识别结果如表1所示。

表1 轮胎分段线性化识别结果

2.3 线性时变模型的建立

由式(2)可知，系统状态空间方程的控制结构矩阵A、B、C均依赖于前后轴实时刚度的解析，基于轮胎特性分区对A、B、C进行解析，可以建立统一的线性时变模型。

在轮胎线性(i=1)和非线性内(i=2)区域内，系统微分方程独立表示为

(3)

Ai、Bi、Ci的具体形式如式(2)解析。

为了将式(3)所表述的二自由度车辆动力学模型联立，引入跟随轮胎侧偏角变化的权函数，定义如下：

[w1w2]T=

(4)

式中：αlow=0.03 rad、αup=0.05 rad，分别为上、下切换阈值；α(t)为观测到的前后轴侧偏角较小值，

(5)

联立两个区域的动力学方程可以得到线性时变系统，由式(3)、(4)可得LTV系统的微分方程为

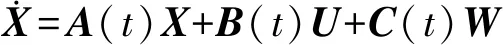
(6)

式中，A(t)=w1A1+w2A2，B(t)=w1B1+w2B2，C(t)=w1C1+w2C2。

3 基于遗传算法的时变LQR控制

3.1 控制目标

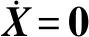
(7)

式中，rsteady为路面附着极限内的理想横摆角速度。

考虑路面附着极限以及侧向加速度的容许值，设定横摆角速度上限

rbound=0.85μg/u

(8)

综合式(7)、(8)，得到整个控制域内的理想横摆角速度rd如下：

(9)

将质心侧偏角与横摆角速度理想值记作向量Xd=[βdrd]T。

3.2 时变LQR控制策略的设计

文中采用线性二次型最优输出跟踪控制器设计后轮转角和附加横摆力矩的控制输入，定义状态量的误差向量如下：

(10)

式中，Xf为状态反馈向量，Xf=[βfrf]T，由Carsim观测得到。参考文献[12]，同时考虑控制过程累积误差和控制能量消耗，定义二次型指标

(11)

式中，Q和R为LQR协调控制器的加权矩阵，其中Q为半正定矩阵，R为正定矩阵。

利用变分法求解该二次型的最优解，最优控制规律为

U*(t)=-R-1BTPX-R-1BT(PBR-1BT-AT)-1(QXd-PCδf)

(12)

式中，P为线性系统相应黎卡提方程的解。

考虑线性时变模型的叠加性，时变最优控制量为

(13)

3.3 基于遗传算法的LQR控制性能优化

由式(13)可知，LQR对质心侧偏角和横摆角速度的协调控制效果依赖于状态量权重参数的选择，要求在低附路面下保证车辆质心侧偏角控制效果更好，以防止车辆侧滑，高附路面下则侧重于对理想横摆角速度的跟随，以保证较好的转向特性。为此，设计基于遗传算法的LQR控制优化算法，定义适应度函数以实现累计跟踪误差最小的控制目标：

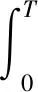
(14)

基于遗传算法的优化变量为状态量权重矩阵Q，记作

(15)

设置如表2所示的遗传优化参数，其中qv、qr的初始值在上下限产生，由于遗传算法的在线计算耗时无法满足实时控制或仿真实验的需求，因此通过离线仿真获取特定工况下的遗传算法最优解，结合模糊逻辑或在线插值等方法来提高方法的工况适应性，以满足实时控制的需求。以路面附着系数分别为0.8、0.5的工况为例进行仿真，计算适应度函数，并通过迭代来求解最优权重矩阵。

以附着系数为0.8的路面为例，遗传算法迭代优化过程中，适应度函数的变化如图4(a)所示，遗传算法优化下的qv、qr最优解如图4(b)所示。

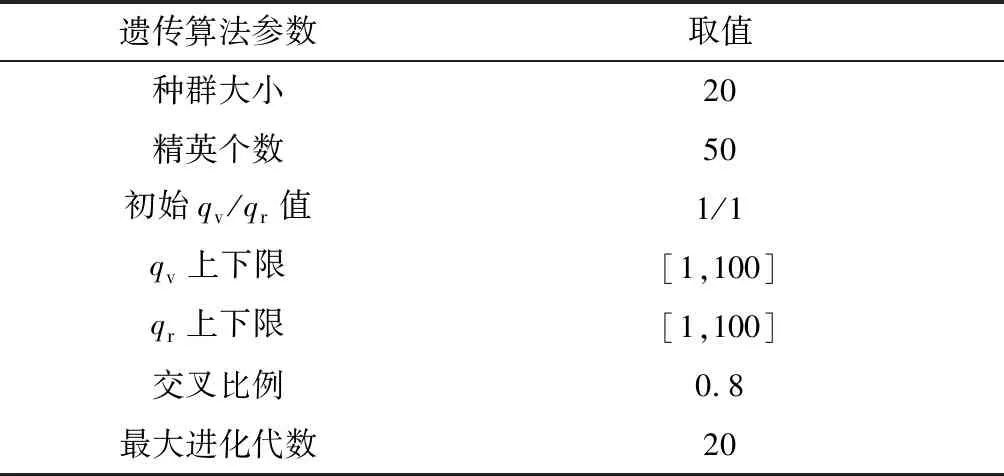
表2 遗传算法优化参数的设置

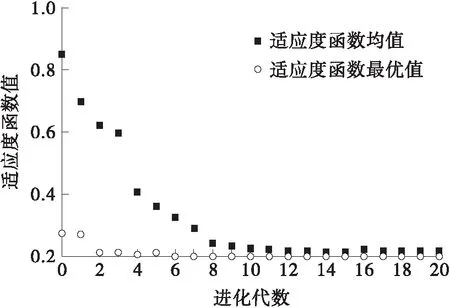
(a)适应度函数随进化代数的变化

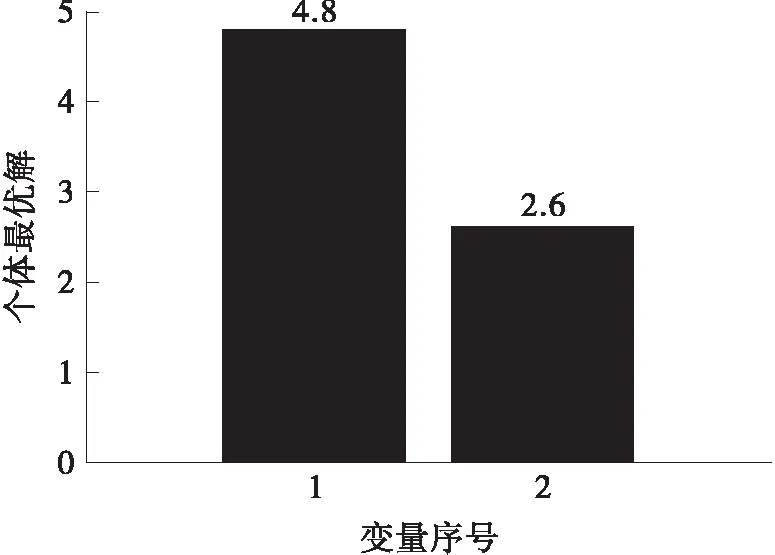
(b)权重系数最优解

两种路面附着系数下的权重矩阵优化结果如表3所示。

表3 基于遗传算法的权重矩阵优化结果

3.4 底层四轮转角及转矩分配

四轮转角分配应满足理想阿克曼转角几何关系，如式(16)所示：

(16)

左右轮差动形成附加横摆力矩，通过规则分配使前后轴各产生一半的附加横摆力矩，并将纵向力转化为独立驱动转矩，四轮转矩存在式(17)所示关系及约束：

(17)

s.t .|Ti|≤Tmax。

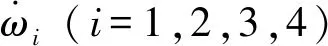
4 仿真分析

Carsim采用了AB Dynamics、TNO Automotive等公司针对汽车各零部件的测量数据，依据相关数据及理论建立了涵盖轿车、SUV、跑车、拖车等多种车型的非线性多自由度车辆模型，因此具有实车级的仿真精度，被广泛应用于底盘主动安全控制方法的研究中，可以实现对一些因计算量大、求解困难以及实车开发难度大而难以在实车中应用的控制方法进行快速验证。文献[18]利用Carsim对所提出的转矩矢量分配控制策略进行了验证，张博等[19]在Simulink-Carsim联合仿真环境下对电动主动转向系统的效果进行了分析，Li等[20]利用Carsim高保真整车模型对所提出的基于深度学习和数据融合技术的脑启发运动控制系统进行分析，证明了控制系统对延迟和噪声造成的影响有较好的抑制作用。实际应用效果表明，Carsim仿真平台是科研院校面对算法在实车中应用困难或者实车开发难度大的情况可采取的一种重要研究手段。为了验证所提出的基于LTV模型的控制系统以及LQR控制器的有效性，文中在Simulink/Carsim仿真环境中搭建基于遗传算法的时变LQR控制器(LTV-LQR)及整车动力学闭环仿真模型。

4.1 时变LQR控制器性能分析

为了验证LTV-LQR控制器的效果(计算机硬件环境下，不关注方法的实时性效果)，将其与线性化二自由度模型(Lin-LQR)以及无控制情形(前轮转向2WS)进行对比仿真，仿真工况设置为：车辆在路面附着系数为0.8的道路以72 km/h的车速行驶，在0 s对前轮施加0.08 rad的转角。为了观察LTV模型的切换点，将转角上升时间设置为1 s。LQR权重参数采用遗传算法进行优化后输出。仿真结果如图5所示。

由图5(c)可知，在仿真开始的0.5 s左右，权函数值开始切换，轮胎由线性区域过渡到非线性区域，二自由度线性模型由于假设轮胎侧偏刚度线性化，因此后轮需要较大的转角输出才能抑制质心侧偏角的增大，而LTV模型充分考虑了轮胎的非线性特性，在非线性区转角的控制效果明显弱化，因此后轮转角小于Lin-LQR控制器的输出值，如图5(b)所示。为了对非线性区域后轮转角控制效果的减弱进行补偿，LTV-LQR控制器输出更大的附加横摆力矩以提高对质心侧偏角的控制。由图5(e) 可知，在高车速下阶跃转角的输入会使侧向加速度负向迅速增大，不利于驾驶员的转向视野，而Lin-LQR控制和LTV-LQR协调控制都可以使质心侧偏角回正，但LTV-LQR控制的效果要优于Lin-LQR。由图5(f)可知，无控制下的前轮转向横摆角速度过大，车辆会发生激转，而LTV-LQR控制方案对理想横摆角速度具有最好的跟随效果。前轮转角阶跃输入下的控制效果对比如表4所示。由表4可见，相较于Lin-LQR，LTV-LQR协调控制策略将质心侧偏角稳态值由0.020°进一步控制到0.006°，对稳态理想横摆角速度的跟随效果提升了3.01%，同时有效避免了无控制下的车辆激转。

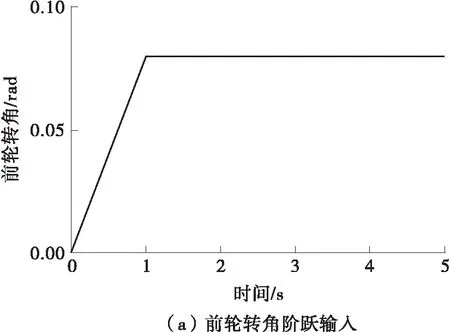
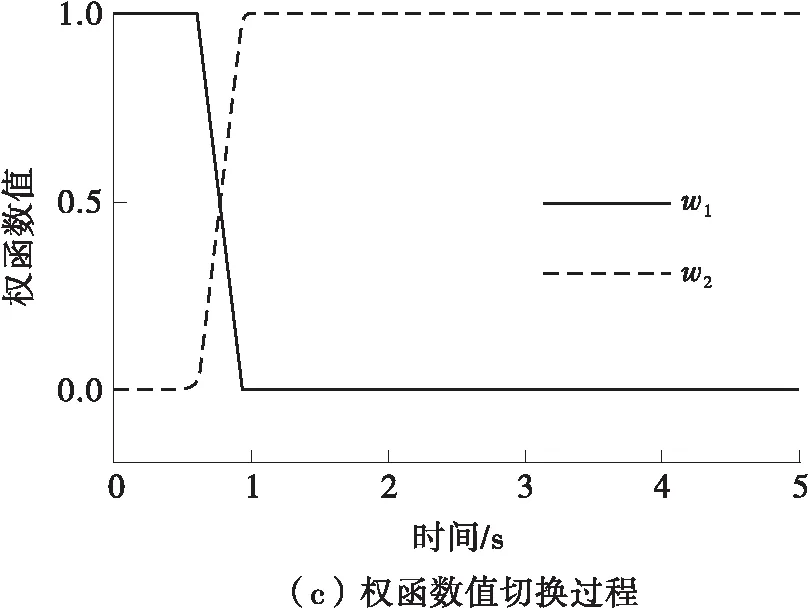
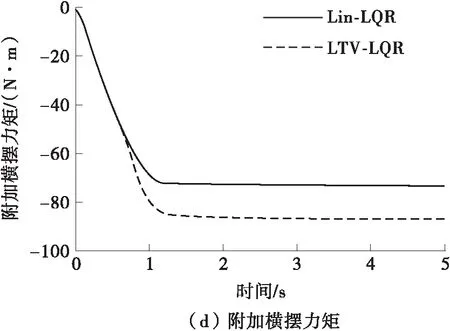
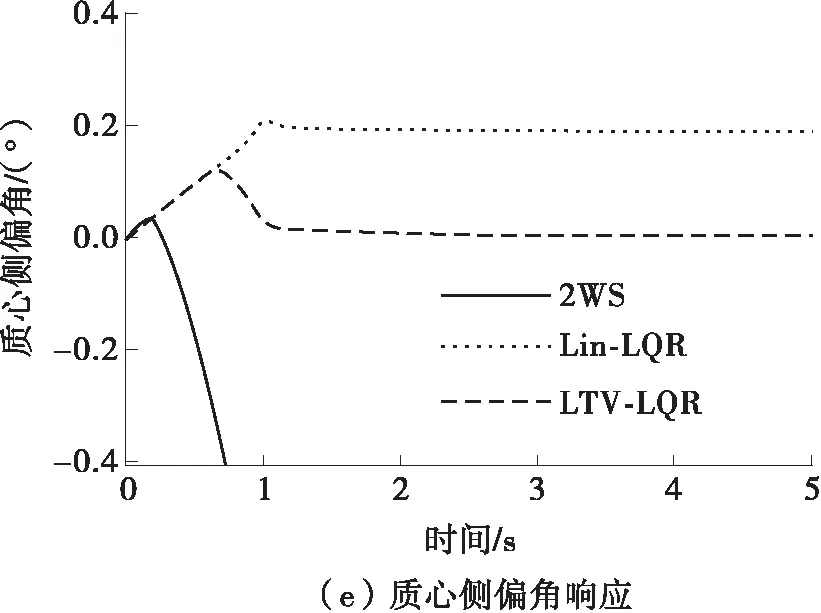
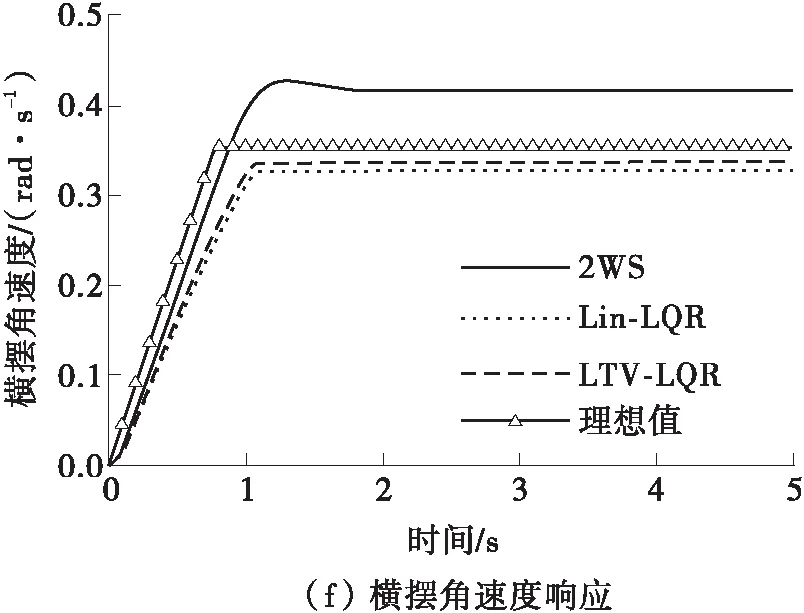
图5 前轮转角输入下的LQR控制仿真结果

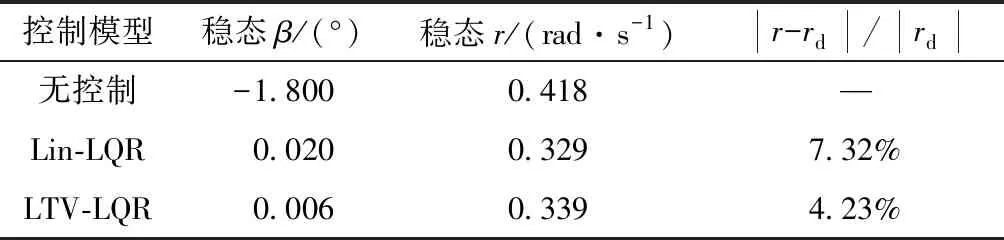
表4 前轮转角阶跃输入下的控制效果对比

4.2 人-车闭环双移线变道下的LTV-LQR控制仿真

为了验证所提出的LTV-LQR控制器在系统级整车平台上的控制效果，借助Carsim双移线仿真工况对该协调控制策略进行验证。仿真工况设置为：在路面附着系数为0.5的路面以80 km/h进行双移线变道，即模拟低附路面进行两次快速变道。该工况不仅要求车辆有较好的动力学特性以防止在高速行驶同时转向的情况下发生失稳，还要求车辆有较好的轨迹保持能力，在换道过程中能正确地处于道路边界线内。LTV-LQR控制器的参数由遗传算法离线迭代获得。

在换道工况下四轮转角转矩LTV-LQR协调控制输出的转角及附加横摆力矩见图6。由图6(a)可知，由于加入了与车辆系统闭环的驾驶员模型，因此在附加后轮转角和转矩的情况下，前轮转角会依据驾驶员模型实时调整；而且，由于前轮转角并不是相同的，可以发现，2WS车辆的前轮转角要大于施加转角转矩控制后驾驶员模型输出的前轮转角，使得前轮转向车辆在高速低附路面下转向发生侧滑失稳，驾驶员必须通过施加大方向盘转角来让车辆回稳，使车辆保持稳定状态。

由图6(b)、6(c)、6(f)可知，LTV-LQR控制器会输出与横摆角速度符号相反的附加横摆力矩以防止横摆角速度过大而激转。前轮转向汽车在5s左右(变道回正)由于轮胎处于强非线性而导致侧向力不足，出现质心侧偏角急剧加大的侧滑现象，而LTV-LQR协调控制器通过四轮转矩转角控制实现质心侧偏角的抑制。由图6(f)可知，横摆角速度在协调控制下对理想值的跟随比较好，综合控制效果体现在图6(g)所示的双移线变道轨迹中，可见，未施加转角转矩协调控制的车辆轨迹偏差较大，而施加LTV-LQR控制的车辆的轨迹跟踪效果更好。借助Carsim将结果可视化，截取4帧变道同一纵向位移下的车辆姿态，得图7所示轨迹。可见，LTV-LQR控制下，车辆变道时的车身姿态保持得更好。

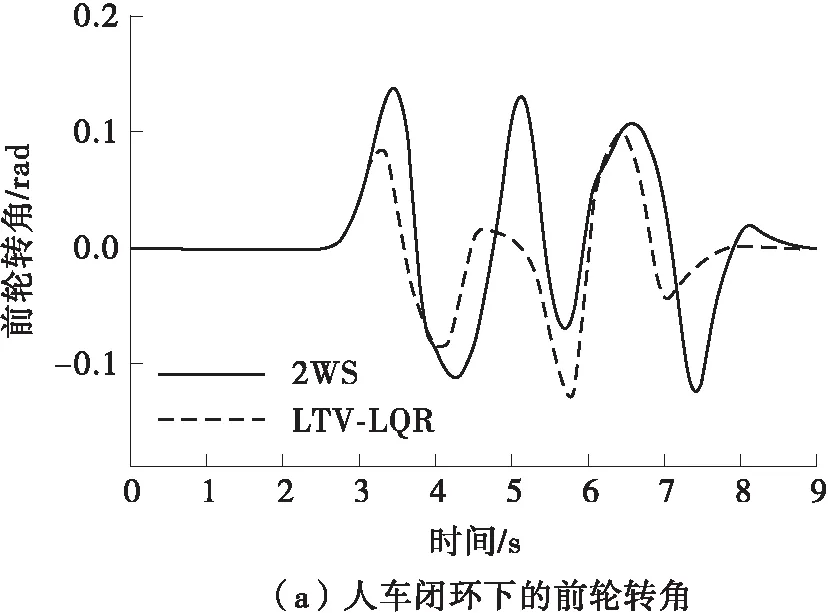
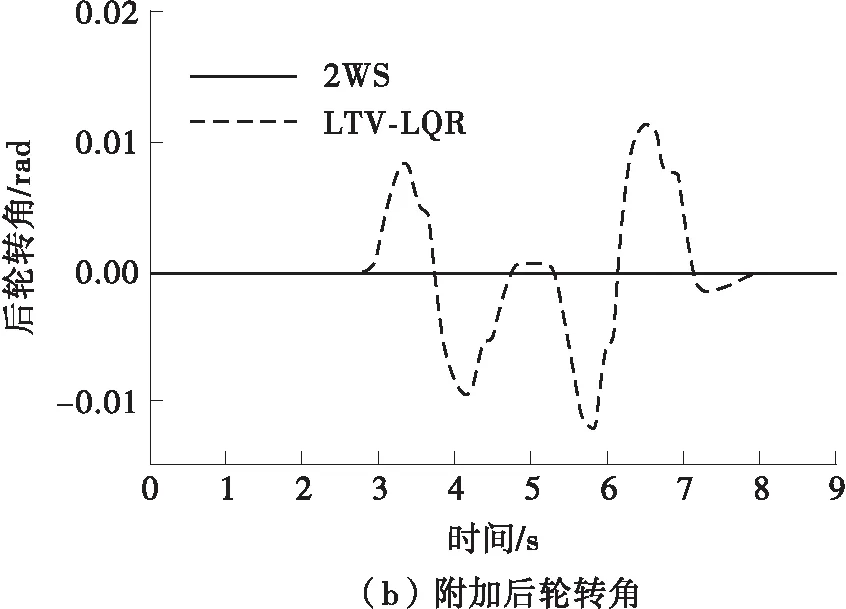
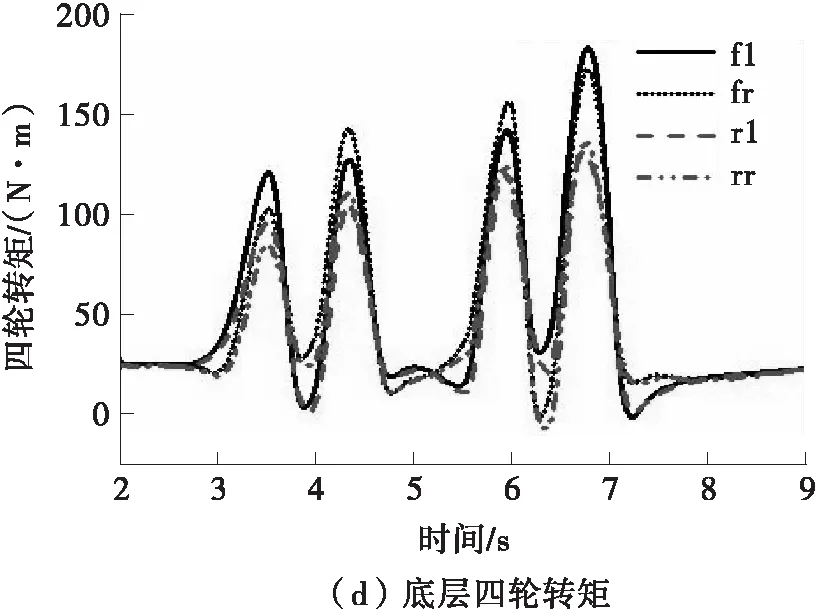
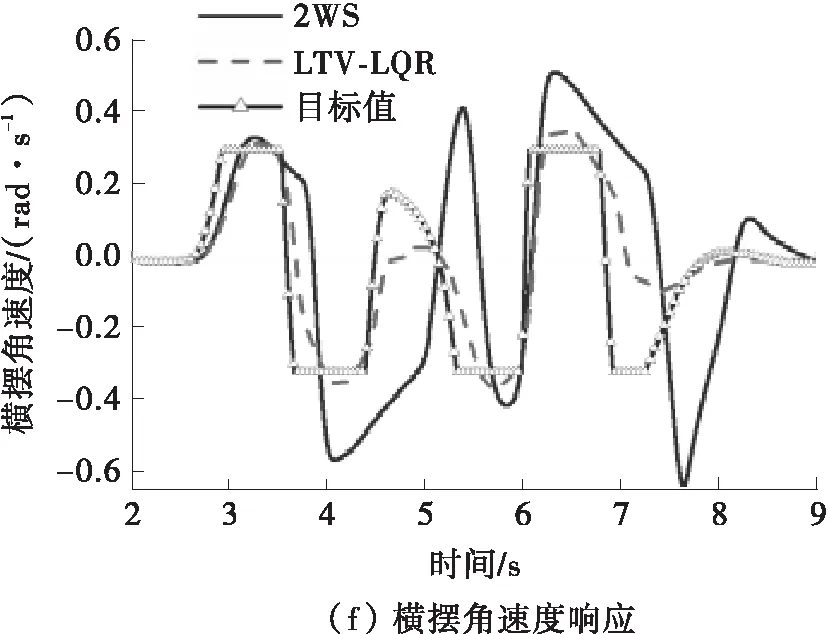
图6 双移线工况下的LQR控制仿真结果

将未施加转角转矩协调控制的车辆与施加LTV-LQR协调控制的车辆的控制效果进行对比，结果列于表5。可以看出，LTV-LQR控制策略既能有效地优化车辆稳定性参数，又能将最大侧向位移跟踪误差由0.65 m控制到0.36 m，轨迹跟踪效果提升了44%。

图7 Carsim可视化车辆双移线变道轨迹

表5 低附路面双移线工况下LQR的控制效果对比

5 结论

文中针对车辆高速转向等稳定性差的工况，提出一种基于遗传算法的时变LQR转角转矩协调控制策略，并在Simulink-Carsim环境下验证了该控制策略在工程级试验平台的有效性，得出以下结论：

(1)相较于线性化的LQR控制策略，基于线性时变模型设计的LQR控制策略对车辆质心侧偏角和横摆角速度的控制效果更好，能有效保证车辆在高速转向时有较好的稳定性；在给定的前轮转角阶跃输入下，基于线性时变模型的LQR控制策略能有效将车辆质心侧偏角稳态值由0.020°进一步控制到0.006°，对稳态理想横摆角速度的跟随效果提升了3.01%。

(2)在Simulink/Carsim系统级整车仿真环境中，所提出的LTV-LQR协调控制策略能有效地完成低附路面下的高速双移线变道工况，并对车辆质心侧偏角和横摆角速度进行有效的优化，避免了无控制前轮转向车辆易发生的侧滑、激转现象，同时提高了对理想双移线轨迹的跟踪精度，最大侧向位移误差由0.65 m控制到0.36 m，轨迹跟踪控制效果提升44%。