基于激光点云的高墩垂直度偏差分析方法

董永泉，袁亚通

(重庆交通大学 土木工程学院，重庆 400074)

伴随着中国交通运输事业的快速发展和科学技术实力的日益提升，越来越多世界级的桥梁相继问世，桥梁作为交通的咽喉要塞，重要程度可见一斑。桥墩作为整座大桥的脊梁，将上部结构全部荷载传递到基础上，其质量的好坏直接影响着桥梁的整体服役寿命。伴随着施工工艺的提高，桥墩的修建高度也是日益增高，被誉为“亚洲第一高敦”的赫章特大桥桥墩的高度达到惊人的195 m[1]。其中，桥墩垂直度偏差问题历来是中外学者的研究重点[2-5]，铁怀民等[6]利用有限元模型对桥墩垂直度偏差问题进行了量化分析，结果表明桥墩垂直度偏差对桥墩的抗裂性能和承载能力影响较大；丁克良等[7]采用全站仪自由设站无接触测量方法，实现了桥墩垂直度的快速测量；邱冬炜等[8]通过改进最小二乘拟合圆曲线的方法，快速检测分析桥墩垂直度。上述研究的主要依据是全站仪测量得到的少数数据值，但是桥墩作为一个三维立体结构，在修建过程中，最大偏差值出现的位置不可预测，依靠全站仪测量的有限个点来确定桥墩垂直度的方法存在缺陷，测量结果的实用性不强。实际上，桥墩的垂直度偏差检测问题并没有得到有效解决。

三维激光扫描技术作为继GPS技术之后的另一次技术革新，已经被广泛应用于变形监测领域[9-10]。三维激光扫描技术可以快速获取结构表面特征，并且具有数据精度高、后期处理简易等优点。黄承亮[11]将三维激光扫描技术和桥墩垂直度检测进行结合，利用三维激光扫描的优势对桥墩垂直度进行间接测量，并得出桥墩垂直度偏差。该研究的重点主要集中在三维激光扫描应用于桥墩垂直度测量的可行性上，对垂直度偏差的计算方法并没有做详细阐述，计算得到的桥墩垂直度数据少，因此无法保证桥墩垂直度检测结果的准确性。

现以三维激光扫描技术为基础，以空心薄壁矩形高墩为研究对象，利用扫描仪获取桥墩姿态，从桥墩全局信息出发，结合编程算法分析计算得到桥墩各个水平截面垂直度信息，总结其垂直度偏差存在的规律，对桥墩垂直度问题进行深入研究。

1 垂直度偏差分析基本思路

空心薄壁矩形桥墩具有非常强的几何性，故可把现实中的求桥墩垂直度问题转化为几何学中求取三维结构中心线问题。线由无数个点构成，在数学中，求解点的坐标往往要比直接求取三维曲线简单得多。故笔者利用降维法再把求取桥墩三维中心线问题转化为求取平面中心点问题，中心点便是桥墩水平截面特征点。将桥墩按水平向切割成若干个小矩形，再利用几何学原理求解矩形的形心，最后求得各个截面的形心到理论中心点之间的距离，即桥墩偏差值。

点云是由无数个带三维坐标的点构成的集合，在处理点云时，可大致分为准备数据、数据分析和结果分析3个阶段。数据处理流程如图1所示。

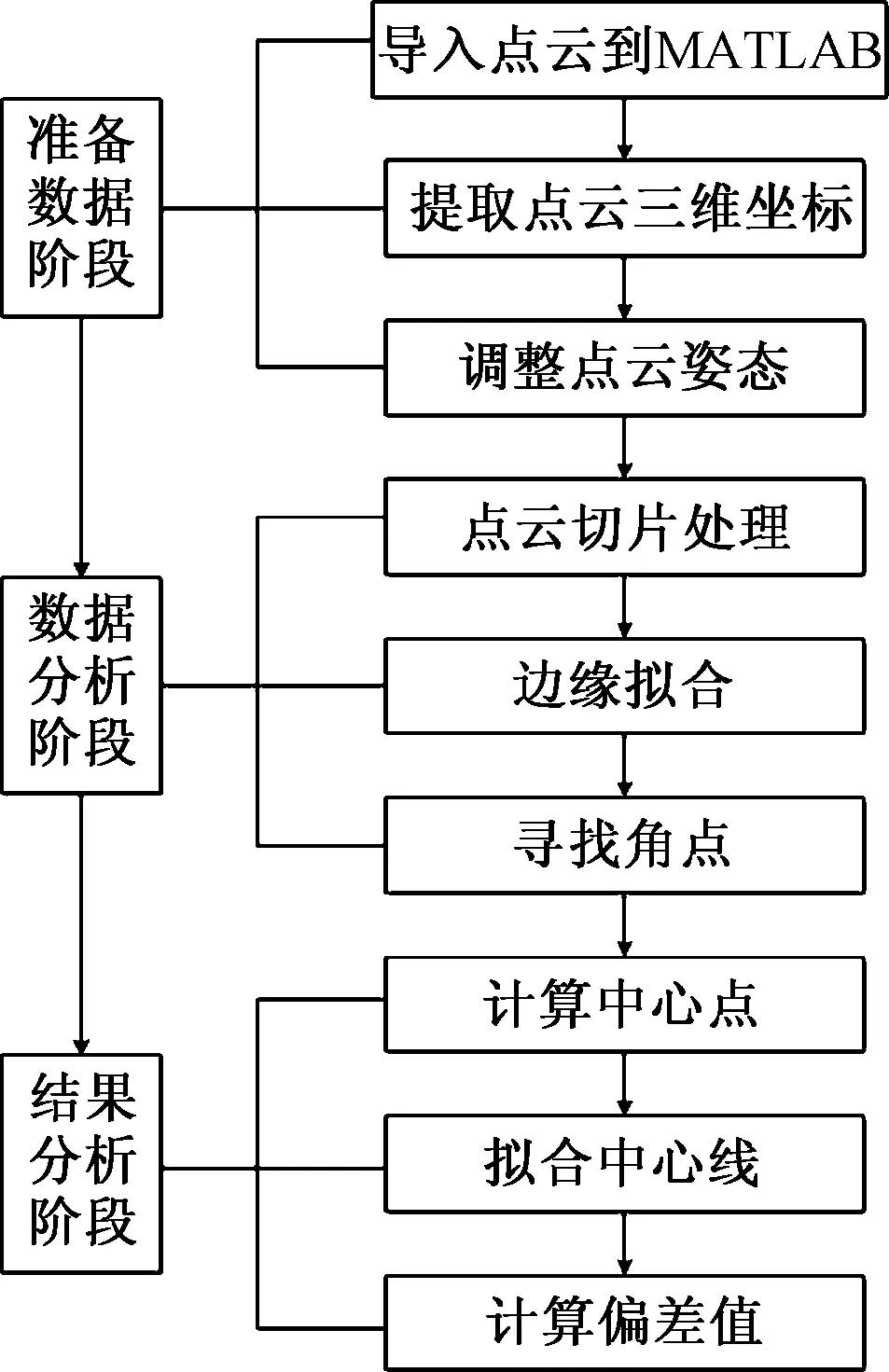
图1 数据处理流程

2 数据采集与预处理

2.1 点云数据采集方法

研究对象是某特大桥56号桥墩，该桥具有高达66.50 m的超高墩，位于中国高海拔地区，夏季昼夜温差大，施工周期长且施工期间风力较大。桥墩现场扫描情况，如图2所示，从图中可以看出，桥墩在分节浇筑过程中受外界环境影响可能会导致施工工艺不能满足技术要求，产生较大的水平偏差，传统的测量桥墩垂直度的方法不能全面反映桥墩偏差情况，三维激光扫描技术可以全面捕捉结构的表面特征，赋予结构物位置参数，很好的弥补全站仪单点测量的不足之处。

图2 现场扫描

为保证扫描精度要求，采用Faro X330扫描仪对桥墩进行扫描时，需对扫描仪点云间距和质量等参数进行合理的设置，同时设置6个站点和3组靶标球点位，并将设站精度控制在2 mm范围之内，如图3所示。测站点1～6围绕在高墩周围，且距离高墩约30 m，在6个站点之间分别放置3组靶标球，第1组靶标球与测站点1、2保持通视，第2组靶标球与测站点1、2、3保持通视，第3组靶标球与测站点3、4、5、6保持通视，保证每一站所采集的数据都至少有一组靶标球点云数据，同时要确保两站之中同名点云的数量，这样既方便点云拼接，减少作业时间，又能够满足拼接精度要求。

图3 扫描方案

2.2 点云数据预处理

经过外业采集得来的数据含有大量噪点，如桥墩底部围栏点云、塔吊点云、因外界环境变化产生的冗余点等。若不对噪点进行处理，分析桥墩垂直度时，额外的噪点会对算法产生一定的影响，最终影响垂直度的计算。常用的降噪算法有两种，分别为统计滤波算法和半径滤波算法。鲁东东等[12]对两种方法的点云降噪效果做了对比分析，对于桥墩结构，统计滤波算法能更好地完成降噪工作，但是由于算法自身的局限性，附属设施的点云不能被清除，在利用算法对点云进行机制层面的降噪后，需将点云导入Geomagic Control中，通过人机交互的形式删除噪点，保留56号桥墩点云，点云预处理前后对比如图4所示。

图4 点云预处理前后对比

3 点云数据处理

3.1 提取节段中心点

点云在坐标系中的初始位置不利于计算节段中心点，提取节段中心点之前需对桥墩进行姿态调整，使桥墩竖直方向与z坐标轴平行，首先将点云导入到MATLAB中，取出可以代表桥墩方向的向量，计算与向量(0，0，1)之间的夹角θ，随后利用旋转公式对点云进行调整，旋转公式为

(1)

(2)

(3)

式(1)、式(2)、式(3)分别为绕x、y、z坐标轴的旋转公式。式中x′、y′、z′为旋转后的坐标值；x、y、z为旋转前坐标值；θ为应旋转角度。调整姿态示意图如图5所示。

图5 桥墩姿态调整示意图

调整点云姿态的目的是将点云进行更为合理的分割。节段点云高度太大、分节太少，会使得数据信息不连贯，无法反映桥墩垂直度的真实状态。节段点云高度太小、分节太多，会占用大量计算资源，从而降低处理数据的效率。取0.2 m为一个节段高度较为合理。然后取出点云z坐标，按从低到高的顺序依次将点云分割为332个节段。桥墩某节段点云，如图6所示。然后对点云进行降维处理，三维点云平面化，得到可拟合状态下的点云。

图6 节段点云

由于桥墩带倒角，在进行四边直线拟合时，是否考虑倒角处的点云将会影响到直线拟合的精度，最终会对中心点的精确位置产生影响。目前最常用的直线拟合方法有两种，分别是RANSAC算法拟合和最小二乘法拟合。传统的最小二乘法拟合直线是以全部样本点作为计算对象，对全部样本点进行迭代分析，得出拟合直线。倒角处点云为非样本点，利用最小二乘法进行直线拟合时要对节段点云进行倒角切除操作，如图7(a)所示。最小二乘法拟合直线的过程不再赘述。

图7 点云分离示意图

RANSAC算法又叫随机抽样一致算法，假设给出的样本数据分为正常数据和异常数据，用迭代法从全部样本数据中估算出只包含正常数据的数学模型的参数，从而实现对样本数据的数学建模。

在利用RANSAC算法进行直线拟合时，要进行点云的切割，分离出一边以及两个倒角处的点云，如图7(b)所示。从图中可以看出，此组点云包含倒角处的异常点云数据。根据RANSAC算法原理，假设被分离点云数据为{(xi,yi),i=1,2，…,m}，随机选取两个点(x1，y1)、(x2，y2)，并求得过两点的直线方程Ax+By+C=0，设直线宽度为2ε，然后求出每个样本点与直线之间的误差Δd，公式为

(4)

记录Δd小于ε的点的个数S。按照点云数据量的大小合理的设置迭代次数d，直到找到S最大的一组数据并输出最佳参数Gk和Gb(Gk和Gb为最佳拟合直线的斜率和截距)。

最小二乘法拟合直线和RANSAC算法拟合直线效果对比，如图8所示。

图8 拟合效果对比

从图8中可以看出，最小二乘法对数据质量要求苛刻，必须舍弃桥墩倒角处点云。相比之下RANSAC算法鲁棒性更强，对数据质量更包容，更适合求桥墩中心点。故笔者采用RANSAC算法拟合的直线数据作为求中心点的依据。

在利用更先进合理的RANSAC算法进行完直线拟合之后，联立邻边两条拟合直线的方程，分别求得4个角点的位置坐标，最后利用4个角点的位置关系得到中心点坐标，如图9所示。

图9 桥墩节段点云中心点

3.2 垂直度偏差分析

节段中心点代表桥墩此节段实际中心位置，桥墩点云刨面图如图10所示。从图中可以清晰地看出桥墩的偏离情况，当桥墩修建高度达到40 m时，开始出现较大的偏移，随后在施工过程中进行了一定的修正。

图10 桥墩点云剖面图

由于缺少理论中心线作为参考，故不能具体求得桥墩各个截面的偏差值。笔者以桥墩底部为参照依据，取底部20个点的均值为理论中心点，以此为基础进行偏差分析。

底部20个中心点坐标如表1所示，分别求得x方向和y方向上的均值。

表1 桥墩中心点坐标

(5)

点(39.15，33.12)即为桥墩理论中线点，桥墩中心线方程为

(6)

已知直线方程便可求得已知点到直线之间的距离，因为此直线平行于z坐标轴，为简化计算过程，将直线长度设为1 m，利用海伦公式求得中心点到理论中心线的距离。

(7)

式中：a、b、c为三角形的3个边长；S三角形的面积；h为三角形的高。

中心点到理论中心线之间的距离即为偏差值，为便于分析垂直度变化规律，将理论中心线置零，使得桥墩高度与垂直度一一对应。

偏差延高度分布如图11所示。从图中可以看出，当修建的桥墩高度小于10 m时，桥墩偏差小于10 mm，随后偏差值随桥墩修建高度的增加不断扩大，桥墩修建高度达到30 m后，垂直度偏差值出现不稳定状态，波动明显，修建高度到达45 m处时，出现最大偏差。当桥墩修建完毕时，桥墩顶部偏差值不足20 mm，与最大偏差值相去甚远。

图11 偏差值延高度分布

桥墩偏差如图12所示。从图中可以看出，桥墩横桥向和顺桥向的偏差都小于30 mm。桥墩的倾斜并不是延横桥方向或延顺桥方向，而是在顺桥向和横桥向都有偏差，并且偏差的走向较统一。

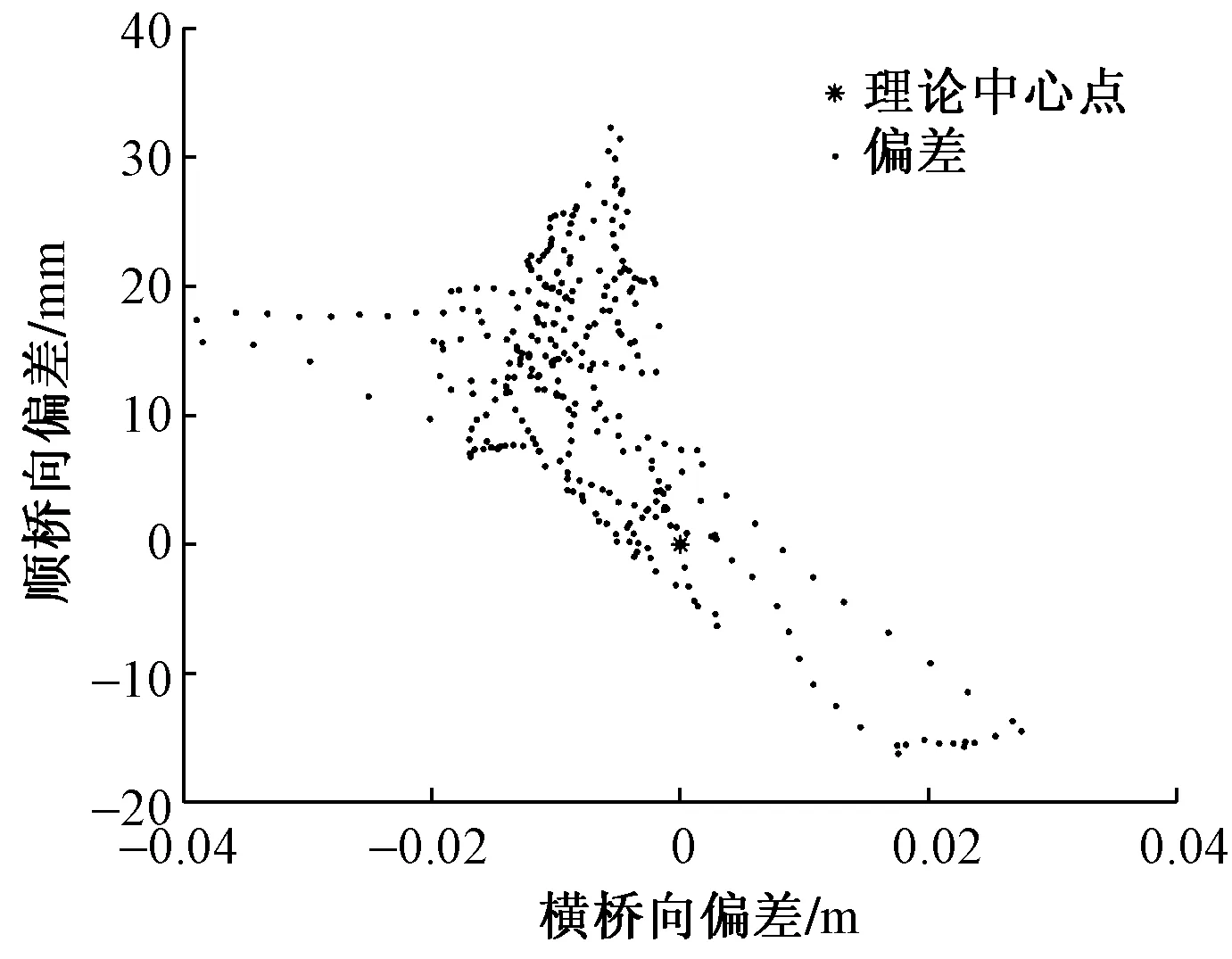
图12 桥墩偏差

横桥向偏差如图13所示。桥墩高度在50 m之内，横桥向桥墩偏差较小，偏差波动小；当桥墩修建高度超过45 m之后，偏差波动幅度变大。

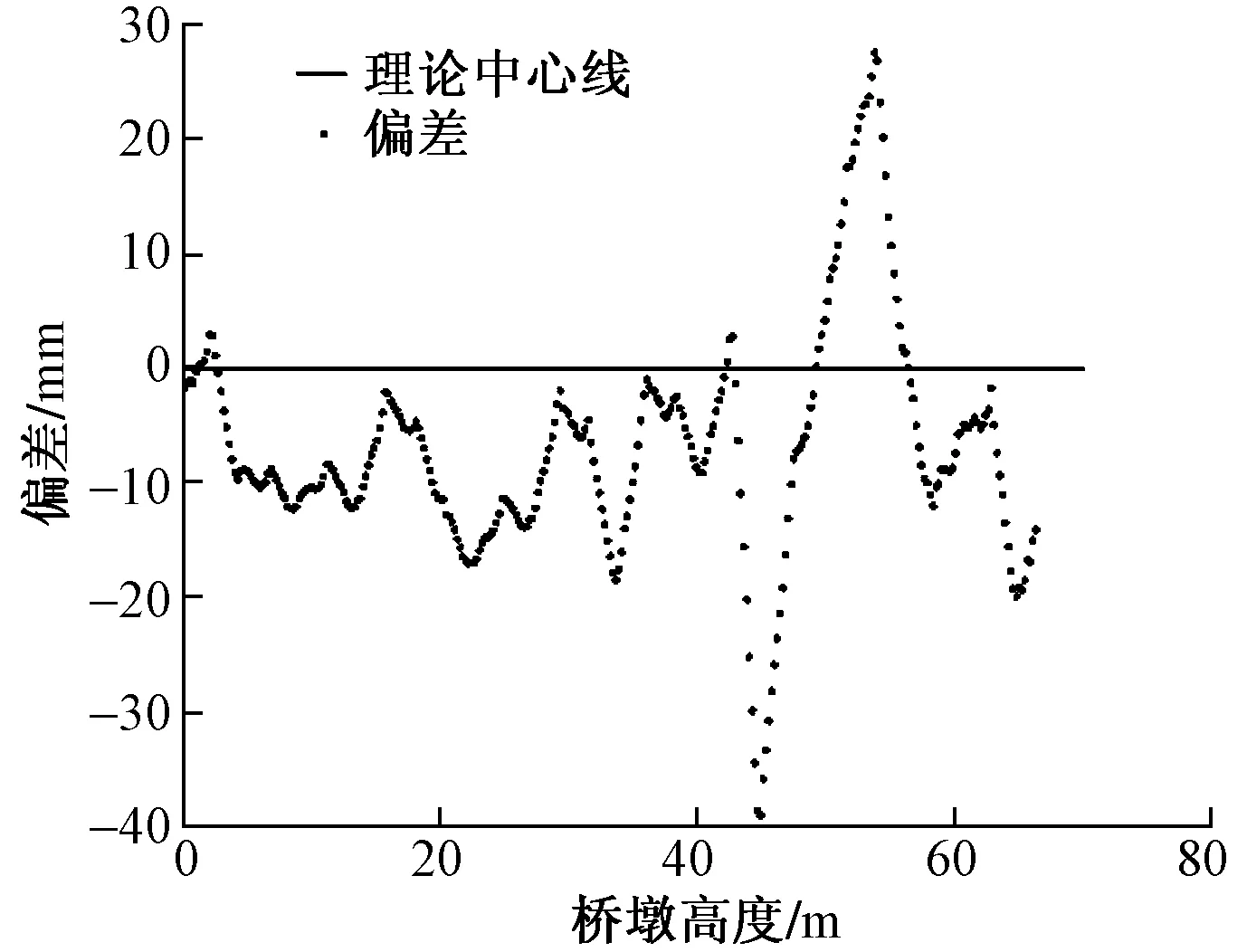
图13 横桥向偏差

顺桥向桥墩偏差如图14所示。在修建桥墩的全过程，偏差都不稳定，偏差波动幅度大。

图14 顺桥向偏差

3.3 对比分析

根据《公路桥涵施工技术规范》，桥墩质量检验标准中规定桥墩的垂直度允许偏差应满足0.3%H且不大于20 mm(H为建筑物全高)。墩顶高度处偏差为18.3 mm，显然合乎规范要求，但是全桥墩最大偏差却出现在45 m高度处，偏差为42.6 mm，已经明显超出规范要求。

利用全站仪测量获得10、20、30、40、50、60 m处的高度偏差，并与算法计算分析出的相应高度范围内最大偏差数值做对比，如表2所示。根据表2数据绘制偏差柱状图和误差折线图，如图15所示。

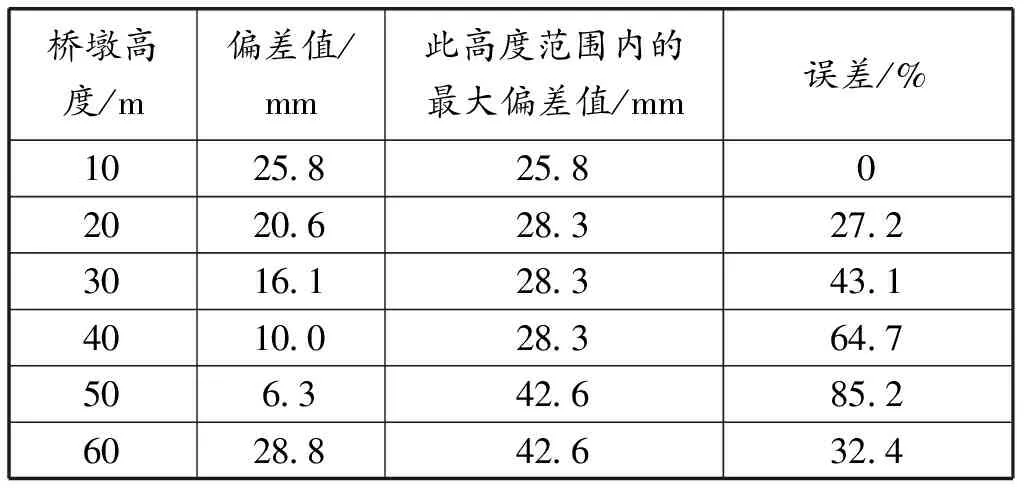
表2 偏差对比

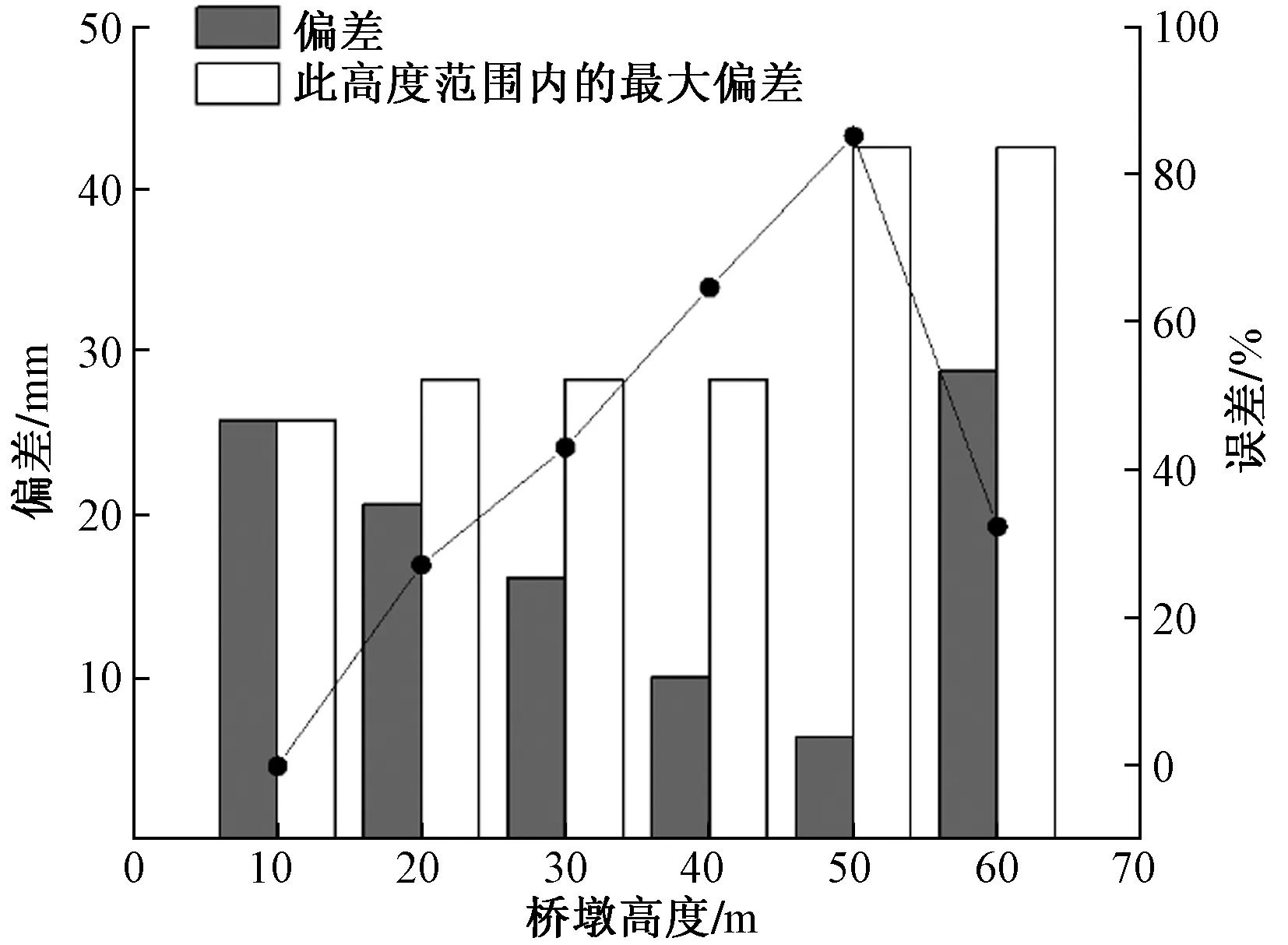
图15 偏差对比

表2和图15中的误差是偏差和最大偏差之差与最大偏差的比值。误差反应桥墩垂直度测量结果的可信程度，误差越大可信程度越小，误差越小，测量结果和真实值越接近，测量结果越可信。当桥墩高度为10 m时，偏差即为最大偏差，误差为0。此时测量的桥墩垂直度准确。当桥墩高度达到20 m时，偏差和最大偏差出现差距，20 m高度处偏差为20.6 mm，而最大偏差达到了28.3 mm。随着桥墩高度的持续增高，偏差和最大偏差之间的误差持续增大，当桥墩修建高度达到50 m时，误差达到最大的85.2%，此时的偏差和最大偏差相去甚远。50 m处的偏差仅为6.3 mm，若该桥墩修建高度仅为50 m，此时传统方法测量的桥墩垂直度符合规范要求，实际上最大偏差已经明显超出规范规定数值。全站仪测量桥墩垂直度不能确定最大偏差，所测得的结果不能反映桥墩的真实垂直度。相反，利用三维激光扫描技术获得桥墩点云，从全局出发测量桥墩垂直度更加科学合理。

4 结论

三维激光扫描技术可以获得桥墩结构三维几何信息，抓住矩形薄壁桥墩结构几何特性强的特点，提出了基于激光点云分析桥墩垂直度问题的方法，并根据数据关系得到以下结论：

1)垂直度偏差随桥墩高度的增高而增大，并最终呈现偏差不稳定的状态。

2)桥墩偏差在横桥(矩形桥墩的长边)方向上变化幅度不大且偏差小，在顺桥(矩形桥墩的短边)方向上的偏差变化幅度大且偏差大。对于矩形桥墩的施工，顺桥方向上的测量观察更为重要。

3)对于矩形桥墩而言，桥墩的倾斜大致沿着矩形桥墩某条对角线方向。在桥墩修建过程中应重点加强对角线方向上的观测。

4)桥墩特征点水平偏差最大处不一定是桥墩垂直度最大处，且最大水平偏差的出现是随机的，不可预测的，故采用全站仪单点测量桥墩垂直度得出的结果准确性不足。

5)本方法全方位呈现桥墩的三维空间状态，准确计算最大偏差并定位最大偏差所处的位置，对工程施工和测量起到了重要的指导意义。