基于多种障碍环境建模的机器人路径规划

陈岳军，王敬贤

(上海五零盛同信息科技有限公司，上海 200333)

智能化机器人拥有感知决策能力，它们可以辨识身边的信息情况，实现自主控制并完成复杂的任务[1]。机器人的路径规划问题是智能控制领域中的一个关键问题，保证机器人在完成任务的同时提高效率[2]。路径规划是在起始点和目标点之间选出一条最短路径，既能使机器人在行进过程中躲过障碍物，并且满足特定评价标准，如行走路线距离最短、到达目标行走时间最短、自身能量消耗最小等[3-4]。目前，机器人及其路径规划相关问题已经取得了许多成果，可分为传统方法和智能化方法两大类。

传统路径规划方法主要有几何构造方法和人工势场法。基于几何构造的方法将机器人抽象成一个可忽略的点，同时适当扩大障碍物体积，然后构造自由空间，并将其全部连通，最后采用图搜索算法找出最优路径[5]。人工势场法运用较为成熟，它用引力场和斥力场模型来表示机器人所工作的环境信息[6]，受力如图1所示。该算法原理简单，适合底层的简单控制，其运行速度和存储空间与其他算法相比具有优势。但它只解决局部空间内的避障问题，更适用于动态环境，在实时避障方面发挥重要作用。

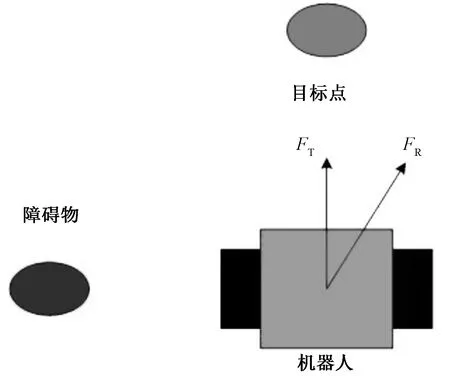
图1 人工势场法受力示意图

智能化路径规划方法主要基于遗传算法、模糊逻辑和蚁群算法。遗传算法在全局环境中搜索最优路径的能力比较强，有并行计算特性，应用较为广泛[7]。孙树栋等[8]实现了离散空间下机器人的路径规划，使用插入和删除算子，使规划出的路径是连续的。周明等[9]提出连续空间下机器人的路径规划。该方法简单可行，在执行过程中不会产生无效路径，但是对于复杂环境是不适用的。闫雪超等[10]提出一种用于机器人路径规划的改进遗传算法，解决过早收敛和随机变异等问题。模糊逻辑算法是一种常用的在线规划路径方法，依靠传感器的实时反馈信息，包含了人的操作经验和控制策略，将这些表示成模糊条件语句并构成一个集合[11]。该算法通过对环境信息的模糊化解决传统算法中机器人定位精度高的问题。郭娜等[12]针对机器人在复杂环境的局部死锁和路径冗余问题,使用结合预测和模糊控制的局部路径规划方法。该算法随着障碍物数目的增多，计算越来越复杂，而且在未知的动态环境中，模糊规则很难制定。

蚁群优化(ACO)算法是一种启发于蚁群觅食行为的智能仿生算法[13]。它利用一种称为信息素的特殊化学物质在个体和环境之间进行交流。刘煊琨等[14]将蚁群算法用于变电站路径的优化问题,。邓新文等[15]提出了一种基于蚁群算法的航迹规划方法，确保远程鱼雷航渡过程中避障的同时选择最优航行路径。现针对环境简单、障碍物分布较少的情况，采用人工势场法进行规划路径，当环境变得复杂，障碍物数量较多且较为密集时使用蚁群算法，为了验证这个方案是否可行，进行了两种算法的模拟实验并得到不同障碍物环境下的实验结果。

1 环境建模

为了使计算机能够辨识所要规划的环境，必须经过环境建模这一重要环节。环境建模选用的方法关系到整个路径规划的难易程度以及精确程度，合理的建模方式能使路径搜索量减少。机器人所处的环境因素以及障碍物信息情况等都是影响规划建模方法的因素。要做的工作就是将机器人所在的物理空间映射为算法可以处理的数学矩阵，最后再用环境模型将规划的结果表达出来。

1.1 栅格法环境建模

栅格法是目前在各领域应用都较成功的建模方法[16]。采用此方法是为了得到一张数字地图，起止点和障碍物信息都存储在这张地图中，最后规划出的路径也会展示在这张地图上。

该方法将一个二维工作平面划分成大小相同的栅格，每个栅格都具有一个0或1表示的二值信息。栅格大小选取是影响机器人运行性能的重要因素之一，它与环境信息的表达程度关系密切，也会对规划时间产生影响。栅格越小，环境信息描述越准确，但存储空间会相应加大，算法搜索范围也会加大，导致路径搜索时间变长。栅格越大，环境信息的表达误差越大，虽然决策速度变快，但路径规划不精确，可能会出现摩擦甚至碰撞障碍物的情形。因此在选择栅格大小时，应考虑到工作环境、障碍物信息以及实验结果精确度等多个问题。

在进行栅格法建模前，需要对环境信息预处理，在此遵循以下原则：①如果相邻的两个障碍物挨得特别近，则将它们看作一个障碍物处理；②工作空间静态障碍物数量大小已知，当障碍物不规则时，即边界不足一个栅格大小时，按一个栅格处理，这样做都是为了避免发生和障碍物的摩擦。

1.2 栅格环境转换为数学矩阵

将机器人工作的二维平面分成大小相等的栅格，综合考虑空间和障碍物数量两方面，取20×20空间大小。使用直角坐标系表示整个栅格平面，将栅格阵左下角的点作为原点，水平向右为横轴正方向，竖直向上为纵轴正方向。此时平面中每一个交叉点都能用坐标系中的对应坐标来表示，从(0，0)到(20,20)。

在机器人工作平面上，每个栅格有两种状态，障碍物空间和机器人自由行走空间，把涂黑的栅格表示为障碍物空间，把空白区域看作机器人可自由行走的空间。然后对栅格环境进行编码，采用二值编码方法，用1表示障碍物空间，用0表示自由空间，这样每一个栅格都能对应0或1。用此方法，当环境情况突变时只要改变数学矩阵中的值即可。此时，工作空间用数学矩阵的形式表示出来，工作环境的栅格模型和矩阵如图2所示。

图2 工作环境栅格模型和矩阵表示

2 人工势场法和蚁群算法实现

2.1 人工势场法的实现

人工势场法是一种人为设定的模拟虚拟力的算法，使机器人在由目标位置和障碍物组成的抽象势场中受到合力作用而运动。将目标位置视为引力场，其方向指向目标点，而障碍物视为斥力场，其方向指向远离障碍物的方向，两个场共同作用构造人工势场。在构建的人工势场中，机器人可以沿合成的势场运动，避开障碍物，向目标位置前进，从而走出一条无碰路径。

设机器人所在位置为qrobot=[x,y]T，目标位置为qgoal=[x1,y1]T，第i个障碍物的位置为qzhang(i)=[x2,y2]T。则机器人所在位置的引力势场为

(1)

引力为

Fyin=kyin(qrobot-qgogal)

(2)

机器人所在位置的斥力势场为

(3)

斥力为

Fchi=-Uchi

(4)

式中：kyin表示引力的比例系数;kchi表示斥力的比例系数;(qrobot-qgogal)表示机器人当前所在位置与目标点的距离;p(q)表示机器人与障碍物的最短距离。

具体实现步骤如下：

1)参数初始化，给定位置信息和各系数。

2)循环执行人工势场法的主功能。依次调用计算角度的子功能、计算引力的子功能、计算斥力的子功能，进行各个关键量的计算。

3)计算机器人的下一步位置并保存。

4)循环执行以上步骤，直至机器人到达目标点，并用变量K记录迭代的次数。

2.2 蚁群算法的工作原理

蚁群算法是通过模拟自然界中蚂蚁群体的觅食过程而得出的。当蚂蚁遇到一个不曾走过的路口时，随机选择一条路径前进，同时留下供交流的信息素，蚂蚁所走路径越短且走过数量越多，释放信息素会越多，作为后续蚂蚁选择路径的依据。哪条路径最优，选择的蚂蚁会越多，此路径信息量越大，即信息正反馈现象。而其他路信息素会随时间而挥发，循环执行得到一个最优解。

如图3所示，AE之间可以有两条路径供选择，其中AB=DE=HD=HB=1，BC=CD=0.5，假设原路不存在信息素，每只蚂蚁前进速度一样，单位时间内走长度为1，且释放相等浓度的信息素。当t=0时，从A、E两点各有30只蚂蚁同时出发。当t=1时，蚂蚁从A到B，这时BH与BC信息素浓度相等，则蚂蚁随机二选一前进，会有一半蚂蚁选择BH较长路径，另一半选择BC较短路径。同时，从E点蚂蚁走到D点，各一半蚂蚁分别选择DH和DC。当t=2 时，选择BC与DC的蚂蚁分别通过BCD和DCB，可选择BH与DH的蚂蚁此时只走到H。此时BCD走过的蚂蚁数量是BHD的两倍，则路径BCD上总信息素浓度相比于BHD是它的两倍，以后若再有蚂蚁在路口选择时，就会向信息素浓度高的路径前进。这个过程循环进行，选择短路径的蚂蚁数量越来越多，此路径信息素浓度也增大，最终趋于最优解。

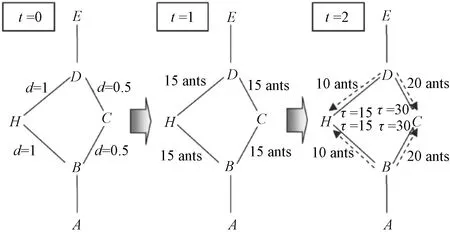
图3 蚁群算法原理示意图

2.3 蚁群算法的数学抽象

1)对蚂蚁个体的抽象。每只蚂蚁看作一个简单智能体，可根据局部环境构造候选解，也能进行信息交流。

2)寻找路径的抽象。用栅格两顶点作为蚂蚁巢穴(起始点)和食物所在地(目标点)，蚂蚁觅食过程看作算法求解过程，图轨迹作为信息素信息，比较相邻节点轨迹浓度来决定下一步走向。

3)信息素挥发的抽象。将信息素挥发过程离散化，规定经过一个单位时间信息素挥发一次，若用ρ表示信息素挥发系数，则1-ρ表示信息素残留因子，在每时刻记录各条路径的信息素情况。

4)启发因子的引入。蚂蚁行走路径的概率问题是一个随机搜索过程，引入启发因子表示蚂蚁从一个节点转移到另一节点的期望概率，有引导作用，使寻优路径时间变短，增加时效性。

通过以上抽象可以将蚁群觅食问题转化为数学模型。蚂蚁个体是算法基本对象，所选路径取决于拥有的知识，而知识来源于信息交流及环境感知，具有自学习能力，可根据环境变化和以往经验对知识结构更新，实现算法逐步优化。该算法流程如图4所示。

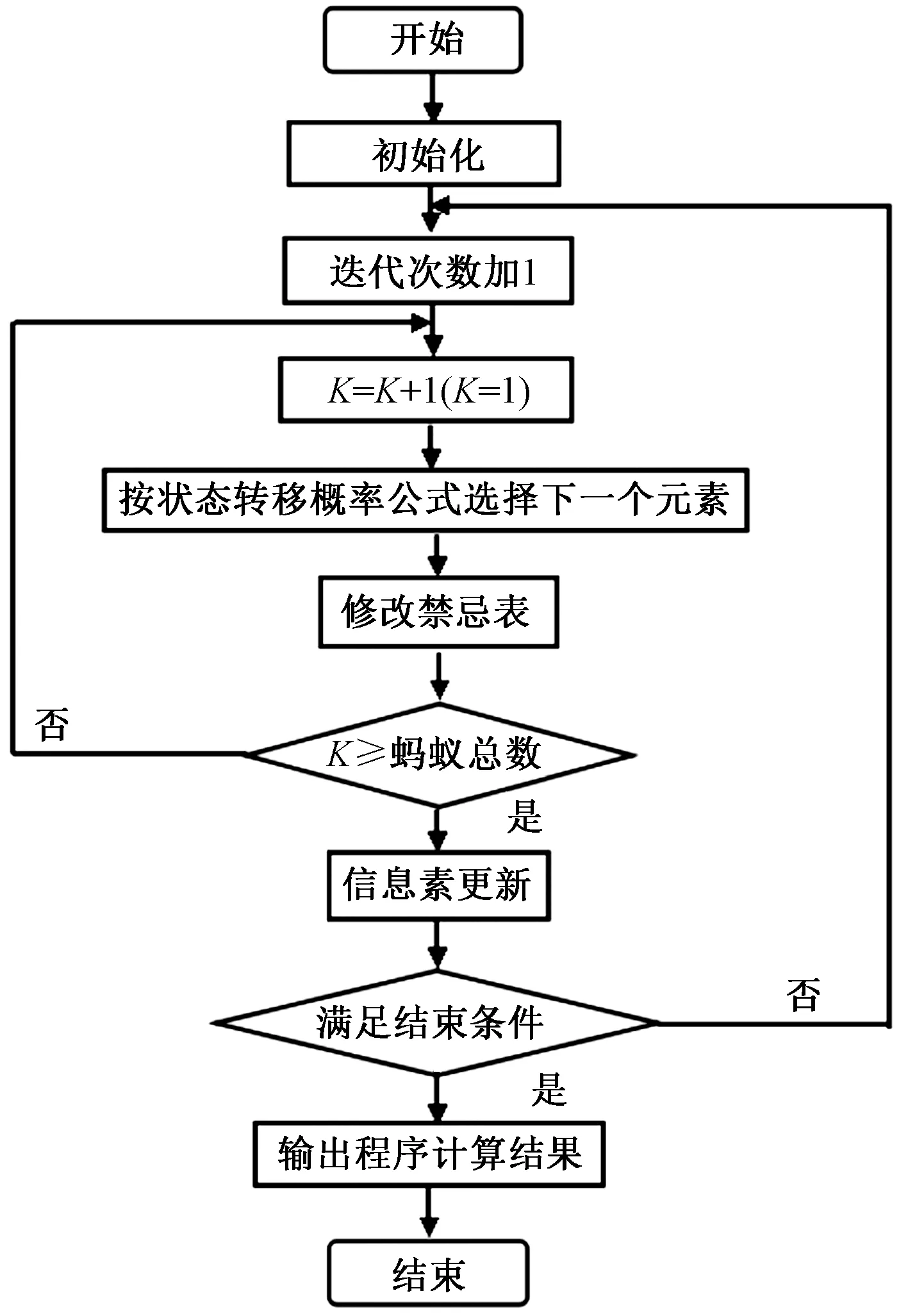
图4 蚁群算法流程图

2.4 蚁群算法模拟流程

1)工作环境用0和1组成的矩阵表示。

2)输入初始信息素信息，选择起止点。在本算法设计时，要设置各种参数如表1所示。初始状态蚂蚁在出发点S，需将初始点放到禁忌表中。

表1 算法基本参数设置

3)选择下一步节点时，各节点的概率由该节点的信息素求出，计算公式如式(5)所示。其中，πij(t)为图中弧(i,j)上残留的信息素浓度；ηij为与弧(i,j)相关的启发式信息；α、β分别为πij(t)、ηij的权重参数。

(5)

当蚂蚁转移时，总按理论计算结果进行容易很快陷入收敛。为避免此问题，引入轮盘算法[17]，选择节点j并将其加入禁忌表即可。轮盘赌算法将圆盘分成n份，每个扇形面积不同，转动圆盘并稳定后，选择参照点所在扇形即可。当扇形所占的面积越大，则参照点落入其区域概率越大，在蚁群算法中相当于设定该节点被选择的概率也越大。

4)更新路径以及路程长度并实时记录。

5)重复3)、4)过程，直到到达目的地。

6)重复3)、5)，直到某一代蚂蚁迭代结束。

7)更新信息素矩阵，经过时间Δt后，各条路径上的信息素按式(6)进行调整。

πij(t+1)=(1-ρ)πij(t)+Δπij

(6)

式中：ρ为信息素挥发系数；1-ρ为信息素残留的系数；ρ⊂[0,1)使信息素不至于无限积累；Δπij(t)表示在时间的增量中，蚂蚁所走路径上信息素的增加量，初始时刻Δπij(0)=0，求解公式为

(7)

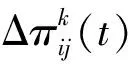
根据信息素更新方式的差别，有

(8)

式中：Q为信息素强度；Lk表示第k只蚂蚁所走路径长度。想要一波蚂蚁到达目标点后，才更新路径上的信息素浓度，而这个模型利用的正是整体信息，因此在本文中采用此模型。

8)迭代3)～7)到n代蚂蚁迭代全部结束。

3 模拟实验与结果

3.1 实验说明

为对两种算法进行比较，并在不同环境中验证算法有效性，进行路径规划模拟实验。

1)人工势场法模拟。主函数功能为迭代过程的主体。计算斥力的子功能可计算出斥力在x、y方向的数组分量。计算角度的子功能用于计算车、障碍物和目标之间的与X轴之间的夹角。计算引力的子功能可计算出目标对车的引力在x、y方向的两个分量值。

2)蚁群算法模拟。首先要建立栅格环境，然后模拟蚁群算法的完整过程，在这个算法内部包含觅食规则、选择节点规则、避障规则、信息素更新规则等。

3.2 人工势场法的仿真及结果

在这个实验中，主要改变障碍物个数和位置分布，通过在几种不同障碍物环境的模拟结果分析人工势场法优点和局限性以及适用环境。

1)当空间有一个障碍物时，结果如图5所示，两种环境中的迭代次数分别为K=107和K=114。

图5 障碍物个数n=1时仿真结果

从图5可看出，当环境中有一个障碍物时，机器人可通过构造的人工势场躲避障碍物，并沿最短路径寻找目标，即使改变障碍物位置，依然可得到良好结果，因此人工势场法用于简单环境是可靠的。

2)当空间中有两个障碍物时，结果如图6所示，迭代次数均为K=109。

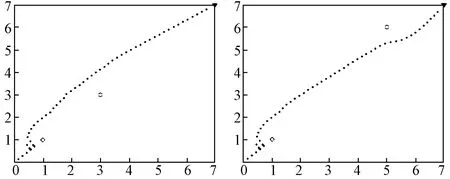
图6 障碍物个数n=2时的仿真结果

从图6可看出，当存在两个障碍物时，机器人可通过合力作用成功躲避障碍物，并沿最短路径到达目标点，改变障碍物的位置结果依然满意。

3)当空间中有3个障碍物时，结果如图7所示，迭代次数分别为K=110和K=52。

从图7可看出，一种情况机器人连续躲避了两个障碍物，然后沿最短路径向目标点前进；第二种情况，机器人从两障碍物之间穿过，也取得不错效果。3个障碍物环境人工势场法可完成规划任务。

图7 障碍物个数n=3时的仿真结果

4)当空间中有4个障碍物时，结果如图8所示，迭代次数分别为K=56和K=51。

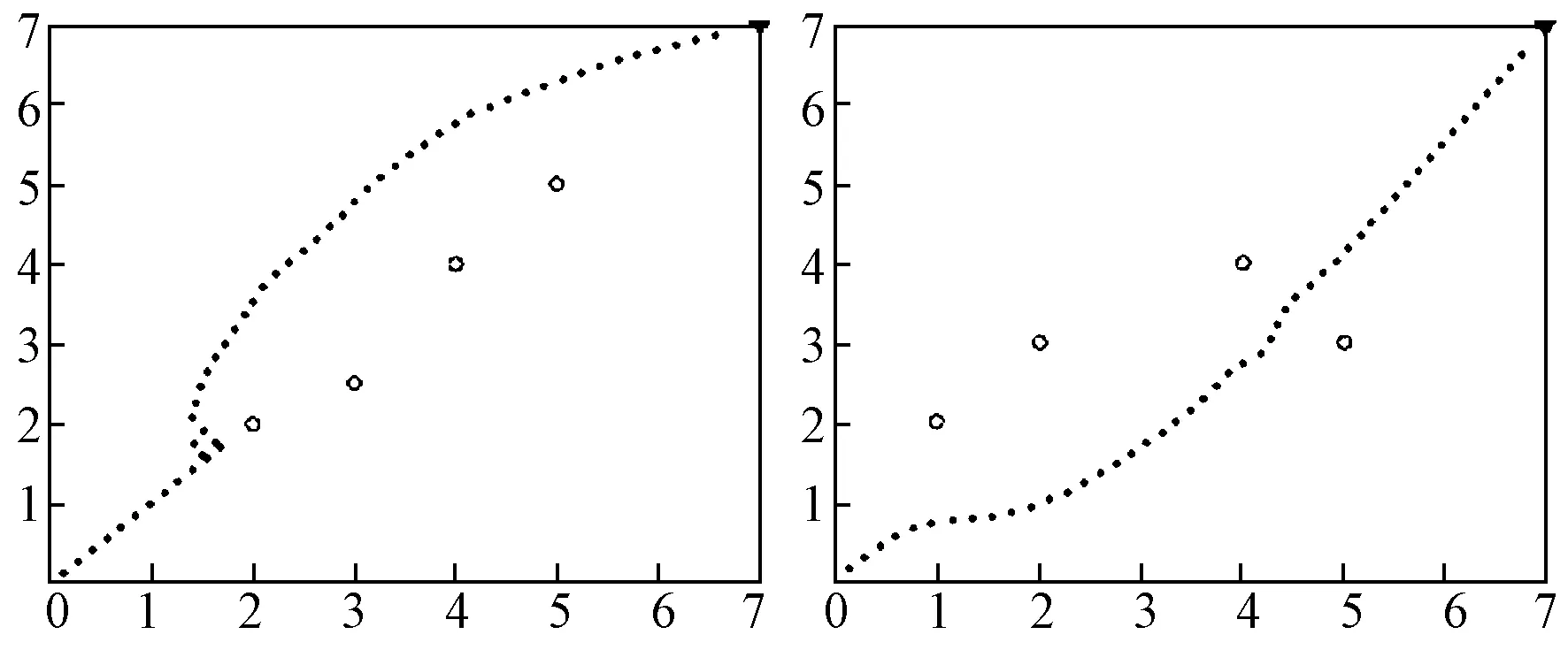
图8 障碍物个数n=4时仿真结果

这种情况和3个障碍物环境中的仿真结果相似，均能躲避障碍物。但此时可观察到两种环境下规划的路径显然已不是最短路径，这是合力方向不当造成的。

5)当空间中有5个障碍物时，结果如图9所示，迭代次数分别为K=121、K=113和K=52。

图9 n=5时两种不同情况仿真结果

从图9(a)看确实避开了障碍物，但最后机器人不能到达目标点，这是由于障碍物和目标点距离较近，目标在障碍物影响范围之内，这时斥力大于引力，停止点位置两者相等造成的。从图9(b)在机器人行进过程中，躲避第4个障碍物时出现问题。观察这个位置特征，可看出这是个特殊位置，此时，机器人、障碍物和目标点在同一条直线上，这时合力也是沿着这条直线，才导致了这个问题。因此在这种情况下，人工势场法已不能完成基本规划任务。

通过比较这5种不同障碍物环境下的仿真可以发现，当障碍物数量较少且分散时，人工势场法可规划出满意路径，且该路径为平滑曲线。当障碍物数量较多时，特别是障碍物分布在目标点周围或出现机器人、障碍物和目标点三者在同一条直线上的情况，该算法已不能规划出较优路径。基于这种局限性，须使用智能化算法中的蚁群算法进行复杂环境中的路径规划。

3.3 蚁群算法的仿真及结果

3.3.1 参数的设置及初始化

蚁群算法中各参数值会影响算法的性能，研究下列参数最佳组合是有必要的。①M：蚂蚁数，即每波有M只蚂蚁觅食；②ρ：信息素蒸发系数；③β：表征启发式因子的重要程度。

3.3.1.1 蚁群规模的设置

一只蚂蚁所走路径为整体解集中的一个，M只蚂蚁在一次迭代过程中所走路径为整体解集中一个子集。蚁群数量适当增多可使规划出来的路径结果更稳定和更准确，但蚂蚁数量过大时，算法需要耗费过长时间；反之，当蚂蚁数量过少时，会降低算法的随机性，导致过快收敛，计算结果不可靠。以下通过在不同数量蚂蚁的情况下进行实验，通过实验结果来直接得到算法中蚂蚁数量的最佳设置值。M=10、30、50、70、90时，路径规划和收敛曲线如图10所示。

图10 改变蚂蚁数量时的仿真图像

对比图10可知，当蚂蚁数量M=50时，路径长度最短，也不至于陷入过早收敛，因此将蚂蚁数量设为M=50。

3.3.1.2 信息素蒸发系数ρ的取值

ρ取值会对算法搜索能力和收敛速度产生影响，ρ太小，信息素蒸发少残留多，结果不具随机性；ρ增大，结果具有普遍性，但算法收敛慢，时效性较差。以下通过实验验证算法中ρ的最佳设置值。

当ρ=0.1、0.2、0.3、0.4、0.5时，蚂蚁的最短路径图和收敛曲线如图11所示。

图11 改变信息素蒸发系数时的仿真图像

可以看出，ρ=0.3时，路径长度最短，最终稳定时的迭代次数也最小，因此取信息素蒸发系数ρ=0.3。

3.3.1.3 启发式因子重要程度β的设置

启发式因子β表示蚂蚁在寻找路径过程中所积累的信息量是对于它作出选择的重要程度，值越大，会越多重复以前选择，失去随机性，使结果过早收敛。通过在β不同取值情况下实验结果来直接得到算法中β的最佳设置值。

当β=1、3、5、7、9时，蚂蚁的最短路径图和收敛曲线如图12所示。

图12 改变启发式因子时的仿真图像

从图12可以看出，当启发式因子很小时，不能找到最优路径，当启发式因子逐渐增大时，路径长度逐渐变小，迭代次数变小，但当启发式因子过大时，蚂蚁在路径选择上可能会过早陷入收敛。因此当启发式因子β=7时，可规划出最有路径。

3.3.2 不同障碍物空间的仿真结果

在3.3.1节中可以看到，当蚂蚁数量M=50、信息素蒸发系数ρ=0.3、启发式因子β=7时，可规划出最优路径。只有在不同障碍物环境下都能规划出满意结果才能说明算法的有效性和参数选择合理性。

1)障碍物环境1仿真如图13所示。从图13中可以看出蚂蚁行走的路径为无碰路径，由蚂蚁路径规划的收敛曲线可以得知当迭代次数为52时可得到收敛解，路径长度已趋于稳定值且为最小值。

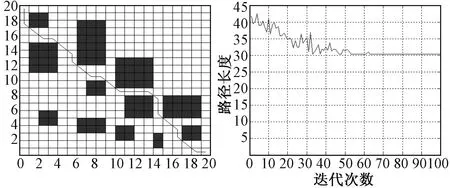
图13 障碍物环境1中最优路径和收敛曲线

2)障碍物环境2中仿真如图14所示。由蚂蚁爬行过程中所经过的最短路径图可看出，显然为无碰路径，由蚂蚁路径规划的收敛曲线可以得知到第52代蚂蚁可得到稳定解。

图14 障碍物环境2中最优路径和收敛曲线

4 结论

通过不同障碍物、不同参数下的实验得出：

1)当障碍物数量较少且分散时，人工势场法可以规划出满意的路径，且该路径为平滑的曲线。该算法所占空间少，运行速度和路径的收敛速度都较快，但有它的局限性，容易使系统陷入局部极值。当障碍物数量较多时，特别是障碍物分布在目标点周围或出现机器人、障碍物和目标点三者在同一条直线上的情况，使用简单的人工势场法已不能规划出较优路径。

2)基于人工势场法的这种局限性，使用蚁群算法在复杂障碍物环境中的实验结果表明，将蚁群算法用于复杂环境下的路径规划问题是可行的且本文参数的选取是合理的。此外，在仿真过程中研究蚂蚁数量M、信息素蒸发系数ρ和启发式因子重要程度β等参数的最佳组合是很重要的，这些参数会影响规划路径的长度和收敛速度，通过多次模拟结果的对比实验来决定算法中的最佳参数设置能得到更为优化的结果。