基于RNG k-ε湍流模型的串列双矩形截面桥墩绕流流场特性研究

丁安娜

(铅山县水利局，江西 上饶 334599)

随着中国经济和交通运输行业的快速发展，越来越多的跨江、跨海桥梁被修建，对江河两岸人员通行、文化交流和物资运输等起到了重要作用[1-2]。据统计，截至2019年中国公路大型桥梁数量多达10.8万座，对推动区域经济发展起着显著作用[3]。然而，涉河桥梁的建设将影响河流的度汛安全，对桥墩周围流体流动、河床阻力及船舶航行等造成不利影响[4]。《中华人民共和国防洪法》规定，涉河项目建设应符合防洪标准，不得危害堤防安全、影响河势稳定、妨碍行洪畅通等相关内容[5-6]。因此，研究桥墩绕流流场结构特征对优化桥墩布设、保障船舶安全航行等具有重要意义。

大量学者对桥墩绕流开展了大量物理实验与数值模拟等研究。叶玉康等[7]开展了串列双圆柱桥墩绕流流场特性的数值模拟研究，分析了不同桥墩间距对桥墩周围涡量分布和横向流速的影响。田正野等[8]采用大涡模拟分析了串列多圆柱桥墩绕流特征，获得了圆柱桥墩绕流的压力云图、瞬时流速和涡量图等。童晓剑[9]开展了低雷诺数条件下多圆柱桥墩绕流流动特性，分析了桥墩排列方式、间距和直径比对圆柱桥墩绕流流动特性的影响。余攀登等[10]以海底悬跨管道为研究背景，分析了高雷诺数下近壁圆柱的绕流特征。高鹏程等[11]研究了圆端形桥墩周围流体的行进水流及其流场变化，探索了圆端形桥墩绕流与冲刷之间的关系。此外，李鹤高、魏彭林等[12-13]对桥墩周围紊流区宽度进行了研究。综上，目前大部分学者主要研究的是单桥墩绕流，尤其是圆柱绕流，有少数学者对多圆柱桥墩绕流进行了研究。据有关学者对长江流域上89座桥梁桥墩截面形状的统计结果，水中无桥墩和为斜拉桥异形墩分别占23%、41%，圆端形截面墩、矩形截面墩和圆形截面墩分别占10%、11%、3%[14]。矩形截面桥墩因采用现浇和模板拼装施工，施工速度快，从而在桥梁工程中被广泛采用。因此，本文以多矩形截面桥墩实际工程为研究背景，采用Fluent软件对单矩形截面桥墩和串列双矩形截面桥墩绕流流场进行数值模拟计算，分析不同桥墩间距工况下串列双矩形桥墩绕流流场分布特征。

1 数值计算模型

a)模型的建立。以忠州长江大桥为实例建立模型，该桥梁桥墩采用矩形薄壁空心墩，截面尺寸为6 000 mm×4 000 mm，属于中等尺度桥墩。为提高模型计算速度，采用1∶50缩尺比进行模型建立，缩尺后矩形桥墩尺寸(长和宽分别用H、W表示为：H×W=120 mm×80 mm。图1所示，整个模型计算域尺寸为：40W×20W，即3 200 mm×1 600 mm，桥墩前侧为流体入口，后侧为出口。为充分研究水流经过不同间距桥墩后的流动特征，第一个桥墩中心距流体入口10W，距流体出口30W；顺着水流流动方法看，定义桥墩的左侧区域和右侧区域分别为桥墩左侧和右侧，且桥墩中心距两侧边界均为10W。

图1 数值计算模型网格划分

b)计算工况。数值模拟重点研究流体绕桥墩流动状况，流体经过桥墩后流向发生改变，流线会出现严重弯曲。因此，控制方程采用重整化的RNG k-ɛ双方程湍流模型，该模型在求解高弯曲程度和高应变率的流体流动时具有更高的计算精度、更好的求解稳定性和更快的求解速度等，大量学者已采用该模型求解桥墩绕流问题[3,15-17]。数值计算控制方程的具体参数参照叶玉康等[7]的研究成果。计算域入口流体流速设定为恒值，其大小为0.4 m/s，方向沿x轴正向。论文研究重点是不同间距矩形截面桥墩绕流的流场特性，因此桥墩间距L设置了L/W=0、2、4和6四种工况，其中间距L是指第二个桥墩前壁至第一个桥墩后壁的距离，L/W=0是指单个矩形截面桥墩绕流工况。

c)计算网格和边界条件。图1所示，模型利用ICEM软件进行结构化四边形网格划分。为更好捕捉桥墩周围绕流流场细节，尤其是尾流流场特性，对计算域桥墩中心线附近区域进行了局部加密细化处理；此外，为提高计算精度，对桥墩周围网格进行进一步加密处理，计算模型网格总数量约为9.2万。模型边界条件设置如下：计算域前侧设置为速度入口，为0.4 m/s；后侧设置为压力出口，为101 000 Pa；桥墩壁为无滑移壁面，计算域左右两侧边界设置为对称边界。模型采用非稳态瞬时计算方法，总计算时间为30 s。

2 串列双矩形截面桥墩绕流流场特性

2.1 矩形截面桥墩与常规圆柱形桥墩绕流流场对比分析

图2显示了矩形截面桥墩绕流特征与常规圆柱桥墩的对比结果。圆柱桥墩绕流结果为叶玉康等[7]开展的双圆柱桥墩数值模拟结果。由图可知，在两桥墩间距相近条件下，矩形截面桥墩绕流流动更复杂，其桥墩尾流涡体尺寸更大，涡体及流线弯曲区横向分布范围更广；从横向流速时程曲线分布可知，圆柱桥墩绕流横向流速波形图形态单一且呈对称分布，但矩形桥墩绕流横向流速波形图周期内出现局部波动，波形图形态复杂，且横向流速峰值更大。总体而言，矩形截面桥墩因其排导性差，对来流干扰程度大，较常规圆柱桥墩绕流运动更复杂。因此，十分有必要研究矩形截面桥墩布置参数对其绕流流场特征的影响。

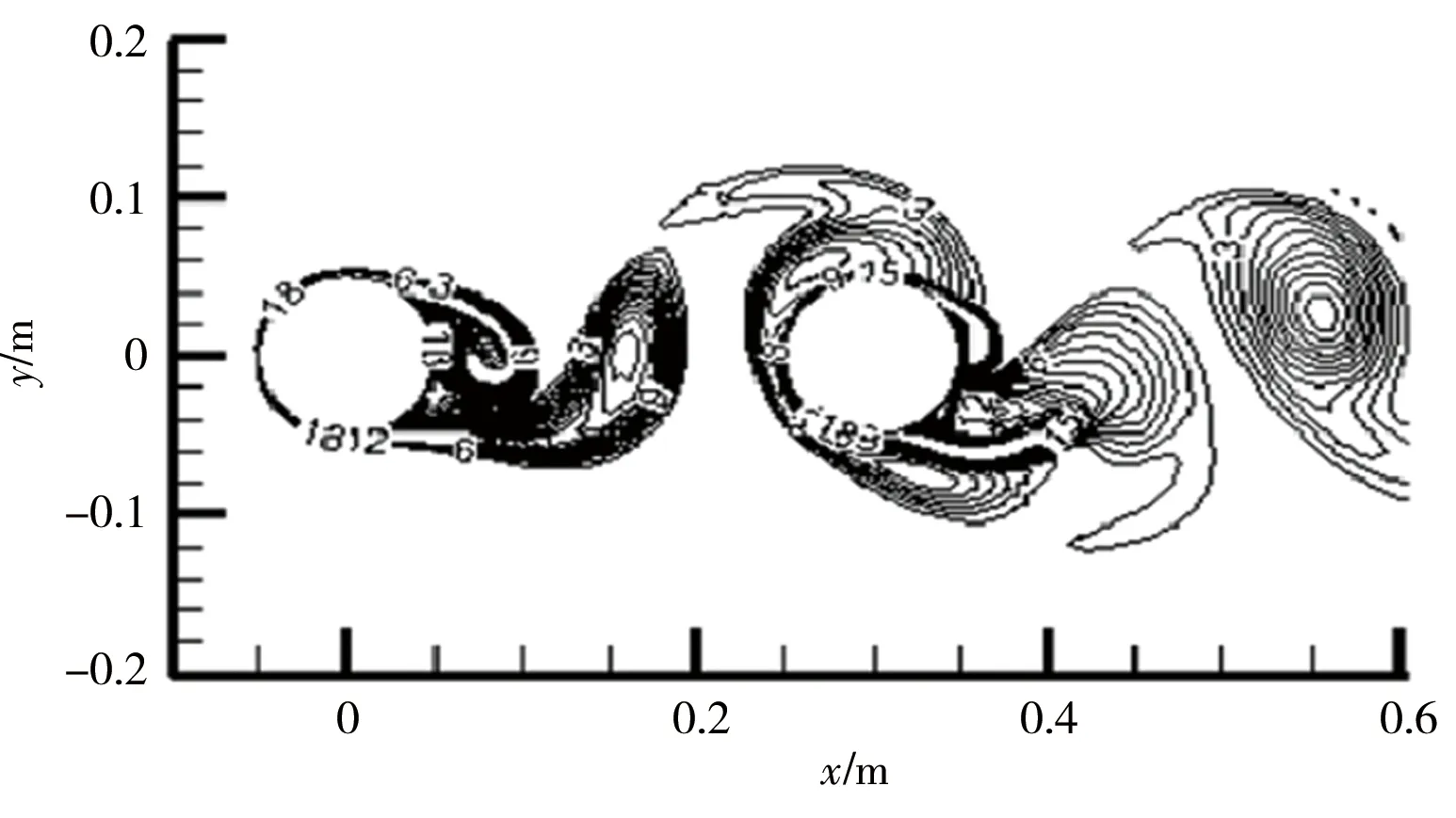
a)圆柱桥墩涡量等值线

2.2 涡量分布

图3显示了不同间距条件下矩形截面桥墩尾流涡量等值线。由图可知，与单矩形截面桥墩绕流相比，串列双矩形截面桥墩尾流流动更加复杂，且流动状态与桥墩间距紧密相关。当L/W=0时，即单桥墩工况，流体经过矩形截面桥墩后，其尾流出现了卡门涡街现象，并在距桥墩不同距离下游处形成了多个涡体，涡体形态、尺寸等分布具有较强的规律性。对串列双矩形截面桥墩而言，当L/W=2时，尾流的涡量等值线分布较单矩形桥墩更为复杂，但由于两桥墩间的距离不足以让涡体在两桥墩间充分发展，涡体只在第二个桥墩尾流中形成。图3b所示，第一个桥墩SL1侧剪切层分离后重附在第二个桥墩剪切层上，而SL2侧剪切层将直接掺混到第二个桥墩尾流旋涡中；此外，串列双矩形截面桥墩尾流旋涡的横向分布范围也将明显扩大，单桥墩和串列双矩形桥墩涡体横向分布范围分别为5.6W、8.0W。当L/W≥4时，第一个矩形桥墩两侧剪切层不再附着在第二个桥墩剪切层上，每个桥墩后尾流都会形成卡门涡街，并在第一个矩形桥墩尾流旋涡干扰下，第二个矩形桥段尾流流动变得更加不稳定，涡体之间相互附着，涡量强度也随之增大，涡量等值线分布密度加密。

a)L/W=0

2.3 流线及压力分布

图4为t=30 s时不同间距条件下矩形截面桥墩绕流流线分布。流体在桥墩前方区域流动十分稳定，流体流速几乎相同，且流线之间相互平行(图4中红色箭头所示)。当流体经过矩形截面桥墩时，桥墩迎面流体将从两侧绕行，桥墩前壁流体流线将严重弯曲，流体流向发生改变。桥墩使流体过流断面积减小，在桥墩两侧的流体流速将增加(如桥墩两侧红色流线区域)，且流线分布更密。桥墩尾流由于涡体的产生，在涡体区域流体流线将严重翻转和弯曲，且流体流速较低，为低速区(如桥墩尾流绿色流线分布区域)。由图4可知，矩形截面桥墩间距对流线分布具有重要影响。单矩形截面桥墩绕流流线分布和常规圆柱形桥墩绕流情况类似(图4a)。当桥墩间距L/W≤2时(图4b)，第一个桥墩尾流弯曲的流线与第二个桥墩相遇，从桥墩两侧绕流，并在两侧形成速度增加区域；第二个桥墩尾流流线分布与单桥墩尾流流线分布类似，但流线弯曲程度更严重，且弯曲流线的横向分布区域更广。当桥墩间距L/W≥4时(图4c—4d))，两桥墩间也将出现流线弯曲区域，其余流线分布特征与L/W≤2时较为类似。

a)L/W=0

在t=30 s时，不同间距串列双矩形截面桥墩绕流压力分布见图5。在第一个矩形截面桥墩前形成了压力增高区(红色区域)，而桥墩两侧和后方为压力降低区(绿色和蓝色区域)。结合图4可知，其主要原因为：根据伯努利方程，由于桥墩使流体过流面积缩小，桥墩前方流体形成驻流，流速降低且流向发生改变，且两侧流速增加，从而在桥墩前方和其他方向分别形成压力增加区和压力降低区。此外，串列双矩形截面桥墩尾流流动更加复杂，低压区分布范围更广，且流动状态与桥墩间距紧密相关。当桥墩间距L/W≤2时，两桥墩间全为压力降低区，第二个桥墩尾流形成了多个压力降低区。当桥墩间距L/W≥4时，在第一个桥墩后方除形成压力降低区外，在第二个桥墩前方还形成了局部压力增高区，但压力值较第一个桥墩前方更小。

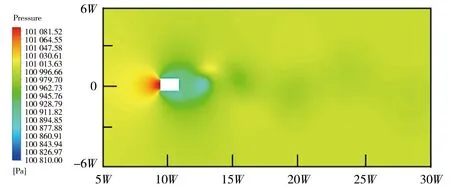
a)L/W=0

2.4 横向流速分布

由桥墩绕流流线及压力分布云图可知，流体在桥墩前方的计算域内沿x轴正向流动，当遇到桥墩时，桥墩壁前方形成驻流，随后沿桥墩两侧分离流动，并在桥墩后方汇流。因此，桥墩绕流将形成斜向流动，定义垂直于两桥墩中心线方向的流体流速为横向流速。图6显示了不同间距串列双矩形截面桥墩绕流横向流线分布云图，桥墩间距分别为L/W=0，2，4，6。由图6可知，第一个矩形截面桥墩前方两侧形成了对称分布的正负横向流速区。对单桥墩绕流而言(即L/W=0)，桥墩后方尾流横向流速在不同距离处呈正负交替分布(图6中黄色和蓝色区域)，主要是由桥墩尾流交替分布的涡体不断生成、发展和溃灭所导致。对串列双矩形截面桥墩而言，两桥墩之间区域会出现正负横向流速区，且间距越小横向流速值越大，但正负横向流速分布区随着间距的增加而增多。第二个矩形桥墩尾流横向流速分布规律与单桥墩较为类似，但串列双矩形截面桥墩绕流的正负横向流速值更高，且横向分布区范围更广。

a)L/W=0

桥墩绕流横向流速分布规律与船舶航行状态密切相关。为更好揭示桥墩绕流不同位置的横向流速分布规律，对桥墩周围不同时刻流体的横向流速进行观察，各观察点位置见图7。观察点a—h号位于距桥墩中心线1.25W测线上，其中b号点位于过第一个矩形桥墩中心的垂线上，其前方距离W处为a号点，后方按间距W和2W依次设置c—h号点；i、j号测点在b号上方，距桥墩中心线距离分别为2W、3W；o、p号测点在h号上方，距桥墩中心线距离分别为2W和3W。

图7 串列双矩形截面桥墩横向流速观察点位置

图8所示，从不同间距桥墩绕流在y=1.25W测线上各代表性测点(桥墩上游测点a号、第一个桥墩左侧测点b号、两桥墩间测点c、d号、桥墩下游测点g、h号)横向流速的时程曲线可知，各测点横向流速均出现周期性波动。第一个矩形桥墩左前方区域横向流速均为正值，如测点a、b号，且横向流速曲线波形呈对称分布。对单矩形截面桥墩而言(即L/W=0)，桥墩后方区域横向流速都在vy=0 m/s上下波动，波动范围为-0.2～0.2 m/s，且横向流速波形图为对称分布。对串列双矩形截面桥墩而言，第一个桥墩后方区域横向流速正负交替变化，且2个桥墩之间左侧区域横向流速正峰值略大于负峰值；第二个桥墩后方区域横向流速波形图不再对称，在曲线某一位置出现二次波动，这主要由第一个桥墩尾流涡体对第二个桥墩的冲击和干扰，以及第二个桥墩尾流涡体的脱落导致。此外，桥墩尾流横向流速波动峰值较单桥墩有所提高，尤其是正峰值，大部分达到了0.3 m/s，尤其是L/W=2工况中的d号测点，该点恰好位于第二桥墩左侧附近，该区域流体横向流速明显增加，正峰值达到0.5 m/s。

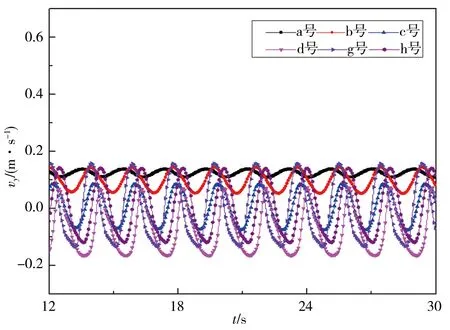
a)L/W=0

图9、10为距桥墩中心线不同距离处测点横向流速变化曲线，其中测点b、i、j号位于第一个桥墩左侧，测点h、o、p号位于第二个桥墩左后方。对单矩形桥墩和串列双矩形桥墩而言，b、i、j号测点横向流速波形图单一且对称分布，但串列双矩形桥墩绕流横向流速峰值更大；距离桥墩越远，测点横向流速波动峰值越小。对第二个桥墩左后方区域，横向流速波形图变得不对称，尤其对L/W=6工况而言，h、o、p号测点横向流速不再周期变化。总体上而言，距离桥墩中心线越远，横向流速越低。

a)L/W=0

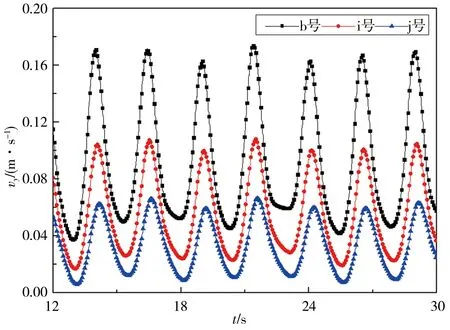
d)L/W=6

a)L/W=0

3 结论

本文建立了单矩形截面桥墩、串列双矩形截面桥墩绕流数值计算模型，采用RNG k-ɛ湍流模型进行非稳态瞬时求解，分析了不同桥墩间距工况下串列双矩形桥墩绕流流场特性，获得了涡量分布、流线及压力分布、横向流速分布等与桥墩间距的关系。主要结论如下。

a)与常规圆柱桥墩绕流相比，矩形截面桥墩绕流流动更复杂，尾流涡体尺寸更大，涡体及流线弯曲区横向分布范围更广，横向流速波形图形态复杂，且峰值更大。

b)串列双矩形截面桥墩尾流流动较单桥墩绕流更复杂，桥墩尾流涡体横向分布范围扩大，且流动状态与桥墩间距紧密相关。桥墩间距影响两侧桥墩剪切层的生成、分离和重附，当L/W≥4时上游桥墩尾流才形成涡体，否则只在下游桥墩尾流形成卡门涡街，伴随着涡体周期性地脱落。

c)流体遇桥墩时流线发生翻转、弯曲，桥墩两侧流速增加且流线分布加密，桥墩尾流形成多个流线弯曲的低速区；串列双矩形桥墩流线弯曲区分布范围更广，当L/W≥4时两桥墩间也形成流线弯曲区。上游桥墩前方和其他侧面区域分别为压力增高区和压力降低区，下游桥墩尾流形成多个压力降低区，而两桥墩间区域压力分布受桥墩间距影响。

d)上游桥墩前方出现呈对称分布的正负横向流速区，桥墩尾流横向流速沿水流方向呈正负交替分布；串列双矩形桥墩间距越大，桥墩间正负横向流速区分布越多，横向流速峰值越低。单桥墩绕流横向流速波形图单一且呈对称分布，串列双矩形桥墩时上游桥墩后方区域横向流速波形图不再对称分布，局部出现二次波动，且横向流速波动峰值较单桥墩增大，距离桥墩中心线越远波动峰值越低。