基于区域差异性的应急物流定位-路径问题研究

赵思晴，倪 静，曾凡龙

(上海理工大学 管理学院，上海 200093)

中国国土辽阔，地震、洪涝等自然灾害频发，带来巨大的人员伤亡以及财产损失。在灾难发生后，灾区往往在短时间内需要大量物品和医疗物资。如何在短时间内根据需求点的受灾情况，将需求物资根据需求分发到需求点，是降低灾区损失的必要条件之一。

目前，中外学者对应急物流过程中的选址分配问题和应急物资配送问题有一定的研究，并提出了应急物流的选址路径问题。刘长石等[1]在未定路网情景下综合考虑路网情况、时间窗等特性构建了一个以应急物资总配送时间最短为目标的灾后应急物资多方式配送的路径优化模型。Liu等[2]在物资需求量和受伤人口不确定条件下基于鲁棒理论以系统总成本最低建立了多目标路径选址模型。孙华丽等[3]考虑路径风险和物资需求量的不确定性，基于鲁棒优化理论，以最小化车辆最长配送时间和应急物流系统总成本，建立了双目标多物资定位路径优化模型。楼振凯[4]在考虑物流时效的基础上，综合考虑政府方的应急系统消耗总时间最少和企业面的总成本最低，构建了双层规划模型。王海军等[5]在允许拆分配送的策略下，建立了以平均车辆行驶时间和系统总成本为目标的开放式选址路径模型。Zhou等[6]以系统每阶段未满足需求和风险最低为目标函数构建了多目标优化模型，并且考虑了多阶段的动态物资调度，并运用多目标进化算法求解该模型。Najafi等[7]基于鲁棒理论以应急系统中未满足需求的物资最低、受伤人数最少以及使用车辆数量最低为目标函数，建立了多目标、多模式、多商品、多周期的随机模型，并根据层次目标函数进行求解。张雷[8]针对震后短时间内应急物资短缺的情况，利用可变集理论，确定受灾点应急物资的优先级，并以整个救援过程总耗时最低构建定位路径模型。Vahdani等[9]以系统成本低、时间短和链路通达性最大化为目标函数，构建了两阶段多商品模型，对配送中心和各级能力仓库的选址、仓库内储存货物的相关决策以及已建立的配送中心进行了协调。宋华英等[10]从灾民容忍度出发建立多周期、多物资模型，提出了动态物资配送模型。

从上述文献中可以看出，现今学者主要从应急系统总时间最短或整体成本最低出发，考虑系统的时效性；或考虑受灾点需求的确定性或不确定来考虑应急系统的需求情况；很少学者从受灾点的不同受害程度出发，对受灾点的受灾情况进行分析，考虑应急物资调运的定位路径问题。针对上述的研究不足，提出综合考虑区域差异性来构建应急物流的定位路径模型，关于区域差异性从受灾点优先级和集散点的反应能力两方面综合考虑，并且采用改进人工蜂群算法对模型进行求解。

1 模型结构

1.1 模型假设

自然灾难发生后，为了便于救援物资的及时中转，在需求点的附近，受灾影响较少并且交通便捷的城市选取数个候选集散点。救援物资首先从供应点运送到选中的集散点，此时由于物资转运量大，需运输时间长，选用直升机直接运输，保证时效性。从选中的集散点运送到各个需求点，此需考虑灵活性，便捷性，选用车辆直接运输。假设如下：

1)供应点、候选集散点和需求点的地理位置关系已知，道路情况可根据现有手段提前获知。

2)救援车辆是同质的，救援车辆始终于同一集散点；救援车辆从集散点出发后，必须返回该集散点，救援车辆的数量不限。

3)当供应点需求量超过配送车辆的最大载重时，超出配送车辆最大载重的部分参与循环配送，剩余满足车辆最大载重的部分直接配送。

1.2 符号说明

1.3 模型构建

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

γijv∈{0,1},γijf∈{0,1},αdv∈{0,1},xs∈{0,1},yl∈{0,1},zv∈{0,1},zf∈{0,1}

(16)

目标函数式(1)车辆、飞机的运输成本最低、集散点的反应成本以及集散点的建立成本最低；式(2)从应急物资供应点运出的量不超过应急物资总量；式(3)表示直升机运输能力约束；式(4)～式(6)表示直升机能且仅能分配给一个供应点，被选中的供应点必须分配直升机且直升机只能分配给供应点；式(7)汽车运输量总量不超过该集散点的总量；式(8)汽车实际运输量不超过供应点需求量；式(9)表示汽车实际运量不超过汽车最大载重；式(10)表示汽车配送路径的延续性；式(11)每辆汽车的配送路径至少连接一个集散点；式(12)表示当且仅当从集散点l出发的运输车辆v经过需求点i时，该需求点i才能分配给车辆v；式(13)～式(15)表示车辆能且仅能分配给一个集散点，被选中的集散点必须分配车辆且车辆只能分配给集散点;式(16)表示0～1变量。

2 算法描述

2.1 基本人工蜂群算法

基于人工蜂群算法(artificial bee colony，ABC)是2005年由土耳其学者Karaboga提出的一种智能算法。ABC算法模仿了蜜蜂采蜜的过程。ABC算法可以有食物源、雇佣蜂、未被雇佣蜂这3个元素，其中未被雇佣蜂又可以分为侦查蜂和跟随蜂。每个食物源代表问题的一个可行解，而该解的优劣则由该食物源质量的好坏来表示。

ABC算法开始时种群由雇佣蜂和跟随蜂组成，一般可以设定为两者的数量分别占种数量的一半，并且食物源数量和雇佣蜂数量相等并一一对应。每只雇佣蜂负责开采一个食物源，在每次迭代过程中，雇佣蜂先对当前食物源附近的食物源进行评估，再由跟随蜂根据反馈信息，基于概率选择一个食物源，并对评估一个邻近的食物源。食物源枯竭的雇佣蜂转化成侦查蜂，随机开发一个新的食物源并重新转化为雇佣蜂。具体算法步骤如下：

步骤1设置人工蜂群规模以及食物源数量，控制参数limit，最大迭代次数max_iter，计算出每个食物源对应的初始解和对应的适应度值。

步骤2雇佣蜂搜索对各自的食物源的邻域，重新获得一个食物源，若新食物源的适应度函数优于当前食物源的适应度，则新食物源对当前食物源进行替换。而邻域操作接受一个解作为输入，返回该解的一个邻域解。

步骤3跟随蜂在每次迭代中根据式(17)的轮盘赌概率选择一个食物源并搜索得到一个新解。

(17)

步骤4若达到局部最优控制参数Limit，即食物源长期未得到改善，则放弃该食物源，雇佣蜂变成侦查蜂，并随机搜索新的食物源。否则，转至步骤2。

步骤5对食物源进行比较，记录最优的适应度对应的食物源。

步骤6判断是否满足停止准则：若迭代小于最大循环次数max_iter，则转至步骤2；否则，停止搜索。

2.2 改进蜂群算法

人工蜂群算法具有操作简单，控制参数少和鲁棒性较强的优点，可以较好地应用于复杂的车辆路径问题。但相比于遗传算法、差分算法，ABC算法只利用适应度值评估解的质量且每个食物源相对独立，没有种群个体之间的交叉操作，导致没用很好利用解的优劣信息，从而影响收敛速度。其次蜂群算法的开发能力有所不足，局部搜索能力较差。针对2E-LRP问题，利用人工蜂群算法框架，结合遗传算法的交叉变异操作并结合大规模邻域搜索的方法来代替原来构建邻域解的方法，通过对解的破坏重组和局部搜索形成新的解。

2.2.1 编码规则

参考文献[11]采用一种实数编码方式，以第一层路径为例。假设集散点的数量为S，供应点的数量为D，则由长度为(S+D+1)向量来表示从一个供应点出发的路径情况，0表示出发的供应点，两个0之间表示依次经过的集散点，若均为0则表示这个集散点未开启。图1表示有2个供应点和4个集散点，第1条路径为从供应点出发经过集散点2和3回到供应点，以此类推，第2条路径为0-1-0。从集散点到需求点也以类似方法进行编码。

图1 编码方式示意图

2.2.2 大规模邻域搜索算法

大规模邻域操作主要有以下3个过程：破坏过程、修复过程和局部搜索过程。在依次进行3个过程后，邻域解可以在较大范围内得到搜索，从而能够较好地跳出局部最优。

运用破坏操作过程中的随机移除操作，修复过程中的贪婪插入操作和局部搜索中的2-opt以及2-opt*。各个方法具体步骤如下：

1)随机移除操作。该操作从当前解的第2层的路径中随机选择若干个需求点，并将被选择点从当前路径中移除并存入需求点池中。

2)贪婪插入过程。将需求点池中的点按随机顺序逐一取出，依次插入当前解，取令当前解最小的位置，为新的解。

3)2-opt* 操作。该操作对同一集散点的路径展开，选择所属某一集散点的任意两条路径: 随机确定交换节点，将路径1前段与路径2后段相连，路径 2 前段与路径 1 后段相连，形成两条新的路径，如果新路径满足条件，并且新路径形成的目标值优于旧路径，则保留新路径。

4)2-opt操作。该操作为对随机选择某路径的任意两个节点，将两交换节点之间的点按照顺序进行反转生成新路径，计算新路径目标值，若目标值变优，则保留当前操作。

2.2.3 算法流程

算法流程如图2所示。

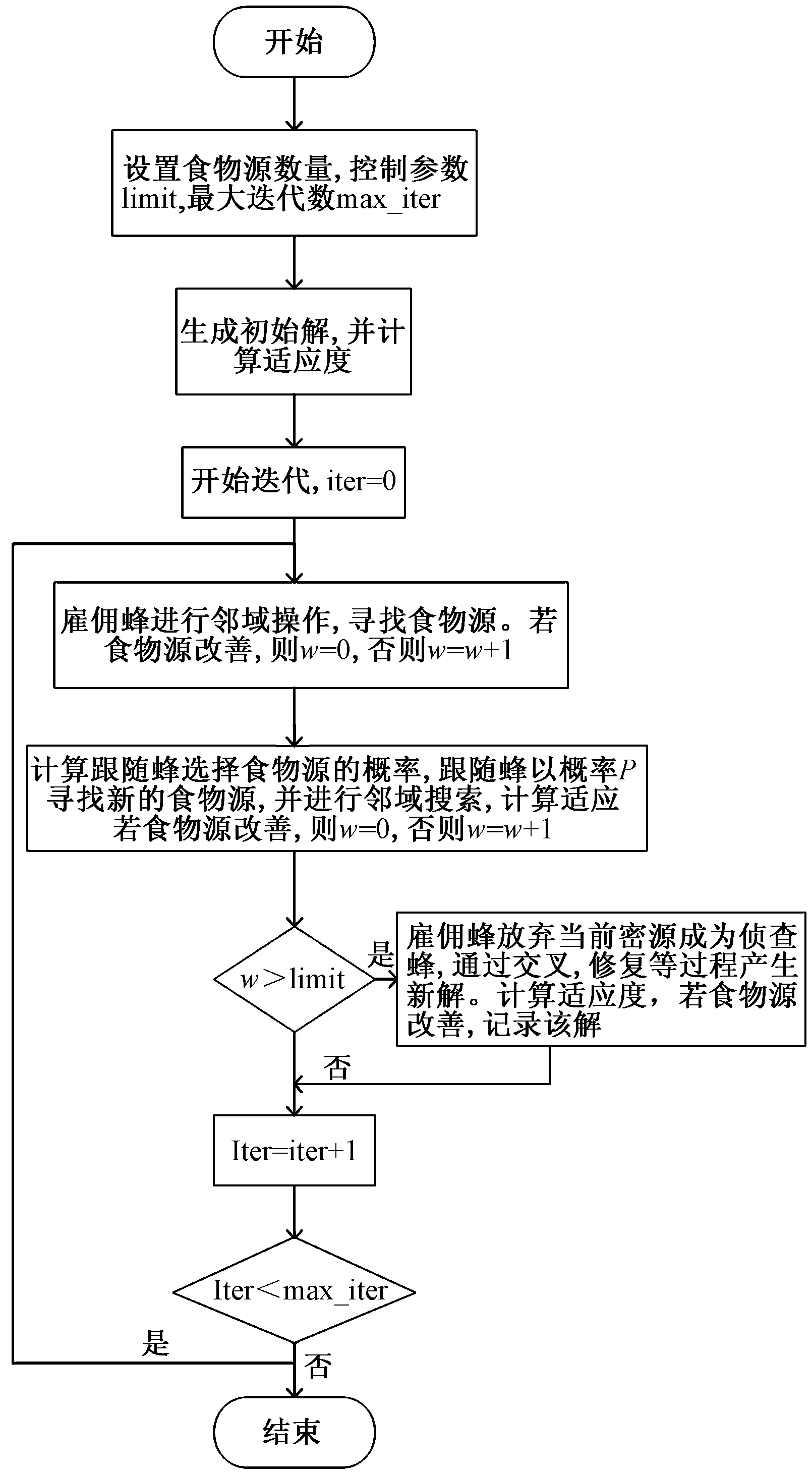
图2 算法流程

3 算例求解

3.1 数据处理

3.1.1 需求点的优先级确定

在现有的大量研究中，对需求点的优先级通过初步判断以及确定的研究较少。程光[12]通过对人口密度、受伤率、老幼比和房屋坍塌比例运用模糊聚类法和熵权法相结合的方式对需求点的优先级进行了划分。通过熵权topsis法相结合，通过需求点的人口密度、地震烈度、死伤率、失踪人数以及老幼比率5个指标对需求点的优先级进行确定，并将逐次逼近距离作为权重，用于衡量需求点的需求量。熵权TOPSIS法是一种将熵权法和TOPSIS法相结合评估优先级的方法。其基本原理首先运用熵权法计算客观权重；在利用TOPSIS法对评估对象进行排序。其具体步骤如下：

1)假设原始矩阵X有m个待评对象，n个评估指标为，则

X=(xij)m×n

(18)

对原始矩阵X通过式(20)、式(21)进行标准化得到标准矩阵R，即

R=(rij)m×n

(19)

式中，rij第i个评估对象在第j个评估指标上的标准值。

对于正向指标(收益型指标)：

(20)

对于逆向指标(损耗型指标)：

(21)

2)标准化的矩阵R第i个被评估对象第j项评估指标下的指标值比重为

(22)

3)计算评估指标第j项的熵值

(23)

4)计算评估指标第j项的权重

(24)

5)得到权重规范后的矩阵

vij=wjrij,i=1,2，…，m;j=1,2，…，n

(25)

6)确定理想解(最优方案)和反理想解(最劣方案)，即

(26)

(27)

式中:J1为收益性指标集，表示在第i个指标上的最优值；J2为损耗性指标集，表示在第i个指标上的最劣值。

q>0,i=1,2,…，m

(28)

q>0,i=1,2,…，m

(29)

8)计算每个评估对象的相对贴近度C*，并根据相对贴近度的大小确定评估对象的优先级，即

(30)

3.1.2 集散点的反应能力

灾难发生后，为更好地向受灾点输送救援物资，集散点发挥重要的作用，不同的集散点对于灾难的反应能力取决于多方面。从地理位置、经济实力、物流发展水平以及基础建设水平出发，通过GDP、货物运输量、公路里程、固定资产等指标[13]，衡量集散点的反应能力。

将指标通过式(20)、式(21)进行标准化，并通过式(31)得到各集散点反应的平均值，即

(31)

以此作为集散点反应能力的差异的度量。

3.2 算例分析

为验证模型和算法的有效性，采用MATLAB(R2017a)编程，首先按照以上部分编程对数据进行处理，再根据算法编写程序。参数设置：食物源及雇佣蜂规模取50，最大迭代数100，控制参数limit取30。在内存为4GB，CPU为Intel2.6GHz的计算机上进行运行。

参考“5.12”汶川大地震的相关灾情信息，选取了2个供应点(昆明S2和重庆S1)、5个候选集散点，14个受灾点。车辆使用的运行成本为1 500元/辆，每公里的运输成本为5元；飞机使用的运输成本为20 000元/辆，每公里的运输成本为500元。集散点和需求点的具体数据如表1、表2所示。按照3.1节的公式对集散点和需求点的数据进行处理，并即处理后的数据应用于算法中。根据以上数据得到物资集散的路径图，如图3所示。

表1 一级配送网络

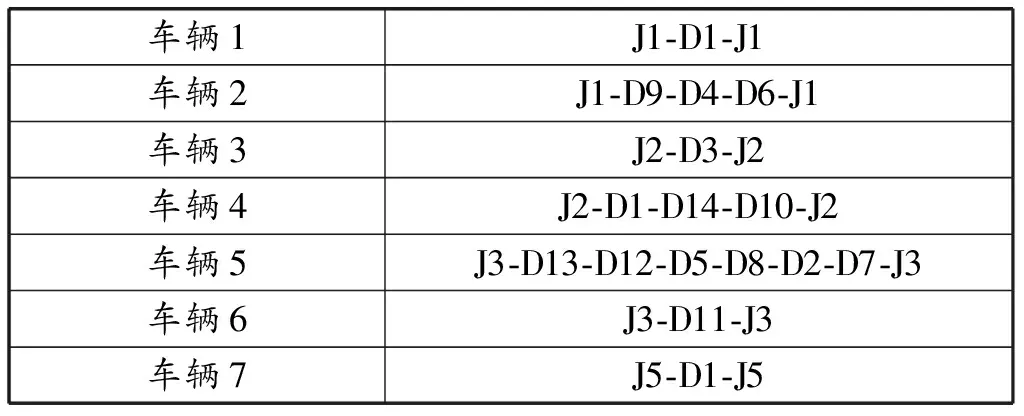
表2 二级配送网络

图3 路径示意图

该物资集散方案共使用7辆汽车和4架飞机，最低成本为2 789 100元，其中需求点汶川县(D1)和北川县(D2)由于受灾严重，需求物资量较大，由循环配送和直运相结合的方式进行运输。具体线路图和车辆使用情况如表3、表4所示。

表3 候选集散点相关数据

表4 需求点基本情况

4 结论

1)综合考虑需求点的优先级和集散点的反应能力，以系统总成本最低构建了一个两阶段定位—路径问题模型，符合实际需求。

2)在考虑需求点的优先级和集散点的反应能力的情况下，可以对候选集散中心进行选择，并根据需求对受灾点进行配送，当单一受灾点物资需求量较大时由多个集散点进行配送，符合实际需求。

3)考虑了单阶段单目标的模型，未来可以进一步研究多阶段需求不确定下的模型。