考虑多轴应力与共振影响的随机振动疲劳寿命预测*
白 金,李 静,仇原鹰,盛 英,孙 红,王海东,王肇喜
(1. 西安电子科技大学 机电工程学院, 陕西 西安 710071; 2. 上海航天精密机械研究所, 上海 201600)
结构在随机载荷的作用下经常处于多轴应力状态,对于在服役过程中承受随机振动激励的航空器或航天器而言,不仅应该关心结构在随机载荷下的多轴应力状态,振动疲劳的问题也必须引起重视。Crandall等[1]将振动疲劳定义为结构在振动作用下产生的不可逆的累积损伤。蒋培等[2]对宽频带随机振动环境下的疲劳强化机理进行了研究。之后姚起杭等[3]指出了振动疲劳中的特殊形式——共振疲劳,即结构因所受动态载荷的频率接近其固频而出现的疲劳破坏现象。王明珠[4]分析了激励频率、阻尼等因素对结构振动疲劳的影响。王锦丽等[5]在研究加载频率对悬臂梁振动疲劳特性的影响中发现:结构在振动过程中,共振会加速裂纹形成或扩展,从而导致结构破坏加剧。
结构在随机振动下疲劳的计算方法主要分为时域法和频域法。时域分析方法是利用时域模拟方法对应力响应功率谱密度函数进行时域模拟,再结合不同的多轴疲劳模型计算。目前国内外学者提出了一些多轴疲劳模型,Socie[6]、Fatemi[7]、Shang[8]等分别基于临界平面法提出了不同的疲劳寿命模型,Li等[9]也基于临界平面法对多轴载荷下的疲劳寿命进行了计算。而在频域法方面,目前大多数的分析方法是利用疲劳失效准则把多轴应力等效为单轴应力状态,再利用应力幅值概率密度函数模型估算结构的疲劳寿命。文献[10-14]提出了不同的雨流幅值概率密度函数模型用于疲劳损伤和寿命估算。无论是时域法还是频域法,均需要结合材料的疲劳寿命曲线进行计算,目前应用最广泛的仍然是单轴拉-压的S-N曲线。但相比于时域分析方法,频域分析方法计算简单、不需要进行循环计数,因此受到了工程界的重视。其中,等效 von- Mises 应力方法[15]是目前工程中常用的多轴疲劳频域分析方法。
此外,以上方法均没有考虑振动过程中共振对疲劳寿命的影响,虽然共振疲劳和一般循环疲劳破坏的机理和临界点基本一致,但实际上二者在结构应力分布、裂纹扩展速率等方面均有很大差异,因此利用这些方法在计算随机振动疲劳时会造成较大误差。也有学者进行了一些材料的共振疲劳试验,肖寿庭等[20]通过对LY12CZ铝合金悬臂梁进行共振疲劳试验,得到了其动态疲劳S-N曲线,但迫于试验成本高、耗费时间多等缺陷,并没有得到很多的试验数据。同时在目前已有的文献中,存在考虑多轴疲劳的,也存在考虑共振对疲劳寿命影响的文献,但可以同时综合考虑两者对疲劳寿命影响的方法目前还尚未见相关文献报道。
所以,提出一种综合考虑多轴应力与共振影响的随机振动疲劳寿命预测方法成为一个有待解决的问题。考虑到新方法不仅应计算方便,更应满足预测精度,因此通过现有的单轴S-N曲线得到随机振动下的多轴S-N曲线,进而利用von-Mises准则预测结构在随机振动下的疲劳寿命成了一个思路。因此,本文通过引入三轴因子FT来反映结构的多轴应力状态,进而为了考虑结构振动过程中共振对结构疲劳寿命的影响,在其基础上定义了多轴振动因子FMV,最终利用单轴拉压和扭转S-N曲线得到了随机振动下的多轴S-N曲线,结合von-Mises准则计算结构的随机振动疲劳寿命,从而得到一种综合考虑多轴应力与共振影响的随机振动疲劳寿命预测方法。
1 基于多轴振动因子插值的多轴S-N曲线
应用von-Mises准则对结构在随机振动下的疲劳寿命进行预测时,应结合可以反映结构多轴应力状态和共振的多轴S-N曲线进行计算。受文献[19]思想的启发,本文提出通过材料的单轴拉-压、扭转S-N曲线线性插值得到对应的多轴S-N曲线,如图1所示。
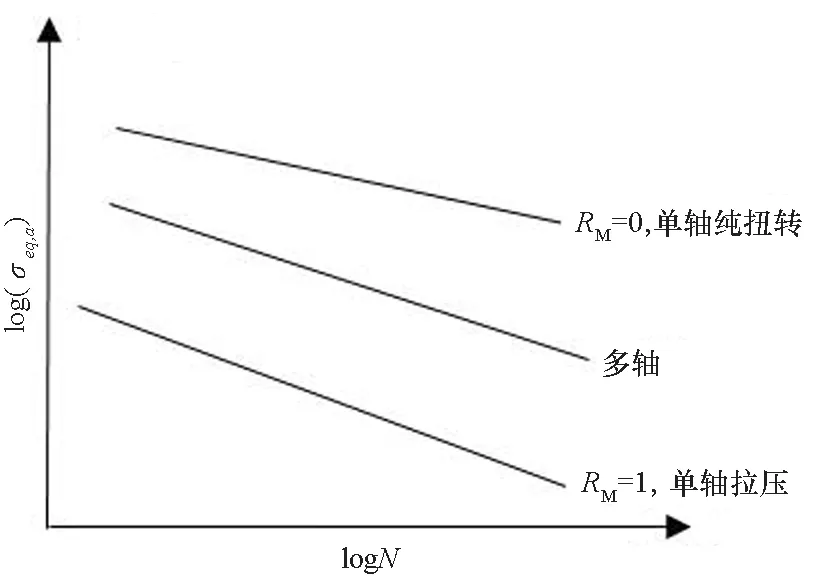
图1 多轴S-N曲线示意图Fig.1 Schematic diagram of multi-axis S-N curve
为了反映结构的多轴应力状态,引入三轴因子[21]FT,其表达式为:
(1)
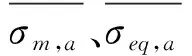
(2)
(3)
但为了便于工程上使用,需要得到FT在频域上的表达式。因此进行如下推导:
(4)
其中:Gσ(f)为应力功率谱密度函数;m0,σ为应力的均方值;Sσm、Sσeq分别为平均应力和等效von-Mises应力的均方根值。
计算结构在随机振动下的疲劳寿命时仅仅考虑其多轴应力状态并不全面,还需要考虑共振的影响。刘文光[22]指出共振疲劳与裂纹联系非常紧密,裂纹在整个振动过程中的开合运动导致结构的动力学特性一直处于变化状态,容易引发一系列非线性共振现象,从而对结构的振动寿命产生影响,从刘文光得到的激励频率对结构疲劳寿命的影响曲线来看,影响曲线的形状与对数函数的形状相似,且考虑到S-N曲线在对数坐标下为直线以及基本初等函数在实际使用中的便利性,因此利用对数函数来表示共振对疲劳寿命的影响。
在振动过程中,结构在共振状态与非共振状态下响应幅值有很大区别,而且共振状态下不同大小的激励引起的响应幅值也不同,对结构疲劳寿命的影响也不同。
综合以上因素,故提出多轴振动因子FMV的表达式如下:
(5)
其中:w是第一阶共振频率处对应的加速度激励功率谱密度值。
多轴振动因子FMV满足以下条件:
1)满足数学表达式的基本要求,即分母不为零,被开方数大于等于零;
2)关于自变量单调递增,即随着第一阶共振频率处对应的加速度激励功率谱密度值的增加,多轴振动因子FMV也增大;
3)在w=1处满足连续条件,在自变量的取值范围内处处连续。
随机振动下的多轴S-N曲线式中的材料常数kmv可以通过FMV线性插值单轴拉-压、扭转S-N曲线的材料常数得到:
kmv=ktor+FMV(kaxi-ktor)
(6)
而随机振动下的多轴S-N曲线式中的材料常数Cmv可以通过FMV在对数坐标下线性插值单轴拉-压、扭转S-N曲线的材料常数得到:
(7)
其中:kmv和Cmv是多轴S-N曲线NSkmv=Cmv的材料常数;kaxi和Caxi,ktor和Ctor分别是单轴拉-压和扭转S-N曲线材料常数。从式(7)不难看出:随着参数FMV的变化,可以得到不同的kmv和Cmv,从而得到不同的多轴S-N曲线。
2 基于随机振动下多轴S-N曲线的疲劳寿命计算方法
利用等效von-Mises应力功率谱密度函数G(f)可直接进行频域寿命计算,其中G(f)的第i阶矩定义如下:
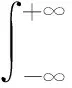
(8)
根据Miner[23]理论,结构的疲劳损伤为:
(9)
式中:ni表示第i级应力水平下的实际应力循环次数;Ni表示应力幅值为Si时S-N曲线下对应的寿命循环值。如果应力状态符合连续分布,则在时间T内,应力处在范围(Si,Si+ΔSi)内的应力循环次数为:
ni=E(P)Tp(Si)ΔSi
(10)
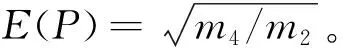
则连续分布的应力状态下时间T内的振动疲劳损伤量为:
(11)
将随机振动下多轴疲劳寿命曲线公式NSkmv=Cmv代入式(11),则连续分布的应力状态下时间T内的振动疲劳损伤量为:
(12)
由Miner线性累积损伤理论,当损伤值等于1时结构发生疲劳破坏,结构的疲劳寿命为:
(13)
对于应力幅值概率密度函数p(S),Tovo-Benasciutti提出的T-B雨流幅值分布模型计算较为准确,因此使用T-B模型进行计算。T-B模型的表达式[11-13]为:
(14)
式中:γ为不规则因子。γ和参数b的表达式分别为:
(15)
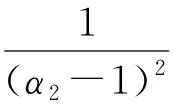
α1α2-α1-α2)exp(2.11α2)+α1-α2]
(16)
式中,α1,α2满足
(17)
3 试验验证
3.1 算例1
7075-T6铝合金材料是一种高强度铝合金,主要用于制造飞机机翼部位的蒙皮和腹板等,而在一些新机试飞时,机翼部位的凸出物和空腔结构会很快发生振动疲劳,因此选用该材料进行验证具有很强的工程意义。文献[24]选用7075-T6铝合金材料的缺口试件进行了随机振动试验,试件厚度为2 mm,预制半径为1 mm的半圆形缺口,试件的几何尺寸、实物图及试件缺口形状详见文献[24],其中材料性能参数如表1所示。

表1 7075-T6铝合金的材料参数Tab.1 Material parameters of 7075-T6 aluminum alloy
利用夹具将缺口试件一端固定在随机振动台上,在另一端通过添加配重改变试件的固有频率和疲劳破坏时间,配重块的数量通过多次预试验确定,配重块的材料为Q235钢。
采用基础激励的加载方式进行试验,激励的方向为样本平面的外法线方向,试验中加载频率范围为14~141 Hz平直谱,如图2所示,不改变带宽,通过改变加速度功率谱密度值改变振动量级。试验过程中通过动态应变仪记录试件固有频率的变化,将固有频率下降10%的时刻作为疲劳破坏的时间点。具体试验细节见文献[24]。
采用有限元计算程序ANSYS软件对试件进行有限元分析,按照试验中的固定方式对试件施加如图2所示的基础随机加速度功率谱激励,同时进行网格划分,网格划分结果如图3所示,共分成7 137个单元和21 434个节点,平均网格质量为0.78。通过对有限元模型进行模态分析得到第一阶固有频率为45.228 Hz,与试验结果46.88 Hz相比相对误差为3.5%,因此保证了有限元分析模型的正确性,同时通过有限元分析可知三轴因子FT=1.38。

图2 基础激励载荷谱Fig.2 Base excitation load spectrum
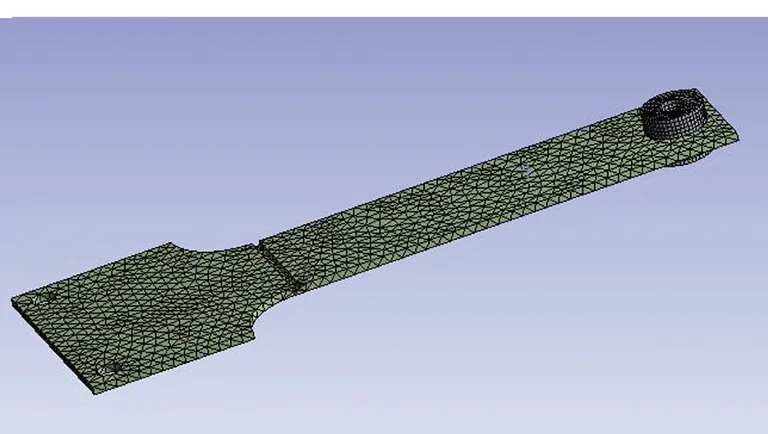
图3 有限元网格划分Fig.3 Finite element mesh generation diagram
根据文献[24]可知:7075-T6铝合金的单轴S-N曲线的材料常数kaxi=9.65,Caxi=6.99×1029;ktor=9.65,Ctor=4.36×1026。根据式(6)、式(7)可得不同随机振动量级下7075-T6的多轴S-N曲线的材料常数如表2所示。
利用有限元分析得到von-Mises的应力功率谱密度函数,同时结合表2中的不同随机振动量级下多轴S-N曲线的材料常数,对该试件在不同随机振动量级下的疲劳寿命进行预测,同时与传统等效von-Mises应力方法(即利用单轴拉-压S-N曲线)和文献[19]中所提的等效Lematire应力方法预测结果以及试验结果进行对比,对比结果如图4所示。通过对多轴S-N曲线和单轴S-N曲线的预测结果进行对比可以看出,两种多轴S-N曲线的预测结果均优于单轴S-N曲线的预测结果。显然,材料在随机振动条件下的多轴应力状态对疲劳寿命有重要影响。
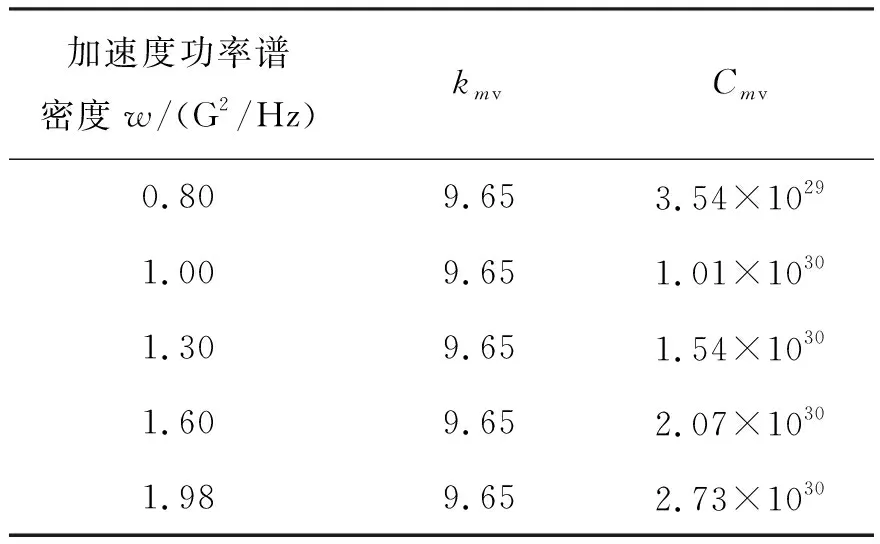
表2 不同随机振动量级下多轴S-N曲线的材料常数Tab.2 Material constants of multi-axis S-N curves with different random vibration orders
同时通过对图4中两种不同的多轴S-N曲线的预测结果进行对比可以看出,由于考虑了共振的影响,因此利用由多轴振动因子插值得到的多轴S-N曲线进行预测的结果最好,而且与不同振动量级下的试验寿命相比,该方法的预测结果均有较高的预测精度。所以预测结构在随机振动下的疲劳寿命时应考虑共振因素。

图4 不同方法下的预测值与试验值比较Fig.4 Predictive and experimental values under different methods
3.2 算例2
以文献[4]中的LY12CZ铝合金U形缺口试件在随机振动下寿命预测为例,对本文方法做进一步验证。试件厚度为2 mm,预制半径为1 mm的U形缺口,试验采用基础振动的加载方式,试验结构为悬臂梁结构,通过夹具将U形缺口试验件固定在激振器上,同时在试件的末端加上配重,配重块的材料为A3钢。试验中加载随机加速度功率谱如图5(a)、图5(b)所示,沿样本平面的外法线方向进行激励并记录疲劳破坏时间。
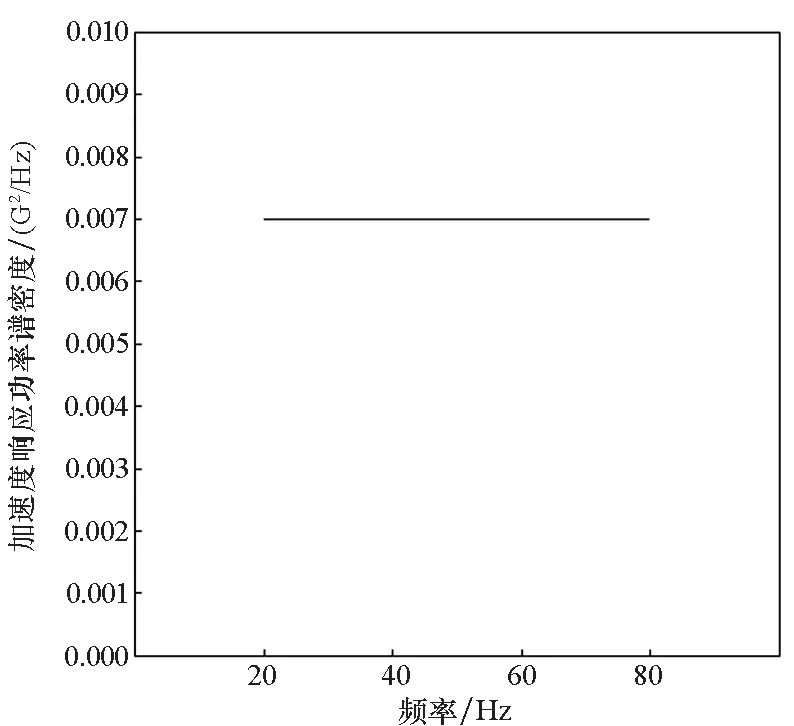
(a) 加速度功率谱密度函数1(a) Acceleration power spectral density function 1

(b) 加速度功率谱密度函数2(b) Acceleration power spectral density function 2图5 基础激励载荷谱Fig.5 Base excitation load spectrum
对试件进行有限元分析,试件有限元模型如图6所示,按照试验中的固定方式对试件固定约束并进行网格划分,共分成45 053个单元和74 632个节点,平均网格质量为0.82。通过对有限元模型进行模态分析得到第一阶固有频率为54.13 Hz,与试验结果54.20 Hz相比相对误差为0.01%;第二阶固有频率为258.52 Hz,与试验结果256.00 Hz相比相对误差为0.98%,因此保证了有限元分析模型的正确性。

图6 有限元模型Fig.6 Finite element model
基于本文提出的方法,采用与算例1类似的计算,可求得LY12CZ铝合金的单轴拉-压和扭转的S-N曲线的表达式分别为lgN=26.3-8.8lgS,lgN=25.1-9.3lgS,多轴S-N曲线的表达式为NS9.3=2×1027。分别利用多轴S-N曲线与单轴拉-压S-N曲线对该试件两种加载工况下的疲劳寿命进行预测,预测结果如表3所示。

表3 两种工况下疲劳寿命预测结果Tab.3 Fatigue life prediction results under two working conditions 单位:min
从表3中不难看出,无论载荷谱是频率范围为20~80 Hz(包含1阶固有频率)还是20~500 Hz(包含2阶固有频率),本文所提多轴S-N曲线的预测结果较单轴S-N曲线更接近试验结果。
4 结论
本文通过综合单轴拉-压、扭转S-N曲线得到了随机振动下的多轴S-N曲线,从而提出了一种新的随机振动疲劳寿命预测方法来预测结构在随机振动作用下的疲劳寿命。新方法的有效性通过预测7075-T6铝合金圆形槽缺口试件和LY12CZ铝合金U形槽缺口试件的疲劳寿命得到了验证,同时可以得到如下结论:
结构在承受随机振动过程中多轴应力状态和共振对结构疲劳损伤的影响不容忽视,因此为了同时考虑这二者对疲劳寿命的影响,提出了多轴振动因子FMV,进而利用该参量综合考虑单轴拉-压和单轴扭转的疲劳S-N曲线,通过线性插值得到了随机振动下的多轴 S-N 曲线。
新提出的随机振动下的多轴S-N曲线不仅可以表征结构多轴应力状态下的疲劳,而且通过引入非线性函数考虑了结构振动过程中共振对疲劳寿命的影响,预测的疲劳寿命的精度明显优于传统的单轴拉压S-N曲线。同时从计算的观点来说,相较于文献[19]中的基于等效Lematire应力的多轴S-N曲线方法,本文提出的方法不仅提高了计算精度,而且更容易计算,便于工程使用。

