概念教学中“发现学习”的实践探索
陆涛
【教学内容】
苏教版五下第三单元“质数和合数”。
【教学目标】
1. 学生通过操作、交流、探索等活动,了解质数和合数的含义,认识百以内的质数表。进一步认识因数和倍数的本质特征。
2. 学生在探索和发现数学知识的过程中,积累数学活动经验,培养观察、比较、分析和归纳的能力,感受一些简单的数学思想,进一步发展数感。
3. 在数学文化的熏陶中,感受数学和生活的联系,培养学习数学的兴趣,增强学习数学的自信心。
【教学重、难点】
1. 了解质数和合数的含义,体会质数和合数的联系。
2. 认识百以内的质数表。
【教学过程】
一、回顾反思,激活经验
1. 回顾发现。
利用课件展示1~20的所有因数。提出问题:仔细观察,说一说你的发现。预设:①一个数最小的因数是1,最大因数是它本身。②1~20里的奇数,除了9和15,因数都只有1和它本身两个。③1~20里的偶数,除2之外,因数个数都有2个以上。
2. 初步分类。
师:根据你发现的因数的个数情况,把这些数分分类,你打算怎么分?
小结:只有1和它本身两个因数的数叫作质数,质数也叫作素数。除了1和它本身,还有其他因数的数叫作合数。
3. 优化判断。
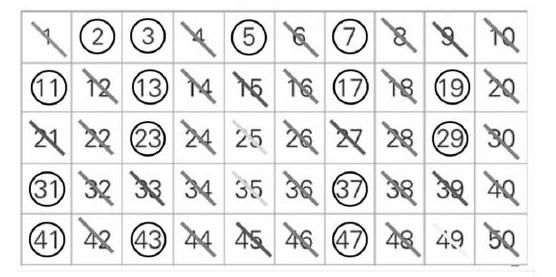
师:通过分类,我们找到了20以内的所有质数,在作业纸的数表中圈出来,一起读一读。(课件展示)
师:刚才我们初步认识了质数和合数,也找出了20以内的质数,下面老师来考考你们。(依次出示18、22、39)这些是质数还是合数?
师:来个大一点的数,47是质数还是合数?
师:怎么快速判断一个自然数是质数还是合数?
小结:在判断质数和合数时,不需要找出所有的因数,只要看能不能找到除1和它本身之外的第3个因数,能找到就是合数,找不到就是质数。
二、自主尝试,发现规律
1. 激发兴趣。
师:接下来找出21~50里的所有质数,比一比,谁先全部找出。
师:你是怎么找的,感觉怎么样?
师:我怎么会比你们快,而且还不遗漏?(学生进行充分猜想)
师:看看我的方法,你发现了什么?
2. 理解本质。
师:是的,老师是把合数去掉,剩下就是质数了,这方法不是我发明的。古代的人们和你们一样,也是一个一个找的,发现很慢,不方便。后来古希腊有位数学家,名字叫埃拉托塞尼,他想了一个办法。首先把1画去,接着找到除2之外的2的倍数,都画去,然后找到除3之外的3的倍数,都画去,再把除5之外的5的倍数画去,最后把除7之外的7的倍数画去,这样剩下的就是质数了。(教师一边讲,一边演示)
师追问:观察上面的方法,你有什么发现?
预设:①1要画去,因为1既不是质数也不是合数。②2、3、5、7都是质数,所以不要画;③4的倍数就是2的倍数,不需要再画;④画完5的倍数还要画7的倍数,别忘了49。
小结:看!这样先画掉1,再画掉除2、3、5、7本身之外的倍数,剩下就是质数的方法,就是埃拉托塞尼的筛选法。
3. 迁移提升。
师:我们把1~50的质数读一读。
师:用筛选法,来找出51~100中的全部质数。
师:首先我们要画掉谁的倍数?接下来呢?
师:下面请同学们自己制作51~100的质数表。
师:你觉得哪个合数容易看成质数?
小结:51和91要特别注意,它们是合数。100以内我们只要先画掉1,然后画掉2、3、5、7的倍数,剩下的就是质数了。100以外的质数我们以后还会进一步学习。
三、整体感知,构建联系
师:同学们自己制作出了这张100以内的质数表(图略),先读一读,再前后桌四个人交流一下,你了解到了什么。
预设:①100以内质数有25个,合数有74个。(追问:怎么只有74个)②2是质数里唯一一个偶數。(追问:还有其他偶数是质数吗)③1既不是质数也不是合数,但它是一个奇数。④2是最小的质数。4是最小的合数。⑤奇数也可能是合数,也可能是质数。(追问:奇数都是质数吗)
小结:今天学习的质数与合数和之前的奇数与偶数之间也存在着密切的联系。
四、生活应用,提升素养
1. 猜一猜。
师:玩个游戏,下面是老师的QQ号,你能根据提示猜一猜吗?
出示:3 6 □ 1 8 □ 3 2 □ ,①第3位是质数也是偶数。②第6位比最小的合数多1。③第9位在10以内,既是奇数,又是合数。
过渡:通过游戏我们进一步发现了质数和合数与奇数和偶数间的联系,其实它们之间还藏着更深刻的秘密等待着你的发现呢!
2. 分一分。
把下面的糖果分给两个小朋友,而且每个小朋友拿到的糖果数都是质数。8=(?摇?摇?摇?摇)+(?摇?摇?摇?摇),12=(?摇?摇?摇?摇)+(?摇?摇?摇?摇),15=(?摇?摇?摇?摇)+(?摇?摇?摇?摇),18=(?摇?摇?摇?摇)+(?摇?摇?摇?摇)=(?摇?摇?摇?摇)+(?摇?摇?摇?摇)。
师:看看等式的左边和右边,你有什么发现?
预设:①等式左边都是合数,右边是质数。②任何一个合数都可以拆成两个质数之和。③左边有偶数也有奇数。
师:你们的发现和数学中著名的“哥德巴赫猜想”就很接近了。[出示:任何大于2的偶数都是两个素数(质数)之和]
师追问:为什么这里强调任何大于2的偶数?(强调2是唯一一个偶质数)
小结:通过分一分,我们发现并初步感受了伟大的数学猜想,为自己鼓掌!
3. 赏一赏。
师:同学们,质数的研究永无止境,它就像一个数概念中的万花筒,在我们的生活中处处可以欣赏到它的美。
依次出示:回文质数、正倒质数、去尾质数、孪生质数等。
(作者单位:江苏省无锡师范附属小学?摇?摇?摇?摇责任编辑:王彬)

