以史为鉴积累数学活动经验
郭耀宇
历史是教学的指南,数学史能够呈现数学知识的来龙去脉。数学学科知识中有不少来源于人们在现实生活中的观察与实践总结。数学教师如果能够结合数学史料,精心设计一些探究活动或实验操作,那么学生便能亲身经历数学知识的发生发展过程,做到知其然并知其所以然。本文试以圆面积计算公式的推导为例,以圆面积计算在数学史上的发生发展来设计相关活动,从借鉴数学史教学价值的角度来谈谈如何积累数学活动经验,提高学生的数学素养。
一、重现数学史,通过实验操作积累数学活动经验
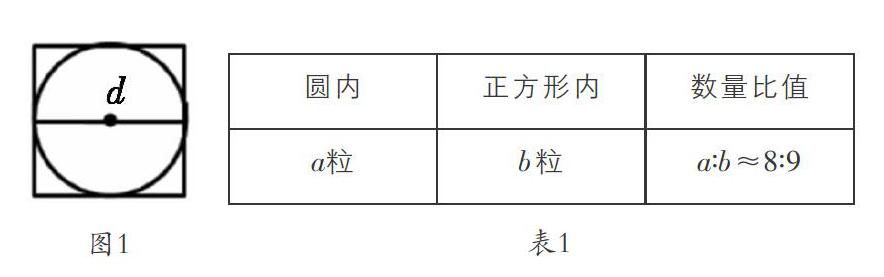
古埃及莱茵德草书第50题这样记录:假设一直径为9的圆形土地,其面积等于边长为8的正方形面积。这说明古埃及人有了圆面积的近似计算公式。基于这一史实,笔者先请学生回忆以前长方形面积公式的推导过程,明确了是用单位正方形先去数个数,然后再推导公式。接着在课堂上安排了两个实验,实验一:以观察为主,课件展示用单位正方形来铺满圆,发现总有缝隙或超出,无法契合铺满,引出用直边图形面积直接代替曲边图形面积的矛盾冲突。实验二:以操作为主,告知学生古埃及圆的面积计算公式相传是从数谷粒的方法中归纳得到的,让学生通过实验操作来经历这个过程。给每个学习小组(四人一组,共十组)分发一个“外方内圆”的图形(图1),每个小组圆的直径大小不等。实验步骤1:挑一挑——学习小组从组长带来的米粒中挑选出大小均匀的米粒(讨论并明确为什么要大小均匀)。步骤2:铺一铺——把大小均匀的米粒铺满整个圆并记录下米粒数,然后把四个边角的空白也铺满,即铺满与其外切的正方形,并记录下米粒数。步骤3:说一说——讨论铺的过程为什么要尽量做到不重叠又不留缝隙(这样才能尽最大可能逼近图形的近似面积)。步骤4:算一算——计算铺满圆与铺满正方形的米粒数量之间的比值(表1)。步骤5:辨一辨——明确这个比值就是这两个图形面积间的关系,用正方形的面积乘这个比值就等于圆的面积。步骤6:想一想——此时因为有了各组实验数据的支撑,而学生又知道正方形的面积是可以用公式计算的,所以完全可以抛开正方形内的米粒数而用正方形的面积乘这个比值,圆的面积就可以被粗略地计算出来了,即圆的面积大约等于正方形面积的。
这个实验操作虽然无法精确地得到圆的面积计算公式,但学生通过“挑—铺—说—算—辨—想”等实验操作积累了一定的数学活动经验,知道了圆面积计算最早发生的形态。这会激起学生的学习兴趣,更重要的是在积累活动经验的过程中感知到曲边图形(圆)与直边图形(正方形)的面积有一定的关联,这使得后续将圆转化为长方形来求得面积变得更为顺理成章。
二、借鉴数学史,通过合作探究积累数学活动经验
学生在上述实验操作中萌发了把圆面积转化成直边图形面积来研究的想法,于是笔者启发学生回顾平行四边形的面积是如何通过割补法转化成长方形面积的过程。在转化思想的支撑下,进行了如下对话。
师:“大家能应用转化的方法合作探究出圆的面积吗?”生1:“可以把圆切开,重新拼接。”师:“任意切可以吗?”生2:“可以在圆里面切出一个正方形或长方形。”师:“切完四边形后,外围剩下的4小块还是曲边图形,没法计算。”生3:“可以沿着半径切。”生4:“可以沿着直径切。”……此时,笔者再顺水推舟介绍数学史上古印度数学家关于圆面积的探究:古印度数学家受切西瓜的启发,把圆切成小瓣,然后把这些小瓣上下对接(介绍到此为止,不再往下)。接下来在切西瓜这一动作表象的作用下,请学生用带来的圆形纸片在小组内合作学习,探究圆面积该如何计算。为了使探究活动更为高效,笔者建议学习小组对圆进行偶数等分。各个学习小组分别对圆进行了四等分、六等分、八等分、十等分、十二等分、十六等分,然后重新拼接。随着等分的份数逐渐增加,笔者使用希沃授课助手将各小组拼摆的图形投影到屏幕上进行对比,学生强烈地感受到分的份数越多,拼接出来的图形越接近于长方形,这样就可以把圆的面积转化成长方形的面积来计算。此时笔者再追问:“圆的面积大小有变化吗?”生:“不变,圆的面积转化成长方形的面积。”师:“长方形的面积=长×宽,那么这个长方形的长和宽分别是哪条?等于什么?”因为有亲身的探究经历,学生轻松答出长方形的长等于圆周长的一半,即πr,宽等于半径,即r,于是得到了圆的面积计算公式:S=πr2。在整个公式的推导过程中,学生密切合作,他们完成了等分、拼接、交流、推导四个探究活动。通过这些探究活动,学生经历了圆面积转化及其计算公式产生、发展、形成的过程,既感受了数学逻辑推理的严谨性,又发展了思维能力。这不仅帮助学生积累活动经验,而且极大地提升了学生的数学素养。
三、联系数学史,通过学以致用积累数学活动经验
学习金字塔告诉我们:输出式学习是一种最高效的学习方式。学以致用则是输出式学习的直接表现。让学生在学会圆的面积计算之后,立刻加以应用,不但能巩固所学,而且在应用中能体会到数学与生活的联系。
笔者在课堂上设计了一道马儿吃草的问题:马的缰绳被绑在一个树桩上,已知绳子的长度是5米,求这匹马能吃到草的最大面积是多少?在解决这个问题的过程中,能帮助学生体验从生活经验向数学活动经验的升华,这样的升华能帮助学生从现实生活或者具体情境中抽象出数学问题并选择适当的策略加以解决。接下来,学生展示了这道题的两种解决策略:一是直接应用公式S=πr2进行解答;二是应用S=πr×r进行计算。从学生的发言中得知,在解题的过程中他们想到了圆的面积就是转化后的长方形面积,长方形的长是圆周长的一半,宽是圆的半径,当想到了长×宽就想到了πr×r。第二种解决策略说明了学生对探究活动的过程和结果已完成了内化,凸显了利用数学活动获得知识、形成能力的独特价值。此时可联系数学史,借助多媒体展示“圆田术”:大约在1800多年前,汉代数学家刘徽对《九章算术》中记载的圆面积公式(圆田术)进行注解——半周半径相乘,得积步。也就是说圓面积等于圆的一半周长乘半径,这样联系数学史的学以致用,让学生的数学活动经验得以积累,学习的热情得以激发。
总之,数学史犹如一座神奇的数学宝藏,它蕴含着丰富的知识、方法和思想,只要我们深入挖掘,精心设计,必能为学生提供实验操作、合作探究、学以致用机会,让学生经历数学知识发生发展的全过程,从而积累丰富的数学活动经验。

