深度说理，促进数学核心素养的形成

柳榕

数学是自然科学的重要基础，是学校教育必不可少的基础学科。由于有些教师对教学不求甚解，把原来最讲道理的数学搞成了“不讲理的学问”，使学生对数学产生了恐惧感。那么该如何体现数学知识的美感和价值呢？笔者认为，可以通过数学课堂培养学生深度说理，促进数学核心素养的形成，让学生发现数学美，欣赏数学美，体会学数学的真正意义。

一、注重算理，学会表达

我们处在一个网络时代，一年级的新生从小就接触电子产品，再加上学前教育的普及，新生入学前就对于一年级数学知识或多或少有些了解。一年级的新生想说也爱说，所以应该多给他们表达的机会。课堂教学时间毕竟有限，不可能让每个学生畅所欲言，教师可以利用钉钉等网络平台，挑选一些重难点例题，让学生通过拍视频的方式说说解题方法和理由，突破课堂时间不足的问题。

如在教学“两位数减一位数（退位减）”时，笔者欣喜地发现学生对“36-8”这一列式表达出精彩纷呈的算法：①先算36-6=30，再算30-2=28;②把36分成20和16，先算16-8=8，再算20+8=28;③把36分成16和20，先算20-8=12，再算16+12=28;④把36分成6和30，先算30-8=22，再算6+22=28;⑤把36分成26和10，先算10-8=2，再算26+2=28;⑥先算8-6=2，再算30-2=28。其中算法①和算法②是教科书上呈现的，算法③、④、⑤和算法②相类似，都是用数的组成和整十数的退位减法计算得出，只是不同学生的思维习惯不同，出现被减数不同的组成，引发不同的计算方法。倒是算法⑥颇让人意外，被减数36的个位6不够減，与减数8比差了2，所以30要再减2等于28。算法①和算法⑥殊途同归，最后都是算30-2=28，算法①其实省略了把减数8分成6和2的步骤，然后被减数36连续减去6和2，两相比较算法⑥更为简洁，所以部分思维比较活跃的学生很快接受了算法⑥。学生在多样化的算法中整理并交流计算方法，真正理解算理，掌握计算方法。

二、结合实践，厘清数理

数学语言是抽象概括的，之所以给人以晦涩难懂的感觉，是因为脱离了生活实践。陶行知先生说：“事怎样做就怎样学，怎样学就怎样教;教的法子要根据学的法子，学的法子要根据做的法子。”

如在教学“多得多和少得多，多一些和少一些”的区别时，笔者发现学生的数感和表达能力有所欠缺，无法正确描述数之间的大小关系。这时候，笔者引入米尺这一工具，让学生在米尺上找到笔者提出的数字，直观比较它们之间的距离。从而使学生逐步感知不同数字间的大小，再判断数字之间相比的差是“多一些”还是“多得多”，是“少一些”还是“少得多”。米尺这个直观形象的数学教具，还可以应用在“小数的意义”教学上，如笔者提问：把1米平均分成100份，每份长多少，结合米尺说说0.01米表示的意义，能否在米尺上分别找出0.17米和0.60米？这些问题从学生的生活经验而来，从实际背景中抽象出数学问题、构建数学模型、寻求结果、解决问题，使学生感受到数学来源于生活，又应用于生活。

三、潜移默化，渗透思想

子曰：“学而不思则罔，思而不学则殆。”康德也说：“感性无知性则盲，知性无感性则空。”数学思想方法是数学的精髓，在教学过程中渗透数学思想方法能显著提高学生的数学核心素养。数学知识的学习过程就是数学思想方法的养成过程，比如说数形结合思想，一年级起就可以引导学生画示意图表示数。

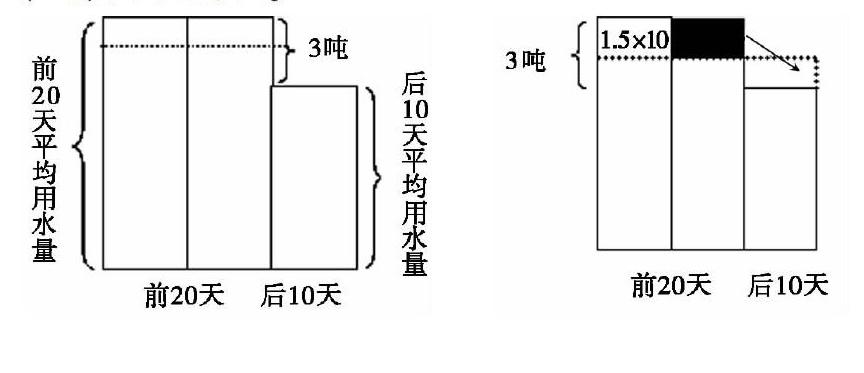
如人教版一年级上册第79页的例6：小丽排第10，小宇排第15，小丽和小宇之间有几人？这类题目用画圆圈的方式表示出第10到第15的数，就能迅速找出答案了。之后的教学可继续引进线段图、矩形图、树状图和韦恩图等来解决问题。再如，在高年级出现的一道题：随着节约用水活动的深入开展，学校4月份后10天平均用水量比前20天平均用水量低3吨。小东把前20天平均用水量加上后10天平均用水量再除以2，这样得到的结果与4月份学校真正的日平均用水量相差多少吨？这道题可引导学生根据题意画出长方形图，用长、宽分别表示日平均用水量和天数，则面积表示用水总量。前20天多的用水量是“3×20”吨，平均分成两份，每份是“1.5×20”吨。“1.5×20”吨再平均分成两份，每份是“1.5×10”吨，其中的一份通过“移多补少”给后10天，最后多的一份“1.5×10”吨平均分给30天，得到的0.5吨就是小东的计算结果与4月份学校真正的日平均用水量的差。

四、深度说理，提升素养

让学习真正发生，教师对教材及知识体系应有整体的理解，对学生学情有深入的了解，对课堂对话交流有娴熟的把控，才能做到统筹有度、有的放矢，拨动提问之弦，撬动思考之源，学生才有可能真正成为课堂的主人，才能真探究说真理。课堂的探究如何发生呢？问题的引发是关键，教师设计的核心问题决定了课堂的走向及探究的深度。

例如，学生对能被2、3、5整除的数的特征都能熟记并加以应用，但是却不知道判断2、3、5倍数特征的道理。罗鸣亮老师就针对此内容上了一节精彩绝伦的公开课“你知道吗？”。罗老师先在十位上写出数字1（10是5的倍数），接着在计数器的十位上拨珠子，学生发现不管几个十都是5的倍数。罗老师随后在计数器的百位上拨珠子，一百里面有10个十，是5的倍数，几个百就是几十个十，都是5的倍数。以此类推，学生发现千位上的数是几百个十，万位上的数是几千个十……都是5的倍数。罗老师继续抛出问题：“在个位上随意拨珠子，还是5的倍数吗？”让学生准确把握为什么判断5的倍数只要看个位而不用看其他数位的道理，进而类比迁移理解2的倍数特征。学生兴趣盎然，根据罗老师提供的探究单继续研究3的倍数特征之“理”。探究单上有一个数字12，学生在罗老师的指引下发现十位上的1可以分成10个一，10除以3余1，这个1和个位上的2相加等于3，这个3可以被3整除，所以12是3的倍数。而对于142里的1个百，3个3个地分余1个1，4个十分别3个3个地分余4个1，把余下来的1、4和个位上的2相加等于7，7不能被3整除，所以142不是3的倍数。课后学生收获满满：“以前数学课只看一个数各位上的数的和是否是3的倍数，没明白为什么这样，今天彻底明白了。”罗老师教学的这一课，与其说是探索知识背后的秘密，不如说是数学精神的洗礼和文化的熏陶。

总之，深度学习对教师的专业成长提出了更高的要求，教是为了“不教”，教师“不说”是为了学生更充分地说。教师要搭建适合学生探究学习的平台，适时点拨，给学生思考的空间与时间，他们才能在知识关联处深入思考，才能说得开理得顺，并能探寻知识背后的原因，培养学习能力以形成素养。开放问题帮助学生打开五彩斑斓的数学世界，让知识学习有深度，学生也在知理、明理、说理中品尝学习之甘甜，构建“讲道理”的数学课堂，生本课堂也就自然落地生根。

（作者单位：福建省福州市长乐区泮野中心小学）