基于单摆方程的电力系统同调性量化分析

刘学华，魏繁荣

(1.国电南京自动化股份有限公司,江苏 南京 211106；2.美国罗德岛大学电气计算机及生物医学工程系，美国 罗德岛州 金士顿 02881)

0 引言

大规模电力系统的动态安全分析需考虑预想故障、运方调整以及特高压与新能源接入等因素的影响[1—3]。为了快速校核电网的安全稳定性[4—5]，工程上一般根据电力系统微分方程或受扰轨迹，基于故障场景将复杂高维的实际系统等值为简单低阶的小系统[6]，该过程称为电力系统的动态等值。

动态等值一般基于发电机转子角或母线电压的同调特性[7]，即受扰动后对应状态量或代数量响应运动趋势的一致性[8]。研究中常使用2台发电机的相对转子角偏差衡量其同调程度[9]。电力系统受扰后发电机响应的非同调可能导致动态等值不准确，使等值系统的静态或暂态稳定分析结果无法反映系统的真实动态特性，影响系统的安全稳定分析[10]。

当前电力系统同调性研究按对象不同分为三类：模型法、轨迹法以及混合法。模型法基于电力系统拓扑及发电机模型参数预测其时域响应的同调特性。传统模型法多采用频域近似或特征模式分析[11—12]，根据关键特征向量的相位辨识发电机同调分群[13]。但实际系统的动态特性与线性模型不完全相同，因此有研究尝试直接根据系统参数计算机电距离，进而评估同调性[14—15]。轨迹法直接从受扰轨迹提取同调信息或信号特征，对发电机进行聚类[16]。一类研究应用人工智能直接构建发电机转子角轨迹特征到系统同调性的映射关系，代表方法有支持向量机与人工神经网络[17—18]；另一类研究尝试从轨迹中提取信号特征，典型方法有奇异值分解与谱聚类[19—20]。

模型法难以处理系统动态特性随扰动场景变化的问题，轨迹法缺乏机理分析，导致强壮性不足[21]。为此，有研究结合模型与轨迹分析暂态能量函数与电力系统同调性的关联关系，即混合法[22—23]。文献[24]研究了发电机同调与动态等值的关系，提出原系统理想同调与等值系统保留全部动态特性的等价性。然而，任何现有方法都无法辨识理想同调的发电机分群。因此，有必要研究电力系统同调性的量化分析方法，评估电力系统动态等值的准确性，为电力系统安全稳定分析提供支撑。文中基于单摆方程分析了电力系统受扰后的动态特性，提出理想同调情况下动态等值系统运动周期的估算方法，从估算周期与实测周期的差值中提取指，标实现电力系统同调性的量化分析，为电力系统安全稳定校核提供参考。

1 电力系统的动态等值

按照不同的参考基准，基于发电机受扰轨迹的动态等值方法可分为角度中心(center of angle，COA)等值与惯量中心(center of inertial，COI)等值。前者将所有发电机角度的代数平均值作为COA，常用于研究单台发电机相对COA的运动特性；后者按照各机惯量大小对发电机转子角进行加权得到COI，典型应用是电力系统暂态稳定的扩展等面积准则(extended equal area criterion，EEAC)[25]。

从数学模型角度研究等值系统的动态特性，文中选择具有明确物理意义的COI等值。具有n台发电机的原系统经一系列变换，受扰后的响应特性被描述为单机无穷大系统(single machine infinite bus，SMIB)。不计阻尼时，等值系统动态模型可表示为微分方程：

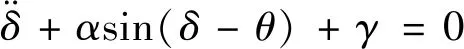
(1)

式中：δ为惯量等值系统的发电机角度；α，θ分别为等值系统功率特性正弦分量的幅值与相位；γ为等值系统微分方程的常数项。各参数的详细定义可参考EEAC理论。

2 单摆方程的周期特性

2.1 典型等值受扰轨迹

电力系统受扰后的动态过程一般包含等值SMIB角度的多个往复运动摆次，如图1所示。将等值SMIB角度的局部极大值称为上边界(upper boundary point，UBP)，对应地将其局部极小值称为下边界(lower boundary point，LBP)。

图 1 等值SMIB的角度曲线Fig.1 Angle curve of equivalent SMIB

图1中，δUBP，δLBP分别为UBP和LBP对应的功角；tUBP，tLBP分别为UBP和LBP对应的时间；Ta为实际等值轨迹的运动周期。

因实际振荡中UBP与LBP的时序关系并不确定，为方便推导，参考图1中UBP和LBP相对位置，假设δLBP<δUBP，tLBP>tUBP，且Ta=2(tLBP-tUBP)。

2.2 动态等值系统的单摆方程

式(1)为等值SMIB的微分方程。令等值角速度ω为：

ωBω=dδ/dt

(2)

式中：ωB为ω的标幺基值，取314 rad/s。则：

(3)

将式(3)代入式(1)得：

ωBωdω=-γdδ-αsin(δ-θ)dδ

(4)

以UBP为起点，针对δ从δUBP运动到δLBP过程中任一点，式(4)两边求积分得：

(5)

式中：ωUBP为UBP对应的角速度。

式(5)中积分展开为：

(6)

考虑到边界点处ωUBP=ωLBP=0，将式(6)变形可得UBP与LBP之间任意ω为：

ω={2|-γ(δ-δUBP)+α[cos(δ-θ)-
cos(δUBP-θ)]|/ωB}1/2

(7)

类似于理想的单摆模型，任意位置的速度仅与位移有关，与时间无关。取任意时刻等值发电机转子角到积分起始点的N等分：

Δδ=(δ-δUBP)/N

(8)

则第k个点等值发电机角度为：

δk=δUBP+kΔδ

(9)

为研究等值系统的动态特性，设第k段Δδ微元对应时间的微增量为：

Δtk=Δδ/ωk

(10)

式中：ωk为第k个点的角速度。

则系统从起始点UBP运行到任意位置所用的时间tΣ可表示为所有分段时间微增量的累加。

(11)

当分析点取为LBP时，tΣ反映了等值角度的轨迹从UBP到LBP所用的时间，即tLBP-tUBP，具有半周期的物理意义。令N→，则式(11)可改写为连续积分形式，定义其为无阻尼估算周期TO。

(12)

2.3 阻尼力矩的近似校正量

将式(5)中积分上限设为ωLBP，δLBP，研究等值系统从UBP运行到LBP的过程。

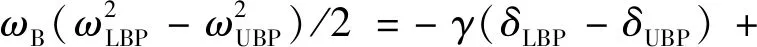
(13)

式(13)等号左边描述了等值系统在UBP和LBP处动能的变化量，考虑到边界点处ω为0，式(13)等号右边恒等于0，定义δ从δUBP运行到δLBP的过程中阻尼做功WD为：

WD=γ(δLBP-δUBP)-
α[cos(δLBP-θ)+cos(δUBP-θ)]

(14)

实际系统中，阻尼力矩叠加在加/减速力矩中影响任意点的角加速度，从而对等值SMIB做功，任一点的阻尼力矩大小与角速度直接相关，无法通过式(1)的微分方程求解。为了在等值SMIB动态特性分析中计及阻尼力矩影响，假设阻尼转矩在角度位移过程中平均做功。令：

WD=wD(δ-δUBP)

(15)

相当于将WD从数值上分解为N等份，平均分配到UBP到LBP之间N个Δδ分段中，则：

wD=WD/(δLBP-δUBP)

(16)

由此，等值SMIB的微分方程在δ从δUBP运动到δLBP的过程中被修正为：

(17)

则估算计及阻尼力矩后等值SMIB的周期TD为：

(18)

理论上式(12)和式(18)均可变换为非完全的椭圆积分形式，从而化简为初等积分。然而，实际工程计算中，根据积分轨迹或实测轨迹得到UBP与LBP的坐标后，易使用数值方法求取TO，WD，TD。

3 等值系统同调性的量化评估指标

当系统理想同调且阻尼为0时，其动态模型可等值为参数定常的SMIB，如式(1)所示。此时，无阻尼估算周期与实测周期相等，即TO=Ta。若系统阻尼力矩不为0，则式(17)可近似描述等值SMIB的动态特性，有TD≈Ta。换言之，一般地，电力系统理想同调时可以用TD近似描述其动态响应的周期特性；特殊地，阻尼为0时，TD=TO≈Ta的数值解。

定义动态等值的SMIB周期估算误差为：

(19)

ε评估了理想同调假设下，估算周期与实际轨迹测量周期的差异，量化反映了原系统受扰轨迹的非同调特性。因此，设计基于单摆方程的电力系统同调性评估指标为：

I=min(1,|1-ε|)×100%

(20)

I量化评估了确定分群模式后，等值SMIB角度轨迹的同调程度，I∈(0,100%]。当I为100%时，SMIB理想同调，估算周期无误差；随着I减小，系统同调性不断降低。算例分析显示，I的取值与动态等值的主导分群模式有关。当动态等值的分群模式与实际振荡一致时，I数值较大(一般大于70%)；当多个分群模式同时作用时，I的数值一般为50%～70%；当所选分群模式非主导时，I的数值一般低于50%。

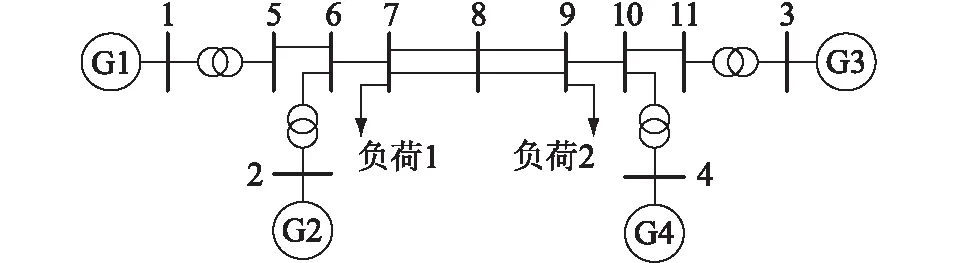
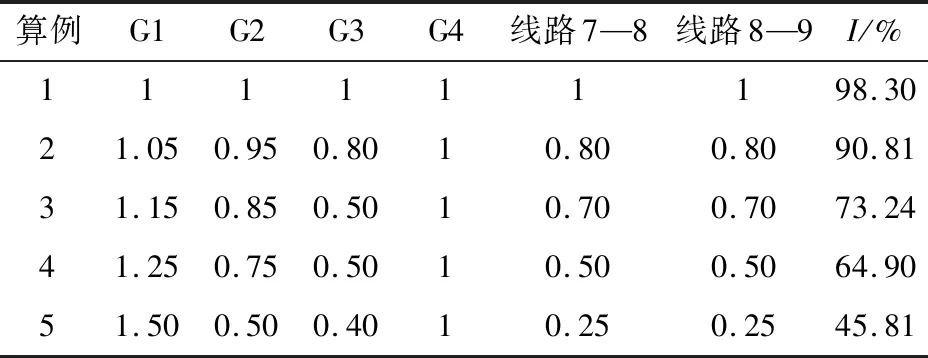
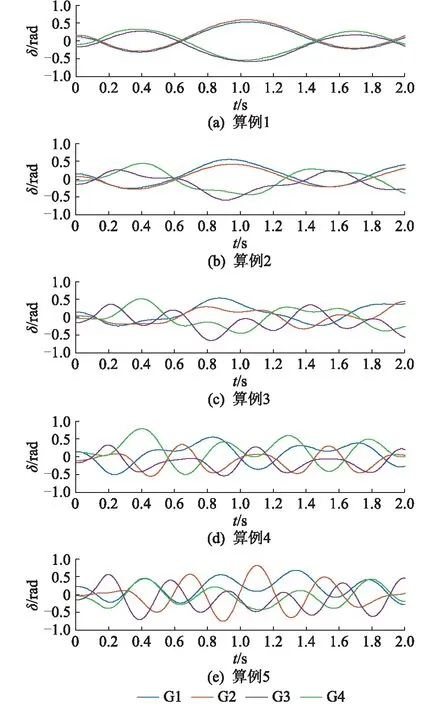
另外，结合仿真可知，阻尼力矩起积极作用时，其可抑制等值SMIB角度曲线的发散。wD作用使角速度小于0阻尼力矩时的情况，有TD>TO；反之，若阻尼力矩起负面作用，有TD

D=(TD-TO)/TO

(21)

由此，基于2个估算周期的差值可以实现等值系统阻尼力矩作用效果的定量评估。

4 算例分析

4.1 SMIB同调性分析

基于SMIB验证文中所提周期估算方法以及阻尼特性评估指标的准确性，系统拓扑如图 2所示。发电机采用经典二阶模型，负荷假定为恒阻抗。

图2 SMIB拓扑Fig.2 Topology of SMIB

SMIB为理想同调多机系统的动态等值，经典模型中阻尼力矩仅与发电机阻尼转矩系数有关，该系统适用于校核TD的准确性以及指标D与系统阻尼特性的关联关系。系统在临界稳定状态时，电磁功率特性在UBP和LBP附近具有很强的非线性，具体表现为边界点处角加速度接近0，周期估算误差较大。故障清除时间对时域响应周期特性的影响如图 3所示。0时刻在节点2设置三相瞬时短路故障，故障持续时间分别为0.02 s，0.070 4 s，其中0.070 4 s为临界故障清除时间。

图3 故障清除时间对时域响应周期特性的影响Fig.3 The influence of fault clearing time on time domain response period characteristics

由图3可知，临界稳定时清除故障，波形振荡周期增大。因此，使用瞬时故障与临界故障分别校核TD，D在一般情况与极端情况的准确性。仿真中，瞬时故障设置为线路2—3首端发生三相瞬时短路，故障在0.02 s时自动消失，改变发电机阻尼转矩系数，测量Ta，计算TO，TD，ε，D，如表 1所示。

表1 不同阻尼系数的SMIB瞬时故障后周期与阻尼估算Table 1 The period and damping estimation of SMIB after transient fault under different damping coefficients

表1中，根据式(19)可估算SMIB的TD相对Ta的误差平均值为0.25%，且误差均小于1%，验证了文中方法通过UBP和LBP的信息可准确推算转子角运动的半周期。另外，作为该系统唯一的阻尼力矩来源，发电机阻尼转矩系数与系统阻尼成正比，文中所提定量指标D的符号与发电机阻尼转矩系数始终保持一致，且其数值与阻尼转矩系数具有单调关系，一定程度上展示了SMIB动态过程的阻尼特性。

临界故障类型的地点信息与瞬时故障相同，短路自动消失时间调整为首摆不发生暂态失稳的临界清除时间，此时电力系统首摆与次摆的动态过程具有极强的非线性，相较普通故障，其周期特性发生畸变，如图 3所示。针对临界故障后首个UBP和LBP，分别计算TO，TD，ε，D，如表 2所示。大量算例证实，该类情况一般代表了相应故障场景周期估算的最大误差。

表2 不同阻尼系数的SMIB临界故障后周期与阻尼估算Table 2 The period and damping estimation of SMIB after critical fault under different damping coefficients

由表2可知，在极端的临界故障情况下，TD相对Ta的误差平均值为2.11%，依然保持在较低水平。指标D与系统阻尼力矩的关系依然保持正相关。另外，阻尼为负时，TD与TO的偏差变大；阻尼为正时，TD与TO的偏差变小。负阻尼的临界算例中第二摆发生暂态失稳，周期畸变的原因包含扰动注入能量与负阻尼力矩两方面。正阻尼的临界算例中后续摆次是稳定的，周期畸变的原因主要为扰动注入的能量。

4.2 4机11节点系统同调性分析

为了验证文中指标分析系统同调性的有效性，选择如图4的经典4机11节点系统进行测试。发电机采用经典二阶模型，负荷假定为恒阻抗，系统参数详见文献[26]。

图 4 典型4机11节点系统拓扑Fig.4 Typical topology of 4-machine 11-bus system

初始条件下网络参数与发电机模型严格按照母线8左右对称，调节负荷1为1.374+0.111j p.u.，负荷2为1.663+0.111j p.u.，故障设置为线路9—10末端三相短路，0.07 s后故障自动消失。仿真发现，(G1,G2)相对(G3,G4)为主要的同调分群。为获得不同同调性场景，调整G1，G2，G3动态模型参数以及线路7—8、线路8—9的长度，计算相应同调性指标I。该试验系统中，G1与G2、G3与G4的模型参数差异越大，该分群模式下系统同调性越差；线路7—8和线路8—9长度越短，系统同调性越差。部分仿真结果如表 3所示。

表3 4机11节点系统的非同调参数调整倍数及指标ITable 3 Non-coherent parameter adjustment multiples and index I of 4-machine 11-bus system

对应参数下系统的时域仿真曲线如图 5所示，随着 (G1,G2)相对(G3,G4) 对应动态等值系统的同调性不断下降，I从98.30%依次降低到45.81%。由图 5可知，文中所提指标I能有效反映系统发电机转子角轨迹的同调性。

图5 4机11节点系统非同调参数调整后的受扰轨迹Fig.5 Disturbed trajectory of 4-machine 11-bus system after adjusting the non-coherent parameters

为进一步验证文中同调性指标的有效性，选择同调性代表性指标S1与S2验证其有效性[17]，指标定义为：

(22)

(23)

式中：t为分析时段内任意时刻；tEND为终止时间；Δδi(t)=δi(t)-δi(0)为t时刻第i台发电机角度相对0时刻初值的变化量。

指标S1，S2分别利用一段时间内同群任2台发电机i,j角度变化量差值的最大值及其在研究时段内的累积量来评估系统同调性，指标越小则同调性越强。针对表 3中不同同调性场景，使用典型指标S1，S2验证文中所提指标的有效性，结果如表 4所示。由表4中算例1—算例3可知，I能准确反映G1与G2的非同调性变化。特殊地，对于算例4与算例5，当同调分群发生改变时，I依然能用于同调性量化评估。而传统指标S1与S2是基于多机角度的相对变化量，在分析不同算例同调性时存在一定的局限性。

表4 I的有效性验证Table 4 Validity verification of I

4.3 指标有效性探讨

同调性的定义依赖于动态等值的分群模式，仿真发现，一个分群模式同调性的降低可能意味着其他分群模式同调性的提高。传统的同调性评估方法一般针对给定分群，计算一段时间内角度差的最大值或差分量的积分，在多机系统中缺乏对全局同调特性的评估。文中同调性指标基于确定分群的惯量等值系统，具有明确的物理意义，能够量化分析同一分群模式下各发电机的同调程度，为动态等值的相关研究提供校验工具，未来有希望在此基础上提出有效的发电机同调分群辨识方法。

5 结语

文中根据电力系统单摆方程的周期特性，提出一种动态等值系统同调性的量化评估方法。当系统理想同调时，其动态行为的周期特性满足基于单摆方程推导的定积分表达式，结果的差异性越大，系统同调性越差。基于此，文中首先从动态等值系统的角度曲线中提取UBP和LBP的信息，结合微分方程特性实现了计及阻尼力矩影响的等值系统周期估算；随后通过估算周期与实测周期作差标幺化，提出发电机受扰轨迹同调程度的量化分析指标。在所提指标的基础上，分析了阻尼力矩对动态特性的影响，进一步提出系统阻尼特性的定量评估方法。周期与系统阻尼的估算在SMIB中得到验证，同调性分析在4机11节点系统得到验证。

这种基于轨迹的电力系统同调性量化评估方法，可广泛应用于大规模电网的动态等值校验，帮助解决静态或暂态稳定分析中系统降阶的有效性评估问题。文中方法的局限性在于,电力系统单摆方程推导忽略了复杂模型与控制器的影响，在实际系统中随着仿真时间或测量时段的延长，指标准确性不断下降。因此，文中指标仅可用于研究扰动后较短时间内(首摆或前几摆)的同调特性，不能用于系统同调性随时间变化的研究。