提升双馈风力发电系统低电压穿越能力的跟踪控制方法

王若谷，张若微，王明杰，高欣，秦博宇

(1.国网陕西省电力公司电力科学研究院，陕西 西安 710100；2.西安交通大学电气工程学院，陕西 西安 710049)

0 引言

伴随能源危机和环境问题在全球范围内的逐渐加重，以风能为代表的可再生能源在我国取得了长足发展。据最新公布的全国电力工业统计数据显示，2019年我国累计并网风电设备容量已经达到2.1亿千瓦，同比增长14%[1]。然而，大规模风电并网给电网安全稳定运行带来极大挑战，其中最为突出的是因风电场低压穿越 (low voltage ride through,LVRT) 能力不足导致的连锁脱网事故[2—4]。双馈风机 (doubly-fed induction generator,DFIG) 作为风力发电的主流机型之一，提升其LVRT能力对提高风电并网稳定性具有重大意义。

现有LVRT方案主要可以分为三类：加装硬件设备、换流器控制以及二者的协调配合。硬件设备主要包括：加装撬棒电路[5—6]、转子串电阻[7—9]、直流卸荷电路[10]及无功功率补偿装置[11]等。换流器控制主要包括转子侧换流器 (rotor side converter,RSC) 和网侧换流器 (grid side converter,GSC) 控制。文献[12]针对传统矢量控制的不足,改进了相应的换流器控制方案。文献[13]在PI控制的基础上，针对定子磁链出现的负序和直流分量制定了相应控制策略。然而，这类基于线性模型的控制器在严重故障扰动下无法保证良好的动态性能。文献[14]将微分几何理论应用于RSC的控制，提出一种基于精确线性化的非线性控制器，但其控制律的实现均较为复杂，不利于实际工程应用。文献[15]提出一种GSC低电压穿越控制策略，通过改变调制电压信号以达到抑制直流母线电压的目的，然而未对严重故障下直流母线电压的控制效果进行讨论。文献[16]设计了一种基于李雅普诺夫稳定判据的GSC非线性控制器，尽管能一定程度抑制直流母线电压波动，但可能无法保证双馈风机暂态期间的无功支撑能力。状态相关Riccati方程(state dependent Riccati equation,SDRE) 理论[17]为设计非线性暂态控制器提供了新的思路，文献[18]基于SDRE理论设计了一种RSC的非线性状态调节器，能在暂态期间调节状态变量至原平衡点附近，但受限于状态调节器的设计原理，无法主动调节暂态期间无功功率。

利用SDRE理论设计的非线性系统暂态控制器具有更强的灵活性和更大的稳定范围，并且实现方式更为简单。因此，文中提出一种基于SDRE理论的GSC跟踪控制方法，以进一步提升DFIG的LVRT能力。首先，以抑制外界干扰影响、维持故障期间直流母线电压稳定以及提供无功功率支撑为控制目标，建立GSC的控制问题。然后，利用SDRE理论完成上述问题的求解，获得状态反馈控制律。最后，将上述GSC控制配合DC chopper 保护电路构成完整的综合LVRT策略。

1 控制问题描述

GSC的结构如图1所示，可采用式(1)中的三阶动态模型进行分析。

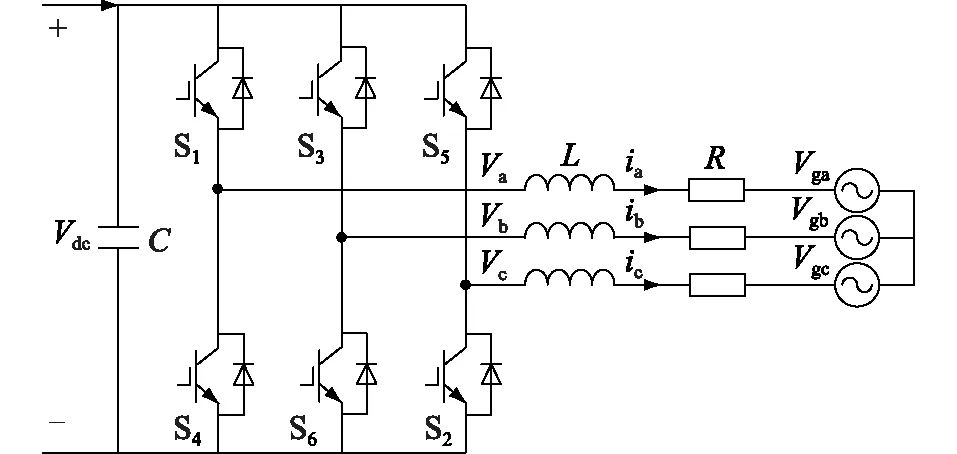
图1 双馈风机GSC的结构Fig.1 Structure of GSC in doubly-fed induction generator

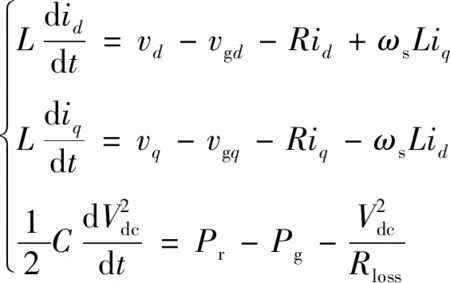
(1)

式中：vd,vq分别为GSC交流侧电压的d，q分量；id,iq分别为GSC输入电流的d，q分量；Vdc为直流母线电压；R，L分别为滤波器及进线电抗器的电阻和电抗之和；ωs为同步角速度；vgd,vgq分别为并网电压的d，q分量；C为直流母线电容器；Pg为GSC输出的有功功率；Pr为RSC输出的有功功率；Rloss为GSC的等效电阻。

将三阶模型式(1)转换为一般仿射非线性形式，并将平衡点移动至原点，如式(2)所示。

(2)

式中：x为受控系统的状态变量；f(x)为状态变量的函数；u为受控系统的控制变量；d为外界干扰；g1(x)，g2(x)分别为干扰和控制变量的系数矩阵。

(3)

(4)

u=[ΔvdΔvq]T

(5)

d=[ΔvgdΔvgqΔPr]T

(6)

(7)

(8)

从式(1)可以看出，GSC的状态变量存在相互耦合关系，并且呈现非线性的特征。

传统GSC的线性控制器通过引入电网电压扰动项和电流状态反馈进行前馈补偿，以达到解耦控制的目的。这种控制方法需要在平衡点处对状态方程线性化，因此在系统偏离平衡点较远时控制器不能完全反映系统的动态，难以保证其暂态控制有效。因此，为了降低外界干扰的影响，有必要设计一种考虑干扰抑制的非线性控制器。

非线性干扰抑制控制主要解决2个问题：第一，寻找一种控制策略，使在d=0时，GSC系统在x=0处渐近稳定；第二，当初始条件为x(0)=0时，这种控制策略使系统从干扰d到调节输出向量z的增益小于或等于给定的正数γ[19]，即：

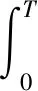
(9)

为了通过状态反馈控制律u将干扰d对输出的不利影响减少到一个足够小的程度，建立如下极大-极小微分对策问题。

(10)

式中：z(x,u)为调节输出，可根据实际控制目标选取；γ为抑制干扰的指标，γ越小代表干扰对输出带来的不利影响越小。上述问题的含义为：受控系统受到控制变量u和干扰变量d两类作用影响，形成一个对策问题，并且该对策必须满足如式(10)中的微分方程。

DFIG机端发生电压暂降时，将求解干扰抑制控制问题得到的状态反馈控制律u作为GSC的输出电压信号，此时GSC满足性能指标对控制变量极小和对干扰量极大，这意味着该控制律即为在最坏可能干扰d下的系统最佳控制策略。

GB/T 19963—2011[20]要求：当风电场并网电压跌落至0.2 p.u.时，风电机组应通过注入无功电流支撑电压恢复。而DFIG稳态运行时，GSC一般保持功率因数为1，存在一定的无功功率调节能力。为了进一步提高DFIG暂态期间的LVRT能力，GSC的暂态控制目标应为保证直流母线电压稳定和提供无功功率支撑，因此设计相应的跟踪控制器[21]实现上述目标。

输出跟踪控制器一般选取期望输出与实际输出的偏差作为调节量。结合控制目标，选择GSC无功功率以及直流母线电压作为关注的输出量。其中，GSC输出的无功功率可以表示为：

(11)

而直流母线电压可以表示为：

(12)

因此，文中选择调节输出z(x,u)为：

(13)

式中：z1为无功功率输出；z2为直流母线电压的平方；y1为期望无功功率变化量，可根据GSC的容量约束进行调整；y2为0表示希望暂态期间直流母线电压在平衡点处保持稳定；D(x)为控制变量u的权重矩阵，暂态期间可以选择D(x)作为期望与实际输出的偏差ez的衰减函数，从而达到平衡控制成本和控制效果的目的。

(14)

式中：m，n为可根据控制成本的考虑自由选择的常数。当偏差ez越大时，为了提升控制效果，需要此时控制输出越大越好，即选择权重矩阵越小。相反，当偏差ez趋于0时，意味着输出趋于期望值，此时可以适当降低控制输出，节约控制成本，即选择权重矩阵越大。

通过对式(10)极大极小微分对策问题的求解，可以获得状态反馈控制律u，实现维持故障期间直流母线电压稳定以及提供无功功率支撑的控制目标。然而，对于一个非线性系统而言，直接求解上述微分对策问题是非常困难的，为了解决这一问题，文中采用SDRE理论来进行近似求解。

2 干扰抑制控制律的求解

第1章已经构建了如式(10)所示的待求解的控制问题，在微分方程式(2)的约束下，求解状态反馈控制律u的优化控制问题本质上可以看作是带有约束条件的变分问题。这类问题通过极值原理最终可以转化为求解Hamilton-Jacobi-Issacs偏微分不等式[19]。求解过程如下：

(15)

其中Λ∈Rn为Lagrange乘子向量。

(2) 构造系统的Hamilton(H)函数。

H(x,Λ,d,u)=| |z| |2-γ2| |d| |2+
ΛT(t)[f(x)+g1(x)d+g2(x)u]

(16)

将z(x,u)代入(15)中，得到：

H(x,Λ,d,u)=ΛT(t)[f(x)+g1(x)d+

g2(x)u]+| |H(x)+K(x)u| |2-γ2| |d| |2

(17)

(18)

(19)

式中：Vx为一个非负函数V(x)的梯度向量，且V(0)=0；r(x)=KTK，为非奇异矩阵。Vx为哈密顿-雅可比-伊萨克斯(Hamilton-Jacobi-Issacs,HJI)不等式，即式(20)的解。

(20)

所求暂态控制律则可根据式(20)得到，该控制律即为干扰抑制控制律。对于非线性系统，HJI不等式(20)缺乏解析解的通用求解方法，但是对于线性系统而言，上述问题可以通过Riccati不等式方便地求解。SDRE理论将仿射非线性系统的状态方程在平衡点处拓展线性化，形成含有状态相关(state dependent coefficient，SDC)矩阵的类线性结构，从而通过求解状态相关Riccati方程获得原系统的状态反馈控制律。

2.1 SDRE理论简介

SDRE理论由于其控制灵活、设计简单的特点，已在飞行器设计、无人机控制等领域得到应用[22]。通过拓展线性化，SDRE理论能将一般非线性系统的状态方程转化为状态相关的类线性形式。对于含有多状态变量的受控非线性系统，非线性项的分解存在无穷多种，其对应的系统动态响应也存在差异，这为优化SDRE控制器提供了额外的自由度[23]。非线性系统在经过拓展线性化之后可以看作一个随状态变量时刻变化的线性系统。在每个采样时刻，A(x)，B1(x)，B2(x)，C(x)和D(x)均可看作根据当前状态变量而确定的常数矩阵。

(21)

其中，

(22)

用上述状态相关矩阵代替不等式(20)中的f(x)，g1(x)，g2(x)，H(x)，K(x)，可以看到此时HJI不等式转变为式(23)所示的不等式，该不等式也被称作状态相关Riccati不等式。

(23)

2.2 GSC控制器设计

GSC的状态方程(2)经过上述变换后可以表述为式(21)所示的形式。其中，A(x)表达式为：

(24)

根据SDRE理论，在每个采样时刻都可以对状态相关Riccati不等式(23)进行求解，由式(13)、式(19)和式(23)可以推导出GSC的状态反馈跟踪控制律[17]，可表述为：

(25)

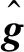
(26)

在实际应用中，实现SDRE技术的主要计算量在于每个采样时刻对代数Riccati不等式的求解。需要说明的是，随着嵌入式处理器的快速发展，已有大量采用SDRE技术进行实时控制的实际案例[24—26]，实时求解的计算量已经不再是影响SDRE实际应用的问题。

3 综合LVRT策略

GSC跟踪控制和DC chopper保护电路的协调配合共同构成了DFIG综合LVRT策略，具体流程如图2所示。

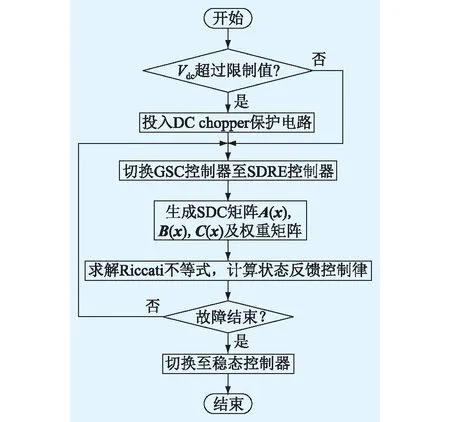
图2 综合LVRT策略流程Fig.2 Flow chart of comprehensive LVRT strategy

在故障初期，并网电压突然降低，由于定子磁链不能突变，产生的定子磁链直流分量在转子侧感应出暂态电动势并导致转子电流骤增，最终造成直流母线过电压。此阶段的直流母线电压很难直接用GSC控制完全抑制，因此，投入DC chopper保护电路来降低转子过电流从而抑制直流母线过电压。与此同时,切换GSC的稳态控制至暂态SDRE控制。根据3.2节中的方法，在每个采样时刻生成SDC矩阵以及权重矩阵，求解对应的Riccati不等式，由式(25)和式(26)计算状态反馈控制律并将调制后的信号送至RSC直至暂态过程结束。最后，当并网点的电压恢复至故障前附近水平时认为故障结束，此时切换为原稳态控制，至此完成双馈风机LVRT全过程。

4 算例分析

在Matlab/Simulink仿真平台中的单机无穷大(single machine infinite bus，SMIB)系统中进行仿真测试，验证所设计的综合LVRT策略在系统遭遇故障时的有效性。SMIB系统的结构如图3所示。

图3 SMIB系统结构Fig.3 Structure of the SMIB system

双馈风电场(包含6台1.5 MW DFIG)的详细参数见Matlab/Simulink R2019b中的detail模型。风速设置为15 m/s。t=2 s时，在25 kVⅡ处设置三相接地短路故障，接地电阻为2 Ω，故障持续时间为625 ms。故障期间GSC分别采用PI控制、精确线性化控制[10]与SDRE控制，仿真结果见图4—图6。

图4 并网电压Fig.4 Voltage of point of common coupling

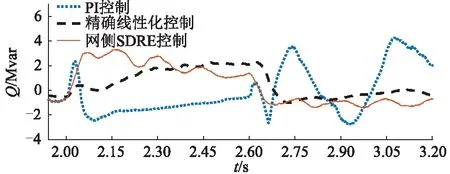
图5 DFIG输出无功功率Fig.5 Reactive power output of DFIG

图6 直流母线电压Fig.6 DC link voltage

从图4可以看出，在发生三相短路故障后，采用PI控制的风电场其并网电压已经跌至0.16 p.u.附近，采用精确线性化控制的风电场其并网电压在暂态期间逐步抬升，而采用网侧SDRE控制的风电场其并网电压在故障初始即可抬升至约0.2 p.u.。其原因在图5中体现：故障发生瞬间，采用PI控制的风电场只在初期短暂提供了一定无功功率，然后无功输出迅速下滑并全程处于吸收无功的情形，无法满足双馈风力发电系统LVRT的要求；而采用网侧SDRE控制的风电场在故障发生后能持续保持较高无功功率输出，从而支撑故障期间的电网电压。同时，故障结束后，采用PI控制的风电场无功出现较为明显的波动，而采用精确线性化控制、网侧SDRE控制的风电场无功过渡更为平滑。如图6所示，严重故障下采用PI控制的风电场其直流母线电压发生骤增，峰值甚至达到1 500 V，采用精确线性化控制的风电场虽然能够一定程度上抑制直流母线电压骤增，但是直流电压并不平稳，出现振荡现象。而采用网侧SDRE控制的风电场则有效抑制了直流母线电压的波动。另一方面，采用PI控制的风电场其直流电压的调节时间过长，约0.27 s后才稳定在平衡点附近，这可能会导致直流电容过充损坏，甚至威胁换流器的正常工作。综上所述，文中所设计的综合LVRT策略能够满足故障期间双馈风电场对LVRT的要求。

5 结语

文中提出了一种基于状态相关Riccati方程技术的GSC跟踪控制方法，并设计了DFIG的综合LVRT策略。为实现DFIG在电网电压跌落的情况下连续运行不脱网并提供一定的无功支撑，建立了GSC干扰抑制控制问题。根据相应的控制目标设计了GSC跟踪控制器，并应用SDRE理论获得状态反馈控制律。为进一步抑制电网电压下降初期的直流过电压，采用DC chopper保护电路协调配合网侧SDRE控制降低转子暂态过电流的影响。在SMIB系统中进行仿真测试，结果表明，文中所设计的综合LVRT策略能够在严重电网故障下较好地维持直流母线电压的稳定，并且能充分利用GSC的无功调节能力为电网提供一定的无功功率支撑。

本文得到国网陕西省电力公司科技项目(B626KY190005)资助，谨此致谢！