重磁数据的重加权正则化共轭梯度法约束反演

吴昊天,李 军,b,王堃鹏,b,李 霞

(成都理工大学 a.地球物理学院，b.教育部地球探测与信息技术重点实验室，成都 610059)

0 前言

重磁勘探作为地球物理勘探中的一种常用方法，它是根据地下目标体与围岩的密度或磁性差异引起的重磁场的空间变化，解决某些地质问题的一种勘探方法。重磁反演是重磁勘探解释工作中的重要内容，但由于重磁位场的“趋肤效应”和体积效应明显，其间接观测手段也决定了重磁反演问题多是不适定问题，导致了重磁反演存在现实困难和技术瓶颈。

重磁物性反演过程本质是求解大型欠定型线性方程组，计算效率和求解过程的稳定性和解的非唯一性是重磁物性反演的主要技术瓶颈。计算效率目前主要通过大型并行计算和改进矩阵计算和储存方式加以克服，而求解的稳定性和非唯一性问题则主要是通过先验约束和算法实现。B.J.Last[1]提出的紧密反演算法方法，就是在反演迭代的过程中加入最小体积这一先验信息，作为一约束条件，这一方法能够让结果异常体边界更加尖锐，物性分布更加集中，对整块地质体有较好的反映；Valeria Cristina F.Barbosa等[2]也提出了先加入先验信息的反演算法，这种方法对于轴线性的目标体有较强的分辨能力；Li等[3]所提出了最光滑反演方法，通过在反演算法中加入模型的最小梯度这一先验信息，作为约束条件，能够让异常体的边界缓慢过渡，也可以较好地反映目标体的空间位置；Oleg Portniaguine等[4]提出了聚焦反演算法，可以让异常体边界更加明显。Li 和 Oldenburg以及Pilkington[3,5-6]在反演算法中引入物性深度函数加权和光滑矩阵的约束，一定程度克服了反演目标的趋肤效应。Fedi等[7]对三维位场数据进行反演计算，解决了因为核函数随深度增加而递减造成的趋肤效应；Fedi等[8]针对通过SVD和GSVD方法对反演过程中的深度分辨率的问题进行分析；Fedi[9]中提出了DEXP方法，通过极值点预测异常体的深度，这是一种快速且稳定的方法；Cella[10]应用构造指数作为加权函数的参数来抵消核函数随深度的衰减。

显然，先验约束和算法改进能有效克服密度反演的不稳定性和非唯一性。然而，有效建立先验约束，并在算法上寻求优化协作，保证两者能贯穿整个反演求解过程，充分改进其计算的稳定性和结果的可靠性，仍是一个难点。

共轭梯度反演方法具有计算速度快、内存需求少，能够避免大型矩阵的乘积计算的特点，已成为大规模计算的实用反演方法。近年来预条件共轭梯度法和重加权共轭梯度法也被应用在位场数据反演中[11-15]。笔者试图在目标函数中加入约束项以及深度加权函数，利用基于PRP公式的重加权正则化共轭梯度法进行求解，期望能有效改进大型欠定方程的求解效率与精度和重磁物性反演结果的可靠性。

1 正演理论

重磁正演效率决定了重磁异常反演效率及其实用性。多面体构建的复杂重磁模型在重磁反演过程人机交互过高，其可操作性和实用性较差。这里设计基于网格剖分的模型构建和重磁异常正演计算，即对地下半空间进行规则剖分，剖分的每个规则六面体单元都赋予以密度值或磁化强度值(图1)。

地面某一观测点的响应可根据地下每个剖分单元的重磁场计算结果进行累加。剖分单元的重磁异常可采用直立长方体表达式计算：

Δg(x,y,z)=-Gσ(ξ-x){Ln[(η-y)+r]+(η-y)Ln[(ξ-x)+r]

(1)

(2)

若不考虑剩磁的作用，则：

k1=2MN,k2=2NL,k3=2ML,

k4=L2,k5=M2,k6=-N2，

L=cosIcosD,M=cosIsinD,N=sinI

式中：Δg(x,y,z)为某观测点地下长方体单元引起的重力异常;ΔT(x,y,z)为某观测点地下长方体单元引起的磁异常;G为常数;μ0为真空磁导率;σ为密度;M为磁化强度;I为磁倾角;D为磁偏角;(ξ;η,ζ)为剖分单元体积微元的中心坐标;(ξ1,ξ2,η1,η2,ζ1,ζ2)为地下长方体单元的角点坐标位置;r为长方体单元到观测点距离。

地表某点的观测数值与地下各剖分单元其物性参数所产生的场值呈线性关系：

Gm=d

(3)

其中：

(4)

图1 长方体单元模型Fig.1 Rectangular unit model

式中：G为N×M阶的核矩阵;其元素gi,j表示第i个测点由第j个剖分单元产生的场值;m为求解模型向量，共有M个模型;d为观测数据向量，共有N个观测数据。

2 约束反演理论

2.1 深度加权

由于重磁场具有“趋肤效应”特征，即趋于地表的地质体对观测点处所观测的重力异常权重较大，而离地表较远的地质体对观测结果影响较小，故反演物性会反映到更敏感的浅部，结果基本趋于地表，这会导致反演结果与实际情况相差较大。Li和Oldenburg[3,5]提出在反演过程中引入一个深度加权函数进行约束，能有效克服了重磁场随深度呈指数衰减的特征。这里采用这一深度加权函数：

(5)

式中：z为剖分单元的中心点埋深；z0取决于观测面位置；β为深度加权因子。根据重磁场随深度的衰减规律，一般在重力反演中取2.0，磁异常反演中取3.0。

2.2 光滑约束

在三维重磁线性反演，模型变量参数远远大于采集数据，所以反演往往是欠定的问题，则必须要在目标函数中加入模型约束项，以约束所求得解的范围。笔者引入光滑约束函数，其意义在于使得相邻的模型之差最小，使模型在各个方向上是光滑过渡的。定义模型粗糙度R为模型m在X、Y和Z方向的一阶偏微分的平方和，即：

(6)

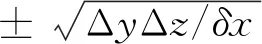
此时进行深度加权以及光滑约束下的模型约束项为：

(7)

其中

(8)

令：

(9)

式(7)中：Z为深度加权函数组成的对角矩阵；D为模型约束矩阵；as、ax、ay、az为光滑权重。

2.3 构建正则化目标函数

根据Tikhonov正则化理论，可以建立正则化目标函数来避免反演中出现的多解性问题。正则化目标函数包括两部分：①约束稳定函数;②数据拟合函数。为了抵消核函数的“趋肤效应”，增大其垂向分辨率，用深度加权函数对核矩阵进行改造，则有以下线性关系：

GZ-1Zm=d

(10)

令：

Gw=GZ-1

(11)

mw=Zm

(12)

可得到目标函数的数据拟合函数式(13)与约束稳定函数式(14)。

(13)

(14)

因此，正则化目标函数表达式为式(15)。

(15)

2.4 正则化因子的选取

在Tikhonov正则化反演过程中，正则化因子体现了数据拟合与模型约束之间的取舍与平衡。当正则化因子较大时，会优先进行模型约束，正则化因子过大可能造成无法拟合数据。当正则化因子较小时，会优先拟合数据，正则化因子过小可能会造成无法对模型约束，使得反演结果无法可靠反映地下的模型分布。

一般采用经验选取法、广义交叉验证法和L-curve法选择正则化因子。经验选取法凭借经验选取正则化因子具有较强的主观性。广义交叉验证法选取正则化因子包含了大规模矩阵的多次运算，L-curve法需要进行多次的反演运算才能选择合适的正则化因子。后两者的计算大，增加了计算成本。

笔者选取了一种自适应的正则化因子的选择方法，选择随一定步长下降的正则化因子[11]。令μ0=0，计算出经过初次迭代后的模型量，再使用式(16)计算出首个的正则化因子。

(16)

每次迭代后根据式(17)计算正则化因子。

μk+1=qμk，k=1,2,…,n

(17)

式中，q通常取0.5～0.9。根据式(16)与式(17)计算正则化因子。随着迭代次数的增加，正则化因子减小，能够优先拟合模型而后对数据进行拟合，保证了反演的稳定。该选取正则化因子的方法与广义交叉验证法以及L-curve法比较，有效地减少了计算量，达到了正则化因子自适应的目的。

2.5 基于PRP公式的重加权正则化共轭梯度法

共轭梯度法用迭代替代了大型矩阵的乘积与矩阵求逆的过程，加快了反演求解速度。在反演中使用传统的共轭梯度算法，进行界限约束或改变正则化因子时都需要重构残差，对算法进行“重启”。该情况下的共轭梯度算法便会退化为梯度下降法，降低了收敛速度与稳定性。笔者采用的是重加权正则化共轭梯度法，可以实现每次迭代都改变权重，以配合自适应的正则化因子，实现了数据拟合与模型约束的权重的动态变化。保证了约束质量的情况下加快收敛速度。

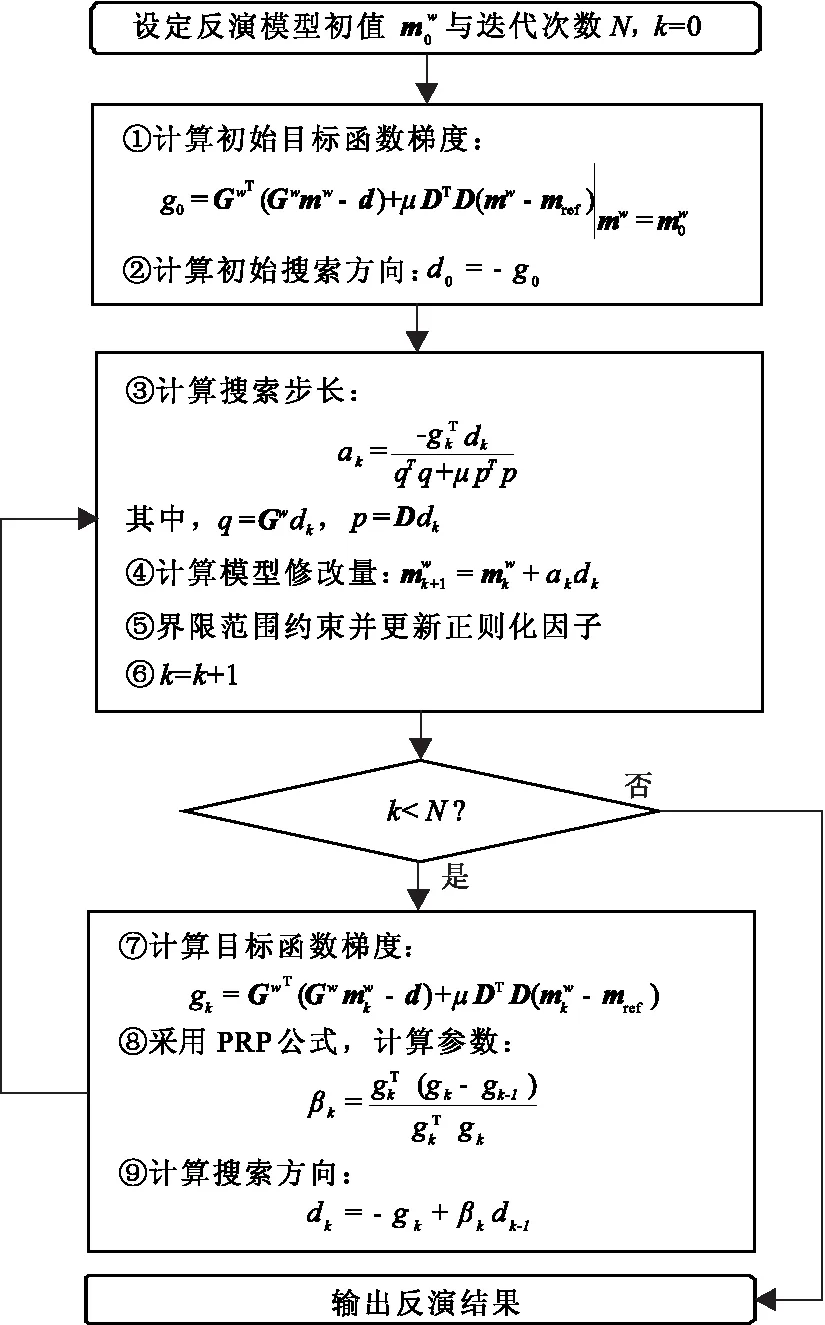
图2 基于PRP公式的重加权正则化共轭梯度算法流程图Fig.2 RRCG based on PRP formula

2.6 稀疏矩阵的优化储存

每个光滑约束矩阵中仅存在±C、0三种数值(C取值见本文2.2部分)，在剖分数量大时，若将该矩阵储存下来将会占用大量内存，加上核矩阵后，将会储存(N+4M)×M大小的矩阵，对如此大的矩阵进行乘积运算将耗费大量的计算时间。

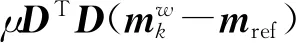
(18)

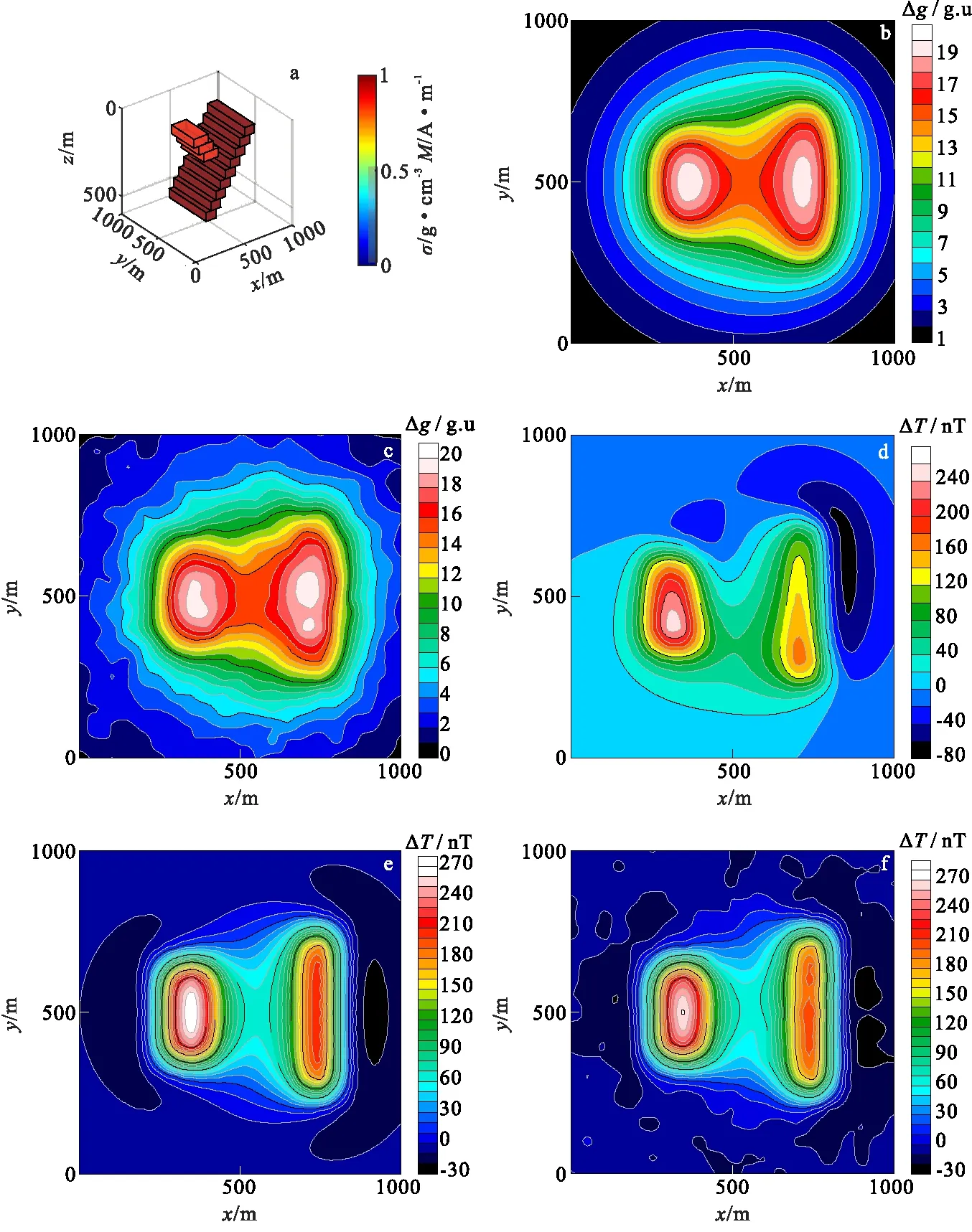
图3 正演模型以及噪声污染的正演数据Fig.3 The forward model and the forward data contaminated by noise(a)三维模型示意图；(b)重力异常正演数据；(c)噪声污染的重力异常正演数据；(d)磁异常正演数据；(e)磁异常垂直磁化数据；(f)噪声污染的磁异常数据

图4 不同公式下的重力反演与磁反演相对拟合差变化图Fig.4 The relative misfit of different formulas in gravity inversion and magnetic inversion(a)重力反演下不同公式的相对拟合差变化图；(b)磁反演下不同公式的相对拟合差变化图

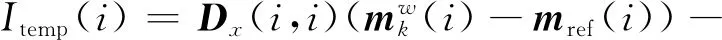
(19)

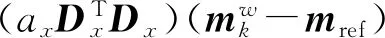
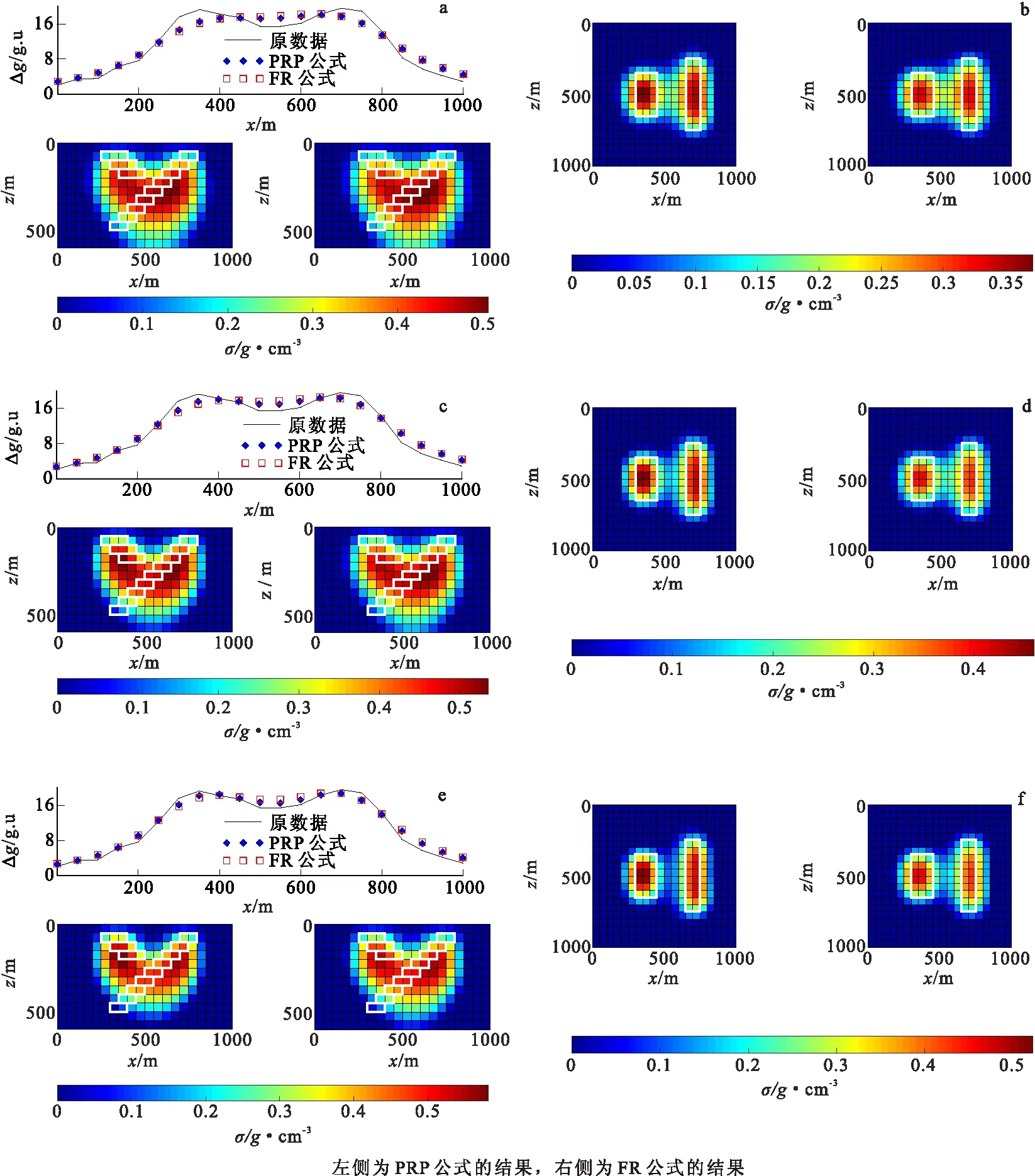
图5 不同迭代次数下的磁反演结果Fig.5 Magnetic inversion results under different iteration times(a)迭代60次y=525 m处剖面；(b)迭代60次z=125 m处截面；(c)迭代80次y=525 m处剖面；(d)迭代80次z=125 m处截面；(e)迭代100次y=525 m处剖面；(f)迭代100次z=125 m处截面

3 模型反演

笔者引用了姚长利等[13,17]使用过的Y型岩脉模型。如图3所示，左侧异常体I剩余密度为0.8 g/cm3，磁化强度为0.8 A/m，向下延伸至200 m。右侧异常体II剩余密度为1g / cm3，磁化强度为1 A / m，向下延伸至500 m，二者磁倾角皆为45°，磁偏角皆为45°，而反演时只考虑垂直磁化情况下的数据。将地下三维空间剖分为20×20×12=4 800个单元，其边长为50 m。共有21×21=441个采集数据，数据采集点位于z=0处。在观测数据中，加入了5%的高斯噪声污染(图3(c),图3(f))，以测试反演针对实测数据的能力。反演的物性参数范围控制为0 g/cm3～1 g / cm3与0 A/m～1 A/m。

迭代100次，重力反演花费时间为8.593 s，磁反演花费时间为9.135 s，其中因为磁异常公式复杂，计算核矩阵的时间花费较多。

重力反演与磁反演在PRP公式与FR公式下的相对拟合差随迭代次数的变化曲线如图4所示。

图6 不同迭代次数下的重力反演结果Fig.6 Gravity inversion results under different iteration times(a)迭代60次y=525 m处剖面；(b)迭代60次z=125 m处截面；(c)迭代80次y=525 m处剖面；(d)迭代80次z=125 m处截面；(e)迭代100次y=525 m处剖面；(f)迭代100次z=125 m处截面

表1 重力反演的相对拟合差Tab.1 The relative misfit of different formulas in gravity inversion

表2 磁反演的拟合差Tab.2 The relative misfit of different formulas in magnetic inversion

由图4可以看到，在重力反演与磁反演中，分别迭代40次与16次之后，PRP公式开始低于FR公式下的相对拟合差，且相对拟合差保持稳定下降的趋势。

表1和表2为重、磁反演于PRP公式与FR公式下不同迭代次数的相对拟合差变化表。当迭代次数较小时，FR公式下的相对拟合差略微小于PRP公式下的相对拟合差。随着迭代次数的增加，PRP公式下的相对拟合差逐渐小于FR公式下的相对拟合差。反映该模型下PRP公式下的反演计算具有较高的收敛速度和计算效率。

如图5与图6所示为加入噪声的重力异常数据和磁异常数据在PRP公式和FR公式下分别进行60次、80次和100次的反演迭代结果。总体而言，重力反演以及磁异常反演在加入噪声的情况下能够在一定程度上的反映异常体的位置以及形态，没有出现过拟合的现象。

由于深度加权对核函数进行了改造，反演计算中的模型量是由深部向浅部移动的，所以在收敛慢的情况下，模型量在深部聚集的更多。

对于重力反演，与FR公式相比，PRP公式下的反演剖面浅部位置的模型量能够更快迭代得到，异常体形态相对更加紧凑，模型底界面深度较为可靠。对于地下截面，PRP公式下的反演结果，分辨率相对较高，边界刻画更加明显，且模型量更接近实际模型的值。同时，PRP公式下的数据拟合结果更加接近原始数据。所以PRP公式在该模型下的重力反演有着较快的收敛速度和更高的计算精度。

图7 马角坝3号地质剖面磁异常图Fig.7 Magnetic anomaly map of geological section no.3 of Majiaoba

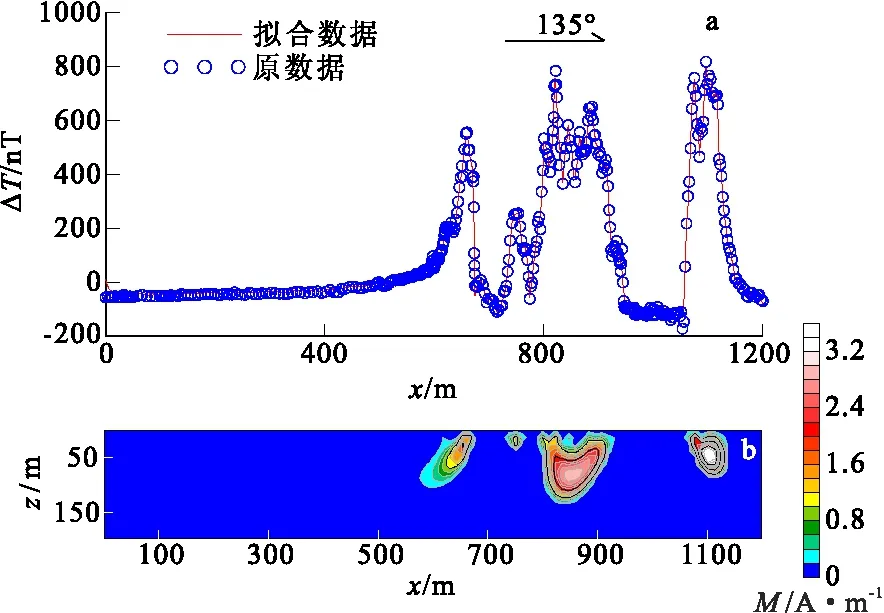
图8 马角坝3号地质剖面磁异常磁化强度反演图Fig.8 Inversion map of magnetic anomaly magnetization in geological section No.3 of Majiaoba(a)数据拟合结果；(b)反演结果

在磁反演中，与FR公式相比，PRP公式下的反演剖面，其浅部与深部模型分布更加合理。FR公式中的结果中，其异常体I下方聚集的模型量较大且恢复的模型在垂向上的形态宽大。对于地下截面，在迭代60次之下，PRP公式的结果中反映的模型量稍大，更加接近真实值。而在迭代80次与与100次时，二者的结果并没有很明显的差异，且出现了少量因为噪音而产生的模型分布，但可以忽略不计。同时，PRP公式下的数据拟合与FR公式下的数据拟合结果，稍微更接近原始数据曲线，但差别较小。则PRP公式在该模型下的磁反演同样有着较快的收敛速度和较高的计算精度。

对比重力反演与磁反演结果，对于y=525 m处剖面，由于异常体I较为宽厚，且异常体II在深部延伸至异常体I之下，由于等值现象，在重力反演以及磁异常反演的结果中，均有左侧模型量较右侧模型量大的结果出现，且在磁异常反演中因为异常体II延伸至异常体I之下，抵消了部分异常体I的负异常，导致反演出的磁化强度偏大且聚集。二者在深部反演的结果也有一定程度向下延伸，呈现光滑过渡的形态。对于z=125 m处截面，由于磁异常数据本身的较高分辨率，且因磁反演的深度权重较重力反演大的影响，磁异常反演的结果更加紧凑，分辨率较好。

从二者整体反演结果来看，反演结果基本与Y型岩脉一致。在浅部的形态相对于深部的清晰，但反演结果不可避免地随着深度下降而降低分辨率。经以上讨论表明：

1)基于PRP公式的重加权正则化共轭梯度的约束反演能够在一定噪声干扰下从一定程度上反映地下物性分布情况，相对FR公式有较高的计算效率和计算精度。

2)在重磁反演结果对比中，由于磁异常数据较为复杂，相邻紧密的模型异常等效作用更明显，会存在南北极耦合及正负异性抵消的情况，而重力数据这种情况表现相对较弱。

3)由于磁异常数据本身的分辨率更高，且其深度权重较大反演能够得以较快地收敛，其反演结果的分辨率更高。

4 实际资料应用

成都理工大学马角坝实习基地地质3号线自火焰包到灌林包，长约1 200 m，地处龙门山系前山带的边缘。在三叠纪末的印支运动中，受西北造山带造山作用的影响，全区褶皱上升成陆，结束海侵。在由西北向东南推挤的应力作用下，本区地层形成轴向北东的褶皱和一系列北东向延伸、向西北倾斜走向的逆冲断层和与之配套的近南北向和北西西方向的平移断层。同时伴有小规模的岩浆沿断裂或裂隙侵入，形成辉绿岩墙。

高精度磁测异常表明地质线路上在飞仙关二段有明显的磁异常，标本测量揭示该段地层粉砂质泥岩的磁化率最大可达100×10-5(SI)，相对其他地层有较明显的磁性，可引起50 nT～100 nT以上的异常。但结合本次测量，可以注意到在飞仙关二段的整体异常高达600 nT～800 nT，这说明该地质线路的高磁异常并非完全由飞仙关二段地层引起。

笔者利用该条磁测剖面进行了三维磁化强度反演，设计正演网格模型为240×41×40个单元，其网格单元边长为5 m。共有400个采集数据。采用重加权正则化共轭梯度法约束反演，迭代150次，耗时26 min 35 s，得到如下异常(图8)的反演结果与拟合结果。

反演结果表明测线下方飞仙关二段地层存在明显的局部地质体，其磁化强度最高可达3.5 A/m，这一磁化强度显然不是该沉积地层的响应。但我们注意到该测线的三个主要异常，有两个异常的倾向于地层倾向角度近似(北西倾向45°～57°)，故初步判断该异常可能为后期沿断裂侵入的局部辉绿岩墙。但由于该区后期构造改造复杂，使得该区地层出现大量的倒转褶皱，并在倒转翼上发生冲断层或逆断层，使得部分侵入岩体与地层倾向存在明显差异，如图8中的最南东部的异常。

5 结论

针对重磁异常反演的趋肤效应的问题，采用深度加权函数约束；针对重磁物性参数反演的不适定问题，建立了基于光滑约束的正则化目标函数。利用基于PRP公式的重加权正则化共轭梯度法约束反演，完成了复杂模型的重磁数据的反演效果评价，并通过实际资料的应用，论证了算法理论的有效性和可靠性，得出以下结论：

1)使用了基于PRP公式的重加权正则化共轭梯度法，改善了重磁反演的计算效率和计算精度，动态调整正则化因子，降低了运算成本，达到自适应正则化因子的目的；

2)根据模型反演，PRP公式下反演得到的剖面、截面、数据拟合曲线和相对拟合差曲线相对于FR公式下的反演结果有相对优势。

3)对比重磁反演结果，磁异常的分辨率略优于重力异常，这一方面与磁异常模型数据本身具有较高分辨率有关外，还可能与反演中磁异常深度权重的相对较快收敛作用有关。