例析隐零点问题的三类处理技巧

魏东升

(江西省瑞金第一中学 342500)

函数与导数主要是考查学生逻辑推理、直观想象和数学运算等核心素养的主要载体，其一直是高考考查的重点之一.在处理函数与导数的压轴题时，对零点的处理往往是一个关键环节，有些函数的零点确实存在，但无法精确求解，此谓之“隐零点”；有些导数的零点虽然可求，但因含参而需要讨论.对于这类问题，常见的处理方式主要有虚设零点、化隐为显和变换主元三大类.

一、虚设零点

所谓虚设零点，是指为了处理函数的隐零点问题，通过采取假设函数零点却不直接求解，通过谋求整体的转化,将函数转化为易求的形式进行求解的一种处理技巧.

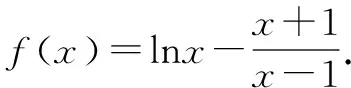
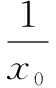
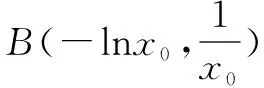
评析本题涉及了超越函数(指数函数、对数函数和三角函数等函数结合的函数)，在假设零点后，可以考虑把超越式(如lnx、ex等)分离出来再代入表达式求解，以达到将超越函数转化为普通函数的目的，此谓之整体消“超”．除此之外，对于一类函数零点个数判断(或根据零点个数求参、或零点所在区间判断)的问题，可以考虑利用该零点附近的特殊点的函数值来确定符号，谓之特点定号(如2019年全国Ⅱ卷文)；对于含有参数的函数，还可以考虑整体消参(如2019年天津卷文)和降次留参(如2019年江苏卷)等方式，

二、化隐为显

所谓化隐为显，指的是为了避免出现直接求导带来的隐零点问题，通过采取重新构造函数的方式，把隐零点转化为显零点的一种处理技巧.

例2 (2017年全国Ⅱ卷理)已知函数f(x)=ax2-ax-xlnx，且f(x)≥0．求a．

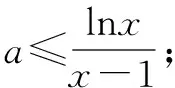
评注分离是化隐为显的一种常见手段，其通常用于分离参数，或者是分离含有类如xlnx这样的超越式.本题中除了分离参数，还由于f(x)含有xlnx而导致求导后出现了隐零点问题，故而采取了将x和lnx分离的处理方式.除了分离构造，常见化隐为显的方法还有合并构造(如2018年全国Ⅱ卷理)、放缩构造(如2018年全国Ⅰ卷文)和双雄构造(指把一个函数拆成两个函数，如2014年全国Ⅰ卷理)等.

三、变换主元

有些数学问题中常含变量，在某些情况下为了解决问题的需要，可人为地突出该变量的主体地位作用，将之当作主元构造新的函数，以达到化难为易的目的.这种思路还适用于多元变量函数的问题.

例3 (2015年全国Ⅰ卷文)设函数f(x)=e2x-alnx.

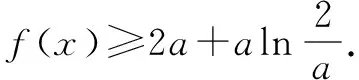
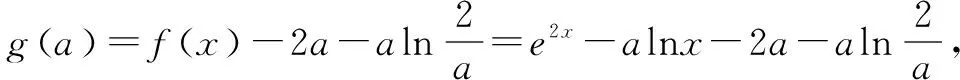
当a<2ex时，g′(a)<0；当a>2ex时，g′(a)>0，所以a=2ex时，g(a)取最小值为g(2ex)=e2x-2ex.

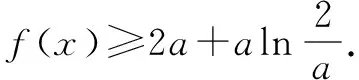
评注本题如果直接对f(x)进行求导，会出现隐零点问题以致给解题带来不便，故这里采用了重新构造关于变量a的对数超越函数的处理方式.除了重构对数超越函数，变换主元往往还会重构指数超越函数(如2016年全国Ⅲ卷文)、重构双勾型函数(如2017年全国Ⅲ卷文)和重构二次函数(如2019年浙江卷).

通过上述几个高考真题我们知道，通过结合已知条件和结论虚设零点、化隐为显和变换主元是解决隐零点问题的主要处理策略．在导数压轴题的教学过程中，像这样以专题的形式介绍隐零点问题的处理策略，尽量一次性彻底地解决与其有关的问题，对学生解题水平的提升、逻辑思维的训练和核心素养的培养，想来都是极好的．