探究问题本质 提高解题能力——以一类二元二次方程的研究为例

李昌成

(新疆乌鲁木齐市第八中学 830002)

最近在教学过程中遇到一个问题，教师看起来挺容易，但是学生觉得很困难.在我所带的实验班中正确率才8%，几乎全军覆灭.于是，我对此类问题进行了深入探究.现分享与此，以飨读者.

一、试题呈现

题目方程2x2+xy-y2-4x+5y-6=0表示( ).

A.一个圆 B.两条平行直线

C.两条相交直线 D.不确定

在和学生交流中发现，学生根本无从下手，仅能根据圆的一般方程排除A.至于后面三个选项更趋向于D，我哭笑不得.学生普遍反映不知道方程左边该怎样处理.

二、解法探究

首先，我请同学们一起观摩了参考答案：

由于2x2+xy-y2-4x+5y-6

=(2x-y)(x+y)-4x+5y-6

=(2x-y)(x+y)+2(x+y)-6x+3y-6

①

=(x+y)(2x-y+2)-3(2x-y+2)

②

=(2x-y+2)(x+y-3)，

所以根据(2x-y+2)(x+y-3)=0，得

2x-y+2=0，或x+y-3=0.

据此判断原方程表示两条相交直线，故选C.

这个解法遭到了同学们的普遍质疑：①处的2(x+y)是怎样想到的？②的公因式2x-y+2是偶然的，还是必然的？①中能否去拼凑2x-y呢？这种解法具有一般性吗？调整系数还可以这样分解吗？

在学生急切期盼中，我给学生分析解答如下：

基于2x2+xy-y2=(2x-y)(x+y)，说明

2x2+xy-y2-4x+5y-6=(2x-y+m)(x+y+n).

③

否则，关于x，y的一次项和常数项没有来源.

下面用待定系数法求解m，n.

(2x-y+m)(x+y+n)

=(2x-y)(x+y)+n(2x-y)+m(x+y)+mn

=(2x-y)(x+y)+(2n+m)x+(m-n)y+mn.

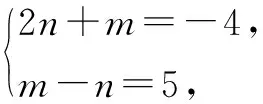
所以2x2+xy-y2-4x+5y-6=(2x-y+2)(x+y-3).

殊途同归，学生基本接受了，他们认为这种解法可以复制.事实上，这类题目有个大前提：前三项齐次式必须可以分解，否则这种办法搁浅.

三、本质探究

设二元二次方程为ax2+bxy+cy2+dx+ey+f=0(abc≠0)其中a=a1×a2，c=c1×c2，b=a1c2+a2c1.

于是ax2+bxy+cy2+dx+ey+f=(a1x+c1y)(a2x+c2y)+dx+ey+f.

令ax2+bxy+cy2+dx+ey+f=(a1x+c1y+m)(a2x+c2y+n)=(a1x+c1y)(a2x+c2y)+n(a1x+c1y)+m(a2x+c2y)+mn=(a1x+c1y)(a2x+c2y)+(na1+ma2)·x+(nc1+mc2)y+mn,

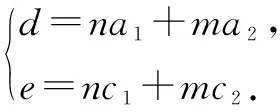
至此，我们把这一类二元二次方程ax2+bxy+cy2+dx+ey+f=0(其中a=a1×a2,c=c1×c2,b=a1c2+a2c1)问题本质理清了.它表示的两条相交直线是：

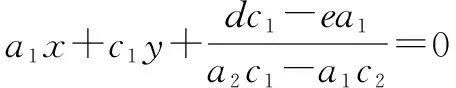
四、拓展延伸

我们知道，平面上两条直线的位置关系有相交、平行、重合三种.既然两条相交线可以有这样的表示方式，那么两条直线平行、重合又该如何表示呢？

两条平行直线的方程可以分别表示成：ax+by+c1=0和ax+by+c2=0(a2+b2≠0).那么仿照前文可知，它们可以用一个方程表示为

(ax+by+c1)(ax+by+c2)=0.

④

整理，得

(ax+by)2+a(c1+c2)x+b(c1+c2)y+c1c2=0.

⑤

逆向思考可知⑤表示两条平行的直线.这里尤其需要注意：④式中两因式变量系数对应相等；⑤式中两个一次项系数与二次项系数、常数项的关系.

例1方程x2+4xy+4y2+3x+6y+2=0表示____.

解析因为x2+4xy+4y2=(x+2y)2，所以x2+4xy+4y2+3x+6y+2=0可以变形为(x+2y)2+(1+2)x+2(1+2)y+1×2=0.

即(x+2y+1)(x+2y+2)=0.

所以x2+4xy+4y2+3x+6y+2=0表示两条平行直线x+2y+1=0和x+2y+2=0.

同理，两条重合的直线表示为(ax+by+c)2=0.

即a2x2+2abxy+b2y2+2acx+2bcy+c2=0.

例2方程x2+2xy+y2+2x+2y+1=0表示____.

解析因为x2+2xy+y2+2x+2y+1=(x+y+1)2，所以x2+2xy+y2+2x+2y+1=0表示两条重合的直线x+y+1=0，也可以看成一条直线.

五、牛刀小试

练习方程2x2+3xy+y2+5x+3y+2=0表示____.

解析因为 2x2+3xy+y2=(2x+y)(x+y)，两个因子的x，y系数不成比例，所以2x2+3xy+y2+5x+3y+2=0表示两条相交直线.

由前文知a1=2，a2=1，c1=1，c2=1，d=5，e=3.

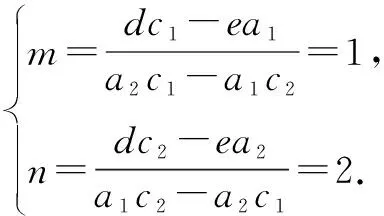
所以2x2+3xy+y2+5x+3y+2=(2x+y+1(x+y+2).

所以方程2x2+3xy+y2+5x+3y+2=0表示两条相交直线2x+y+1=0和x+y+2=0.

六、教后反思

1.教学中务必注重通性通法教学，学生方可“复制”

所谓通性通法是指具有某种规律性和普遍意义的常规解题模式和常用的数学解题方法.建构主义认为,教学应以使学生形成对知识的深刻理解为目标.《普通高中数学课程标准(实验)》也指出:“高中数学课程应该返璞归真,努力揭示数学概念、法则、结论的发展过程和本质.”《2020年数学科考试说明》也指出:“数学知识考查时,要从学科整体意义和思想含义上立意,注重通性通法,淡化特殊技巧,要有效地检测考生对中学数学知识中所蕴含的数学思想和方法的掌握程度.”因此,数学教学应重视对通性通法的深层次理解,强化基础知识、基本技能的训练,深入理解数学的本质,发展数学应用意识,提高实践能力.只有学生掌握了通解通法，才不可能短时间就“忘了”，才能做到举一反三，灵活应用，避开题海战术，并且提升能力.

2.教学中，比答案更重要的是揭示问题本质

高中学生学得辛苦,但由于缺乏对数学问题本质的认识,常常事倍功半,在重复与茫然的训练中效率不高．因此,教师的指导作用应该体现在“讲清数学道理,揭示数学本质”上．通过教师自身或集体研究,帮助学生反思学习过程、领悟数学背景,从数学知识的根源开始,理清每一类问题的来龙去脉,使得数学知识“拎起来成一串、撒下去铺一片”,这样才能让学生真正学懂弄通,学习和应试都不再迷茫．

3.适当拓宽教学内容，扩大学生视野，激发学习兴趣

我们知道，现行初中教材中，因式分解只介绍了提公因式法和公式法.事实上，因式分解有很多方法，但是初中学生精力有限，为了减负，没有全面铺开，同时也是教材编写的原则：螺旋上升.但是到了高中，我们需要更多的因式分解方法以应对各种复杂的问题.此时我们有必要做好拓宽补充工作，否则学生跟不上教学节奏，听不成课，做不成作业，学习积极性会受到创伤.

另外，二元二次方程在高中现行教材中仅在《圆的一般方程》一节提到过，也没有详细介绍.但是圆、椭圆、双曲线、抛物线都是它的特例，在大学中还会深入全面研究它.在高中教学过程中有机会给学生适度引入介绍，增加一些了解，对学生来说，不仅从知识的层面有收获，更重要的是可以激发学生的求知欲，对数学充满期望，对未来的大学学习也是一个铺垫.何乐而不为呢！