求圆锥曲线最值问题的三种思路

张彩玲

(安徽省砀山中学 235300)

一、利用三角函数的有界性

三角函数的有界性是当x∈R，那么|sinx|≤1,|cosx|≤1，这就是三角函数的有界性，也是三角函数的重要性质之一，在求解圆锥曲线问题时，利用三角函数的有界性，通常能帮助我们将复杂问题简单化.

例1已知圆的方程为x2+y2-4x-10y+25=0，该圆与直线l相切，又与直线x=2，y=5构成面积最小的三角形，求直线l的方程.

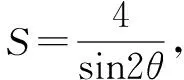
解析将原方程进行配方，得

(x-2)2+(y-5)2=4.

设x′=x-2,y′=y-5，那么新坐标下的圆的方程为x′2+y′2=4.

直线x=2、y=5分别是新坐标系中的x′轴和y′轴，原点就为(0，0).

设切点为(2cosθ,2sinθ)，那么切线方程为

2x′cosθ+2y′sinθ=4.

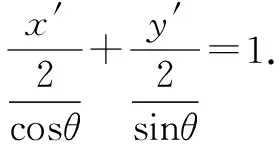
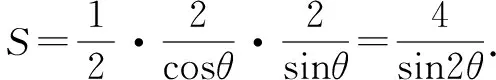
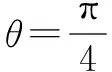
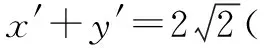
二、利用导数法

利用导数法求圆锥曲线极值问题，首先得构造与所求量有关的函数关系式，然后再通过对构造的函数f(x)进行求导，令导函数f′(x)=0，求出极值点x值，再根据定义域从而确定所求量的极值.

例2已知抛物线为x2=2py(P>0)，存在一定点M(p，p)，求在抛物线上存在点Q，使得|MQ|2最小.

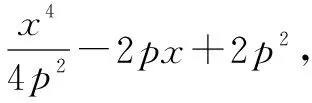
解析设点Q的坐标为(x，y)，则

|MQ|2=(x-p)2+(y-p)2.

令f(x)=|MQ|2

=x2-2px+p2+y2-2py+p2

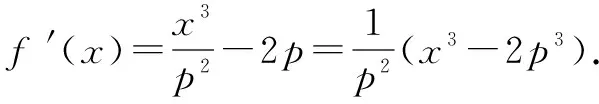
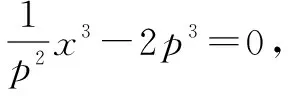
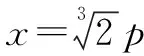
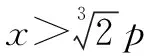
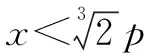
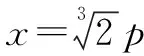
三、利用基本不等式法

基本不等式法是指两个正实数的算数平均数大于或者等于它们的几何平均数.也可以说，对于任意实数a和b，存在这样一个关系：a2+b2≥2ab，那么当且仅当a=b时，等号成立.

例3已知抛物线y2=4x与x2=4y，两抛物线在第一象限内的公共点为点A，过点A作一条直线，使该直线与x轴和y轴的正半轴所围成的三角形的面积最小，求该三角形最小的面积.

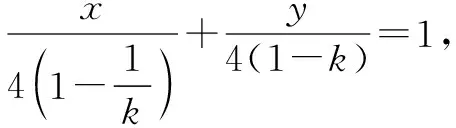
解析联立方程并且根据第一象限的性质，可得到点A的坐标为(4，4).

将通过点A所引出的直线的斜率设为k，则k≠0,k≠1.

通过点斜式的公式，得y-4=k(x-4).

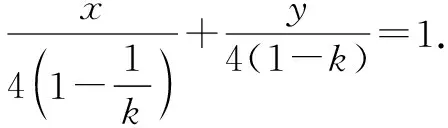
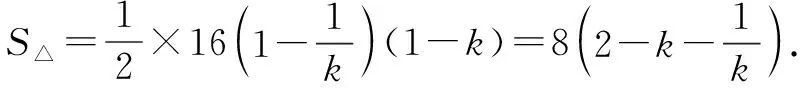
又因为两个截距都为正，

所以k<0，

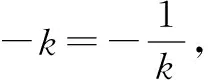
由以上几个例题发现，圆锥曲线最值问题，容纳了各种各样的解题技巧，与其他知识点相互渗透，不仅要求学生对解题技巧掌握得十分熟练，而且还要学会灵活运用.希望在以后的解题过程中，能发现更多的解题方法，并将这些方法进行整理，这样对于提升成绩大有益处.