变加速直线运动问题解法分析
福建 姚龙楷
物体所受合外力的方向与速度方向在同一条直线上,物体做直线运动。如果合外力发生变化,那么物体的加速度可能是大小发生变化,也可能是方向发生变化,还可能是大小方向均发生变化,从而引起物体运动过程中速度大小、方向的变化,进而物体的位移大小、方向发生一系列变化。变加速直线运动问题的物理情境和过程较为复杂,是学生学习的难点。本文试着对此类运动问题整理分析,给出解决此类问题的一些思路,以期能对读者起到一定的启迪作用。
一、分析受力情况,明确运动过程
清楚分析物体的受力情况,是解决变加速直线运动问题的第一步,要明确:当合外力的方向与物体运动方向一致时,即加速度方向与速度方向相同,合外力的作用效果是推动物体运动,物体做加速运动;当合外力的方向与物体运动方向相反时,即加速度方向与速度方向相反,合外力的作用效果是阻碍物体运动,物体做减速运动。
【例1】如图1所示,一木块静止在光滑水平面上,在恒力F的作用下向右运动,其正前方固定有一劲度系数足够大的弹簧,当木块接触弹簧后,下列关于木块说法正确的是
( )
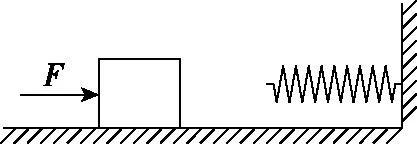
图1
A.立即做减速运动
B.立即做匀速运动
C.在一段时间内速度继续增大
D.当弹簧处于最大压缩量时,木块的加速度不为零
【解析】木块与弹簧接触前,水平方向仅受恒力F作用而向右做匀加速直线运动,木块与弹簧接触后,弹簧被压缩而产生弹力,由于弹力作用,使木块的加速度减小,但速度继续增大,直到弹力与恒力F的大小相等时,速度达到最大,C选项正确,AB选项错误;木块继续向右运动,这时弹簧的弹力已经大于恒力F,木块加速度方向变为向左,开始做减速运动,随着弹簧压缩量的继续增大,木块的加速度继续增大,而速度减小。当弹簧压缩量达到最大时,木块水平向右方向的加速度达到最大,D选项正确。
【点评】此类问题的基本分析思路是:力→加速度→速度。即物体受到的合外力决定物体的加速度,加速度决定单位时间内速度的变化,而与物体的瞬时速度无关。本题中由于弹簧弹力是变力,物体做变加速运动,务必要做好受力分析,逐步分析其运动过程,分析清楚弹簧的形变量、弹力、加速度如何变化,以便对运动情况作出正确的判断。
二、找准特殊点,简化过程分析
在很多物理问题中由于存在变力作用,导致物体的加速度不断变化,使得这类问题复杂化。若把分析匀变速直线运动问题的思路移植到变加速直线运动问题中,则容易出现失误。此时仔细寻找物体运动过程中的一些特殊点,将是解决这类问题的关键。
【例2】如图2所示,水平固定的小圆盘A均匀带电,带电荷量为Q,电势为零,从小圆盘中心处O点释放一质量为m,带电荷量为+q的小球,由于电场力的作用,小球竖直上升的最大高度可达到圆盘中心竖直线上的C点,OC=h1。又知过竖直线上B点时小球速度最大,已知重力加速度为g,由此可确定
( )
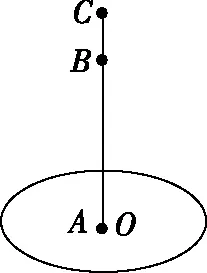
图2
A.B点的场强 B.C点的场强
C.B点的电势 D.C点的电势
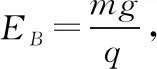
【点评】分析变加速直线运动的关键集中在特殊点的分析上,比较常见的有初始位置、平衡位置(加速度为零)、速度最小(常常为零)的位置,如本题的C点。速度最大(加速度为零)的位置,如本题的B点。只有研究好各个特殊点,才能正确全面地分析物体的运动过程,才能合理地选取过程,应用相应规律予以解决。
【例3】如图3所示,一个质量m=0.1 g,电荷量q=4×10-4C带正电的小环,套在很长的绝缘直棒上,可以沿绝缘直棒上下滑动。将绝缘直棒置于正交的匀强电场和匀强磁场内,E=10 N/C,B=0.5 T。小环与棒之间的动摩擦因数μ=0.2。求小环从静止沿棒竖直下落过程中的最大加速度和最大速度。取g=10 m/s2,小环电荷量不变。
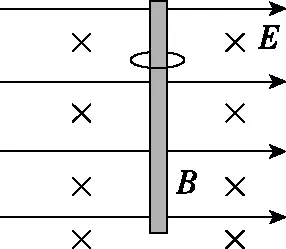
图3
【解析】开始时,小环速度为零,小环受重力mg、水平向右的电场力F=qE,由于绝缘直棒固定,绝缘直棒给小环的弹力FN与电场力F平衡,即FN=qE。小环向下滑动,受到摩擦力为Ff=μFN=μqE。已知mg>μqE,所以,小环将加速下滑。
小环加速下滑过程,受水平向右的洛伦兹力F洛=qvB,因而弹力FN、摩擦力Ff都将相应地增大,根据牛顿第二定律mg-μFN=ma可知小环的加速度减小,小环做加速度减小的加速运动,于是洛伦兹力F洛、弹力FN、摩擦力Ff又将随之增加,小球的加速度继续减小。当小球的加速度减为零时,速度达到最大值。
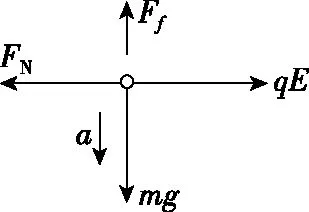
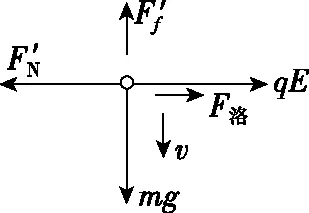
分析小环竖直方向的受力情况,由牛顿第二定律得mg-μFN=ma,即mg-μ(qE+qvB)=ma。
当v=0时,即刚下落时,小环运动的加速度最大,代入数值得am=2 m/s2。
当a=0时,下落速度v达到最大值,代入数值得vm=5 m/s。
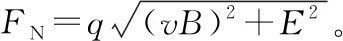
【变式二】若本题其他条件不变,只是磁场方向改为垂直纸面向外,小环运动后,受到洛伦兹力的方向改为水平向左,与电场力方向相反,于是杆对小环的弹力FN将减少,当qvB=qE时,FN=0,因而Ff=0,小环的加速度增大到g,自此以后小环速度再增加,会使qvB>qE,弹力FN从零变为FN=qvB-qE,直到FN增大到使μFN=mg,小环运动稳定,有μ(qvmB-qE)=mg。
【点评】小环速度的变化,引起洛伦兹力、弹力、摩擦力的变化,小球加速度的变化,最终又反过来引起速度的变化,这是带电体在磁场中运动所具有最突出的特点。分析时,应以速度对洛伦兹力的影响为线索来讨论其他力的变化特征。
三、应用动量与能量观点,优化解题过程
变加速直线运动的物体受到的合外力是变力,若利用高中的数学知识,沿着牛顿第二定律F合=ma为主线列方程,将会遇到极大的困难,所以我们要利用动量与能量观点来解决相应问题。
【例4】如图4所示,两根彼此平行的光滑金属导轨水平放置,其间距为L,导轨的左端与一光滑绝缘的曲面相切,在水平导轨上距切点x处垂直于导轨静置一质量为m、电阻为R1的金属棒P,水平导轨处于磁感应强度大小为B、方向竖直向上的匀强磁场中。现从曲面上距底端高h处静止释放一质量也为m、电阻为R2的金属棒Q,该金属棒将沿曲面下滑并滑上水平导轨。设运动过程中两金属棒始终保持平行并与导轨良好接触,导轨足够长且不计电阻。
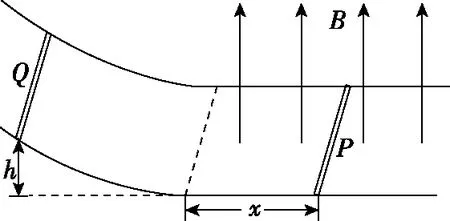
图4
(1)求运动过程中金属棒P所能获得的最大加速度;
(2)当x满足什么条件时,可保证两金属棒在运动过程中始终不相碰;
(3)求整个过程中损失的机械能。
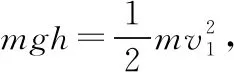
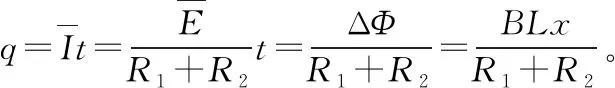
【例5】如图5所示,挡板P固定在足够高的水平桌面上,小物块A和B大小可忽略,它们分别带有+QA和+QB的电荷,质量分别为mA和mB,由绝缘的轻弹簧相连,一不可伸长的轻绳跨过滑轮,一端与小物块B连接,另一端连接一轻质小钩。整个装置处于场强为E、方向水平向左的匀强电场中。小物块A、B开始时静止,已知弹簧的劲度系数为k,不计一切摩擦及小物块A、B间的库仑力,小物块A、B所带电荷量保持不变,小物块B始终不会碰到滑轮。
(1)若在小钩上挂一质量为M的小物块C并由静止释放,可使小物块A对挡板P的压力恰为零,但不会离开挡板P,求小物块C下降的最大距离;
(2)若小物块C的质量改为2M,则当小物块A刚离开挡板P时,小物块B的速度多大。
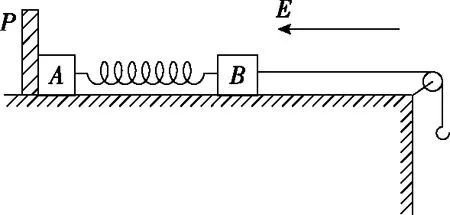
图5
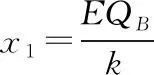
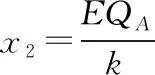
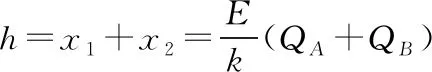
(2)由能量守恒定律可知,小物块C下落h过程中,小物块C重力势能的减少量等于小物块B电势能的增加量和弹簧弹性势能的增加量以及系统动能的增加量之和。当小物块C的质量为M时,Mgh=QBEh+ΔEp④
当小物块C的质量为2M时,设小物块A刚离开挡板时小物块B的速度为v,则有
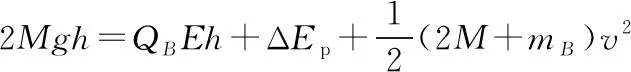
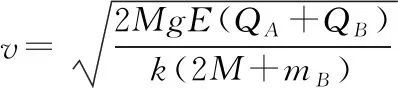
【点评】在高中不涉及弹簧弹力做功表达式的问题,在用到弹性势能时,一般是通过弹簧形变量相同时(如伸长量和压缩量相同)弹性势能也相同来处理。本题中,挂上小物块C后,小物块B在电场力及弹簧弹力作用下做变加速运动,小物块C下降过程绳子拉力是变力,所以,用牛顿第二定律难以解答,而应用动量与能量观点可以回避运动过程分析,从而使解题过程达到最优化。
【总结】对于变加速直线运动的分析,具体步骤如下:首先,分析物体的受力情况,利用牛顿第二定律判断物体加速度的方向;其次,由加速度方向与初速度方向的关系判断物体是加速运动还是减速运动;再根据运动过程中物体受力情况判断加速度如何变化,物体做什么性质的运动;最后,根据运动过程的特点,选用恰当的规律解决问题。

