基于差分进化和核主元分析的燃气轮机故障检测

李汶骏， 龙 伟， 曾 力

(1.四川大学机械工程学院, 成都 610065； 2.重庆交通大学机电学院, 重庆 400074)

1 引 言

燃气轮在工作期间始终处于高温、高压、高速、高负荷、振动等极端环境中，并且随着工业技术的不断发展，燃气轮机系统的结构越来越复杂，而作为飞机的心脏，航空燃气轮机的状态检测和健康管理对飞行的安全、提高运行使用效能和经济性有着重要作用，因此迫切需要探索高效、准确的燃气轮机异常状态检测手段.航空燃气轮机故障检测技术可分三种类型：基于模型的故障检测技术、基于数据驱动的故障检测技术和基于知识规则的故障检测技术.其中基于数据驱动的故障不需要真实设备或复杂的数学模型[1]，在燃气轮机这类复杂系统中得到广泛应用[2-3].

KPCA算法作为一种核学习算法，将数据通过映射反映到高维空间提出特征，可用于处理具有非线性特性的数据.目前在国内外的复杂非线性系统故障检测领域都得到广泛应用，也经常出现在缺陷预测、图像处理等领域中[4-5].

文献[6]通过建立一种自适应监测统计量(AT2)，提高了KPCA对非线性故障检测的自适应性.文献[7]提出了一种改进的核主成分分析法(LKPCA)，将局部结构分析集成于传统KPCA诊断方法中，实现了对TE故障集的更精确诊断.文献[3]用核主元分析法实现了对燃气轮机部件故障的诊断，并通过对故障敏感性的定量分析实现了故障定位.文献[8]针对燃气轮机参数的时变特性产生的假故障率高的情况，提出一种用动态控制限KPCA进行监测的航发异常监测方法.

传统KPCA故障检测算法一般选择单核核函，周卫庆等人[9]用高斯核主元分析实现了对大型热力系统的故障检测.但单核KPCA不能满足故障数据的复杂特征，通过不同核函的线性组合可以实现不同特征映射能力的有效集成，混合核KPCA成为研究热点，张珂等[10]通过线性组合方式建立混合核主元分析模型，使用二分法大致确定核参，用TE故障数据集验证了可行性证明其故障检测能力优于单核.考虑到多个参数取值对核函数的复杂耦合影响，核参数选择不当会使算法泛化能力降低，出现欠拟合或过拟合，无法使KPCA发挥最大作用，本文提出基于差分进化算法优化的核主元分析法，将多项式核函同径向基核函线性结合得到混合核函，同时引入差分进化算法，以检测率为目标，对混合核函中的核参数、权重比进行优化，实现核函数最优参数的确定.并且通过实验证明，本文方法可以准确寻找到最优的核参数、权重比，有效提高燃气轮机气路系统异常状态检测率.

2 KPCA故障检测

2.1 KPCA 方法

通过非线性映射函数Φ(·)将原始输入空间xi映射到高维映射空间，经中心化处理后的变换向量为φ(xi)，i,j=1,...,N.

设中心化处理后的非线性变换输入数据矩阵如式(1)所示.

Φ=[φ(x1),φ(x2),...，φ(xn)]T∈Rn×f

(1)

f是高维空间维数，则核主元分析过程如下[11]：

(1) 建立核函数矩阵.

(2)

式中Ki,j=K(xi,xj)；K(·)为核函数.

(2) 对核函数矩阵KΦ中心化处理后进行特征值分解.

(3)

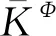
(3) 取a个主元代替n个自变量.主元数量的选取与主元模型的准确性直接相关，为明确选取变量数量，定义主元贡献率δi、前a个主元累积贡献率ηa.

(4)

(5)

通过式(4)衡量主元ti对n个变量所包含信息的贡献份额，通过式(5)衡量前a个主元所包含的信息量占总信息量比重，一般累计贡献率需80%以上.

(4) 建立主元模型.将第(3)步选取的a个主元相对应的特征向量v1,v2,…,va进行正交化处理，得到单位正交特征向量p1,p2,…,pa，然后计算核主元，如下式.

(6)

最后建立主元模型，即

(7)

2.2 建立故障阈值

在完成原始数据KPCA变换后，本文通过统计学方法建立阈值以进行故障检测[12]，计算其主元模型的T2和SPE统计量的控制阈，通过检测采集数据的两个统计量，判断其是否超限，来确定航空燃气轮机是否发生故障，其故障检测步骤如下.

(1) 建立正常工作情况下数据集的主元模型，并将其中心化、标准化处理.

(2) 计算服从自由度为a和n-a的F分布，置信度为α的T2统计量控制上限，如式(8)所示;检验水平为β的SPE控制上限，如式(9)所示.

(8)

a为确定主元个数，通常取α=0.01；

(9)

(3) 采集i时刻在线实时数据，中心化、标准化处理得Xi∈R1×m.

(4) 提取i时刻在线实时数据的非线性主元ti.

(5) 计算该时刻数据的T2和SPE统计量，判断是否超限.

3 基于DE优化的KPCA故障检测

3.1 混合核函的定义

在利用KPCA算法进行故障检测过程中，核函数、核函数的核参数选择都直接影响到检测效果.常见的核函数有多项式型核函、高斯径向基型核函、Sigmoid型核函，其中多项式核函是全局核，函数作用范围广，即当输入数据集的变化范围较大时，该函数仍能保持较高的敏感性，利于提取输入数据集的全局特征，缺点是容易被噪音干扰；高斯径向基核函是局部核，输入数据集变化越大，对特征提取的影响越小，核参数决定了该函数的影响范围，因此具有较高的抗干扰能力，缺点是核参数对该核函的性质影响大.以上两函数优缺点能够很好的互补，也是最常用的两种核函数[13].

为了使核函数能够发挥最优效果，本文采用将多项式核函(全局核)和高斯径向基核函(局部核)进行线性组合生成的混合核函并用DE(差分遗传算法)对上述参数及权重比进行优化，得到效果最优的故障检测模型.

多项式核函：

Ki,j=[x(i)·x(j)+1]d

(10)

高斯径向基核函：

(11)

混合核函：

Ki,j=(1-ρ)[x(i)·x(j)+1]d+

(12)

检测率函数：

(13)

式中，d是多项式核函阶次，d∈[1,5]；ρ是混合函数的权重系数，ρ∈[0,1]；σ是高斯径向基核函的宽度；n为总检测试验样本个数；nT为其中检测结果正确的样本个数；检测率函数f∈[0,1].

3.2 差分遗传算法优化

通过上节描述，本文将KPCA故障检测转化为一个拥有3个优化参数的最优化问题模型.随后引入差分进化算法(DE)[14-15]解决问题，DE算法是一种随机的启发式算法，利用随机偏差扰动产生新个体的方式，获得较强的鲁棒性，引导搜索结果达到全局最优.将差分进化算法引入KPCA故障检测中，其核参数优化过程的步骤如下.

Step1：定义差分进化算法的必要参数

种群数量:NP=200；

自适应变异算子：F=F0·2λ；

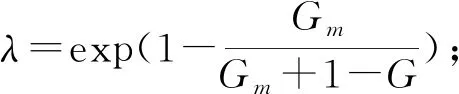
F∈[0,2]，此处取F=0.5.

交叉算子：CR=0.1；

最大进化代数：100.

Step2：在取值范围内随机产生初代种群，令第一代k=1.

Step3：通过式(18)确定检测率函数f，对初始种群进行评价.

Step4：在k为最大进化代数时停止循环，输出此时种群中最佳个体，否则继续.

Step5：进行交叉变异，同时对边界条件进行处理，得到临时种群，计算其检测率函数，进行评价.

Step6：对临时种群、原种群中个体进行“一对一”选择，得到新种群，此时进化代数k=k+1，转到Step 4.

最后，基于差分进化优化的混合核KPCA故障检测流程图如图1所示.

图1 混合核KPCA故障检测流程图Fig.1 Flow chart of fault detection of mixed kernel KPCA

4 实验验证

为验证基于差分进化优化的核主元分析故障检测方法的可行性和优越性，将该方法用于双轴涡喷燃气轮机气路部件故障进行验证并与传统KPCA故障检测方法进行比较.航空燃气轮机作为一种复杂精密的热力机械，满足功率平衡、热平衡等一系列条件.因此当故障发生时，其传感器测量的气动参数也会立刻产生变化，可以用来反映发动机的性能状态变化，通过对诸如温度、压力、转速等气路性能参数的有效分析，可以实现对航空燃气轮机故障的检测[16].

本文使用Gasturb燃气轮机总体性能计算软件进行故障仿真[17]，该软件可以通过对健康参数的调节实现对非设计点的各气路参数计算，其数据具有时变性、强耦合、非线性等特点.以双轴涡喷发动机为例验证文中方法的有效性，其结构图如图2所示.主要结构包含低压压气(LPC)、高压压气机(HPC)、高压涡轮(HPT)、低压涡轮(LPT)、高压轴(N1)、低压轴(N2)、燃烧室(Bunner).

气路部件的故障可大致分为流通能力蜕化、效率蜕化，分别以流量系数φ、效率系数η来表征.燃气轮机中装有许多传感器用以监测运行情况，需要选择适合的参数来完成对既定目标的检测[18]，本文对双轴涡喷的传感器监测参数选择如表1所示.

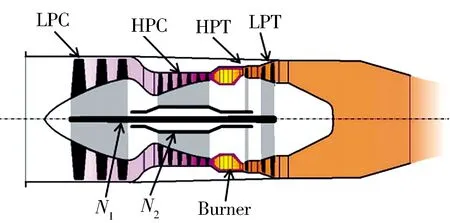
图2 Gasturb双轴涡喷发动机结构图

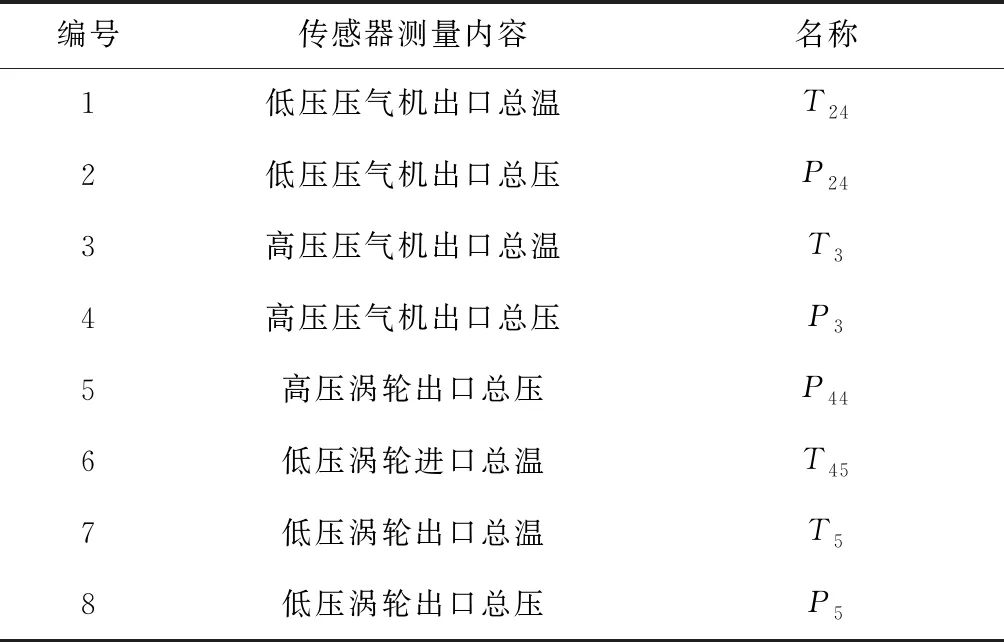
表1 双轴涡喷发动机监测参数选择

设定飞机工作状态：飞行高度10 km，马赫数为1.4 Ma.收集正常工作时的测量参数建立主元模型，计算统计量阈值.

在发动机正常工作到第50组数据后，通过给初始低压压气机流量系数φ0、效率系数η0添加衰退因子，实现对低压压气机衰退或故障的模拟，定义如下式.

φΔ=φ0-Δφ，ηΔ=η0-Δη

(18)

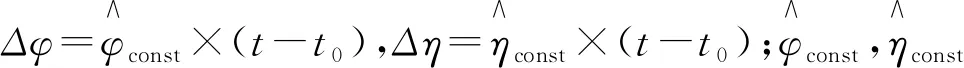
以SPE作为主要参考统计量，选取0.85的主元贡献率，来验证故障检测率.经过多次实验，确定高斯径向基KPCA有效核宽度取值区间为σ=[3,261]，在此区间外的检测模型均失效，选取核参数σ几个具有代表性的值时对应的故障检测率，见表2.

表2 径向基KPCA对双轴涡喷发动机的检测率

由表2可知，当σ=5时，径向基KPCA对双轴涡喷发动机的气路故障检测率达到最高，为0.94；多项式KPCA在核参数d取不同值时对应的故障检测率值，见表3.

表3 多项式KPCA对双轴涡喷发动机的检测率

图3 最优参数寻优过程图

由表3可知，当d=4时，多项式KPCA对双轴涡喷发动机的气路故障检测率达到最高，为0.92.以上是传统的核参数人工选择方法.

接下来，按照图1流程建立混合核KPCA故障检测模型，使用差分进化算法进行优化，其核参数寻优过程如图3所示.

由图可知，通过差分进化算法对核参数的不停迭代，最终在第54次得到能使异常状态检测率达到97%的混合核KPCA检测模型.三种KPCA检测模型的最优检测率，见表4.

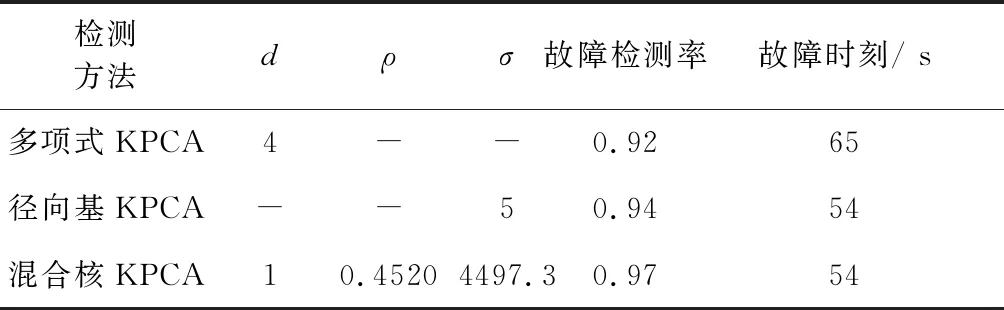
表4 三种方法对双轴涡喷发动机的检测率

通过表4可知，优化后的混合核KPCA检测率要高于多项式KPCA检测率、高斯径向基KPCA检测率，证明本文所研究检测模型能够解决复杂非线性耦合影响下核参数的取值问题，完成科学最优取值，并且实现对燃气轮机异常状态故障的准确检测，且检测率高于其他传统核方法.

根据最优混合核KPCA的核宽度σ、核参数d取值与其余两种检测方法对应核参均不同，可证明不同核函的核参数取值对混合核函特征提取效果具有复杂耦合关系，传统独立的选取各核函最优值来达到整体最优效的方法不可靠.

三种核方法对应的检测图，分别如图4～图6所示.其中，折线是不同采样时刻燃气轮机工作的监测值，直线表示燃气轮机正常工作的安全阈值.

图4 多项式KPCA对航发异常状态的检测图

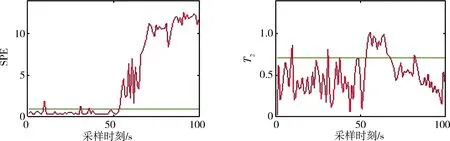
图5 径向基KPCA对航发异常状态的检测图

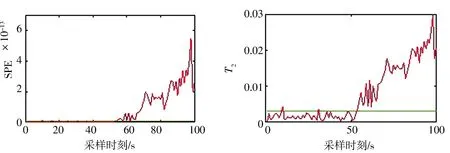
图6 混合核KPCA对航发异常状态的检测图

从图4～图6中可以看出，三种方法均能准确检测出双轴涡喷燃气涡轮气路系统发生的故障.结合表4可知，多项式KPCA的统计图在65 s之后才完全超过阈值，对故障的响应较慢；高斯径向基KPCA的SPE图在进行到72 s后失去对故障漂移特性的描述、其T2在故障发生后多次回到阈值，检测失效.

而混合核KPCA在故障发生后能迅速检测出其漂移特性，证明经差分进化优化的混合核KPCA相较传统方法能更好的提取故障数据的特征，对航空燃气涡轮发动机气路故障检测具有更高的敏感性、准确性.

5 结 论

本文通过对传统KPCA故障检测算法中混合函数的参数优化，利用差分进化遗传算法建立了优化混合核KPCA故障检测模型.通过对双轴涡喷发动机气路异常故障进行验证，主要结论为：(1)证明了混合核函中不同核函数的核参对检测效果存在耦合影响，并针对传统KPCA故障检测算法中核参数难以精确取值的问题，提出了基于差分进化遗传优化的方法，使检测模型能够更好提取故障特征，证明了其检测率优于传统径向基、多项式KPCA故障检测方法；(2) 针对航空燃气轮机这类复杂非线性系统.本文建立了基于DE和KPCA的燃气轮机气路故障检测模型，不依靠数学模型，只需要正常运行数据，且检测率高、对故障敏感，具有较高的实用性.