一类带时变系数的退化抛物系统的奇性
胡 丽, 樊明书
(西南交通大学数学学院, 成都 610031)
1 引 言
在本文中, 我们研究以下的方程组:
(1)
其中Ω⊂Rn是一个光滑有界区域,m,n>1, 系数k1(t),k2(t)是关于t>0的正连续函数. 我们假设非线性项f1(v),f2(u)满足f1(v)>0,f2(u)>0,f1′(v)>0,f2′(u)>0,(u,v>0),f1(0)=f2(0)=0,且初值u0(x),v0(x)是非平凡的非负连续函数, 在边界∂Ω上为零.
自上世纪60年代以来, 很多学者对非线性抛物方程的整体解和爆破进行了研究[1-6].如,2007年Payne等[7]研究了带Dirichlet边界条件的下述半线性抛物问题
ut=Δu+f(u), (x,t)∈Ω×(0,t*),
证明了该方程存在爆破解, 并对爆破时间进行了估计.2016年, Xia等[8]研究了半线性抛物方程
ut=Δum+f(t)g(u), (x,t)∈Ω×(0,T),
其边界条件为u(x,t)=0,(x,t)∈∂Ω×(0,T),证明了解的全局存在性, 解在有限时间内爆破, 并给出了爆破时间的上下界估计. 同年,Xia等[9]研究了方程组的相似情形. 其它的相关工作还可参见文献[10-13].
另一方面,在文献[5]中, Du给出了拟线性退化方程(组)爆破解的处理方法. 受此启发, 我们利用该文中的方法对问题(1)进行研究. 我们将首先建立(1)的局部存在性和比较原理,在此基础上给出(1)的整体存在和爆破的条件. 我们的主要结果如下.

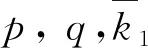
定理1.3假设存在正常数p,q及ξ>0使得f1(ξ)≥ξp,f2(ξ)≥ξq成立, 且k1=min{infk1(t),infk2(t)}>0. 若pq>mn, 则问题(1)的每个古典解对大的初值u0(x),v0(x)在有限时间内爆破.
2 比较原理
在本节中我们证明定理1.1.固定ε>0并定义u0,v0为
u0=u(x,0)+ε,v0=v(x,0)+ε
(2)
对n=1,2,3,…, 归纳定义un,vn为下述问题的解:
(3)
容易看出,un≤un-1,vn≤vn-1(n=1,2,…). 对n=1, 该不等式是我们的假设. 换言之, 我们假设u0≥u1,v0≥v1. 设该不等式对n-1成立, 即
un-1≤un-2,vn-1≤vn-2.
那么
un-1,t-Δun-1(x)m-k1(t)f1(vn-1)≥
un-1,t-Δun-1(x)m-k1(t)f1(vn-2)=0,
vn-1,t-Δvn-1(x)n-k2(t)f2(un-1)≥
vn-1,t-Δvn-1(x)n-k2(t)f2(un-2)=0,
un-1(x,0)≥un(x,0),vn-1(x,0)≥vn(x,0).
因而(un-1,vn-1)是问题(3)的一个上解,从而
un≤un-1,vn≤vn-1.
定义
当IΩ(u,v,χ)=JΩ(u,v,χ)=0时,我们称(u,v)是(1)的弱解.
设η满足
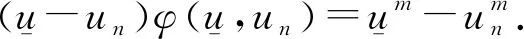
且
因此
同理,
这意味着
3 整体解的存在性
为了后面证明方便, 我们首先不加证明地引入下边两个引理.记
引理3.1若pq
引理3.2若pq>mn, 则存在正常数l1,l2使得AL<(0,0)T且A(cL)<(0,0)T对所有c>0成立.

设φ(x)是

(4)
(5)
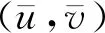
(1+φ(x))ml1-2|φ(x)|2+
(1+φ(x))ml1-1Δφ(x)}≥
-ml1Kml1(1+φ(x))ml1-1Δφ(x)=
ml1Kml1(1+φ(x))ml1-1≥
ml1Kml1(1+C)ml1-1
(6)
(7)
类似可得
nl2Knl2(1+C)nl2-1
(8)
及
(9)
其中
(10)
若pq
(K(φ(x)+1))l1≥u0(x),
(K(φ(x)+1))l2≥v0(x)
(11)
4 解的有限时间爆破
在定理1.3的证明中,我们采用Du在文献[5]中的证明思想.
首先,由比较原理, 我们构造问题(1)在Ω的某个子区域内的上解, 其中u,v>0.
设ψ(x)是一个平凡的非负连续函数且在∂Ω上为零. 不失一般性, 我们假定0∈Ω且ψ(0)>0. 接下来, 我们构造问题(1)的一个爆破上解. 记
(12)
其中
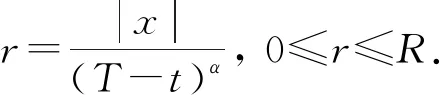

对充分小的T,记

B(0,R(T-t)α)⊂B(0,RTα)⊂Ω
(13)

(14)
且
(15)
其中T>0充分小.

(16)
(17)
从而
(18)
(19)

(20)
(21)
如果pq>mn, 由引理3.2知存在两个正常数l1,l2, 使得
ml1-pl2<-1,nl2-ql1<-1,
(m-1)l1>1, (n-1)l2>1.
这样,我们得到
pl2>ml1+1>l1+1,ql1>nl2+1>l2+1
pl2>ml1+1>l1+1,ql1>nl2+1>l2+1.
因此, (13)式对充分小的α>0和T>0成立. 应用式(18)~(21)得
(22)