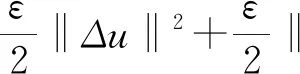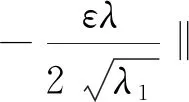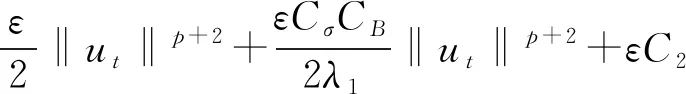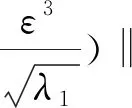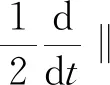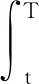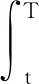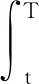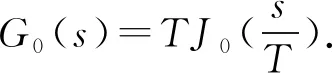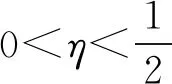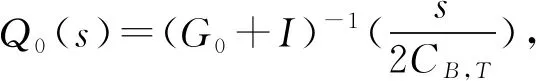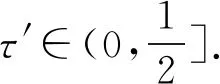带非局部弱阻尼项的耦合吊桥方程的全局吸引子

王露露, 马巧珍

(西北师范大学数学与统计学院, 兰州 730070)

1 引言

本文考虑带有非局部弱阻尼项的耦合吊桥方程

(1)

全局吸引子的存在性,其中‖ut‖put, ‖vt‖pvt为非局部弱阻尼项,p≥0,k2是弹性系数, 外力项hB(x),hS(x)∈L2(Ω), 函数(u-v)+=max{(u-v),0}. 为简便起见记Ω=[0,L],Δ2u=uxxxx, -Δv=-vxx.

近年来, 关于吊桥方程全局吸引子的研究已取得了一系列重要成果[1-17],2005年, 文献[2]首次获得了耦合吊桥方程弱解的全局吸引子. 之后, 文献[3] 证得了吊桥方程的强解和强全局吸引子的存在性. 此外， Park和Kang在文献[4] 中研究了带有非线性阻尼的吊桥方程全局吸引子的存在性，文献[8] 获得了非自治耦合吊桥方程一致吸引子的存在性，文献[9]借助收缩函数的方法得到了具有时滞的非自治吊桥方程拉回吸引子的存在性.

最近, 文献[10] 通过能量重建的方法得到了带有非局部弱阻尼项的可扩展梁方程在次临界情况下全局吸引子的存在性. 本文借助文献[10] 提出的方法研究了带有非局部弱阻尼的耦合吊桥方程 (1) 解的长时间动力学行为. 由于方程组的耦合体现在半线性项(u-v)+, 所以文献[10] 中的能量重建方法在我们的问题上不会产生新的困难.

本文结构如下.第2节给出必要的预备知识并借助单调算子理论获得了解的适定性.第3节获得了解半群{S(t)}t≥0的耗散性, 证明了问题 (1) 全局吸引子的存在性. 本文出现的C或Ci均表示正常数, 且后续出现的每一处C并不完全相同.

2 预备知识

H=V2×V0×V1×V0,

并赋予范数

‖(u,ut,v,vt)‖H=

根据 Poincaré 不等式可得

‖Δu‖2≥λ1‖u‖2, ∀u∈V2,

(2)

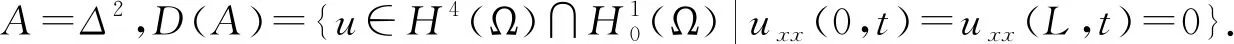
此外, 设非线性项fB∈C1(R),fS∈C1(R)且满足以下假设条件：

(3)

(4)

根据 (4) 式和中值定理可知, 存在两个正常数K1和K2, 使得对任意u,v∈R有

|fB(u)-fB(v)|≤K1(1+|u|ρ+|v|ρ)|u-v|

(5)

|fS(u)-fS(v)|≤K2(1+|u|ρ+|v|ρ)|u-v|

(6)

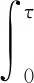
(7)

(8)

引理2.1[12]设X是一可分的Banach空间,Lp(a,b;X)表示Bochner可测函数f:[a,b]→X构成的空间, 1≤p≤∞使得‖f(·)‖X∈Lp(a,b). 则每一个Lp(a,b;X)是Banach空间, 且具有范数

‖f‖L∞(a,b;X)=esssup{‖f(t)‖X:t∈[a,b]}.

我们用C(a,b;X)表示取值于X中的强连续函数空间,

W1,p(a,b;X)=

{f∈C(a,b;X):f′∈Lp(a,b;X)},

其中f′(t)表示f(t)关于t的分布导数. 注意到空间W1,1(a,b;X)与从[a,b]到X上的绝对连续函数集合相一致.

定义2.2[10,12]设函数u(t),v(t)∈C([0,T];V2×V1), 初值u(0)=u0,ut(0)=u1,v(0)=v0,vt(0)=v1.它被称为是

(S) 问题 (1) 在区间[0,T]上的强解, 如果

(i) ∀0

(G) 问题 (1) 在区间[0,T]上的广义解, 如果存在问题 (1) 的强解子序列{un(t)},{vn(t)},其初值为(u0n,u1n,v0n,v1n), 使得

(Dut(σ),ω)+((hB-k2(u-v)+-

fB(u)),ω))dσ

(9)

(Dvt(σ),ν)+((hS+k2(u-v)+-

fS(v)),ν))dσ

(10)

定理2.4[10]设u,v∈H,H是一个Hilbert空间, 其内积和范数分别为(·,·)和‖·‖H. 那么存在依赖于γ的正常数Cγ, 使得

推论2.5[10]令D(μt)=‖μt‖pμt.由定理2.4可得

(D(μt)-D(υt),μt-υt)≥Cp‖μt-υt‖p+2,

p≥0,μt,υt∈V0

(11)

从而阻尼算子D是强单调的.

定理2.6设任意的T>0.在假设 (3)，(4) 的条件下, 以下结论成立:

(ut,utt,vt,vtt)∈L∞([0,T];V2×V0×V1×V0),

(ut,vt)∈Cr([0,T];V2×V1),

(utt,vtt)∈Cr([0,T];V0×V0),

Au(t)+Dut(t)∈Cr([0,T];V0′),

其中Cr表示右连续函数的空间, 且方程的解满足能量关系

(12)

其中

(13)

(14)

(ii) 对任意(u0,u1,v0,v1)∈V2×V0×V1×V0, 存在唯一的广义解, 使得

(u,ut,v,vt)∈C([0,T];V2×V0×V1×V0)

(15)

定理2.6的证明类似于文献[10]中定理2.3的证明, 故我们只给出上面的结论.

推论2.7问题 (1) 在空间H上生成了一个动力系统(H,S(t)), 其中

S(t)(u0,u1,v0,v1)=(u(t),ut(t),v(t),

vt(t))，

而(u(t),v(t))是初值为(u0,u1,v0,v1)的方程 (1) 的解.

为了证明主要结论, 我们还需要下面的一些定义和结果.

其中dX{A,B}=supx∈AdistX(x,B)是Hausdorff 半距离.

定义2.9[12]一个有界闭集A⊂X被称为是系统(X,S(t))的全局吸引子, 如果

(i)A是不变集, 即对任意t≥0有S(t)A=A;

(i) ∀s>0,r(s)

(iii) 下列不等式成立:

d(S(T)y1,S(T)y2)≤r(d(y1,y2)+

(16)

其中{S(τ)yi}由空间C(0,T;X)中的函数yi(τ)=S(τ)yi,i=1,2给出. 则(X,S(t))是渐近光滑的动力系统.

定理2.11[12]设(X,S(t))是一个完备度量空间X上的耗散动力系统.则(X,S(t))拥有一个紧的全局吸引子当且仅当它是渐近光滑的.

3 全局吸引子

定理3.1假设条件(3)，(4)成立，且由问题(1)生成的动力系统(H,S(t))在空间H是耗散的.则存在R>0, 对任意有界集合B⊂H,t0=t0(B)>0, 使得对所有的y∈B, 当t≥t0时有

‖S(t)y‖H=‖(u(t),ut(t),v(t),

vt(t))‖H≤R.

证明 分别用ut+εu和vt+εv与 (1) 的两个方程在L2(Ω)上做内积, 计算相加后可得

ε‖vt‖2+ε‖v‖2+εk2‖(u-v)+‖2+

(‖ut‖put,ut+εu)+(‖vt‖pvt,vt+εv)+

(17)

结合(2)和(7)式得

(18)

根据Hölder不等式、Young不等式和 (2) 式有

(19)

结合 (13)(14) 式和(18)(19)式有

E(t)≥c0E0(t)-C0, 0

(20)

令W(t)=E(t)+(ut，εu)+(vt，εv).根据Hölder不等式和Young不等式有

(21)

结合(20)(21)式, 存在ε0>0, 使得当0<ε<ε0时

W(t)≥c1E0(t)-C1, 0

(22)

将(17)式写为

(23)

其中

Y(t)=(‖ut‖put,ut+εu)+

ε2(ut,u)-ε2(vt,v)

(24)

结合 (2) 式和(8) 式可得

(25)

(26)

由Young不等式知,存在c2,c3>0使得

(ut,ut)=‖ut‖2≤c2+c3‖ut‖p+2

(27)

由 (12) 和 (20) 式, 存在CB>0使得

E0(t)≤C(1+E(t))≤C(1+E(0))≤CB

(28)

根据Cauchy不等式、Young不等式及 (2)(28) 式有

|(‖ut‖put,εu)|≤

(29)

同理，由(28)式可得

(30)

结合 (29),(30)式得

|(‖ut‖put,ut+εu)|≥

(31)

|(‖vt‖pvt,vt+εv)|≥

(32)

由 (24) ～ (27) 式及 (31)，(32)式可得

取充分小的ε>0, 使得

则有Y(t)≥-εC4.将其代入到 (23) 式可得

(33)

根据Gronwall不等式, 我们有

W(t)≤W(0)e-εt+C4(1-e-εt)

(34)

(35)

显然, 定理3.1意味着集合B0={(u(t),ut(t),v(t),vt(t))∈H:‖(u(t),ut(t),v(t),vt(t))‖H≤R}是与问题 (1) 相关的解半群{S(t)}t≥0的有界吸收集.

定理3.2假设条件 (3),(4) 成立.则存在T0>0及与T无关的常数C>0, 使得对问题 (1) 的任意两个强解(u1,v1),(u2,v2), 当T≥T0时成立下面的关系式:

(36)

其中

ξ(t)=u1(t)-u2(t),ζ(t)=v1(t)-v2(t),

且

‖ζt‖2+‖ζ‖2),

D(t,ξt)=‖u1t‖pu1t-‖u2t‖pu2t,

D(t,ζt)=‖v1t‖pv1t-‖v2t‖pv2t.

证明 注意到ξ(t)=u1(t)-u2(t),ζ(t)=v1(t)-v2(t)满足如下两式:

ξtt+ξxxxx+D(t,ξt)+k2(u1-v1)+-

k2(u2-v2)++fB(u1)-fB(u2)=0

(37)

ζtt-ζxx+D(t,ζt)-k2(u1-v1)++

k2(u2-v2)++fS(v1)-fS(v2)=0

(38)

将 (37), (38) 式分别与ξt,ζt在L2(Ω)上做内积, 计算相加后得

(k2(u1-v1)+-k2(u2-v2)+,ξt)+

k2(u2-v2)+,ζt)+(fS(v1)-fS(v2),ζt)=0

(39)

则

-(k2(u1-v1)+-k2(u2-v2)+,ξt)+

(k2(u1-v1)+-k2(u2-v2)+,ζt)-(fB(u1)-

fB(u2),ξt)-(fS(v1)-fS(v2),ζt)

(40)

对(40) 式在[t,T]上积分可得

k2(u2-v2)+,ξt)dτ+

(41)

将(37), (38) 式分别与ξ,ζ在L2(Ω)上做内积, 计算相加后得

‖ζt‖2+‖ζ‖2+(D(t,ξt),ξ)+

(D(t,ζt),ζ)=-(k2(u1-v1)+-

k2(u2-v2)+,ξ)+(k2(u1-v1)+-

k2(u2-v2)+,ζ)-(fB(u1)-

fB(u2),ξ)-(fS(v1)-fS(v2),ζ)

(42)

对 (42) 式在[0,T]上积分可得

结合 (2) 式和连续嵌入定理有

(43)

因此,我们有

(44)

在 (41) 式中令t=0有

(45)

此外, 因算子D是单调的, 将 (41) 式在[0,T]上积分可得

(46)

由插值不等式有

(47)

根据|(u1-v1)+-(u2-v2)+|≤L|(u1-v1)-(u2-v2)| (L>0是一恰当的常数), 及‖(u,ut,v,vt)‖H≤R. 结合Young不等式和 (2)(47) 式有

|(k2(u1-v1)+-k2(u2-v2)+,ξ)|≤

Lk2‖(u1-v1)-(u2-v2)||·‖ξ‖=

Lk2‖ξ-ζ‖·‖ξ‖≤C(R)‖ξ‖2

(48)

同理可得

|(k2(u1-v1)+-k2(u2-v2)+,ζ)|≤

C(R)‖ζ‖2

(49)

|(k2(u1-v1)+-k2(u2-v2)+,ξt)|≤

C(R)‖ξ‖·‖ξt‖

(50)

|(k2(u1-v1)+-k2(u2-v2)+,ζt)|≤

C(R)‖ζ‖·‖ζt‖

(51)

结合 (44) ～ (51) 式即得(36) 式.证毕.

接下来我们将证明问题 (1) 所对应的解半群{S(t)}t≥0是渐近光滑的.

命题3.3假设条件 (3)(4) 成立.则问题 (1) 生成的动力系统(H,S(t))在空间H上是渐近光滑的.

证明 由定理 3.1 可知, 集合B0是与问题 (1) 相关的解半群{S(t)}t≥0的有界吸收集. 根据定义，我们知道存在t0≥0, 使得对所有的t≥t0有S(t)B0⊂B0.令B=∪t≥t0S(t)B0. 显然B是系统(H,S(t))的有界正不变集. 于是，对任意有界集合B′, 当t≥t(B′)时有S(t)B′⊂B0，即对所有的t≥t0+t(B′)有S(t)B′⊂B. 因此，B也是有界吸收集.

设(u1,v1)和(u2,v2)是问题 (1) 在不变集B上关于两个不同初值的强解, 即对任意y0,y1∈B有

(u1(t),u1t(t),v1(t),v1t(t))=S(t)y0,

(u2(t),u2t(t),v2(t),v2t(t))=S(t)y1

(52)

由于(16)式的所有项对于能量范数‖·‖E所给出的度量d都是连续的, 其也满足定理2.10中的条件. 设T>0. 由于B是有界正不变集, 由能量等式 (12) 式有

(53)

第一步,能量重建.由 (36) 式, 令

进一步, 根据ΦT的定义有

(54)

(55)

(56)

‖fB(u1)-fB(u2)‖2=

(57)

其中0<θ<1. 同理可得

(58)

因此, 由(57),(58)式我们有

(59)

(60)

结合 (54) ～ (60) 式，我们有

(61)

J0((‖u+v‖p(u+v)-‖u‖pu,v))≥

J0(Cp‖v‖p+2)=‖v‖2,u,v∈V2×V1

(62)

由Jensen不等式可得

(63)

(64)

‖u2t‖pu2t)2dx)1/2≤

C‖ξ‖(‖u1t‖2p‖u1t‖2+

‖u2t‖2p‖u2t‖2)1/2≤CB‖ξ‖≤

(65)

同理可得

(66)

结合定理3.2和 (61) ～ (66) 式, 对于任意κ>0有

(67)

第二步,处理阻尼.对于 (67) 式, 令δ=min{ω,η}.则

(68)

(69)

根据 (45)(50)(51)(57) 式和紧嵌入定理有

Em(0)-Em(T)-

(70)

则由(69) 式可得

Em(T)+2Q0(Em(T))≤Em(0)-Em(T)+

(71)

CR‖ξ(t)‖1-η1, 0<η1<1

(72)

CR‖ζ(t)‖1-η2, 0<η2<1

(73)

则对于任意的τ∈(0,1] 有

Em(T)+2Q0(Em(T))≤Em(0)+

(74)

于是

(75)

(76)

(77)

我们有

‖S(T)y1-S(T)y2‖H≤r(‖y1-y2‖+

(78)

显然, 函数r满足定理2.10的全部条件.

最后, 由定理3.1和命题3.3即得我们的主要结论:

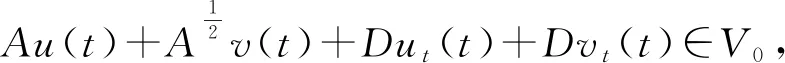
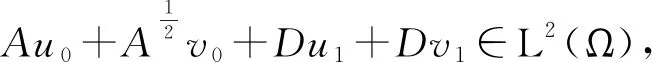
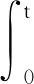
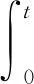
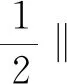
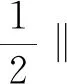
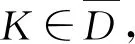
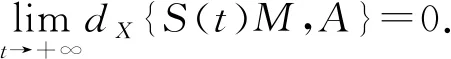
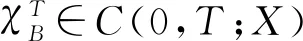
定理3.4假设条件 (3)(4) 成立. 则由问题 (1) 生成的动力系统(H,S(t))在空间H上拥有紧的全局吸引子.