基于离散元的膏体搅拌影响因素分析

李 雪 李翠平 颜丙恒 侯贺子

（1.北京科技大学土木与资源工程学院，北京100083；2.金属矿山高效开采与安全教育部重点实验室，北京100083）

开发矿产资源会产生大量尾矿，尾矿中重金属离子会污染地表水与地下水，长时间堆积的尾矿可能引发泥石流等灾害，对环境造成严重危害。膏体充填技术能够解决尾矿堆积带来的问题，近年来备受关注并得到快速发展。膏体充填技术既能解决使用骨料带来的材料成本问题，又能使尾砂得到合理处置，实现环境、资源和安全等多方面协调发展［1-3］，从而使得膏体充填工艺成为建设“绿色矿山”的有效方法。膏体充填工艺将经过浓密环节的高浓度尾砂料浆、骨料与胶凝材料等物料在地面经过搅拌等工序，由泵送或自流输送到井下充填采空区。搅拌过程是使膏体在充入采场前保持稳定状态的重要环节［4］，膏体的组成成分能否在搅拌过程中有效分散影响着膏体的流动性能，也影响着充填工艺能否顺利进行［5-7］。膏体搅拌技术与设备主要借鉴于混凝土行业，但是混凝土与膏体的物化性质与粒级组成差别较大，导致膏体的流动特性与混凝土有所不同［8-9］，如何发展搅拌技术，进而生产出满足充填工艺需求的膏体是亟待解决的问题。然而国内外膏体充填技术的研究主要专注于浓密、管道输送以及充填等环节［10-11］，对搅拌环节的研究局限于宏观尺度［12-13］，关于料浆在搅拌过程中的流动行为与工艺参数对料浆微细观结构演变的影响缺乏深入的分析［14］，因此研究搅拌过程中膏体的流动行为具有十分重要的理论意义和工程参考价值。

膏体充填工程中屈服应力可用于判断料浆是否发生流动，坍落度试验是表征膏体屈服应力值的有效手段，被广泛应用于混凝土行业和矿业领域［15-16］。混凝土行业通常采用标准ASTM锥型坍落筒测量屈服应力，然而使用其测量膏体屈服应力存在一定的误差［17］。有研究表明，采用小型圆柱坍落筒测得的数据更可靠［18］，且在低应力条件下使用圆柱型坍落筒较为合适［19］，小型圆柱坍落筒更适用于研究膏体的流动性能。

物料在搅拌环节中运动形式更为复杂，不同尺度的物料在搅拌机内发生剧烈碰撞［20］，为保证膏体中不同物料混合均匀，对搅拌设备也有更高的要求。两段连续搅拌设备中二段搅拌通常使用双轴螺旋搅拌输送机，主要起到输送物料的作用，但搅拌能力较差。优化二段搅拌设备可进一步提高搅拌效率，为制备出不离析、不沉淀、不脱水的膏体，有必要针对双轴螺旋输送机的搅拌机理展开探究［21］。本研究通过开展试验与数值模拟，建立符合全尾砂膏体流变性质的离散元模型，同时构建双轴螺旋输送机数值模型研究料浆在输送机中的流动特性，分析不同工艺参数对膏体混合效果的影响。

1 试验原理

1.1 坍落度试验力学分析

坍落筒可直观表现膏体的流动性能［22-23］。图1为坍落度试验示意图，坍落筒内膏体视作整体，以坍落筒上端圆口中心线作为Z轴，水平线作为Y轴建立直角坐标系，假设膏体具有弹性且不可压缩，提起圆柱坍落筒时膏体不会发生变形。为使模型对于不同材料以及坍落筒都有普适性，需要将模型中的变量进行无量纲化处理。

坍落筒提起后膏体发生流动，料浆受到自重与黏性力作用，位于未屈服段h0'以下的料浆受到的应力大于屈服应力，这部分料浆流动直至其所受应力小于屈服应力；位于未屈服段以上的料浆，其受到的应力小于屈服应力，该部分料浆不会发生流动。由无量纲坍落度及无量纲未屈服段高度可知，屈服应力与坍落度之间的关系可表述为：

式中，ρ为料浆密度，kg/m3；h为坍落筒高度，m；s为坍落度，m；s'为无量纲坍落度，s'=s/h；h0为未屈服段高度，m；h0'为无量纲的未屈服段高度，h0'=h0/h；h1为屈服段高度，m；τy为屈服应力，Pa；τy'为无量纲屈服应力，τy'=τy/(ρgh)。

1.2 离散单元法

离散单元法兴起于20世纪70年代，最早用于研究不连续岩体的变形，CUNDALL和STRACK将其应用于不连续介质力学［24］。离散单元法针对颗粒运动及相互作用进行模拟，使用时间步长迭代法求解颗粒运动方程，从而得出不连续体的整体运动形态。该方法既可跟踪颗粒在流动过程中的运动，也可模拟颗粒与颗粒、颗粒与边壁发生的碰撞。恰当地构建离散元模型并将其应用于模拟坍落度试验，再现膏体流变行为，展现料浆微观结构，并反映膏体颗粒间相互作用规律［25］，是一种较为有效的模拟方法。

本研究引入 Hertz-Mindlin with JKR［26］模型模拟膏体坍落度试验。该模型以软球模型为基础，颗粒间法向分力简化为弹簧与滑动器，切向分力简化为弹簧、阻尼器和滑动器，引入弹性系数和阻尼系数等参量。颗粒的法向接触力Fn可进行如下计算：

式中，E*为接触颗粒的当量杨氏模量，Pa；Ei、Ej为接触颗粒i与j的杨氏模量，Pa；μi、μj为颗粒i与j的泊松比；R*为接触颗粒i与j的当量直径，m；Ri、Rj为颗粒i与j的直径，m；δn为接触颗粒i与j的法向重叠量，m。

法向阻尼力的计算公式为

切向接触力Ft以及切向阻尼力可分别进行如下计算

式中，St为颗粒的切向刚度，N/m；δt为接触颗粒的切向重叠量，m；G*为等效剪切模量，Pa；为相对切向速度，m/s。

滚动摩擦力可由力矩进行表示：

式中，μr为滚动摩擦系数；Ri为接触点到颗粒质心的距离，m；ωi为颗粒i在接触点处的单位角速度，rad/s。

在相同条件下，由试验或模拟得到的数据会有差异，故本研究引入变异系数Cv判断数据离散程度，其公式为

式中，σ与μ'为数据的标准差与平均值，变异系数反映了数据的离散程度，取值越大，表明试验数据越离散，试验可靠性越差。

2 试验材料及设备

2.1 试验材料

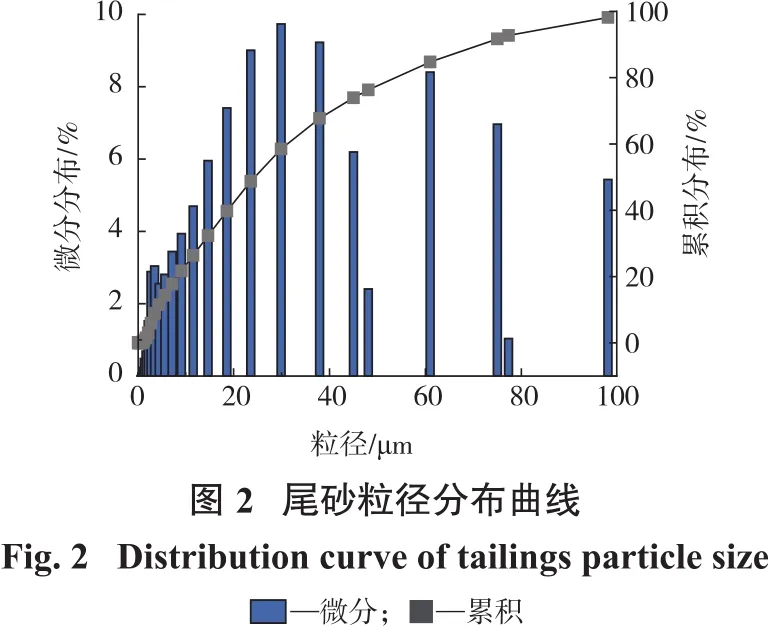
本研究试验材料来自某铁矿尾砂，粒级组成如图2所示，密度为2.696 g/m3，中值粒径为24.306 μm，体积平均粒径为31.567 μm，表面积平均粒径为10.697 μm，尾砂中粒径小于20 μm的颗粒累计质量分数为39.76%，细颗粒（-20 μm）含量偏高。

2.2 试验设备

坍落度试验设置膏体固体质量分数为72%，为探究不同尺寸及材质坍落筒的试验效果，共设计了3种不同材质及尺寸坍落筒，基本参数如表1所示。

为检验坍落度试验结果的准确性，使用流变仪开展CSR试验。流变仪采用美国博勒飞（Brookfield）RST型流变仪，该型号流变仪在试验中对膏体的网络结构扰动较小。试验数据导入Rheo3000软件进行数据分析。

2.3 膏体离散元模型

使用离散元分析软件模拟坍落度试验与膏体搅拌过程，选择Hertz-Mindlin with JKR接触方法，颗粒本征参数及接触参数如表2所示。模拟中固体质量分数与坍落度试验保持一致，颗粒形态设置为球形，坍落筒提升速度设定为1 m/s。

3 坍落度试验及离散元模型校核

3.1 坍落度试验

坍落筒试验数据如图3所示，图中显示平均屈服应力为B＞C＞A，CSR试验测得该固体质量分数下膏体静态屈服应力为86.65 Pa，坍落筒A更为接近，B和C偏差较大；比较3种坍落筒变异系数有C＞B＞A，坍落筒A结果比其他两组数据更小，该组数据离散程度更小，使用坍落筒A能够保证试验具有较好的可靠性。

比较A组与C组的变异系数可知，坍落筒材质对试验结果影响较大，是因为在静置状态下，坍落筒表面粗糙度大，导致膏体密实度差，膏体无法将坍落筒填满，且在坍落筒提升过程中，膏体受到的摩擦力也很大，致使膏体坍落形态发生很大变化。不锈钢材质坍落筒表面较PVC材质坍落筒表面更粗糙，故选用PVC材质坍落筒能够提高试验的可靠性。

比较B组与C组数据发现，坍落筒高径比对试验结果也有一定的影响。坍落筒高径比越大，致使变异系数越大，数据离散程度更大。这与力学模型有关，坍落筒高径比增加，填充坍落筒所需的膏体增加，颗粒间相互作用更加复杂，而力学模型忽视坍落筒高度，不同高径比的坍落度试验结果由此产生差异。人为操作因素也会影响试验效果，膏体填充过程中仪器轻微倾斜及内部残余气泡、测量时读数误差等也会对试验结果产生影响，造成试验结果计算得出的无量纲屈服应力出现偏差。

综上分析，坍落筒材质以及高径比对试验结果影响都很大，同时无法排除人为因素的干扰。通过比较不同坍落筒的试验数据得到直径为50 mm以及高度为120 mm的PVC材质坍落筒的试验结果更接近流变仪试验数据，测得屈服应力为84.55 Pa，变异系数为0.092，数据离散度较低。

3.2 膏体离散元模型校核

坍落度试验模拟过程如图4所示，模拟前预设底板和圆柱型坍落筒，颗粒工厂设置在坍落筒中，0～1 s生成颗粒；模拟时坍落筒静置1.5 s，再匀速向上提升坍落筒，当膏体坍落速度及扩展速度均小于10-4m/s时，认为膏体不再流动，坍落度试验模拟结束。

坍落度试验与坍落度模拟最终坍落形态如表3所示。试验所得坍落度、扩展度分别为80.875 mm、135.28 mm，模拟所得坍落度、扩展度分别为88.086 mm、140.360 mm，误差均小于10%，仿真结果与试验吻合，膏体离散元模型接触参数的正确性得到了验证。

4 膏体搅拌机模型构建及模拟

4.1 双轴螺旋输送机模型构建

通过第3节的试验与模拟，分析了膏体在剪切作用下的流变特性，能够为接下来探究料浆在搅拌环节中的运移规律做铺垫。搅拌环节离不开搅拌设备，本研究针对双轴螺旋输送机的搅拌机理展开探究。图5为输送机几何模型，模型还原了搅拌槽与搅拌轴，其中搅拌轴由搅拌杆、支撑臂、外圈大叶片与内圈小叶片构成，输送机最大容积为5 m3，搅拌槽长4.8 m，搅拌轴长为6 m。

利用相似性原理将几何尺寸缩小为原型的1/10，设定入料槽为颗粒工厂，颗粒在入料槽中生成，生成两组颗粒，两组颗粒参数保持一致。颗粒工厂生成颗粒速度为2 000个/s，颗粒产生位置随机，随后颗粒在自重及其他颗粒作用下运动至输送机中。输送机中搅拌轴从0 s开始做旋转运动，两侧搅拌轴旋转方向相反，膏体颗粒在搅拌轴和其他颗粒等多重作用下发生运动。

为研究不同工艺参数对膏体均质性的影响，添加了P1与P2两种颗粒群，设置7组初始条件不同的模型，其工艺参数如表4所示。通过对比组A、组B、组C和组D来分析充盈率对膏体混合度的影响，组E、组F、组C和组G中搅拌转速不同，目的是探究搅拌转速对膏体均质性的影响。

4.2 充盈率对膏体均质性的影响

搅拌时间20 s时，不同充盈率条件下的颗粒角速度分布如图6所示。图中显示角速度较高的颗粒密度随充盈率增大逐渐增加，在充盈率为0.6时角速度较高的颗粒密度达到最大，而后随充盈率增加而减少。这说明更多料浆进入输送机后，颗粒无法在叶片带动下获得足够的角速度，颗粒间运动也由此受到限制，充盈率过大导致颗粒间运动明显减少，料浆的混合程度无法保证。

不同充盈率条件下颗粒平均角速度变化特征如图7所示。图7（a）显示颗粒在落入搅拌槽后角速度会大幅度增加，而后在其他颗粒作用下角速度减少至固定区间内，颗粒角速度在该区间内波动；充盈率为0.4时颗粒角速度数据波动最大，随着充盈率增加，波动范围依次降低，说明在充盈率较低的情况下，颗粒间运动更剧烈。图（b）显示随着充盈率增加，颗粒平均角速度呈现减少趋势，说明较少的料浆进入输送机后，在叶片推动下更容易获得更大的角速度，颗粒间碰撞更加剧烈，膏体均质性也由此受到影响。

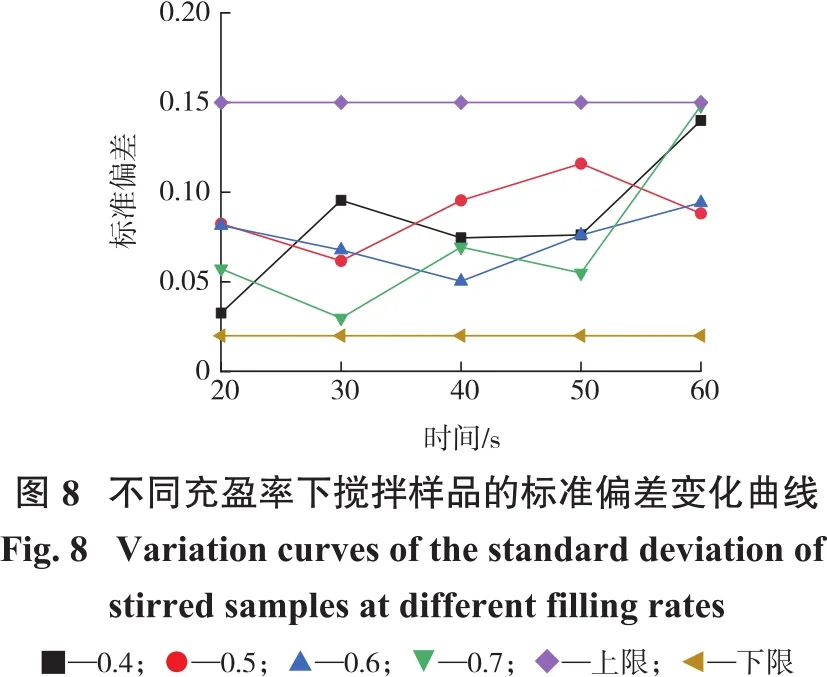
搅拌时间为20～60 s时，每隔10 s在搅拌槽中相同位置取样，以标准偏差作为指标来衡量样品的混合程度，样品中两组物料颗粒数相同视为膏体混合均匀。样品标准偏差变化如图8所示，由该图可知：搅拌样品标准偏差一般在0.02～0.15范围内波动。搅拌时间为20 s时，充盈率为0.4与0.7的样品标准偏差明显小于充盈率为0.5和0.6的样品数据。搅拌时间为30～60 s时，充盈率为0.4和0.7样品的标准偏差持续增加，且增加幅度较大，搅拌后期样品标准偏差要大于前期数据；充盈率为0.5和0.6模型表现较好，在30～60 s区间内标准偏差会小幅度增加而后下降，60 s时二者的标准偏差要小于充盈率为0.4和0.7样品的数据，说明充盈率为0.5和0.6的模型在搅拌后期料浆混合效果良好。

充盈率对出料样品的混合程度有一定的影响，搅拌时间为65 s时，在输送机中靠近出料槽部分取相同质量样品，不同充盈率条件下出料样品数据的变化特征如图9所示。由图9可知：标准偏差在0.10～0.18区间内波动，随着充盈率增加，样品的标准偏差呈现先上升、后下降、再上升的趋势，充盈率为0.6时达到最小值0.107。相比于充盈率为0.6的模型，充盈率为0.4的模型搅拌效果较差，说明更少的料浆进入输送机中，虽然颗粒间碰撞更加剧烈，但出料样品的混合效果并不理想。

综合比较搅拌样品与出料样品的标准偏差变化特征可知，充盈率为0.6的模型数据表现良好，料浆在搅拌过程中能够得到充分分散，故应存在最佳充盈率，取值范围为0.5～0.7。

4.3 搅拌转速对膏体均质性的影响

搅拌时间20 s时输送机同一位置颗粒角速度分布如图10所示。由图10可知：转速10 rpm时角速度较低的颗粒密度最大，随着搅拌速度增大，角速度较低的颗粒密度逐渐降低，角速度较高的颗粒密度逐渐增加，搅拌转速为40 rpm时角速度较高的颗粒密度达到最大。以上说明叶片转动可促进颗粒发生循环流动，叶片转速增大，输送机赋予膏体颗粒的能量增多，颗粒间相对运动越剧烈，颗粒簇能够被快速打散，较大的搅拌速度有助于膏体均质状态的形成。

图11为不同搅拌转速下颗粒角速度的变化趋势。图11（a）显示不同转速模型颗粒平均角速度都会在10 s内达到稳定值，其后在该值附近浮动。图（b）显示平均角速度与搅拌转速呈正相关关系，随着转速增加，膏体平均角速度增大，但增加幅度逐步降低，搅拌转速增加可促进膏体颗粒间发生剧烈的相对运动，但转速增加到一定程度后对颗粒运动的促进作用逐渐降低，适宜的搅拌转速有助于颗粒实现快速混合。

在搅拌时间20～60 s范围内，每隔10 s在搅拌槽中相同位置取样，搅拌样品数据如图12所示，样品标准偏差在0.04～0.15范围内波动。搅拌时间为20 s时，标准偏差随着搅拌转速增加而降低，在转速40 rpm时达到最小值0.055。随着搅拌时间增加，不同搅拌转速条件下搅拌样品的标准偏差变化不同。搅拌时间为60 s时，搅拌转速为20 rpm以及40 rpm的样品标准偏差大于搅拌时间10 s时数据，且转速为40 rpm样品标准偏差在取样时间区间内波动极大；搅拌转速10 rpm和30 rpm的样品在搅拌时间60 s时的标准偏差小于10 s数据，转速为10 rpm和30 rpm时膏体混合程度优于转速20 rpm与40 rpm的模型，故搅拌转速为10 rpm以及30 rpm搅拌效果更好。

充盈率对出料样品混合程度有一定的影响。搅拌时间为65 s时，在输送机中靠近出料槽部分取相同质量样品，出料样品数据如图13所示。由该图分析可知：4份样品标准偏差均在0.16以下，出料样品标准偏差随着搅拌转速增大而增加，搅拌转速为40 rpm时，样品标准偏差达到最大值0.151，转速由30 rpm增加至40 rpm后，标准偏差增加幅度达到最大。这说明搅拌转速能够促进颗粒间相对运动，搅拌转速过大则无法保证膏体的混合程度。

综合分析搅拌样品与出料样品数据可知，搅拌转速为10 rpm和30 rpm时膏体料浆混合程度较好，考虑到需要保证膏体的出料效率，故认为30 rpm为输送机的最佳搅拌转速。

5 结论

以试验与数值模拟作为研究手段，由坍落度试验测得数据表征膏体的流变特性，将膏体作为具有强黏性的湿颗粒群，采用离散单元法进行仿真，能够较好地体现膏体的流变特性，分析了充盈率与搅拌转速对膏体搅拌均质性的影响，得到如下结论：

（1）通过比较不同高径比与材质坍落筒的试验结果，认为高径比与数据离散度呈正相关关系，高径比越大，屈服应力值越集中；坍落筒材质会对试验结果产生影响，不锈钢材质坍落筒测得的数据较PVC材质坍落筒的数据更分散，直径为50 mm、高度为120 mm的PVC材质坍落筒的试验效果较为理想，测得屈服应力值为84.55 Pa。采用离散元分析软件模拟上述试验，通过比较不同工艺参数条件下膏体的均质性变化情况，发现充盈率影响膏体搅拌效果，搅拌前期混合程度较好的样品随着搅拌时间增加，标准偏差逐渐增大，充盈率为0.5以及0.6的膏体表现出较好的均质性；出料样品数据证明充盈率为0.6的模型混合效果较好，故充盈率最佳取值范围为0.5～0.7。搅拌转速能够促进颗粒间发生剧烈运动，随着搅拌时间增加，搅拌转速为10 rpm和30 rpm的模型中料浆搅拌效果要好于转速为20 rpm与40 rpm的模型；出料样品数据显示搅拌转速增加导致颗粒混合程度降低，考虑到出料效率，30 rpm为输送机最佳搅拌转速。

（2）采用离散单元法构建的膏体颗粒接触模型，模拟膏体流动行为较为理想。但是该模型设置的颗粒形状较为规则，考虑到膏体充填工艺会添加粗骨料，该模型存在局限性，不同颗粒尺寸是否对坍落度试验产生影响还需要进一步研究。在分析搅拌机中膏体的流动行为时，仅考虑充盈率以及搅拌转速对料浆混合度的影响，但叶片间距等因素也会影响膏体流变行为，这有待于进一步研究。