在半平面等分角上正割与余割函数幂的乘积和

贾云飞，郑德印

(杭州师范大学理学院，浙江 杭州 311121)

0 引言

在数论、三角函数逼近和插值、积分变换、离散傅里叶级数和数学物理方程求解等问题中常常会遇到一些在等分角上的三角函数求和问题.设T(θ)表示某一初等三角函数,那么对k的有限和(θk是等分上半平面的第k个等分角):

(1)

就属于这种情况.它已经被广泛地研究,比如,数学手册[1]就有如下的求和结果:

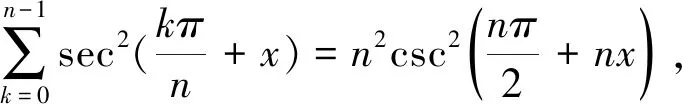
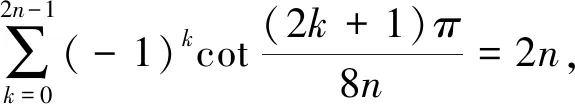
Byrne和Smith[2]使用Lagrange插值多项式证明了下面两类三角和

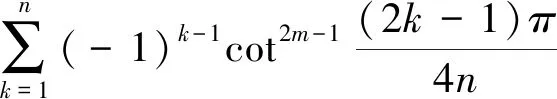
(2)

分别是n的2m-1和2m次的整数值多项式,并给出了多项式系数的递推关系.Hassan[3]使用样本定理和Lagrange型插值公式计算了大量的三角函数和,推广了文[2]的结果.文[3]还进一步指出,不仅有和值为n的整数值多项式的三角函数求和公式,也有和值为n的非整数值多项式的三角函数求和公式,其中两个简单例子如下:

最近,Annaby和Hassan[4]对这一问题又作了进一步研究,以Chebyshev多项式的零点为节点作Hermite插值得到了更多更复杂的三角函数和公式.

计算这类三角函数和的方法还有发生函数法和围线积分法.Chu和Marini[5]使用部分分式分解和发生函数方法系统地研究了类型(1)的三角函数求和问题,紧接着Berndt和Yeap[6]研究了此类三角函数和的两类基本类型:余切和与交错的余割和.王欣[7]将这一问题的研究向前推进了一步,在三角函数的角中增加了一个自由参数y,使用围线积分和发生函数两种方法,对这一问题作了系统研究,推广了文[5]的结果,得到了大量含有一个自由参数的此类三角函数求和公式.比如,对任意实数y,当n是正奇数时,有

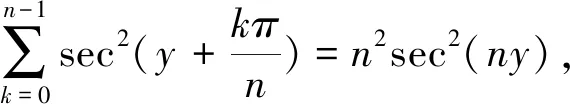
(3)

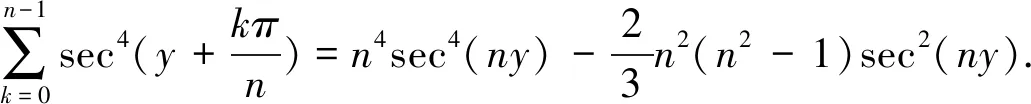
(4)

当n是正偶数时,有

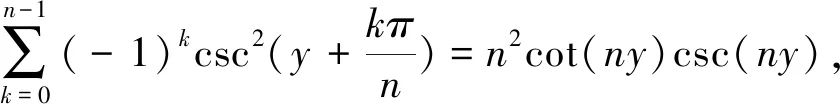
(5)

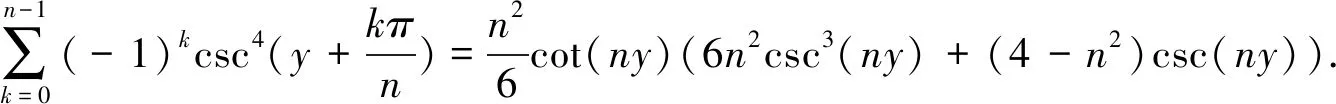
(6)

在文[7]的基础上,本文研究含有一个自由参数y的正割与余割函数幂的积的有限和,即

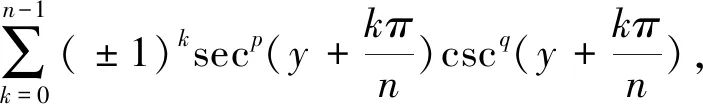
(7)

其中,p和q为非负整数.这类三角函数的求和问题在上述文献中虽有零星的个例,但没有进行系统的研究.比如,在文[7]中的(2.3.5):

通过简单的三角函数恒等变形,它可以变为

这两个和都是下文(44)的特殊情况.所以这里的研究内容是新的、具有一般性的.

在开始计算三角函数和之前,先给出4个引理,首先是正弦函数的降次公式.

引理1对任意的正整数m和实数θ,有下面的正弦函数的降次公式:

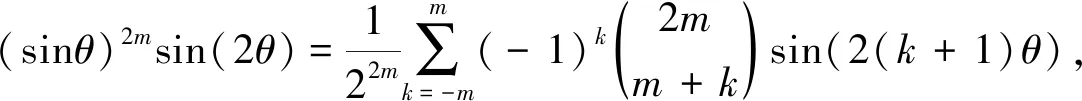
(8)

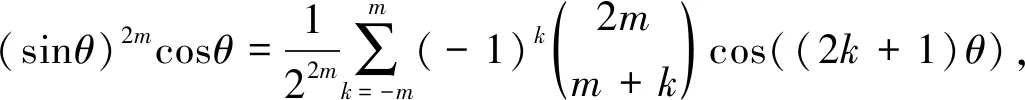
(9)

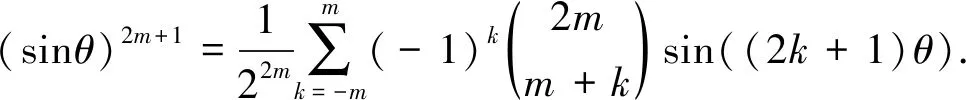
(10)

证明因为sinθ=(eiθ-e-iθ)/(2i),所以使用二项展开式定理,(sinθ)2m有展开式:

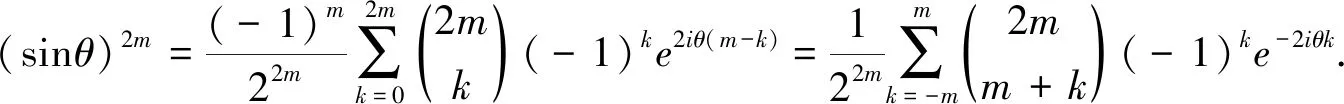
(11)

注意,将k换为-k,和式(11)不变.因此对等式(11)两边同乘以sin(2θ)=(e2iθ-e-2iθ)/(2i),可得式(8).类似地,对等式(11)两边同乘以cosθ=(eiθ+e-iθ)/2,可得式(9).等式(11)两边同乘以sinθ=(eiθ-e-iθ)/(2i),可得式(10).

□

使用JamesMoriarty的二项式恒等式,可以将反正弦函数与正弦函数或余弦函数的复合展开为简单的幂级数,它们实际上是属于2F1(z2)的超几何级数.这就是

引理2对任意实数λ,下面的函数可以展开为z的幂级数:

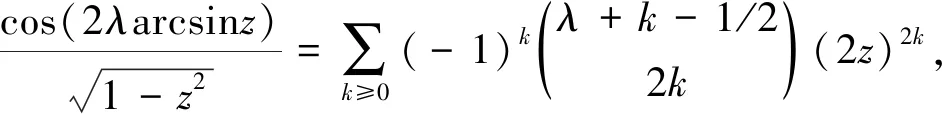
(12)

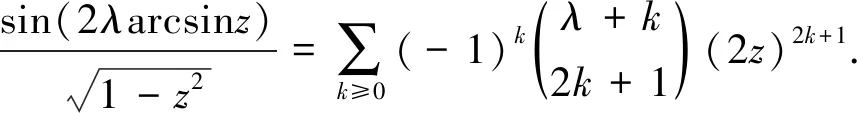
(13)

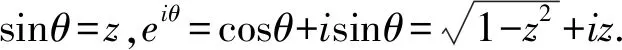
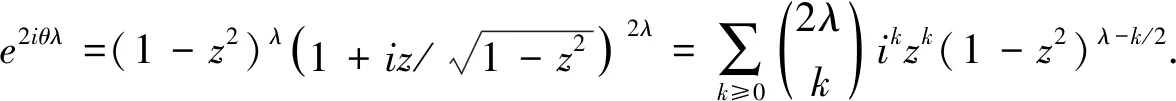
(14)

让k=2l得e2iθλ的实部:

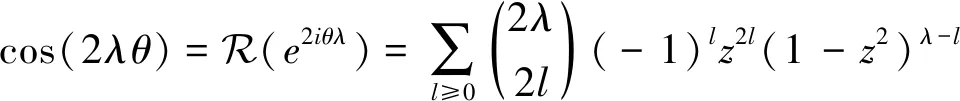
(15)

上式中对l的求和,用JamesMoriarty的求和公式[5]

可以化简,这样证得等式(12).

2) 在等式(14)中,让k=2l+1,可得e2iθλ的虚部:

上式中对l的求和,用求和公式[5]

可以化简,这样证得等式(13).此引理得证.

□

引理3下面的双变量形式幂级数展开式成立:

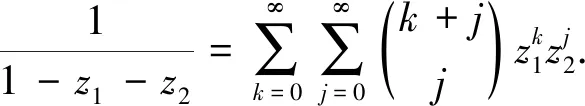
(16)

□

本文所要计算的正割与余割函数的和,能够求和的关键在于下面引理中的3个三角函数恒等式,这里使用部分分式分解方法给出了简单的证明.

引理4式[7,(2.1.3)和(3.1.5)]设y是一个使得下面各式有意义的实参数,那么下面3个关于θ的三角函数求和公式成立.

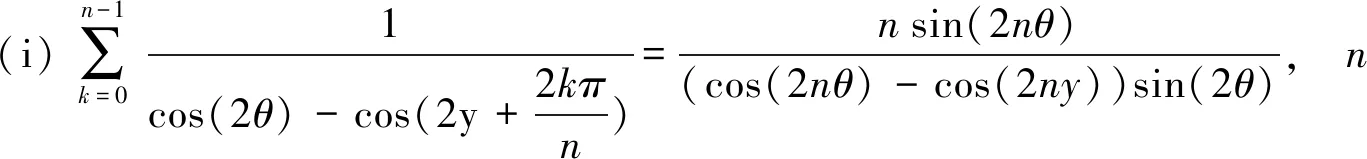
(17)

(18)

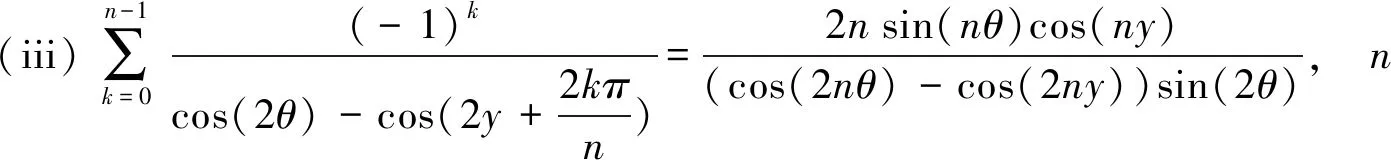
(19)

1 正割与余割函数幂的积的有限和

1.1 当n为正奇数时

定理1设y是一个使得下面的和式Un(p,q)有意义的实参数,那么对任意正奇数n,关于p和q的二重序列

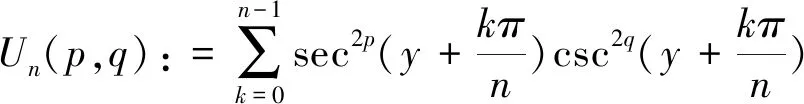
(20)

的双变量发生函数为

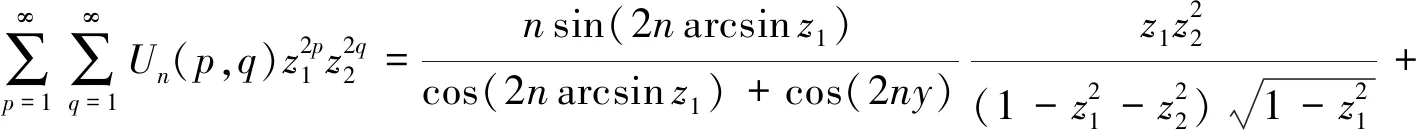
(21)

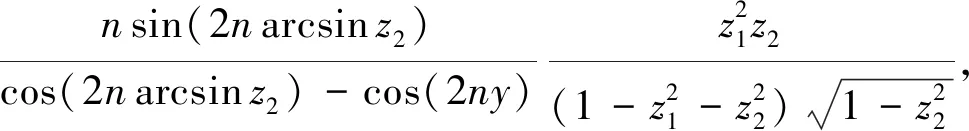
(22)

且对非负整数p和q,有如下的求和公式:

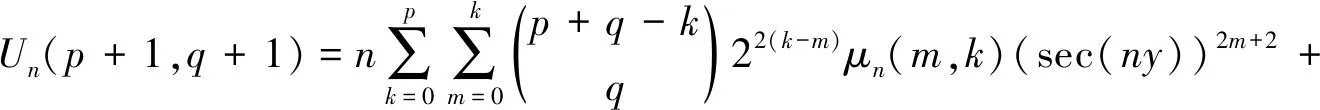
(23)

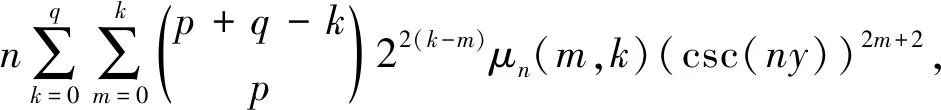
(24)

其中

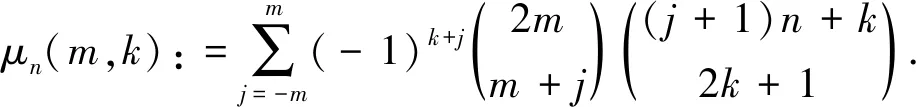
(25)

证明首先求Un(p,q)的双变量发生函数:

对上面求和项作部分分式分解,有

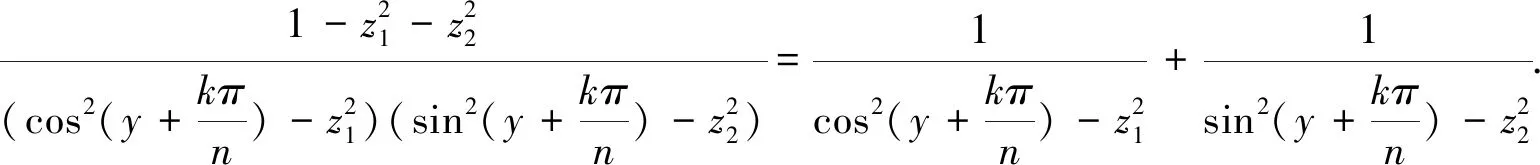
(26)

所以,Un(2p,2q)的双变量发生函数可以拆分为两部分和:

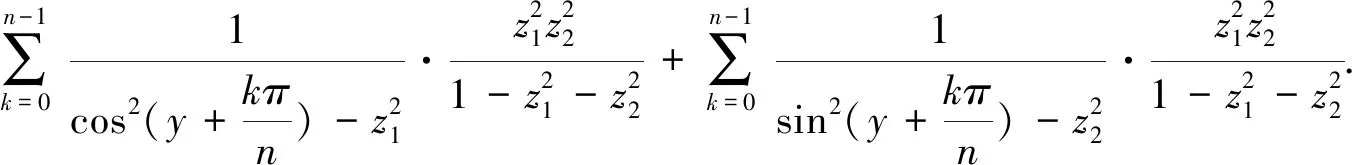
(27)

对第一部分作代换z1=cosα,同时使用求和公式(17),则有下面的求和结果:

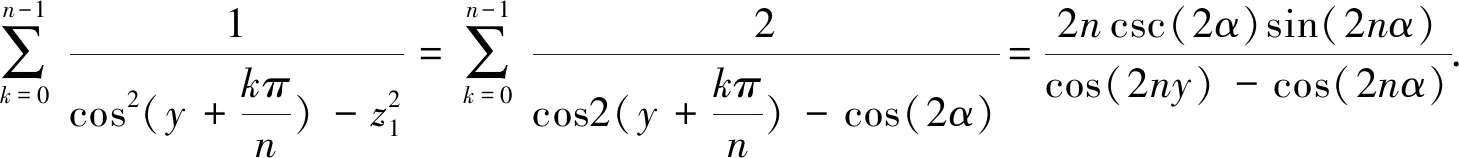
(28)

由于n是一个奇数,所以有

sin(2nα)=sin(nπ-2nα)=sin(2narcsinz1),

(29)

cos(2nα)=-cos(nπ-2nα)=-cos(2narcsinz1).

(30)

使用这些关系,把式(28)中的α的三角函数用z1表示,则有

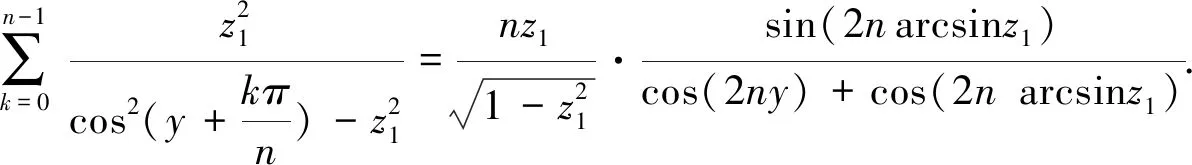
(31)

对式(27)的第二部分作代换z2=sinβ,那么有

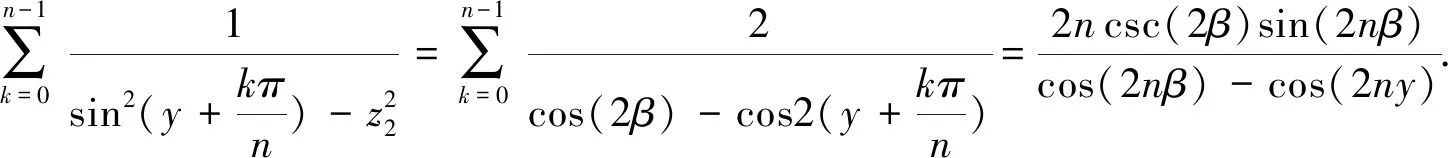
(32)

将β换为arcsinz2,则有

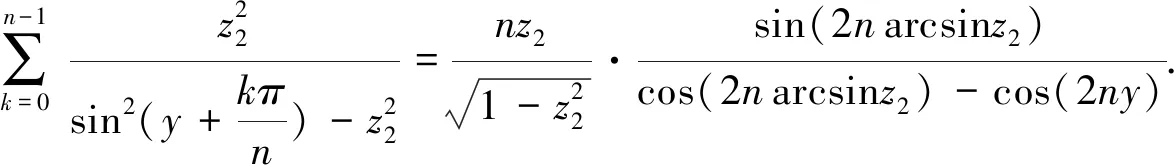
(33)

由式(27)、(31)和(33),立得发生函数(22).

下面证明式(24).这需要将发生函数(22)展开为z1和z2的幂级数.为了简单,设arcsinz1=α,则sinα=z1.使用幂级数展开式(1-x)-1=∑m≥0xm,有下面的展开结果:

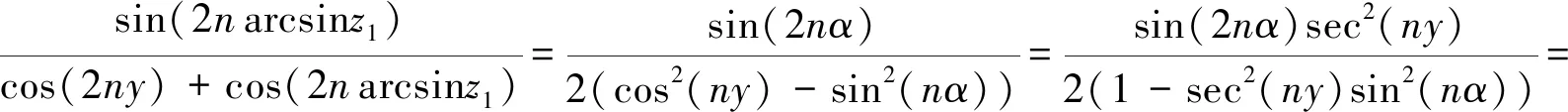
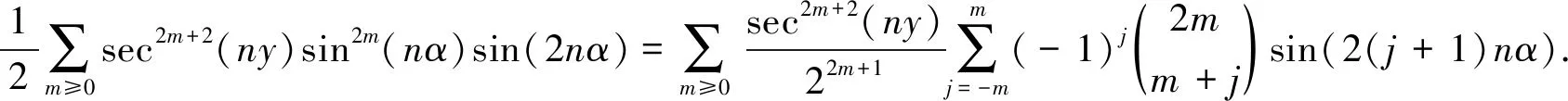
(34)

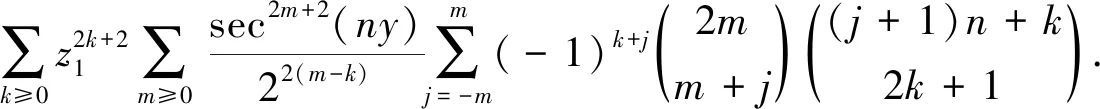
(35)

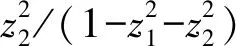
由于对式(21)等号右端的函数,把ny换为π/2-ny,z1和z2对换,即得式(22).因此,将式(23)中的ny换为π/2-ny,p和q对换,就得到式(24).这样定理得证.

□

例1在式(23)—(24)中,让p,q取0或1,则有

Un(1,1)=n2sec2(ny)+n2csc2(ny),

Un(1,3)=n2sec2(ny)+n6csc6(ny)-n4(n2-2)csc4(ny)+

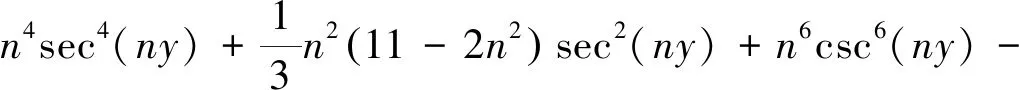
Un(3,3)=n6(csc6(ny)+sec6(ny))-n4(n2-4)(csc4(ny)+sec4(ny))+

注1(1)例1中的第一个公式就是文[7]中两个公式(2.2.3)和(2.3.3)在p=1时的和.

(2)Un(p,q)的对称性:将Un(p,q)的表达式中的sec和csc互换,可得Un(q,p)的表达式.

(3)当p=q时,公式(23)—(24)可简化为

1.2 当n为正偶数时

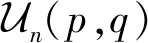
的双变量发生函数为

(38)

且对非负整数p和q,有如下的求和公式:

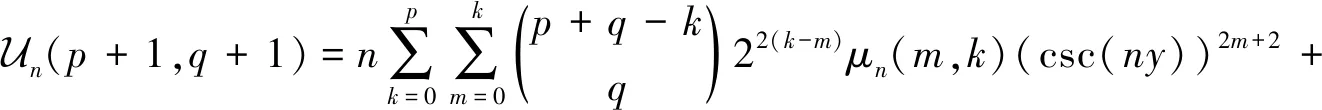
(39)

证明考察定理1的证明过程发现:当n由奇数变为偶数时,需要改变式(29)—(30)为

sin(2nα)=-sin(nπ-2nα)=-sin(2narcsinz1),

(41)

cos(2nα)=cos(nπ-2nα)=cos(2narcsinz1).

(42)

这样等式(31)应该被改写为

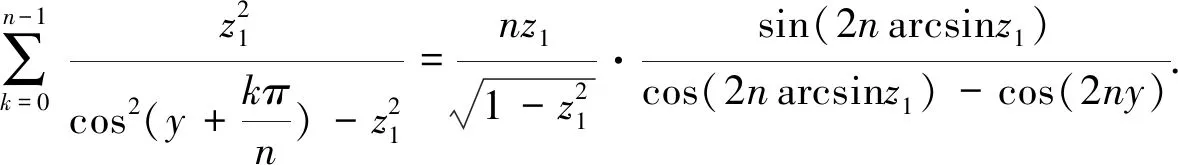
(43)

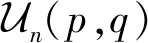
下面需要把发生函数(37)—(38)展开为z1和z2的幂级数来得到式(39)—(40).由于式(38)和(22)相同,所以式(40)和(24)相同.又因为在等号(37)的右端中将z1和z2互换,即得式(38).因此,把式(40)中的p和q互换,立得式(39)等号的右端.这样此定理得证.

□

例2在式(39)—(40)中,让p,q取0或1或2,则有

注2(1)例2中的第一个公式就是文[7]中两个公式(3.2.3)和(3.3.3)在p=1时的和.

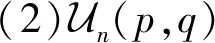
(3)当p=q时,公式(39)—(40)可简化为

2 正割与余割函数幂的积的交错和

2.1 当n为正奇数时

定理3设y是一个使得下面的和式Vn(p,q)有意义的实参数,那么对任意正奇数n,关于p和q的二重序列

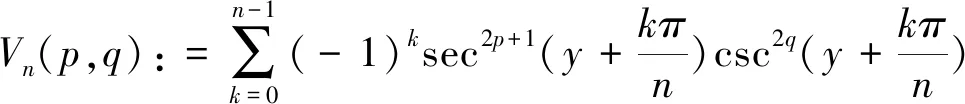
(44)

的双变量发生函数为

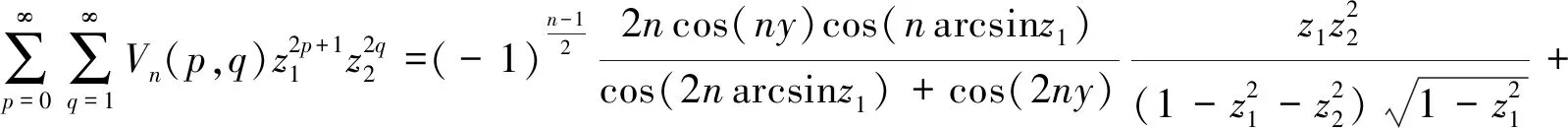
(45)

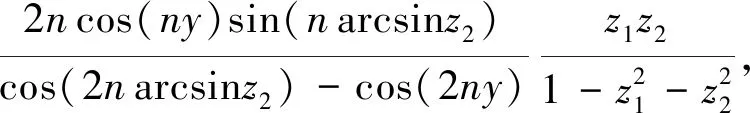
(46)

且对非负整数p和q,有如下的求和公式:

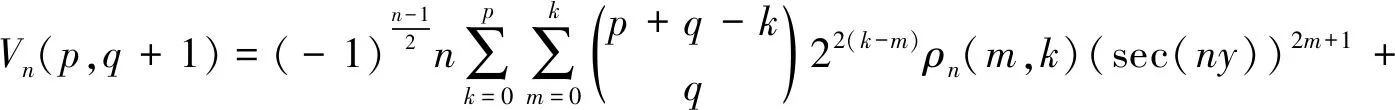
(47)

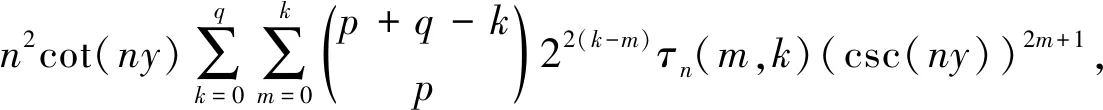
(48)

其中

证明首先求Vn(p,q)的双变量发生函数:

由部分分式分解式(26)知,Vn(p,q)的双变量发生函数可以拆分为下面的两部分和:

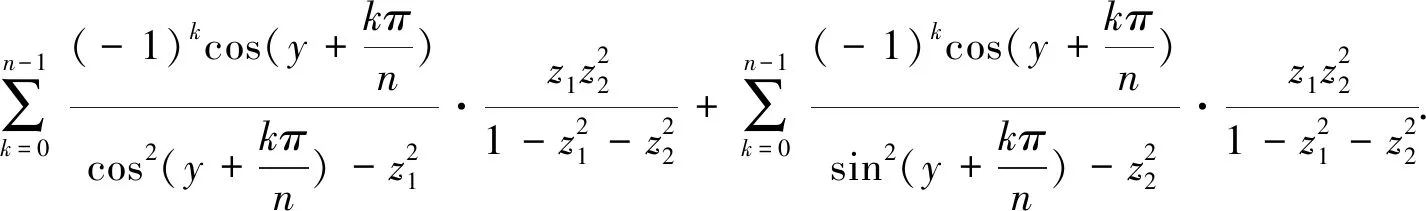
(49)

对第一部分作代换z1=cosα,同时使用求和公式(18),则有下面的求和结果:

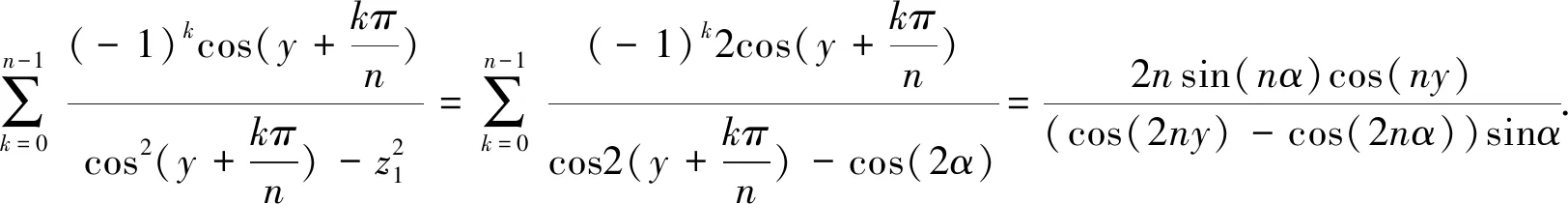
(50)

由于n是一个奇数,所以有

使用这些关系,把式(50)中α的三角函数用z1表示,则有

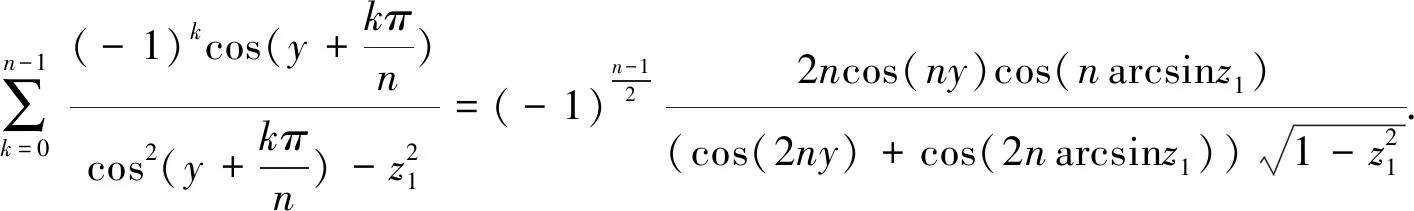
(51)

对式(49)中的第二部分和,作代换z2=sinβ,那么有

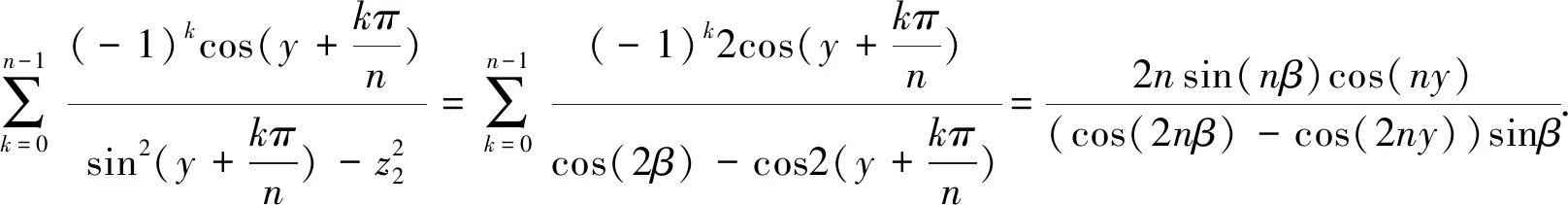
(52)

将β换为arcsinz2,则有

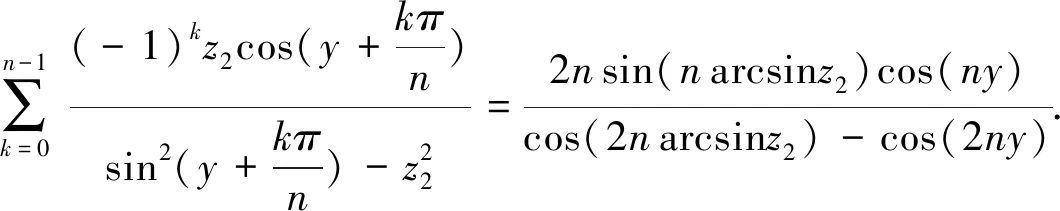
(53)

由式(49)、(51)和(53),立得发生函数(46).

下面证明式(48)，这需要将发生函数(46)展开为z1和z2的幂级数.为了简单,设arcsinz1=α,则sinα=z1.使用幂级数展开式(1-x)-1=∑m≥0xm,有下面的展开结果:

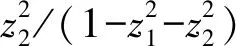
在式(34)中,将ny换为π/2-ny,sin(2narcsinz1)换为sin(narcsinz2),z1换为z2,同时使用公式(8),将sin((2j+1)nα)展开为z2的幂级数,那么有

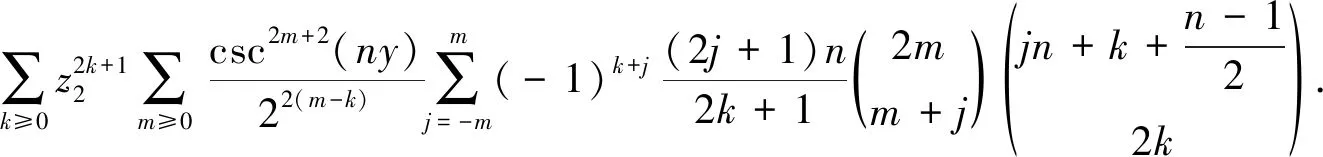
(55)

□

例3在式(47)—(48)中,让p取0,1,2,q取0或1,则有

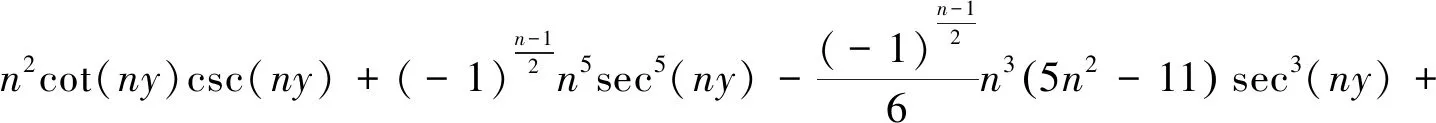
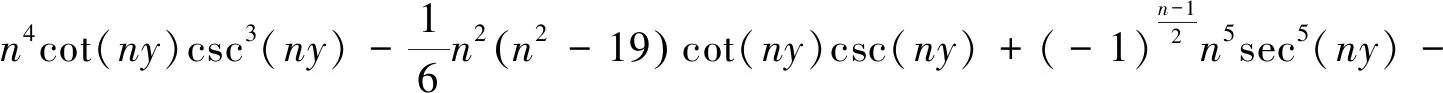
2.2 当n为正偶数时

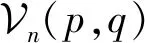
的双变量发生函数为

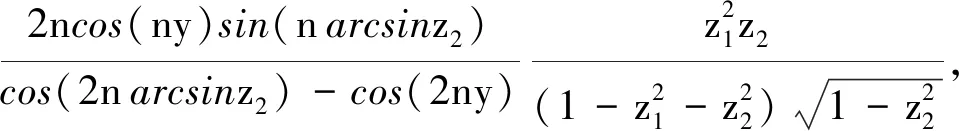
(58)

且对非负整数p和q,有如下的求和公式:

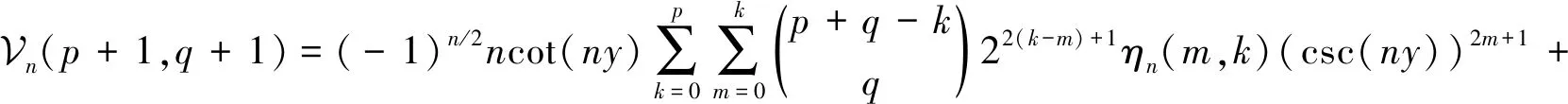
(59)

其中

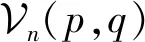
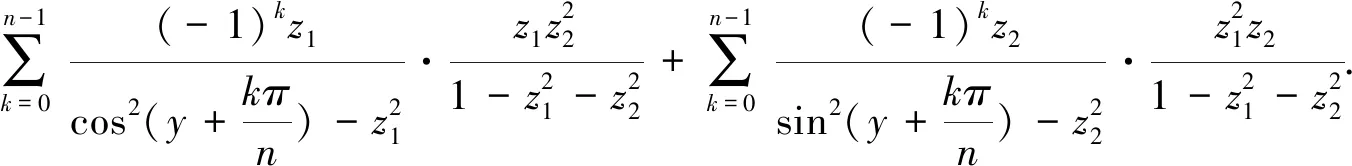
(61)

对第一部分作代换z1=cosα,同时使用求和公式(19),则有下面的求和结果:

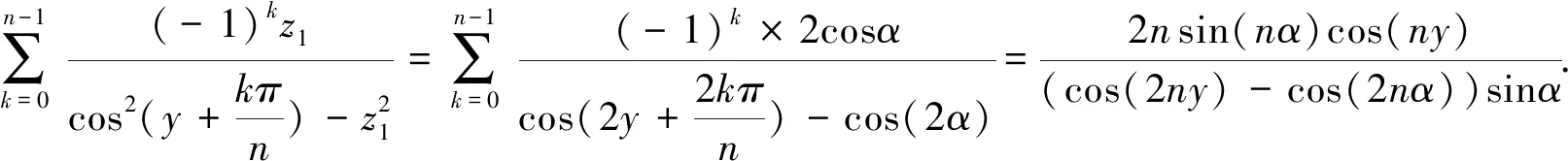
(62)

由于n是一个偶数,所以有

使用这些关系,把式(62)中α的三角函数用z1表示,则有

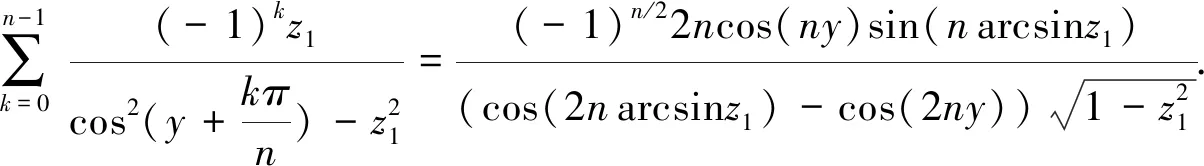
(63)

对式(61)中的第二部分作代换z2=sinβ,那么有

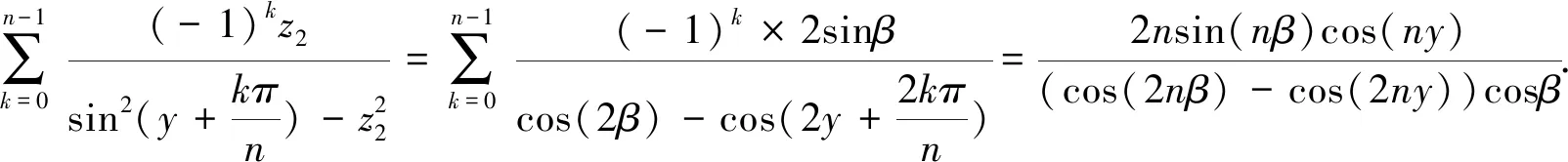
(64)

将β换为arcsinz2,则有

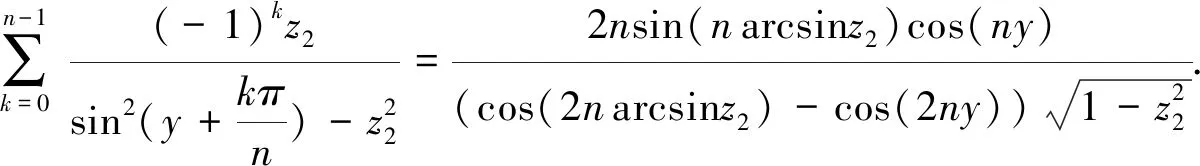
(65)

由式(61)、(63)和(65),立得发生函数(58).

类似于式(34),设arcsinz1=α,则有

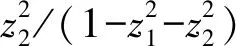
把式(57)中的(-1)n/2去掉,再将z1和z2对换,即得式(58).所以把式(59)中的(-1)n/2去掉,再将p和q对换,立得式(60).此定理得证.

□

例4在式(59)—(60)中,让p,q分别取0,1,2,则有

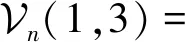
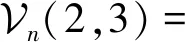
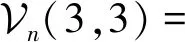
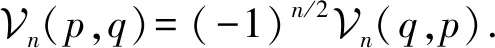
(2)当p=q时,公式(59)—(60)可简化为