基于电流型CMOS电路的新型和图转化方法

姚茂群，孙 曦，李聪辉

(杭州师范大学信息科学与工程学院，浙江 杭州 311121)

0 引言

当前，随着科学技术的不断进步，对信息处理能力需求的不断增加，集成规模不断扩大，集成度也始终遵循着“每三年增加一倍”的摩尔定律，因此降低功耗，提升速度，提高频率等一直都是集成电路研究迫切需要解决的问题，也是集成电路行业的发展趋势.而电流型电路在速度、功耗等方面一直有着较大的优势，另外，CMOS管处理电流信号也有较大优势，因此电流型CMOS电路成了当前集成电路研究的一大热点[1-3].

在电流型数字电路研究初期，理论以及电路设计方法比较匮乏，而阈算术代数系统的提出使得电流型CMOS电路的设计有了理论指导，使得整个电路设计流程更加清晰，其中和图的提出也大大地简化了电路设计，并且使得电路设计更加直观有效[4].

本文在原有和图转化方法的基础上，结合方程组的思想，提出了一种新的和图转化方法，该方法能够弥补原有方法在和图转化上的不足，为电流型CMOS电路设计提供方便.

1 阈算术代数系统

1.1 阈算术代数系统的概念、基本运算及性质

阈算术代数系统就是以非负运算(这里我们不做讨论) 、阈算术运算及算术运算为基本运算构成的代数系统.而阈算术函数就是其逻辑关系的解析，类似F=〈x〉t这种函数，我们就把它称为阈算术函数，而阈算术函数的值F为一切的自然数(0，1，2，…)，x称为信号变量，也可以用任意字母表示，如a,B,x等，取值范围为所有整数.而在阈算术函数中也有“·”和“+”运算，与逻辑函数中的基本一致，分别表示算术乘法运算和表示算术加法运算，“·”运算也可以省略.阈算术运算如下所示：

1) 高阈运算：

(1)

2) 低阈运算：

(2)

3) 双阈运算：

(3)

其中，x为整数[-m,…, 0,1,…,m],阈值t，t1，t2为[0.5 ,1.5,…,m-0.5],m为正整数[6].

1.2 和图的概念及特点

逻辑函数除了采用表格表示(真值表)与解析表示外，还可用图形表示.与逻辑函数的K图(卡诺图)相似，在阈算术代数系统中则用和图表示阈算术函数，从本质上讲和图包含K图，只不过图中的值不仅限于0，1，而是可以填入任意的整数.例如，阈算术函数F(x,y,z)=x+2y+4z的和图如图1所示.

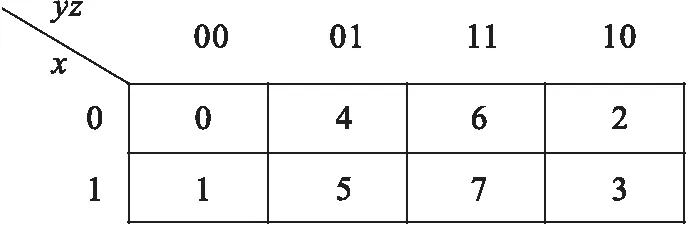
图1 F(x,y,z)=x+2y+4z的和图Fig.1 The He map of F(x,y,z)=x+2y+4z

通过和图来表示阈算术函数具有以下优点：

1) 使得阈算术函数的特点更加清晰明了，使得输入输出之间的关系能够得到直接的判定；

2) 阈算术函数之间的相互运算可以直接通过和图的运算实现[5-6].

1.3 和图的运算性质

和图的阈算术函数运算有阈算术运算(这里以双阈算术运算为例)，加法运算，减法运算和乘法运算，如图2—5所示.

图2 双阈算术运算Fig.2 Double threshold arithmetic

图3 加法运算Fig.3 Addition

图4 减法运算Fig.4 Subtraction

图5 乘法运算Fig.5 Multiplication

1.4 电流型CMOS电路的阈算术运算

1.4.1 高阈运算电路：F=〈x〉t，如图6所示.1.4.2 低阈运算电路：F=〈x〉t，如图7所示.

图6 高阈运算电路Fig.6 High threshold arithmetic circuit图7 低阈运算电路Fig.7 Low threshold arithmetic circuit

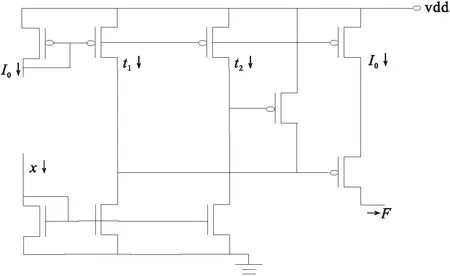
图8 双阈运算电路Fig.8 Double threshold arithmetic circuit

2 基于电流型CMOS电路的新型和图转化方法

通过和图，可以进行电流型电路的设计.首先，根据需要设计电路的逻辑函数，画出目标和图；其次，根据目标和图，构造一个尽可能和目标和图相同或者相似的和图；然后，再用一个或者多个和图与刚构造好的和图进行算术运算，得到新的目标和图，并求出阈算术函数表达式；最后，根据所得的阈算术函数表达式，设计相应电路.

然而，在实际的电路设计中，当和图比较复杂时，要完成上述的转化往往比较困难.为此，我们提出了一个基于和图的新型转化方法，它主要通过解方程的思路，获得目标和图对应的阈算术函数，能够在一定程度上使得和图的转化代数化，并且更加清晰和快速.

图9 F1(x,y,z)的和图Fig.9 The He map of F1(x,y,z)

图10 和图1Fig.10 The He map 1 图11 和图2Fig.11 The He map 2

图12 和图1的类似和图Fig.12 similar to the He map 1图13 和图2的类似和图Fig.13 similar to the He map 2

可以看到，使用和图转化方法得到的阈算术函数显然更加简单.不过，和图转化方法并不对所有的和图都成立，下面举例.

图14 F5(x,y,z)的和图Fig.14 The He map of F5(x,y,z)

将其代入高阈算术运算函数〈ax+by+cz〉t1或者低阈算术运算函数〈ax+by+cz〉t2，得如下方程组：

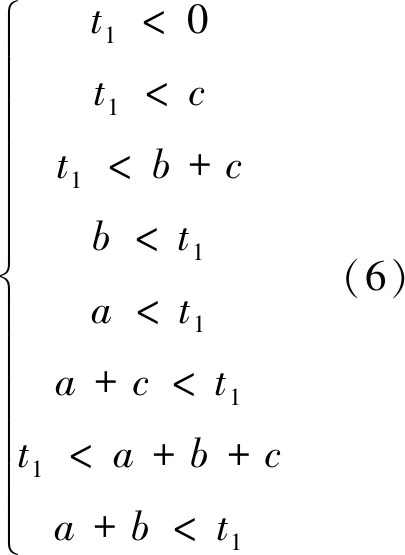
两个方程组均无解，则说明不能直接构造出阈算术函数，需要再通过阈算术运算得到.比如以上和图，则可由以下两个和图通过加法算术运算得到，如图15和图16所示.倘若不能直接得出其阈算术函数，可继续通过上述方法分别得到它们的阈算术函数表达式，然后再相加即可得到最终的阈算术函数.

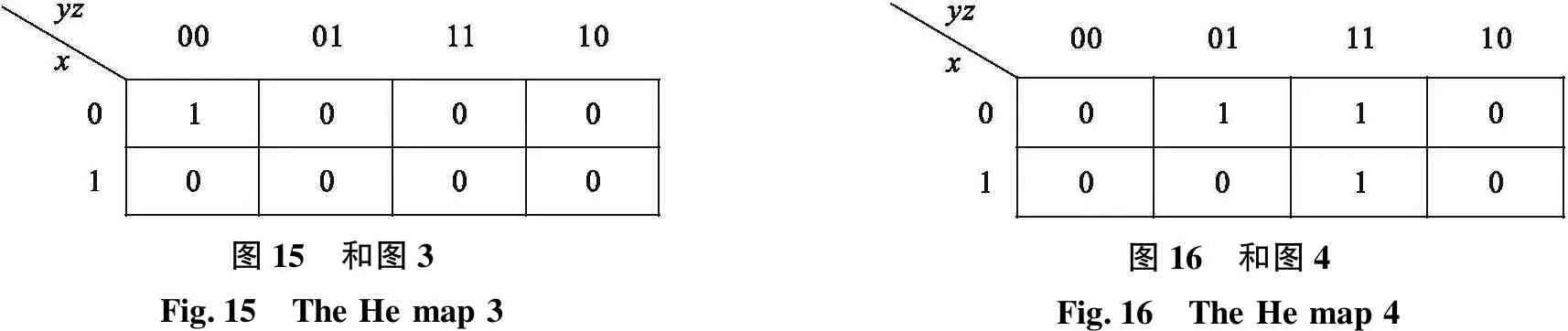
图15 和图3Fig.15 The He map 3图16 和图4Fig.16 The He map 4

考虑到当方程组比较复杂，计算比较繁琐的时候，可以通过计算机编程来求得方程的解.具体的流程如图17所示.经过大量的实验和计算，下面对这两种和图转化的方法进行总结和比较，如表1所示.

表1 和图转化方法比较Tab.1 Comparison with graph conversion method

3 基于新型和图转化方法的电流型CMOS全加器设计

全加器是组合电路中基本的元器件，也有着广泛的应用.它能够将加数、被加数和低位来的进位信号相加，并根据求和结果给出该位的进位信号.设输入端x(被加数输入),y(加数输入)，输出端为S(本位和输出), C(进位输出).其输出端真值表对应的两个目标和图如图18和图19所示.

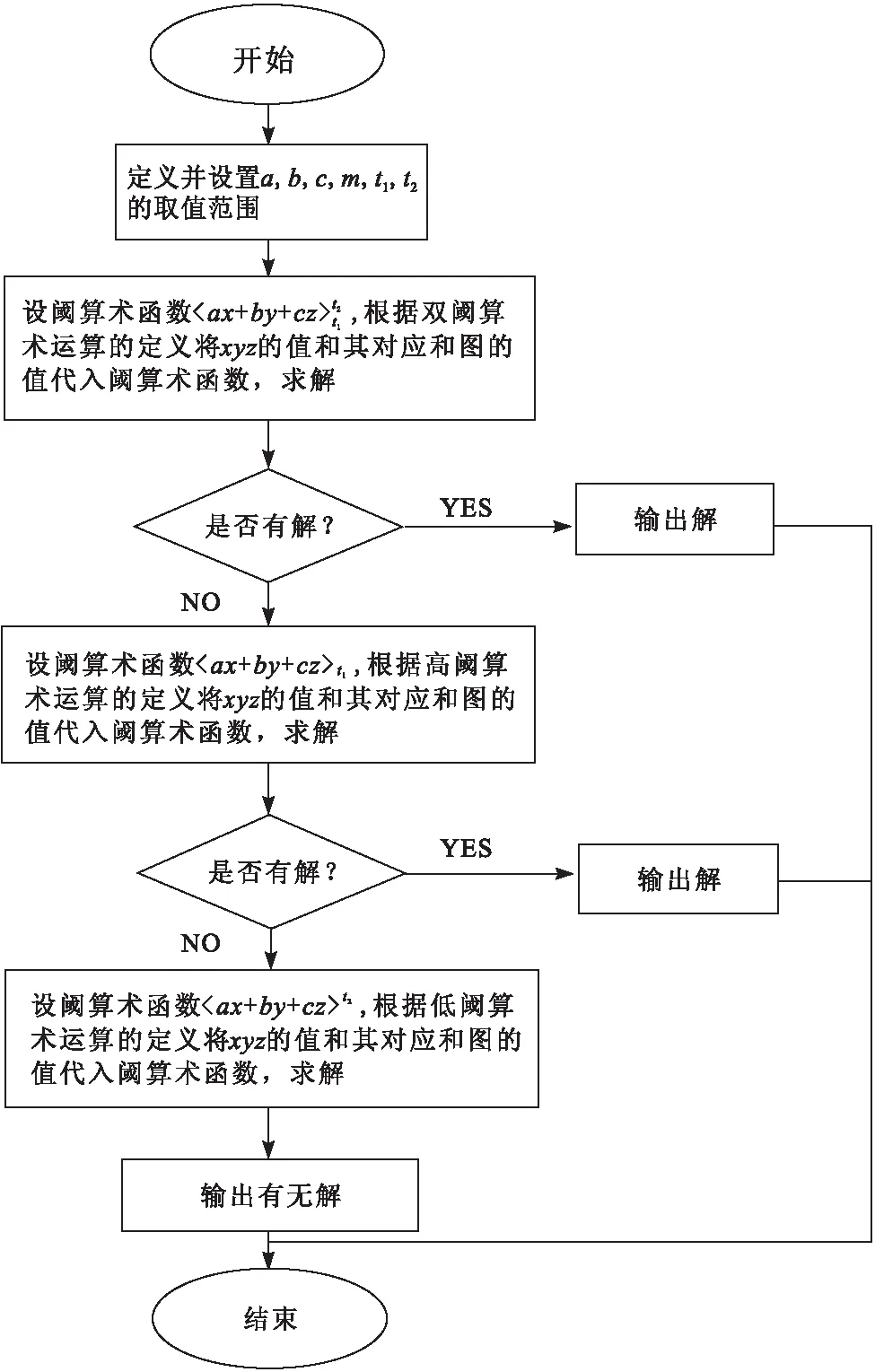
图17 流程图Fig.17 Flow chart

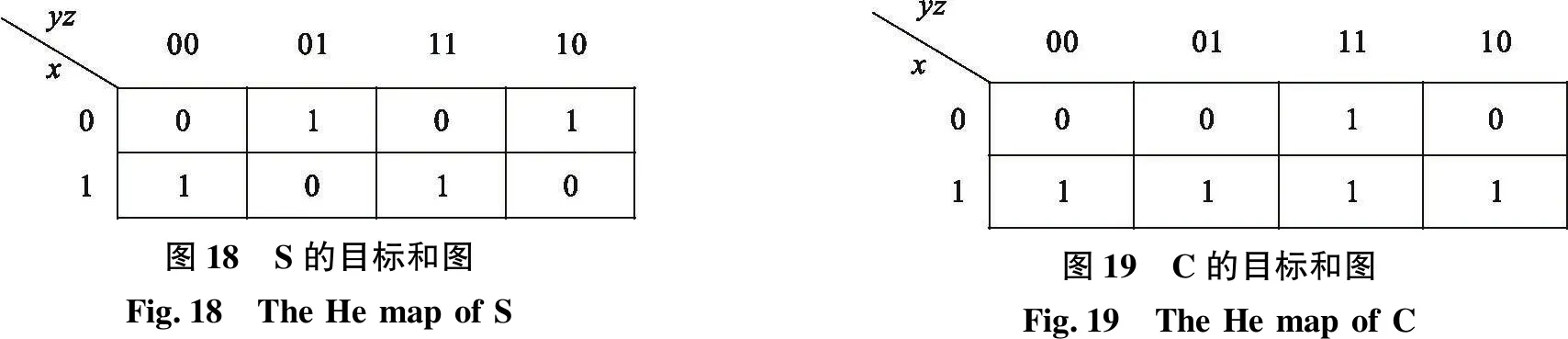
图18 S的目标和图Fig.18 The He map of S图19 C的目标和图Fig.19 The He map of C

根据S的目标和图，很难构造阈算术函数，因此采用新提出的和图转化方法去求解对应的阈算术函数.第一步，设最终的阈算术函数为高阈算术运算函数F18(A,B,C)=〈ax+by+cz〉t1；第二步，将xyz的值以及其对应的和图的值代入，并且a，b，c为整数，t1∈(0.5,1.5,…,m-0.5)，可得如下的方程组：

经过计算，该方程组无解.第三步，继续设最终的阈算术函数为低阈算术运算函数，列方程组，同样解得方程组无解，再设成双阈算术运算函数，列方程，也求方程组无解.说明该和图不能直接化成单个阈算术函数的形式，因此，考虑将该和图分解.分解后的和图如图20和图21所示.

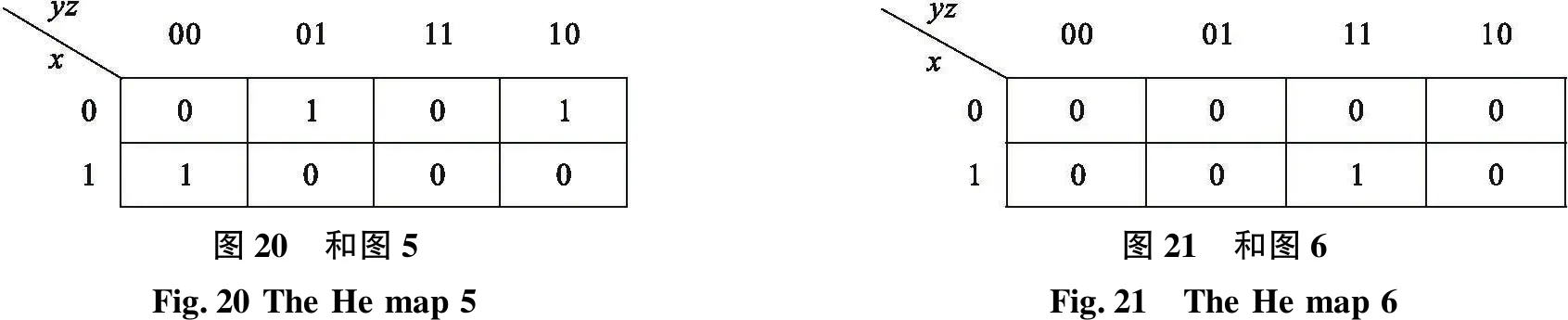
图20 和图5Fig.20 The He map 5图21 和图6Fig.21 The He map 6

图22 全加器电路图Fig.22 Full adder circuit diagram

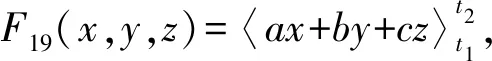
根据C的目标和图，同样采用新的和图方法，可以求得最终的阈算术函数为F22(x,y,z)=〈x+y〉1.5.通过S和C的阈算术函数表达式，设计出的电流型CMOS全加器电路如下图22所示.

采用TSMC180 nm工艺参数在软件Hspui A-2008.03上对电路进行Hspice模拟[7-9]，对应于逻辑值0的电流为0，对应于逻辑值1的电流为10 μA，这里的vdd均采用1.8 V，模拟得到的电路瞬态特性如图23所示，模拟结果分析表明，所设计的全加器电路具有正确的逻辑功能，且电路的瞬时功耗较低，为206.4 μw.

图23 电路瞬态特性图Fig.23 Circuit transient characteristic diagram

4 结论

本文通过解方程的思路，提出了一种基于和图的新型转化方法，该方法相较于原方法，在处理复杂和图，快速将和图化简为单个阈算术函数等方面有着较大优势，并且能通过计算机编程实现提高计算效率.另外，通过该方法，本文设计了一种基于电流型CMOS电路的全加器，经过模拟分析结果证明，所设计电路结构简单，功耗较低[10].