基于灰狼优化SVR的风电场功率超短期预测

徐炜君

(东北石油大学秦皇岛校区电气信息工程系， 河北 秦皇岛 066004)

0 引 言

伴随着化石能源的逐渐枯竭及环境危机的日益剧烈，可再生能源的发展及应用得到了世界各国的广泛关注.作为可再生能源中的一员——风能的利用呈逐年上升的趋势，世界各国风机的装机容量迅速增长.据中国可再生能源学会风能专业委员会统计：2018年全国(除港、澳、台地区外)新增装机容量 2114.3万kW，同比增长7.5%；累计装机容量约2.1亿kW，同比增长11.2%，保持稳定增长态势[1]，因此如何利用好这些风能将对我国的节能减排战略产生重要的影响.然而由于日照、地形、温湿度、气压等环境因素的影响，风速具有较大的随机性和波动性[2]，这对电网的安全和供需平衡带来了巨大的挑战[3-4].

按照时间尺度来分，风电功率预测的时间跨度可以从几秒到几个月[5].按照国家电网公司2016年发布的《风电功率预测功能规范》，从次日零时起3 d为短期预测，时间分辨率为15 min；15 min—4 h为超短期预测，其时间分辨率不小于15 min[6].研究表明，超短期预测的精度直接影响风机机组组合、电网调度等操作，并对电网的安全、经济运行起着重要的作用.

研究表明，对于数据驱动的预测方法来说，输入数据维度的提高,更有利于探索风能的动态变化规律[7].同时，风力变化过程在短期具有惯性的特点[8].因此，结合目前的研究现状，用山西省朔州市某风电场的温度、湿度、气压、风向、风速等历史数据构建输入模型，采用灰狼优化算法(Grey Wolf Optimizer，GWO)优化支持向量回归机(Support Vactor Regerssion，SVR)的参数(C，g)，进而建立风电功率的超短期预测模型，实验对比结果表明其预测精度和预测时间都有显著的提高且稳定性好.

1 风电场数据建模及数据预处理

风电场一般由若干台风力发电机组成，各个风机的分布主要依地势、尾流效应、主风向等因素而定.由于风能随机性的影响，风电场各个风机的发电功率不能与风力相匹配，因此风电场的风电功率预测应着重考虑整个风电场的风电特性，而风电场中的测风塔最能反映这一特性.目前业界比较认可的风电功率预测方法有两种：一是先预测风速，然后根据风电场的功率曲线得到风电场的输出功率；二是直接预测其输出功率[9].本文采用第一种方法.

1.1 影响风电场风机出力的因素

风机的输出功率可以表示为[10-11]：

P=CpAρv3/2

(1)

其中：P为风机输出功率，单位为kW；Cp为风轮的功率系数；ρ为空气密度，单位为kg/m3；A为风轮扫掠面积，单位为m2；v为风速，单位为m/s.由式(1)可知，风机出力和风速的三次方以及空气密度成正比，而空气密度与气压、温度、湿度有关，可以表示为[12]：

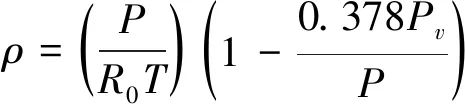
(2)

其中，ρ为空气密度，P为固定时间内测量的干燥空气平均气压，R0为干燥空气的气体系数，T为固定时间内的平均温度，T=Tc+273.15，Tc为实际温度，Pv的计算如式(3).

(3)

式中，C0=6.1078,C1=7.5,C2=237.3分别为特滕斯公式(Tetens Formula)的系数.PH%为相对湿度，定义为实际水蒸气压力和饱和水蒸气压力的比值.

综合式(1)—(3)可以看出，气压、温度、湿度的变化以及风速都会影响风机的输出功率，因此在进行风电场数据建模时，必须考虑上述影响因素.

1.2 风电场数据建模

以山西省朔州市某风电场测风塔的日监测气象数据作为预测模型的输入样本集.考虑到1.1节所述的影响因素，构成如下16维向量：

(4)

其中：t为采样时刻点(每5 min采样一次)，v100avg，v100max，v100min，v50avg，v50max，v50min，v10avg，v10max，v10min，分别为测风塔100 m、50 m及10 m高处的平均、最大和最小风速，a90avg、a70avg、a10avg为测风塔100 m高处风向的平均、最大和最小值，RH、T、P分别为湿度、温度和气压.

考虑到当地夏季的气候变化比较剧烈，因此选用2019年7月1日—7月5日5 d的日监测数据作为建模数据，每天以5 min为间隔进行数据采样，最终得到1个16×1 440的数据.

1.3 数据预处理

风电场功率预测模型构建时，取前4 d的数据(7月1日至7月4日)作为训练样本，第5天(7月5日)的数据作为测试样本，而这些数据其各维量纲、取值范围各不相同，为了使各维分量在实际的预测过程中具有相同的地位，必须将输入数据变换到同一范围，这就需要对其各维分量进行归一化预处理[13]，归一化的方法如式(5)，归一化后数据的取值范围统一为[-1,1].

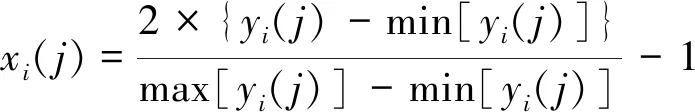
(5)

其中：i=1,2,…,16，j=1,2,…,1440，yi(j)为分量，max[yi(j)]，min[yi(j)]分别为第i个分量的最大和最小值，xi(j)为归一化后的分量值.

2 基于GWO-SVR预测模型的构建

2.1 支持向量回归机(SVR)

支持向量回归机(SVR)由 Vapnik[14]于1995年首次提出，其核心思想是通过非线性变换φ(x)将输入向量映射到一个高维特征空间H中，然后在高维特征空间中进行线性回归，从而得到原空间的非线性回归特性，其映射函数可以表示为：

y=wTφ(x)+b

(6)

其中，w和b为函数系数.支持向量回归拟合问题可以表示为目标函数优化问题，其对应的优化目标函数为[15]：

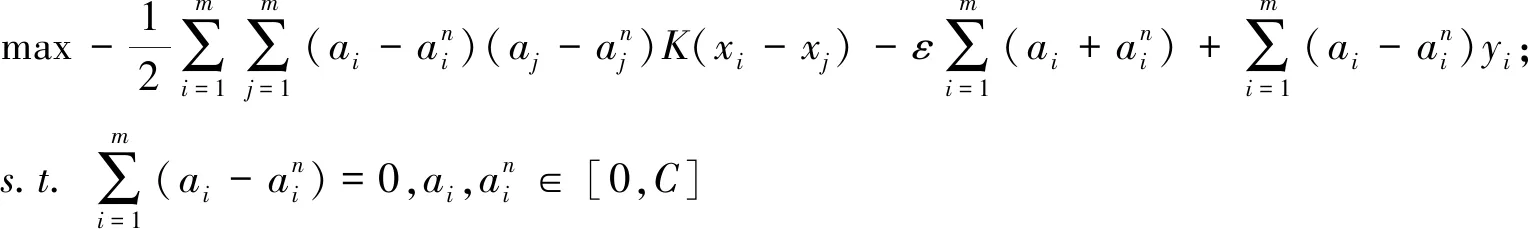
(7)

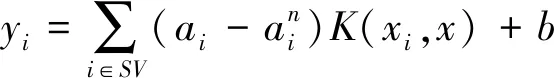
(8)

由式(7)(8)可见,只要选取合适的惩罚因子C、不敏感损失参数ε和核函数参数g便可以确定 SVR 的具体形式，从而对控制对象进行准确的预测.因此，影响 SVR性能的关键参数有惩罚因子C、不敏感损失参数ε和核函数参数g,而核函数类型的选取会直接影响预测结果，同时考虑到核函数参数的数量对预测模型复杂程度的影响，本文选择能够实现非线性映射的径向基函数(radial basis function，RBF)作为SVR的核函数，其表达式为：

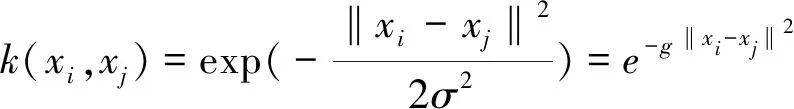
(9)

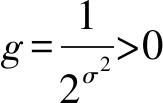
2.2 灰狼优化算法

灰狼优化算法(Grey Wolf Optimizer, GWO)是澳大利亚学者Mirjalili[16]于2014受灰狼捕食行为的启发，提出的一种群智能优化算法.灰狼是一种位于食物链顶端的群居性食肉动物，其族群数量一般在5～12只，其族群有着非常严格的社会等级制度，在捕猎过程中分工明确、协同合作.GWO算法根据上述特性，将狼群分为α、β、δ、ω4种，α狼是领导者(最优解)，β狼和δ狼协助α狼对狼群的进行管理及捕猎过程中的决策问题，同时也是α狼的候选者，ω狼主要协助α、β、δ对猎物进行攻击.灰狼捕猎的过程分为包围、追捕、攻击3个阶段，最终捕获猎物(获得全局最优解)[16].具体算法描述如下：

1)包围猎物(Encircling Prey)

捕猎过程中，将灰狼包围猎物的行为定义为：

D=|C·Xp(t)-X(t)|

(10)

X(t+1)=Xp(t)-A·D

(11)

其中，t为当前迭代，A和C为协同向量，Xp(t)为猎物的位置向量，X(t)为灰狼的位置向量.A、C的计算如下：

A=2a·r1-a;C=2r2

(12)

其中，a在迭代过程中线性递减且递减范围为[2,0]，r1,r2是[0,1]范围内的随机向量.

2)狩猎(Hunting)

当灰狼识别出猎物的位置后，β,δ狼在α狼的带领下对猎物进行包围.实际优化问题的最优解(猎物的位置)是不确定的，因此为了模拟灰狼的狩猎行为，假设α、β和δ更了解猎物的潜在位置，以目前α、β和δ的位置代表3个最优解，并利用这三者的位置来判断猎物的所在，同时其他灰狼个体(包括ω狼)依据最优灰狼个体的位置来更新其位置，逐渐逼近猎物[17].这一过程的数学模型描述如下：

(13)

其中，Dα,Dβ,Dδ表示α、β和δ狼和其他狼之间的距离，Xα,Xβ,Xδ是α、β和δ狼的当前位置，C1,C2,C3是随机向量，X是当前灰狼的位置.式(14)定义了ω狼朝α、β和δ前进的步长、方向及ω狼的最终位置.

达沙替尼和伊马替尼的不良反应信号检测研究…………………………………………………… 吴邦华等（20）：2840

(14)

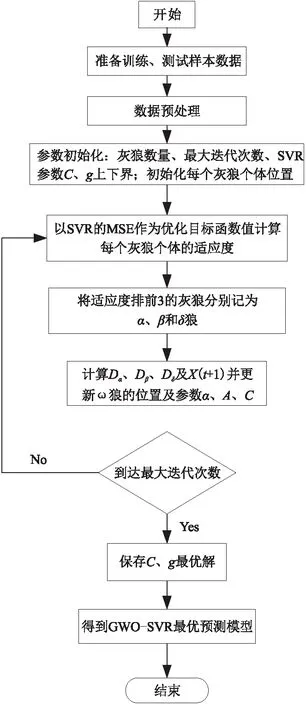
图1 GWO-SVR预测模型构建流程图Fig.1 GWO-SVR forecast model construction flow chart

3)攻击(Attacking Prey)

攻击意味着得到最优解.这一过程主要通过式(12)中a值的递减来实现.当a在[2,0]区间线性递减时，A值在[-a,a]区间变化.当|A|<1时，狼群会更加接近猎物；|A|>1时，狼群会背离猎物.

2.3 GWO-SVR预测模型的构建

GWO-SVR预测模型的构建流程如图1.算法主要步骤为：

1)将测风塔采集到的16×1 440数据分为16×1 152训练数据和16×288测试数据并进行数据的预处理；

2)初始化灰狼数量、最大迭代次数、SVR参数C、g的上下界、狼群中每个灰狼的位置；

3)以SVR的均方误差MSE作为目标函数，计算每个灰狼个体的适应度，并将适应度排前3的灰狼位置记为Xα,Xβ,Xδ；

4)依据公式13、14计算Dα,Dβ,Dδ及X(t+1)并更新ω狼的位置及参数α、A、C；

5)判断是否到达最大迭代次数，如果达到则保存C、g最优解，否则返回步骤3；

6)得到GWO-SVR最优预测模型.

3 实验分析

为验证本文提出算法(GWO-SVR)的优越性，分别使用遗传(GA)算法、粒子群(PSO)算法、GWO算法优化SVR的参数C、g并对风电场的风速进行预测，分别从优化结果及预测结果两个方面比较3种方法.

3.1 优化结果分析

以适应度作为评价指标.图2—图4分别为GA、PSO及GWO优化的适应度曲线.图5为3种优化算法适应度曲线的比较，通过图5可以看出，GWO的优化效果和稳定性明显优于GA和PSO算法.从时间尺度考虑，GA耗时最长(平均为111.38 s)，PSO次之(平均为37.47 s)，GWO最短(平均为11.59 s).表1为3种优化算法的结果.

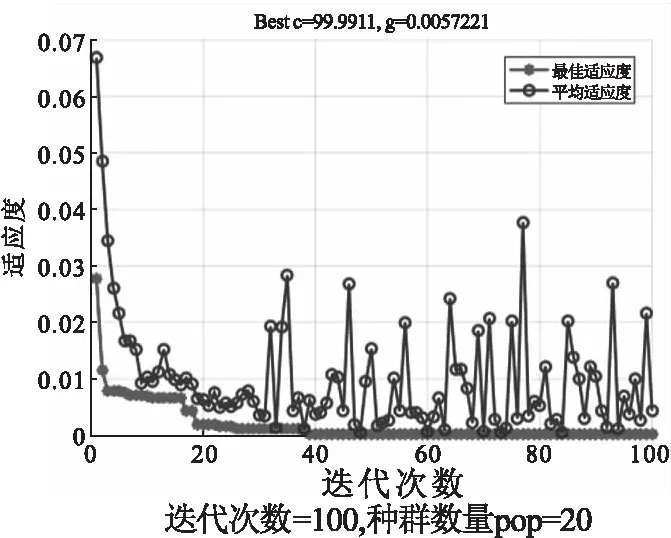
图2 GA优化适应度曲线Fig.2 GA optimization fitness curve

3.2 模型预测结果分析

用3.1得到的SVR最优参数，对风电场的风速分别进行预测，3种算法的预测结果如表2.图6为GWO-SVR的风速预测曲线.由表2可以看出GWO-SVR预测模型的均方根误差(RMSE)比GA-SVR和PSO-SVR分别降低了2.38%和1.4%，并且其拟合度(R2)在三者中也是最好的.通过上述分析可以看出，GWO-SVR风速预测模型稳定性好、预测精度高、预测时间短.

图3 PSO优化适应度曲线 Fig.3 PSO optimization fitness curve图4 GWO优化适应度曲线 Fig.4 GWO optimization fitness curve图5 适应度曲线比较Fig.5 Comparison of fitness curves图6 GWO-SVR的风速预测曲线Fig.6 Wind speed prediction curve of GWO-SVR

表1 参数优化结果Tab.1 Parameter optimization resultsSVR参数GAPSOGWOC99.99111.09431.478g0.00572210.010.01表2 预测误差分析Tab.2 Prediction error analysis预测方法RMSE%R2%T/sGA-SVR8.6289.69111.38PSO-SVR7.6493.1337.47GWO-SVR6.2495.6111.59

4 结论

针对风力发电随机性和波动性影响电网的安全和供需平衡等问题，考虑风电场气压、温度、湿度等气象因素和风速对风机输出功率的影响，用山西省朔州市某风电场测风塔测得的温度、湿度、气压、风向、风速等历史气象数据构建输入模型，采用灰狼优化算法(GWO)优化支持向量回归机(SVR)的参数(C，g)，进而建立风电场功率的超短期预测模型，实验比较结果说明：GWO-SVR预测模型稳定性好、预测精度高、预测时间短.