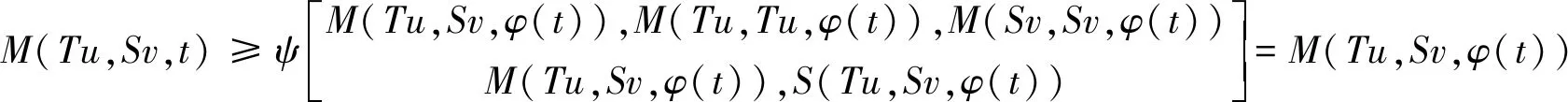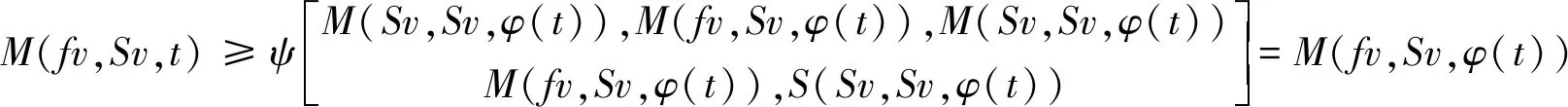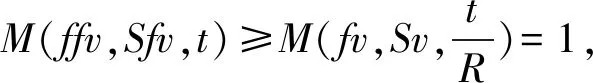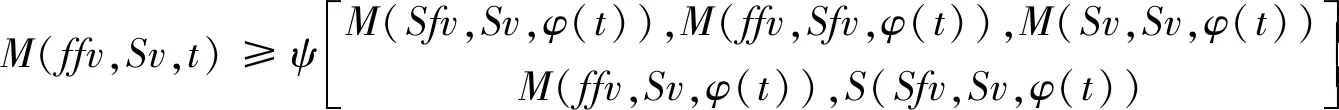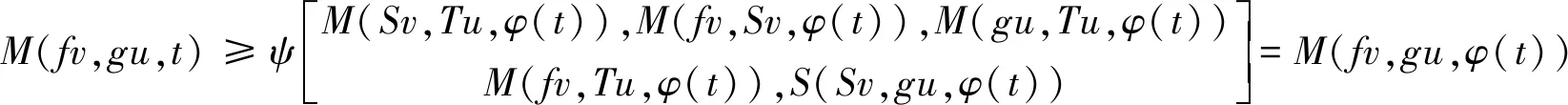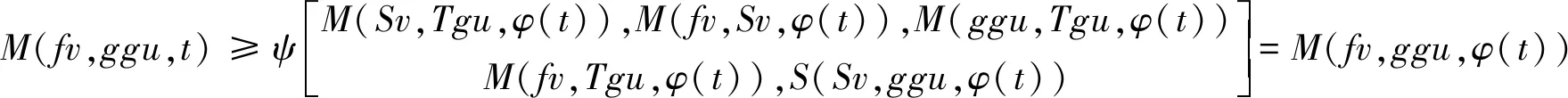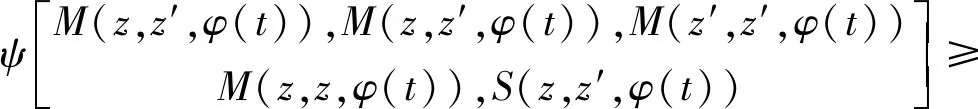模糊度量空间中几种压缩映象的公共不动点定理

孙玉鑫，谷 峰

(杭州师范大学理学院，浙江 杭州 311121)

1 引言和预备知识

1975年Kramosil和Michalek[1]首次提出模糊度量空间的概念，随后George和Veeranani[2]修改了文献[1]中模糊度量空间的概念，并得到了该空间中的Hausdorff拓扑. 1994年Mishra[3]等人在模糊度量空间中给出了相容映象对的概念，许多学者相继给出了多种相容映象的类型[3-6]，并证明了一些公共不动点定理. 2012年Imdad[7]和Sintunavarat[8]分别提出了非相容映象对和(Ag)型R-弱交换的概念.

首先我们给出模糊度量空间中的基本概念.

定义1[9]称二元算子*:[0,1]×[0,1]→[0,1]是连续的t-范数,如果以下条件被满足：

(1) *满足交换律和结合律;

(2) *是连续的;

(3) 对∀a∈[0,1],有a*1=a;

(4)a*b≤c*d,∀a≤c,b≤d,a,b,c,d∈[0,1].

常见的t-范数主要有a*b=ab,a*b=min(a,b)和a*b=max(a+b-1,0).

定义2[1]一个三元组(X,M,*)称为模糊度量空间,其中X是任意的非空集合,*是一个连续的t-范数,M是作用在X2×[0,∞)上的模糊集并且满足以下条件：对于∀x,y,z∈X,t,s>0,有

(1)M(x,y,0)=0;

(2)M(x,y,t)=1⟺x=y;

(3)M(x,y,t)=M(y,x,t);

(4)M(x,y,t)*M(y,z,s)≤M(x,z,t+s);

(5)M(x,y,·):[0,∞)→[0,1]是左连续的.

注1文献[10]中指出模糊度量空间中有以下条件成立：

例1[2]设(X,d)为度量空间,a*b=min(a,b),对所有的x,y∈X,t>0,定义

则M是一个模糊度量.

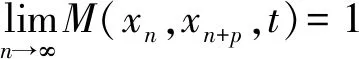
如果每个G-柯西列在X中都收敛,则称该模糊度量空间是G-完备的.

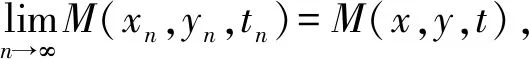
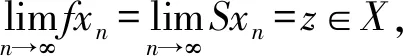
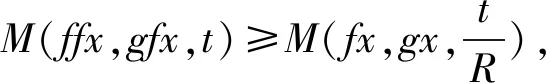
引理1[10]设(X,M,*)是模糊度量空间,那么M在X2×(0,∞)上是连续的.

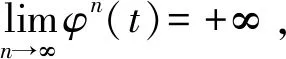
如果函数φ满足条件(Φ),则对∀t>0,n∈N+,有φn(t)>φn-1(t)>L>φ(t)>t.

刘展[13],李亚琼[14]和周书行[15]等人先后在概率度量空间、度量空间以及G-度量空间中证明了有关非相容映象对的公共不动点定理.受以上文献的启发,本文主要利用非相容映象对和(Ag)型R-弱交换的概念,在既不需要映象对连续也不需要空间完备的条件下,在模糊度量空间中建立了几类新的压缩映象的公共不动点定理,进一步推广和改进了已有文献的相应结果.

2 主要结果

引理2在模糊度量空间(X,M,*)中,若对所有的t>0,n∈N+,有

M(x,y,t)≥M(x,y,φ(t))≥L≥M(x,y,φm(t)),x,y∈X.

其中φ满足条件(Φ),则x=y.

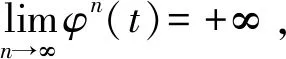
M(x,y,t)≥M(x,y,φ(t))≥…≥M(x,y,φm(t)),x,y∈X.

对∀t>0,此时M(x,y,t)=1,则x=y.

定理1设f,g,S和T是模糊度量空间(X,M,*)中的4个自映象,且满足以下条件：

(i) (f,S)和(g,T)是(Ag)型R-弱交换非相容映象对;

(iii)M(fx,gy,t)≥M(Sx,Ty,φ(t)), ∀x,y∈X,t>0,其中φ满足条件(Φ).

则f,g,S和T有唯一的公共不动点.

证因为(f,S)和(g,T)是非相容映象对,则存在序列{xn},{yn}⊂X,使得

t1=Tu,t2=Sv.

假设Tu≠Sv,根据条件(iii)知

M(fxn,gyn,t)≥M(Sxn,Tyn,φ(t)).

令n→∞,有M(Tu,Sv,t)≥M(Tu,Sv,φ(t)),重复利用该不等式,我们有

M(Tu,Sv,t)≥M(Tu,Sv,φ(t))≥…≥M(Tu,Sv,φm(t)).

其中m∈N+.令m→∞,则M(Tu,Sv,t)≥1,推出矛盾,故Tu=Sv.

若fv≠Sv,根据条件(iii),有M(fv,gyn,t)≥M(Sv,Tyn,φ(t)).

令n→∞,则有M(fv,Sv,t)≥M(Sv,Sv,φ(t))=1,推出矛盾,所以

fv=Sv

(1)

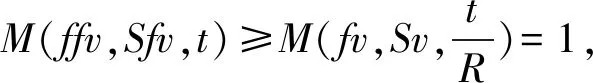
ffv=Sfv

(2)

下证ffv=fv,在条件(iii)中,令x=fv,y=yn,得到

M(ffv,gyn,t)≥M(Sfv,Tyn,φ(t))=M(ffv,Tyn,φ(t))

令n→∞,则得M(ffv,Sv,t)≥M(Sfv,Sv,φ(t)),重复利用此式,可得

M(ffv,Sv,t)≥M(ffv,Sv,φ(t))≥…≥M(ffv,Sv,φm(t))

当m→∞时,M(ffv,Sv,t)≥1.推出矛盾,故

ffv=Sv=fv

(3)

利用式(1),(2)和(3),得到ffv=Sfv=Sv=fv.即fv是f和S的公共不动点.再由条件(iii)和Tu=Sv,可得

M(fv,gu,t)≥M(Sv,Tu,φ(t))=M(Sv,Sv,φ(t))=1

即M(fv,gu,t)≥1.推出矛盾,故fv=gu.

在条件(iii)中,令x=v,y=gu,我们有

M(fv,ggu,t)=M(Sv,Tgu,t)≥M(Sv,Tgu,φ(t)).

重复利用上式,有

M(Sv,Tgu,t)≥M(Sv,Tgu,φ(t))≥...≥M(Sv,Tgu,φm(t)).

令m→∞,此时M(Sv,Tgu,t)≥1,推出矛盾.故Sv=Tgu.

综上,Sv=fv=Tgu=ggu=gu,所以Tgu=ggu=gu.即gu是T和g的公共不动点.

令w=fv=gu,则w是f,g,S和T的公共不动点.

下证不动点是唯一的,令w′是f,g,S和T的另一个公共不动点.

根据条件(iii),我们有M=(w,w′,t)=M(fw,gw′,t)≥M(Sw,Tw′,φ(t))=M(w,w′,φ(t)),即

M=(w,w′,t)=M(w,w′,φ(t))

重复利用上式,得到

M=(w,w′,t)≥M(w,w′,φ(t))≥…≥M(w,w′,φm(t))

令m→∞,此时M=(w,w′,t)≥1,推出矛盾,所以w=w′,唯一性得证.

推论1令f,g是模糊度量空间(X,M,*)上的(Ag)型R-弱交换非相容映象对.若满足

M(fx,gy,t)≥M(x,y,φ(t))

其中t>0, ∀x,y∈X,φ满足条件(Φ),则f和g在X中有唯一的公共不动点.

证只需在定理1中取S=T=I即可.

推论2令f是模糊度量空间(X,M,*)上的自映象,且满足下列条件

M(fx,fy,t)≥M(x,y,φ(t))

其中t>0, ∀x,y∈X,φ满足条件(Φ),则f在X有唯一的不动点.

证在定理1中取S=T=I,f=g即可.

推论3令f和S是模糊度量空间(X,M,*)上的自映象对,且满足下列条件:

(i) (f,S)是(Ag)型R-弱交换的非相容映象对;

(iii)M(fx,fy,t)≥M(Sx,Sy,φ(t)),

其中t>0,∀x,y∈X,φ满足条件(Φ).则f和S在X中有唯一的公共不动点.

证在定理1中取S=T,f=g即可证明.

定理2设(X,M,*)是模糊度量空间,S,T,fi(i∈I),分别是X上的自映象和自映象族,其中I是指标集,I的势不小于2,同时满足以下条件：

(i) ∀i∈I, (fi,S)和(fi,T)是(Ag)型R-弱交换非相容映象对;

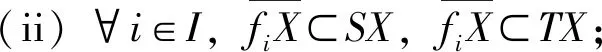
(iii) ∀x,y∈X,M(fix,fiy,t)≥M(Sx,Ty,φ(t)),

其中i,j∈I(i≠j),t>0,φ满足条件(Φ).则S,T,fi,i∈I在X中有唯一的公共不动点.

证∀i,j,m∈I,其中i≠j,i≠m,由定理1知,S,T,fi,fj和S,T,fi,fm分别在X中有唯一的公共不动点xij,xim,根据条件(iii)可知,

M(fixij,fmxim,t)≥M(Sxij,Txim,φ(t)).

即M(xij,xim,t)≥M(xij,xim,φ(t)),重复利用此式可得

M(xij,xim,t)≥M(xij,xim,φ(t)≥…≥M(xij,xim,φn(t)).

令n→∞,根据引理2,有xij=xim,又因为i,j,m是任意的,从而S,T,fi,i∈I在X中有唯一的公共不动点.

定理3设(f,S),(g,T)是模糊度量空间(X,M,*)上的两对(Ag)型R-弱交换非相容映象对,且满足以下条件：

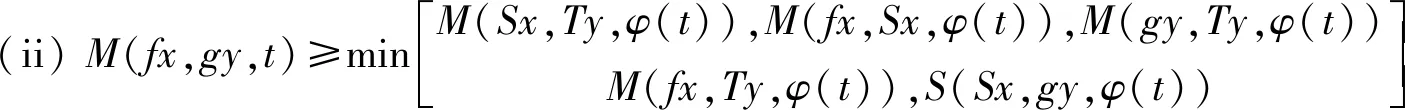
∀x,y∈X,t>0,其中φ满足条件(Φ),则f,g,S和T有唯一的公共不动点.

证因为(f,S)和(g,T)是X上的非相容映象对,则存在序列{xn},{yn}⊂X,使得

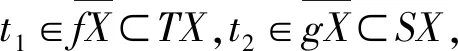
t1=Tu,t2=Sv.

由条件(ii)知,

令n→∞,则

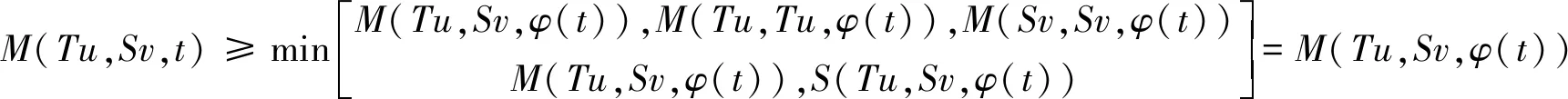
即M(Tu,Sv,t)≥M(Tu,Sv,φ(t)).重复利用此式,有

M(Tu,Sv,t)≥M(Tu,Sv,φ(t))≥…≥M(Tu,Sv,φm(t)),m∈N+

令m→∞,则得M(Tu,Sv,t)≥1,推出矛盾,故Tu=Sv.

在条件(ii)中,令x=v,y=yn,

不等式两边令n→∞,得到

多次利用上述不等式,有M(fv,Sv,t)≥M(fv,Sv,φ(t))≥…≥M(fv,Sv,φm(t)).令m→∞,则得M(fv,Sv,t)≥1.推出矛盾,故fv=Sv.

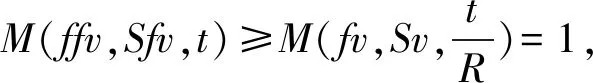
不等式两边令n→∞,则

同理,我们得到M(ffv,Sv,t)≥1,推出矛盾.故ffv=Sv=fv.综上,ffv=Sfv=Sv=fv,即fv是f和S的公共不动点.

根据条件(ii)和Tu=Sv,那么

因此Tu=Sv=fv=gu,所以Tu=gu.

再次利用条件(ii),得到

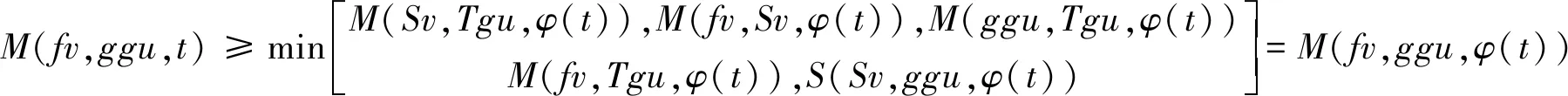
同理可得M(fv,ggu,t)≥M(fv,ggu,φ(t))≥…≥M(fv,ggu,φm(t)).在上式中令m→∞,M(fv,ggu,t)≥1.推出矛盾,故fv=ggu.综上,Sv=fv=Tgu=ggu=gu,所以Tgu=ggu=gu,即gu是T和g的公共不动点.

令z=fv=gu,则z是f,g,S和T的公共不动点 .最后证明不动点是唯一性的,令z′是f,g,S和T的另一个公共不动点.根据条件(ii),我们重复利用上式,得到

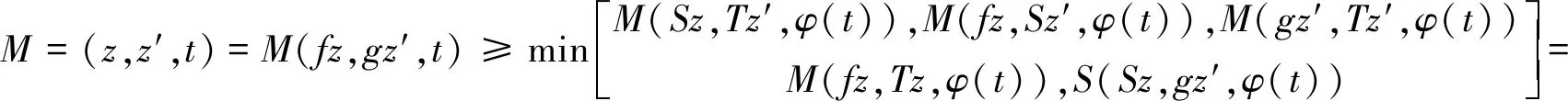
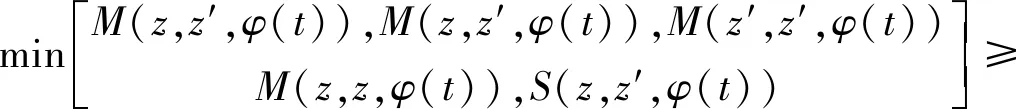
M(z,z′,φ(t))

即M=(z,z′,t)≥M=(z,z′,φ(t)),重复利用此式,我们得到

M=(z,z′,t)≥M(z,z′,φ(t))≥…≥M(z,z′,φm(t))

其中m∈N+.令m→∞,此时M=(z,z′,t)≥1,推出矛盾,所以z=z′,唯一性得证.

注2在定理3中,

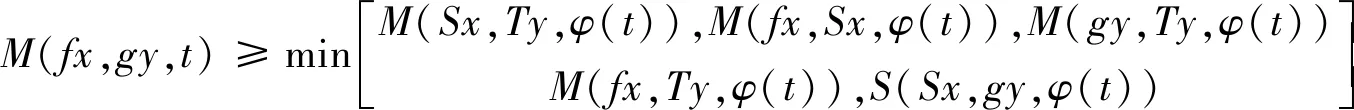
若不等式右端仅含M(Sx,Ty,φ(t)),我们便可得到定理1的结果.

注3在定理3中,分别令S=T=I;S=T=I,f=g,或者S=T,f=g都会得到不同的新结果.

我们记Ψ是所有连续并且递增函数ψ的全体,其中ψ:[0,1]5→[0,1],并且所有的t∈[0,1]满足ψ(t,1,1,t,t)>t,ψ(1,t,1,t,1)>t,ψ(1,1,t,1,t)>t.下面给出几个函数ψ∈Ψ的例子：

(1)ψ(x1,x2,x3,x4,x5)=(min{xi})h, 0

(2)ψ(x1,x2,x3,x4,x5)=(x1)h, 0

我们利用函数ψ的性质,在模糊度量空间中证明以下定理：

定理4设(f,S), (g,T)是模糊度量空间(X,M,*)上的两对(Ag)型R-弱交换非相容映象对,且满足以下条件：

∀x,y∈X,t>0,其中φ满足条件(Φ).则f,g,S和T有唯一的公共不动点.

证因为(f,S)和(g,T)是X上的非相容映象对,故存在序列{xn},{yn}⊂X,使得

t1=Tu,t2=Sv.

由条件(ii)知,

令n→∞,我们有

即M(Tu,Sv,t)≥M(Tu,Sv,φ(t)).重复利用此式,得到

M(Tu,Sv,t)≥M(Tu,Sv,φ(t))≥…≥M(Tu,Sv,φm(t)),m∈N+

在上式中令m→∞,M(Tu,Sv,t)≥1,推出矛盾,Tu=Sv.在条件(ii)中,令x=v,y=yn,

不等式两边令n→∞,可得

多次利用此式,有M(fv,Sv,t)≥M(fv,Sv,φ(t))≥…≥M(fv,Sv,φm(t)) 当m→∞时,有M(fv,Sv,t)≥1.推出矛盾,故fv=Sv.

下证ffv=fv,在条件(ii)中,令x=fv,y=yn,得到

不等式两边令n→∞,我们有

同理,我们得到M(ffv,Sv,t)≥1,推出矛盾.故ffv=Sv=fv.综上所述,ffv=Sfv=Sv=fv,即fv是f和S的公共不动点.

根据条件(ii)和Tu=Sv,那么

因此Tu=Sv=fv=gu,所以Tu=gu.

再次利用条件(ii),令x=v,y=gu

同理可得M(fv,ggu,t)≥M(fv,ggu,φ(t))≥…≥M(fv,ggu,φm(t)).当m→∞时,M(fv,ggu,t)≥1.推出矛盾,故fv=ggu.综上,Sv=fv=Tgu=ggu=gu,所以Tgu=ggu=gu,即gu是T和g的公共不动点.

令z=fv=gu,则z是f,g,S和T的公共不动点.下面证明不动点是唯一的,令z′是f,g,S和T的另一个公共不动点.根据条件(ii),我们有

M(z,z′,φ(t))

即M=(z,z′,t)≥M=(z,z′,φ(t)),重复利用此式,我们得到

M=(z,z′,t)≥M(z,z′,φ(t))≥...≥M(z,z′,φm(t))

其中m∈N+.当m→∞时,M=(z,z′,t)≥1,推出矛盾,所以z=z′,唯一性得证.

注4在定理4中,分别令f,g,S和T中任意两个映象相等或任意多个为恒等映射,都会得到不同的新结果.

本文主要在模糊度量空间中借助(Ag)型R-弱交换的概念,通过引入引理2,在此基础上证明了一些新的压缩映象下非相容映象对的公共不动点定理,得到的结果进一步推广了度量空间、广义度量空间以及概率度量空间中的许多结果.