质量放大系数对冷滚打成形廓形与变形力的影响

梁小明， 吴神丽， 刘 凌， 姚梓萌， 焦艳梅， 柏 朗

(1.西安文理学院 机械与材料工程学院， 西安 710065； 2.陕西省表面工程与再制造重点实验室， 西安 710065)

0 引 言

冷滚打成形是一种无模无约束、加工柔性好的逐渐累积的绿色、近净塑性成形技术，但成形过程涉及多场耦合作用，使金属塑性流动的行为产生多样性，形状尺寸及质量的控制更加困难，严重制约了该项成形技术的实际应用。有限元技术的出现，为研究冷滚打成形这一复杂过程提供了有效的手段。崔克天等[1]最早在花键冷滚打成形中应用了有限元技术，研究了成形过程中塌陷缺陷产生的原因。全建辉等[2]指出了冷滚打成形花键仿真时存在的问题，分析其成形过程。李言等[3-7]利用ABAQUS软件建立了冷滚打板料、齿条的有限元模型，模拟得到了成形力大小和应力场、应变场的分布规律，通过实验验证，揭示了高速冷滚打成形时的应力、应变、温度、金属流动变化规律。崔凤奎等[8-11]运用ABAQUS仿真软件对冷滚打成形过程进行建模仿真，分析了高速精密冷滚打成形过程中的金属流动特性，及其对齿形误差成形尺寸等的影响规律，揭示了冷滚打成形过程中金属材料流动规律和齿形的成形机理。

有限元仿真已成为冷滚打成形技术研究的主要方法[12-13]，如何恰当地运用质量放大系数设置，在满足精度要求的情况下有效缩短计算时间，已是有限元仿真在冷滚打成形技术研究中能否进一步应用的关键所在。笔者依据冷滚打成形的基本原理建立有限元仿真模型，分析质量放大系数与成形精度和效率之间的关系，通过改变质量放大系数研究变形力和齿形轮廓的变化规律，确定出冷滚打成形时比较科学、合理的质量放大系数设置。在自行研发的冷滚打机床上进行实验，验证仿真结果，为冷滚打成形技术有限元仿真过程中精度与效率之间平衡问题的解决提供了重要依据。

1 冷滚打成形与质量放大系数

1.1 冷滚打成形

冷滚打成形技术是利用金属在常温状态下具有一定塑性变形的能力，通过偏心安装在滚打轴上的具有一定形状的滚打轮高速击打工件，随着其相对位置的改变，逐渐累积形成与滚打轮形状啮合的齿形，具体原理如图1所示。

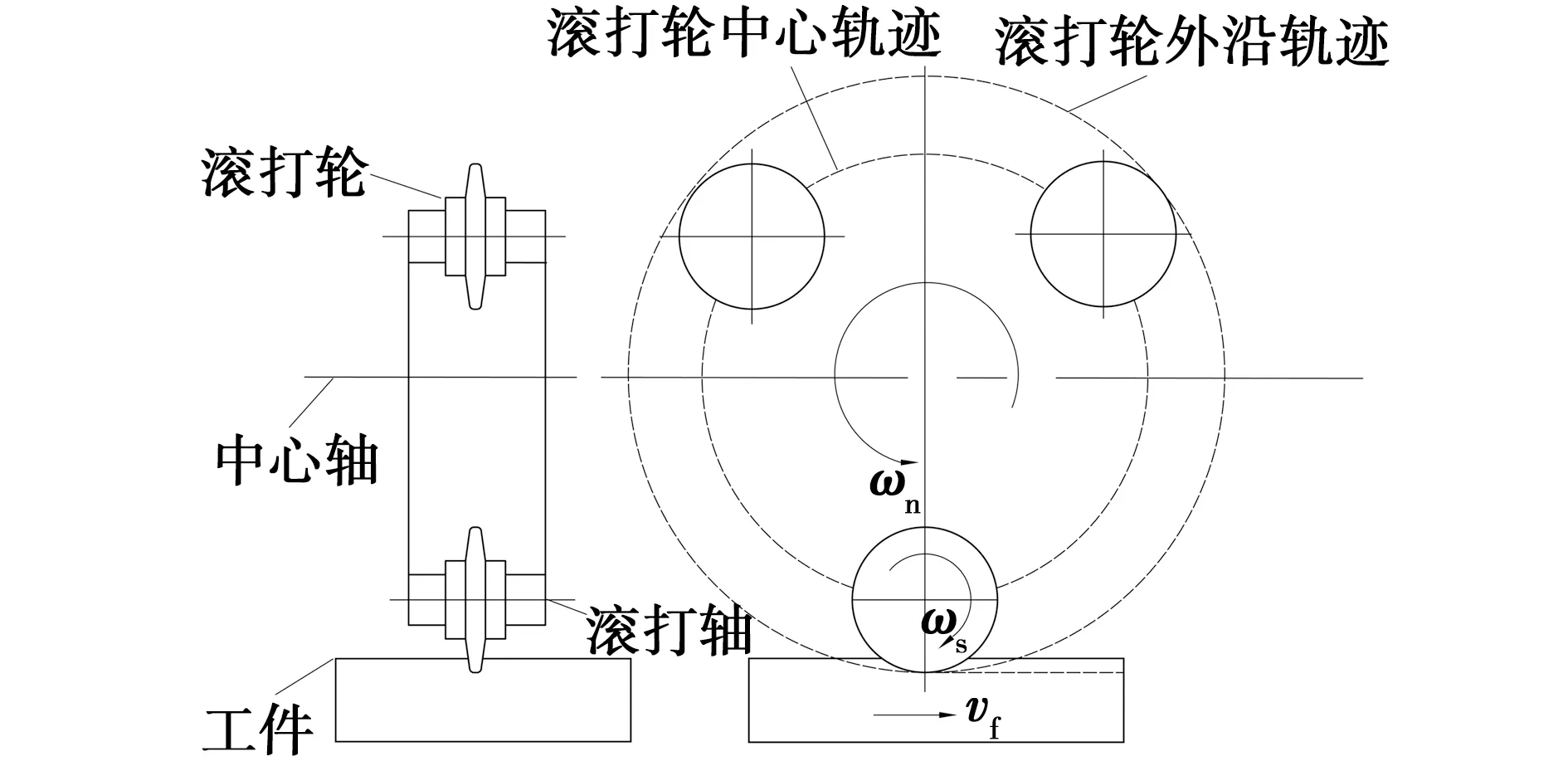
图1 冷滚打成形示意

1.2 质量放大系数

冷滚打成形为了获得比较精确的成形廓形、比较高的表面质量，工件变形部分的网格单元有时特别小，使显式动态分析采用很小的时间步长。由于收敛的问题，时间步长应该小于等于临界时间步长

(1)

式中:Lmin——模型极小单元格的最小长度，mm；

E——杨氏模量，Pa；

ρ——材料密度，g/mm3；

μ——泊松比。

同时，进行计算时需要处理的最小增量数为

(2)

式中，ts——冷滚打成形的实际时间。

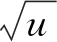
2 有限元仿真

2.1 动态模型的建立

2.1.1 几何模型

为了缩短计算时间，提高计算效率，将成形模型中的轴(滚打轴和中心轴)及支撑机构进行适当简化，建立的模型如图2所示。其中，滚打轮模型主要参数分别为齿顶高2 m、齿根高2.5 m、齿距6.28 m、过渡圆弧半径0.7 m、模数2 m；工件尺寸为22 m×16 m×8 m；装配尺寸分别为滚打半径73 m、滚打深度0.3 m。

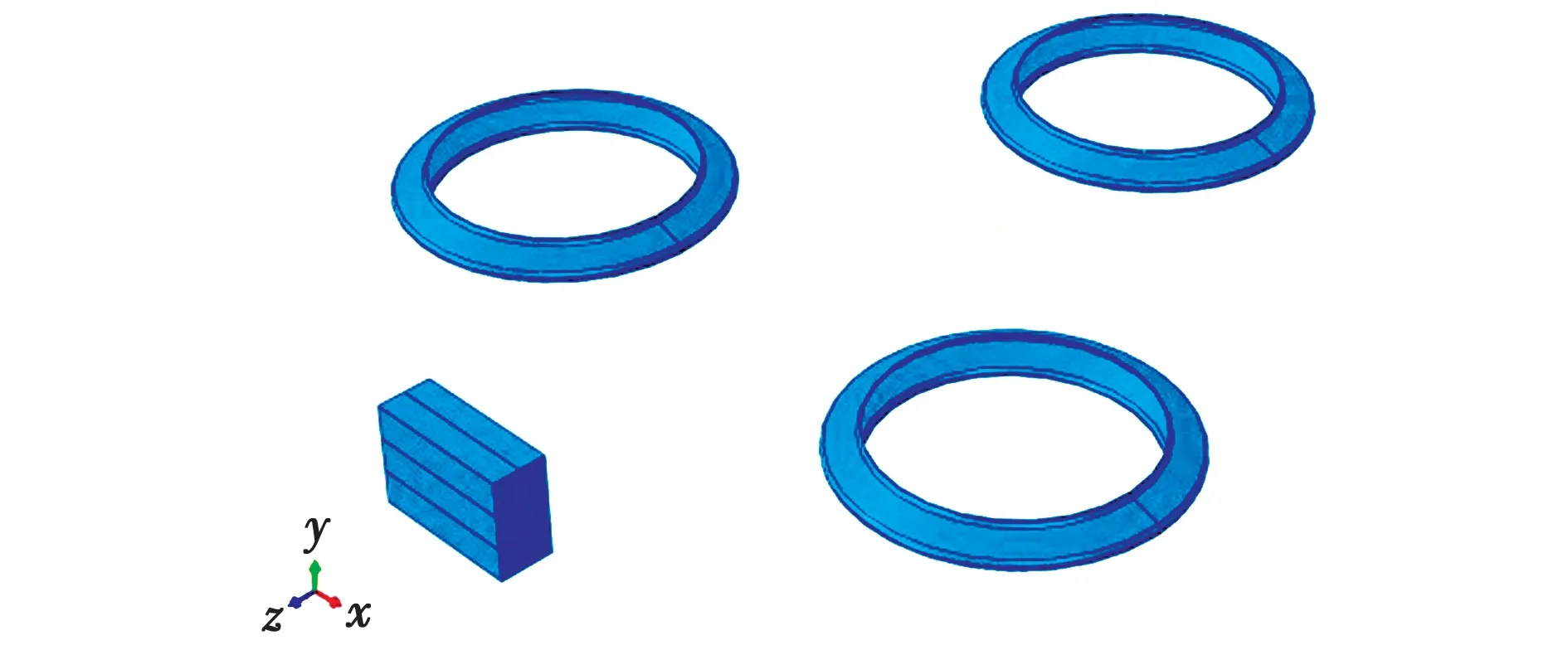
图2 冷滚打有限元模型

2.1.2 材料属性

将滚打轮设置为刚体，设置滚打轮与工件质量同数量级以减小仿真误差，选用适用于金属高应变率变形的J-C模型，成形件材料选用紫铜，其参数如表1所示。其中,σ为屈服应力，B为应变硬化系数，MPa，C为应变率强化系数，n为应变硬化指数，m为温度敏感系数，θ为实验温度，θm为试样熔点，θr为参考温度，℃。滚打轮模型设置为解析刚体。

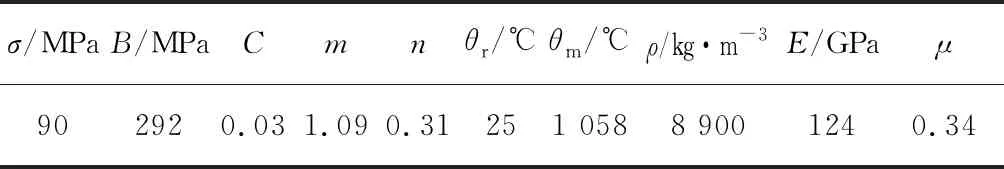
表1 紫铜J-C模型参数

2.1.3 单元选择与网格划分

成形件形状比较规则，网格单元类型选择C3D8R；将工件与滚打轮接触部分的网格进行细化，网格单元的边长为0.1 mm，网格划分后工件如3所示。

图3 工件区域网格划分

2.1.4 相互作用与边界条件设置

设定顺打方式下，滚打轮以1 180 r/min的速度绕y轴旋转，约束其他自由度；工件以60 mm/min水平进给，约束其他自由度，滚打深度设置为 0.3 mm。

2.2 仿真结果与分析

2.2.1 分析路径的选取与区域划分

质量放大系数变化时，为了有效分析成形件廓形随之变化规律，可以过成形件中心点沿y方向取路径，如图4a所示。通过有限元仿真可以获得工件路径上的变形量和截面廓形，将其划分为4个区域：Ⅰ齿槽底部区域，Ⅱ齿槽倒角区域，Ⅲ齿壁区域，Ⅳ齿顶区域，如图4b所示。

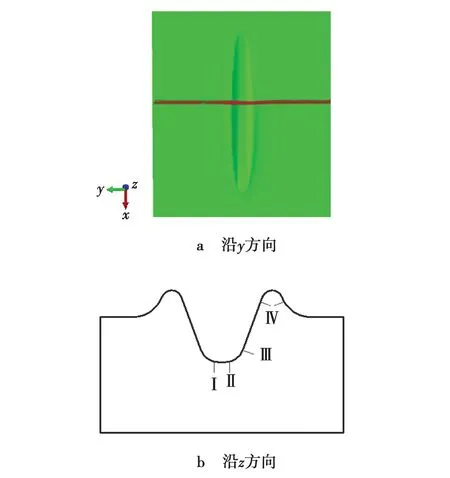
图4 路径的选取

2.2.2 质量放大系数对应力的影响

选取质量放大系数设置为102、103、104、105、106，其他材料参数不变，对紫铜工件进行滚打仿真计算，单次滚打获得成形齿槽及mises应力如图5所示，应力最大处均在齿槽底部倒角处，且随质量放大系数的增大，mises应力最大值也增大；质量放大系数从102增大到105时，mises应力最大值从3.277×108Pa增大到4.019×108MPa；但当质量放大系数从105增大到106时，mises应力最大值从4.019×108MPa突增到5.704×108MPa，从图5e可以看出，其变形过大，与实际情况相差甚远，严重影响了仿真结果，质量放大系数设置不能超过105。

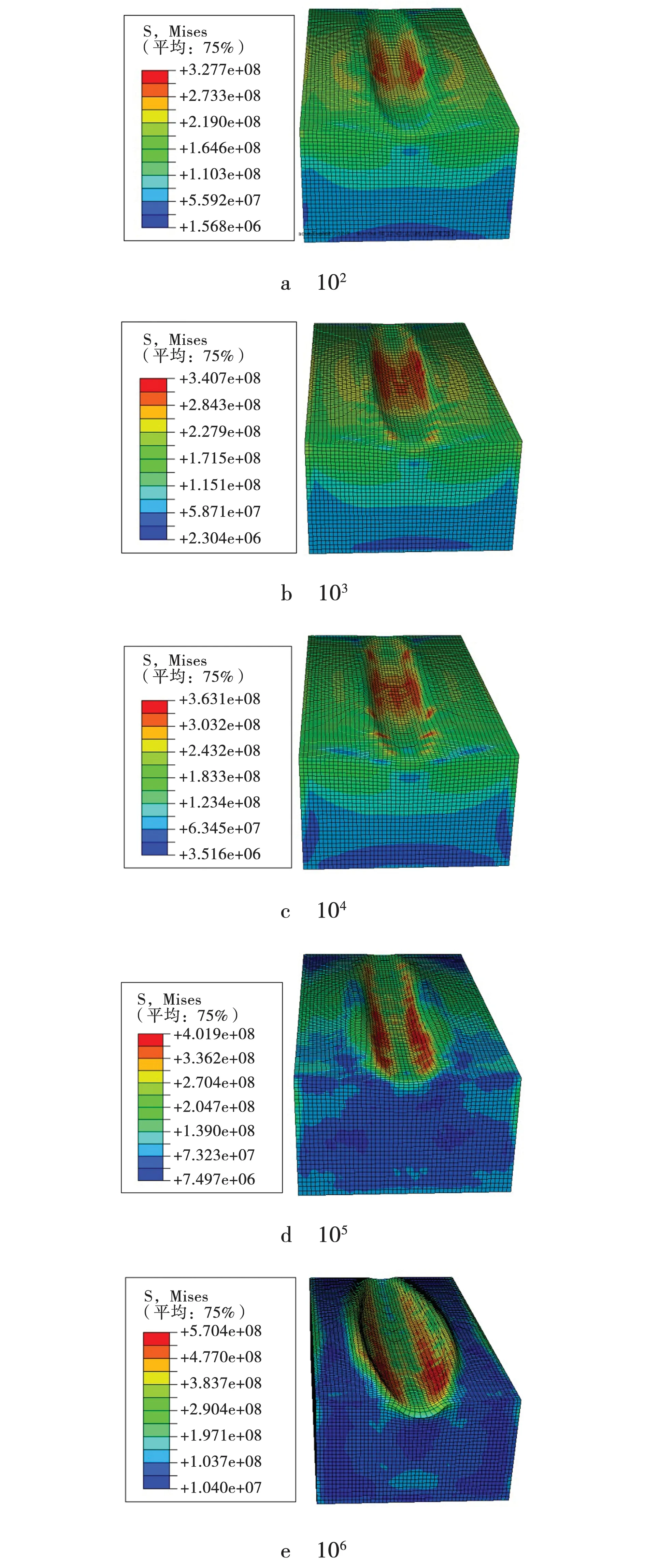
图5 不同质量放大系数时的mises应力图

2.2.3 质量放大系数对成形廓形的影响

(1)同样在冷滚打成形仿真过程中，取质量放大系数为102～106，获得不同质量放大系数时的廓形曲线如图6所示，当质量放大系数为102、103、104时廓形基本相近，且与滚打轮截面形状相似；质量放大系数为105时，齿顶区域稍有差异；当质量放大系数为106时，成形廓形远远大于滚打轮截面形状，且与质量放大系数为102、103、104和105时成形的廓形也相差很大。在进行冷滚打成形廓形仿真时，质量放大系数不能超过105。

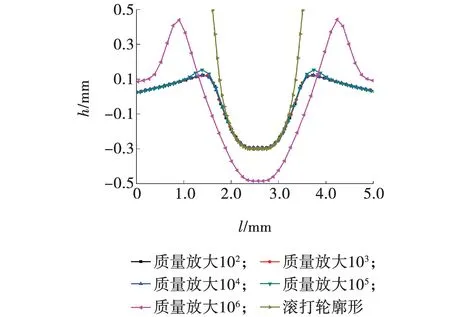
图6 不同质量放大系数成形齿形截面

2.2.4 质量放大系数对变形力的影响

不同质量放大系数时切向和径向单次变形力如图7所示。

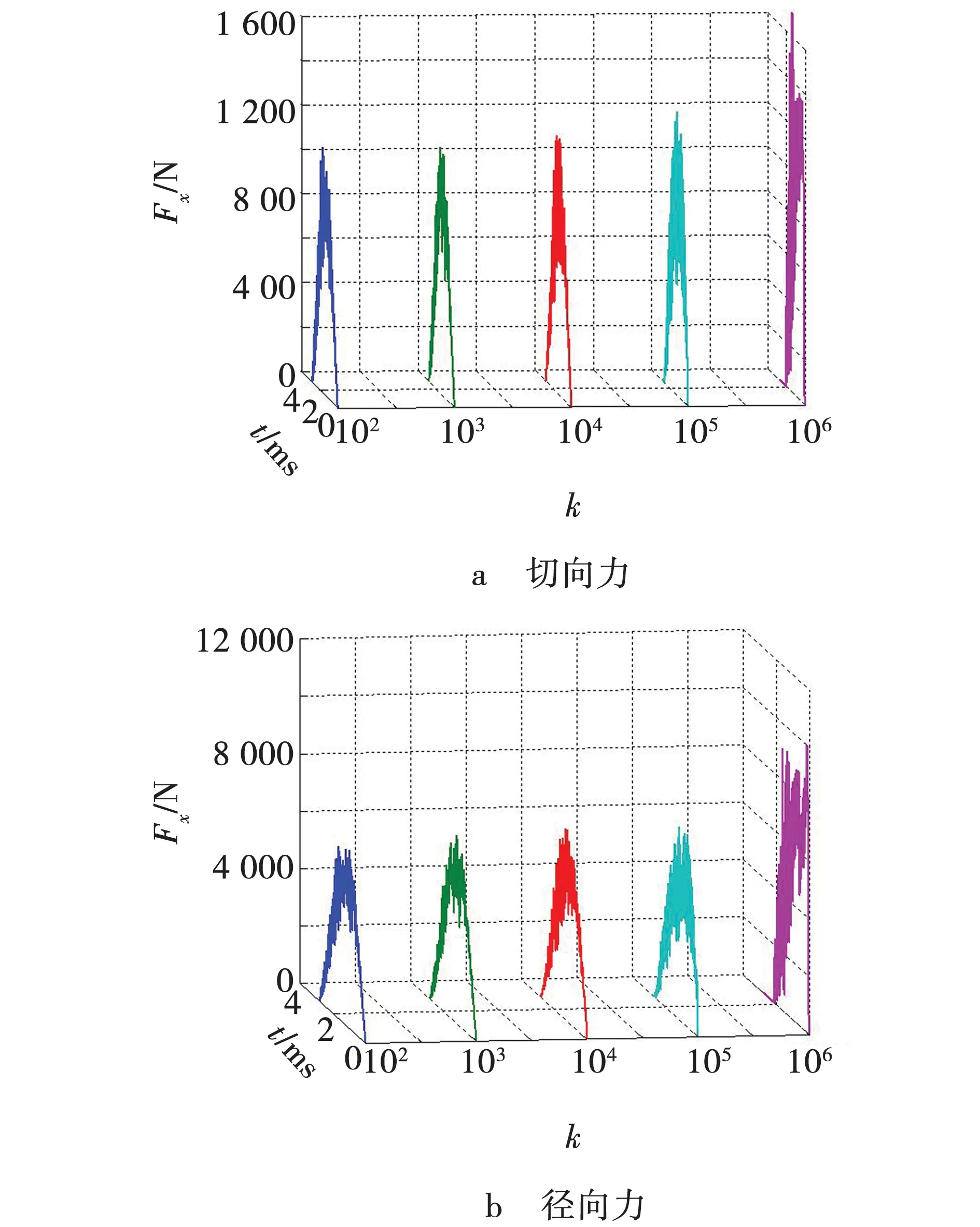
图7 不同质量放大系数时的变形力

放大系数在102～105之间径向力和切向力的变化不大，但当放大系数为106时，两个方向的变形力都出现了突变，说明有限元仿真冷滚打成形力时，质量放大系数在102～105时对变形力的影响不大，在进行冷滚打变形力仿真时，质量放大系数不能超过105。

2.2.5 质量放大系数对计算时间的影响

质量放大系数与计算时间的关系如图8所示。当质量放大系数小于104时，质量增大耗时急剧减小；当质量放大系数大于104时，对冷滚打成形计算时间的影响不太明显，但是对成形廓形和变形力还存在一定的影响。为了保证计算精度，缩短计算时间，综上分析，冷滚打成形有限元仿真时的质量放大系数设置为104比较合理。

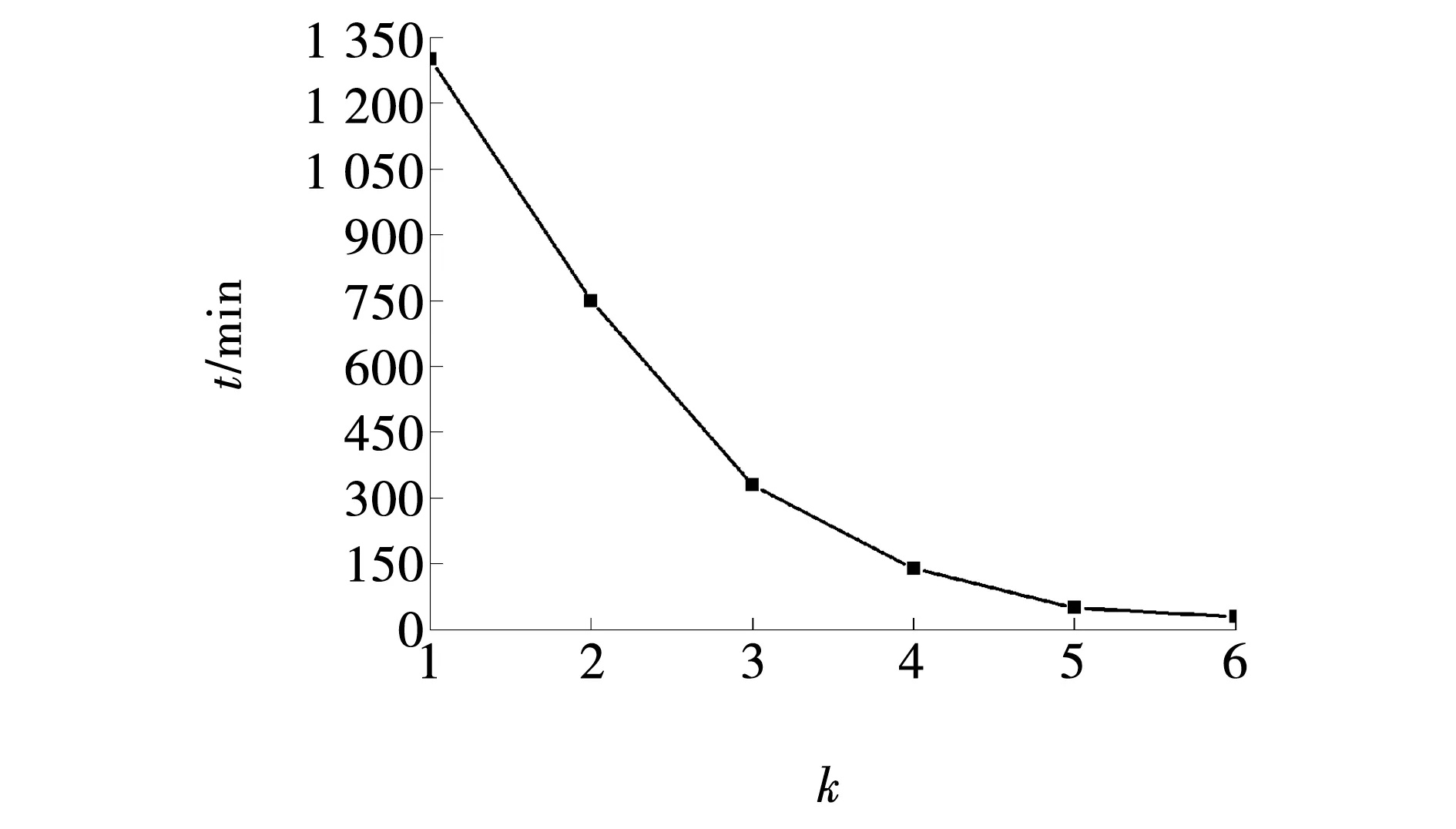
图8 不同质量放大系数下计算耗时

3 实 验

实验在卧式铣床改造成的冷滚打成形设备上进行，铣刀为专用冷滚打装置(图9)，沿着支撑轴圆周方向均匀分布3个用于放置滚打轮的槽。选圆柱滚子组合轴承对滚打轮与芯轴进行装配。组合轴承一端通过滚打轮的端面定位，另外一端通过垫片进行定位，芯轴通过螺栓固定在支撑轴上，整个滚打装置通过主轴安装在卧式铣床上，主轴高速旋转带动滚打装置旋转从而实现工件的冷滚打。滚打轮绕中心轴的速度为1 180 r/min，工件以60 mm/min水平进给，滚打深度设置为0.3 mm，实验参数与仿真参数一致。

通过超景深三维显微系统对截面形状进行测量，测量成形的三维廓形截面如图10a所示，仿真获得齿形区域三维廓形截面如图10b所示。为了将实验获得廓形与仿真和滚打轮截面进行有效比较，需要对测量的廓形截面数据进行奇偶数筛选，然后与仿真结果和滚打轮廓形进行比较，如图11所示。

图9 冷滚打滚打头装置

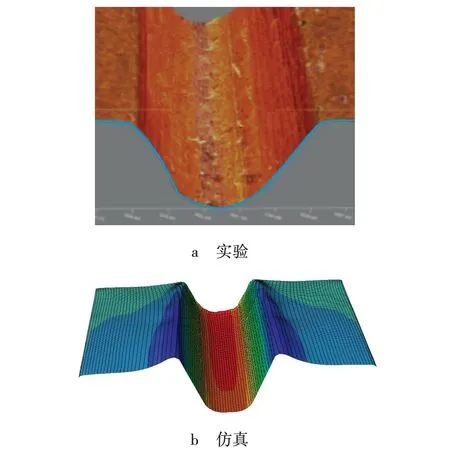
图10 齿槽廓形和截面

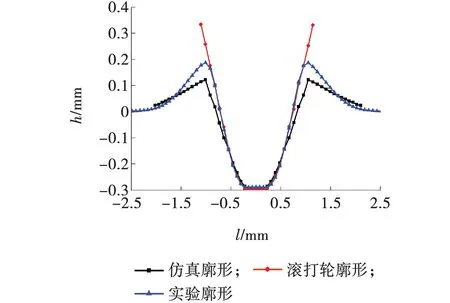
图11 仿真和实验的廓形截面的比较

实验所得廓形截面与仿真以及滚打轮廓形截面很接近，实验所得的廓形与滚打轮截面形状啮合的更好，这是因为仿真过程中网格的划分不够精细、滚打过程中材料的应变率与实验中材料的应变率设置不够准确造成，但在齿底和下半部分齿壁处，仿真和实验与滚打轮截面基本吻合。

在成形实验中，在工件的底部安装专用八角环测力仪(使用前进行了静态标定)，测量冷滚打过程中的变形力，获得径向和切向的滚打力如图12所示。

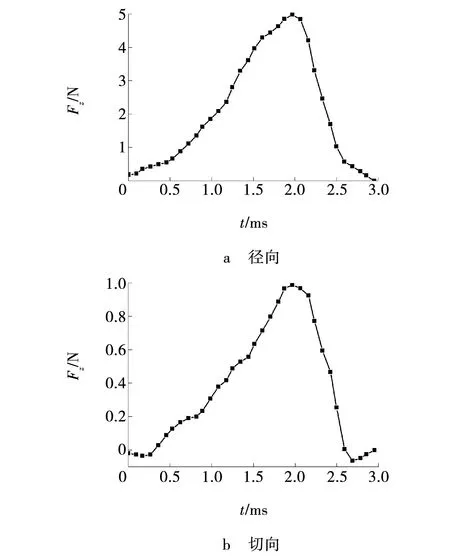
图12 变形力

由图12可见，径向变形力最大值约为5.00 kN，切向变形力最大值约为1.00 kN。质量放大系数设置为104时仿真获得的径向变形力最大值约为4.9 kN，仿真时由于数据采集频率的影响，取最大值及附近的6个点计算平均值，切向变形力的最大值约为1.08 kN(仿真时由于数据采集频率的影响，取最大值及附近的6个点算平均值)。实验与仿真结果径向力最大值相差约2%，切向力最大值相差约为8%，仿真结果与实验结果很接近，说明了仿真模型的正确和质量放大系数设置的合理。

4 结 论

(1)建立了冷滚打有限元仿真模型，得到了成形中质量放大系数对成形廓形和变形力的影响规律。当质量放大系数大于105时，获得的仿真廓形和变形力发生突变，产生误差很大；当质量放大系数系大于104时，计算时间没有明显缩短，且对仿真精度有一定的影响，综合考虑最后选择质量放大系数设置为104。

(2)在改造的冷滚打设备上进行实验，获得了成形过程中的变形力与廓形，与仿真结果基本吻合，说明质量放大系数设置为104比较合理，研究结果可为有限元仿真在冷滚打成形技术中进一步的应用提供借鉴。