粒子群优化交叉偶极子声波测井地层各向异性的反演方法
李鹏举, 魏双宝, 田 甜
(1.东北石油大学 地球科学学院, 黑龙江 大庆 163318; 2.东北石油大学 非常规油气成藏与开发省部共建国家重点实验室培育基地, 黑龙江 大庆 163318)
0 引 言
交叉偶极子声波测井作为测量储层不同方向上声波特性的测井方法,自20世纪90年代初出现以来对声波测井技术的发展与应用具有十分重要的意义,利用交叉偶极子测井数据计算各向异性参数也成为了一种重要手段。横波在各向异性地层中传播时会分裂成与质点偏振方向相互垂直的快横波和慢横波,由此可以分析出地层的各向异性。1986年R.M.Alford[1]提出的旋转分析法成功得到了地层的各向异性方位角,但是该方法在处理各向异性较小的地层时会出现多解的情况,多解性是由于两主波阵列分别处理时的速度误差之和可能会大于对应的快横波与慢横波的速度之差。1999年X.M.Tang等[2]提出了波形反演的方法来反演地层的各向异性,该方法能够大大压制或消除波形数据中的噪音影响,但是由于波形反演算法数据量大,反演函数又具有多个极值点,所以快速、准确地求取全局最优解成为了关键。国内学者以波形反演法公式为目标函数提出了一些相关的方法。2001年陶果等[3]利用模拟退火法求解偶极横波时差。2005年何峰江等[4]将改进的模拟退火算法应用于正交偶极子各向异性反演中。2007年王才志等[5]利用极快速模拟退火算法反演地层各向异性。2010年刘宇[6]综合极快速模拟退火法和变区间局部模拟退火法进行各向异性计算,均取得了一些应用效果。
粒子群优化(particle swarm optimizer,PSO)算法是当前研究与应用最广泛的群智能算法之一,由J.Kennedy和C.Eberhart在1995年提出[7]。PSO算法在求解最优化问题,特别是非线性、多峰、不可导等复杂优化问题中具有较强的全局搜索能力,现已成功应用于函数优化、信号处理、神经网络训练、模式分类、数据挖掘等多学科领域。目前,在地球物理测井方面的应用还很少,2014年江沸菠[8]通过将粒子群优化算法与BP神经网络相结合反演非线性电阻率成像,2016年周超[9]对改进的粒子群优化算法识别裂缝属性进行了研究,2018年蔡伟等[10]提出应用粒子群优化算法反演瑞雷波频散曲线。文中提出了将粒子群优化算法应用于提取交叉偶极子声波测井地层各向异性参数的方法,由于充分利用了PSO算法全局寻优、收敛速度快、求解精度高的特点,因此该方法能够得到全局最优解,在各向异性比较弱的地层仍然适用,计算的结果准确可靠。
1 地层各向异性反演原理
1.1 Alford旋转法提取快、慢横波原理
交叉偶极子声波测井采集4个分量的声波阵列数据,如图1所示。单个源距的接收器所测量的4个波形信号分别为
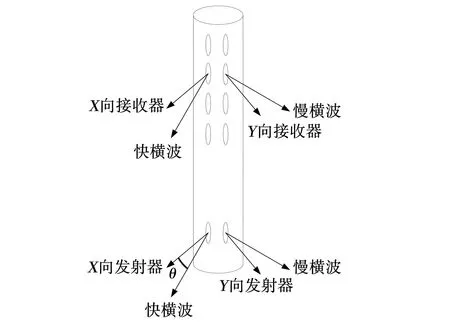
图1 各向异性地层中四分量交叉偶极子测井示意
(1)
式中,Fp(t)和Sp(t)分别代表快、慢横波。把式(1)写成矩阵形,即
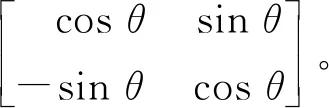
将带有Fp(t)和Sp(t)的矩阵移到等式左边,可以得到
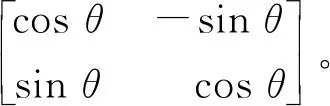
因此,可以得到快、慢横波波形的表达式为
(2)
1.2 反演目标函数的构建
通过上述分析得到了快、慢横波波形表达式。为了增加反演时目标函数对θ角变化的敏感性,对式(2)中的角度θ求导数,得到两个辅助主波表达式为
由于分裂的快、慢横波的极性相同和波形相似,所以可以通过相同和不同接收器间的快、慢横波移动来完成匹配,如图2所示,先把接收器n上的慢横波传播到接收器m的位置,再在时间上向前移动一定时间,来匹配该位置上的快横波。即有
其中,m和n表示第m个和第n个接收器;Δz是相邻两个接收器的间距;Δs为快、慢横波的慢度差;zm是第m个接收器到声源的距离。然后对匹配误差进行累加可得到如下的反演目标函数:
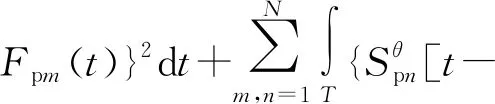
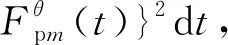
(3)
式中:E——目标函数;
N——接收器的总数;
T——处理的时间宽度;
s2——慢横波的慢度。
当目标函数值达到全局最小时,在处理时窗T内快、慢横波才能得到最佳匹配,此时的θ角为快横波方位角。
反演出Δs、s2和θ以后,就可以得到地层各向异性,其中θ为各向异性方向,各向异性大小按式(4)计算:
(4)
式中:Anis——地层各向异性大小;
s1、s2——快、慢横波的慢度。
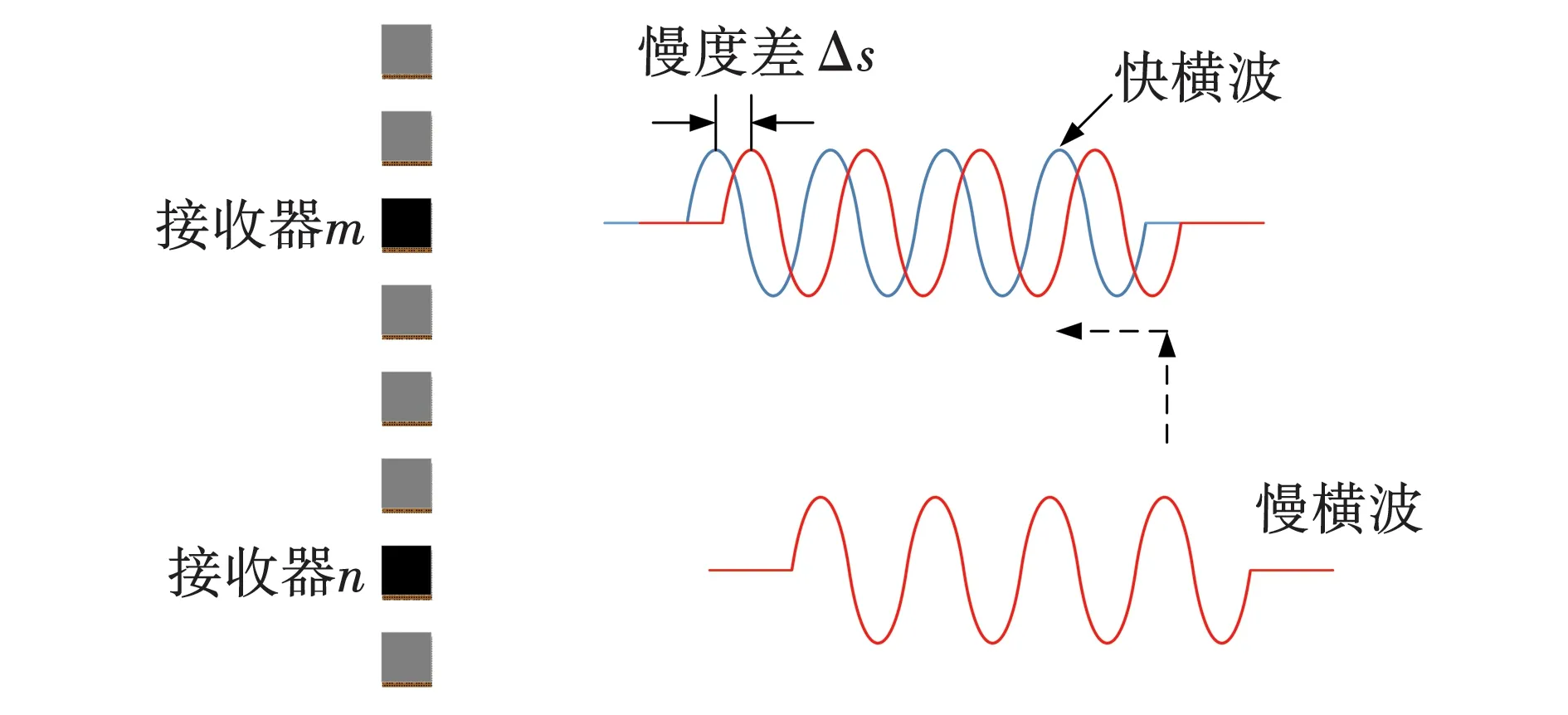
图2 接收器阵列快、慢横波匹配处理示意
2 地层各向异性反演方法
如上所述,地层各向异性反演就是采用一定的优化方法寻找目标函数(3)的最小值。文中提出采用粒子群优化算法对目标函数(3)进行优化求解,同时反演出各向异性的方位与大小。
2.1 粒子群优化算法
粒子群优化算法是一种稳定、适用性强的全局优化算法,它是通过个体间的协作与竞争实现复杂空间中最优解的搜索。PSO算法是在可行解空间中初始化一群粒子,在每一代中粒子通过追随两个极值而动,一个是粒子本身迄今找到的最优解,另一个是种群迄今找到的最优解。其数学描述如下:
设在一个D维的搜索空间中由m个粒子组成的种群,其中第i个粒子位置为xi=(xi1,xi2,…,xiD),其速度为vi=(vi1,vi2,…,viD)。第i个粒子搜索到的最优位置为pi=(pi1,pi2,…,piD)。整个种群搜索到的最优位置为pg=(pg1,pg2,…,pgD)。按追随当前最优粒子的原理,粒子每一维速度和位置都按照式(5)、(6)进行变化:
(5)
(6)
其中,d=1,2,…,D,D为维数;i=1,2,…,m,m为种群规模;t为当前进化代数;r1和r2为分布于[0,1]之间的随机数;c1和c2为加速常数,是粒子向自身极值和全局极值推进的加速权数,文中设置为2。此外,为防止粒子速度过大,可设定速度上限vmax,即当vid>vmax时,取vid=vmax;当vid<-vmax时,取vid=-vmax。粒子群的初始位置和初始速度都是随机产生的,按式(5)和(6)进行迭代,直至两代全局最优位置之差小于给定精度。
为了更好的控制算法的探测和开发能力克服PSO算法在后期搜索速度慢等缺点,Y.Shi等[11]在式(7)的基础上引入了惯性权重w,即速度更新公式变为
(7)
由式(6)和(7)组成的迭代算法为标准粒子群优化算法。惯性权重w表示粒子上一代速度对当前代速度的影响,加强了PSO算法的全局搜索能力。控制w取值大小可调节PSO算法的全局与局部寻优能力。w值较大,全局寻优能力强,局部寻优能力弱;反之,则局部寻优能力增强,而全局寻优能力减弱[12]。针对文中问题,通过试验得出设置w为0.9时,处理效果较好。
2.2 反演方法的具体步骤
(1)数据预处理:对波形数据进行去增益、滤波及均衡化处理。
(2)根据实际地层给定慢横波慢度s2和快慢横波慢度差Δs范围,例如,慢横波慢度s2为131.2~393.6 μs/m、快慢横波慢度差Δs为0~65.6 μs/m,快横波方位角θ为0~180°。
(3)初始化:在给定范围内随机生成初始位置xi=(Δsi,θi,s2i)及其速度vi=(vΔsi,vθi,vs2i),其中i=1,2,…,m,m=50为种群规模。同时将每个个体的初始位置设为当前每个粒子的最优位置pi,把所有粒子的最优位置作为当前整个种群的最优位置pg。
(4)读取某一深度点的8道四分量波形数据,根据每个粒子的位置按照式(3)计算各向异性目标函数E。
(5)评价每一个粒子:如果粒子函数值小于其历史最小值,则将pi设置为该粒子的位置,并更新个体极值。如果所有粒子的个体极值中最小值小于当前的全局极值,则将pg设置为该粒子的位置,并更新全局极值。
(6)粒子的更新:对每一个粒子的速度和位置按照式(6)和(7)进行更新。
(7)检验是否结束:如果当前迭代次数达到了给定的最大迭代次数或两代全局最优位置之差小于给定精度ε,则停止迭代,结束该深度点的计算,输出快横波方位角度、快慢横波慢度及各向异性大小;否则迭代次数t=t+1,转到步骤(5)。
(8)重复步骤(3)到步骤(7),直到整个深度段全部处理完毕。
3 实际测井资料的处理
为进一步验证文中方法的有效性,处理了多口交叉偶极子阵列声波测井(XMAC)资料,其中图3为某井的处理成果,选取2 900~2 950 m深度段。图中第1道为伽马测井曲线和井径曲线;第2道为深度道;第3道是同向分量(XX)的变密度波形;第4道是各向异性大小,其中红色为文中方法计算的各向异性大小,蓝色为CIFLog软件快速模拟退火法计算的各向异性大小;第5、6道分别为两种方法计算的快、慢横波慢度曲线;第7道为两种方法计算的快横波方位角曲线。
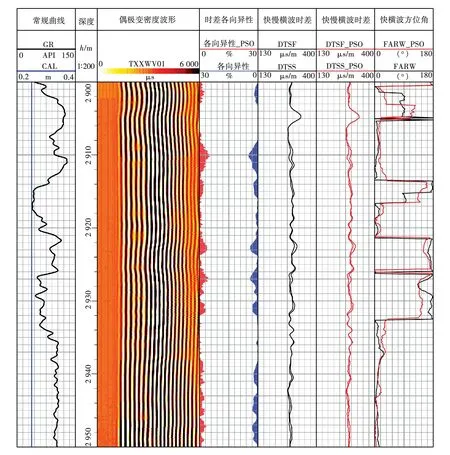
图3 解释成果与各向异性参数对比
从图3中可以看出,在各向异性大小Anis较小,即地层各向异性较弱的位置,相比于快速模拟退火法,文中计算的快横波方位角连续稳定,因此文中方法在弱各向异性地层的计算结果更稳定可靠。在多口井的地层各向异性处理上,文中方法和快速模拟退火法的计算结果基本一致,且文中方法对弱各向异性地层处理的稳定性和计算速度都有所提高,验证了文中方法求解各向异性参数的有效性。
4 结束语
笔者提出并实现了一种利用交叉偶极子声波测井资料反演地层各向异性参数的方法。该方法通过交叉偶极子声波测井四分量数据推导出快、慢横波表达式,将所有接收器的波形进行匹配构建反演目标函数,利用粒子群优化算法求解反演目标函数的最小值,得到各向异性大小及方向。实际测井数据处理结果表明,文中提出的粒子群优化算法反演交叉偶极子声波测井地层各向异性参数的方法是准确、有效、可靠的,并且提高了计算速度及处理结果的稳定性。因此,该方法具有较高的实用价值,为交叉偶极子声波测井数据各向异性反演提供了新的思路和方法。

