基于星点设计的碟盘刀具截割煤岩性能评价与预测
刘春生, 车长瑞
(1.黑龙江科技大学, 哈尔滨 150022; 2.黑龙江科技大学 机械工程学院, 哈尔滨 150022)
0 引 言
煤炭资源是我国能源的重要组成部分,国内外学者对机械法截割煤岩性能做了诸多研究[1]。Goktan等[2]利用岩石截割实验,基于半经验法改进了Evans理论模型,给出了截割力峰值和均值的预测模型。罗鑫等[3]以巷道掘进机截齿的截割性能为研究对象,指出截齿在附加载荷冲击作用下破岩性能得到提高。梁运培等[4]分别运用单因素回归与多因素回归证明Evans理论模型较其他改进模型对截割力有更好的预测。Saurabh等[5]以截割量、齿尖温度、镐齿磨损三因素分析两种镐齿沿直线截割过程中的倾斜角度。刘春生等[6-8]利用ABAQUS软件模拟得到碟盘刀具在不同结构参数下的截割煤岩效果,采用正交数值模拟评价截割煤岩性能。胡琴等[9]应用模糊正交法证明齿形参数对盘式齿破岩效率的影响程度,从大到小依次为顶圆半径、锥角及分屑槽数量。翟强[10]研究了TBM滚刀破岩性能评价指标选取及TBM滚刀截割煤岩性能评价方法。学者采用正交设计、均匀设计以及遗传算法、神经网络等算法进行优选截割煤岩性能参数[11-12]。响应曲面法通过对因素与响应关系进行多项式近似拟合,分析单个因素与响应之间的独立影响和多个因素与响应之间的交互影响,找出最优的因素组合[13]。笔者应用ABAQUS软件数值模拟碟盘刀具截割煤岩,根据进给速度、振动频率、切削厚度应用3因素5水平的星点设计实验方法,建立截割力的多项式回归模型,应用等高线图分析因素间作用,利用熵值法分配权重和多目标综合评价,对比数值模拟、实验与预测模型计算结果,验证回归模型的准确性。
1 星点设计数值模拟方案
1.1 有限元模型的建立
应用ABAQUS软件建立碟盘刀具与煤岩体模型,设置碟盘刀具模型尺寸:碟盘刀具半径为125 mm,楔面角度为55°,刀齿半径为3 mm;煤岩体模型的长宽高分别为420、280、120 mm[14],对碟盘刀具与煤岩体采用六面体C3D8R网格进行划分。
假设碟盘刀具设置为刚体材料,密度ρ1=7 850 kg/m3,弹性模量E1=218 GPa,泊松比μ1=0.28[14]。煤岩体材料选用Drucker-Prager本构模型,其材料属性为:密度ρ2=1 500 kg/m3, 弹性模量E2=1.4 GPa,泊松比μ2=0.3,煤岩体抗压强度σ=30 Mpa,碟盘刀具与煤岩之间采用面对面接触模型和动力显示模型[15]。碟盘刀具与煤岩的网格划分模型,如图1所示。
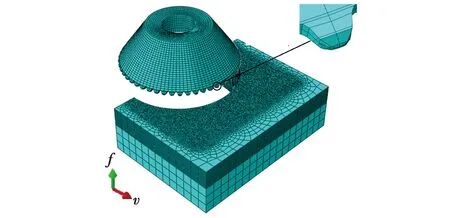
图1 有限元模型
1.2 设计方案
正交设计和均匀设计在进行工艺优化时,虽然有均匀分散、实验次数较少等优点,但是也存在精度不够、预测性差等缺点[17]。星点设计(Central composite design)具有较高精密度、预测值较为接近真实值等优点。为提高碟盘刀具振动切削截割煤岩性能,应用CCD方法设计数值模拟方案,运用星点设计-响应面法分析碟盘刀具振动切削截割煤岩性能的预测。
根据星点实验设计的方案设计3因素5水平的数值模拟,3因素取值范围分别为:进给速度v为300~600 mm/s,切削厚度h为10~30 mm,振动频率f为30~70 Hz。5水平实验用代码值-α、-1、0、1、3因素的星点设计取α=1.732。代码值α、-α为取值范围极值,-1、0、1水平的取值遵循任意两个物理量之间的差值与对应代码之间差值成等比的关系。数值模拟因素代码值所代表的实验参数见表1。
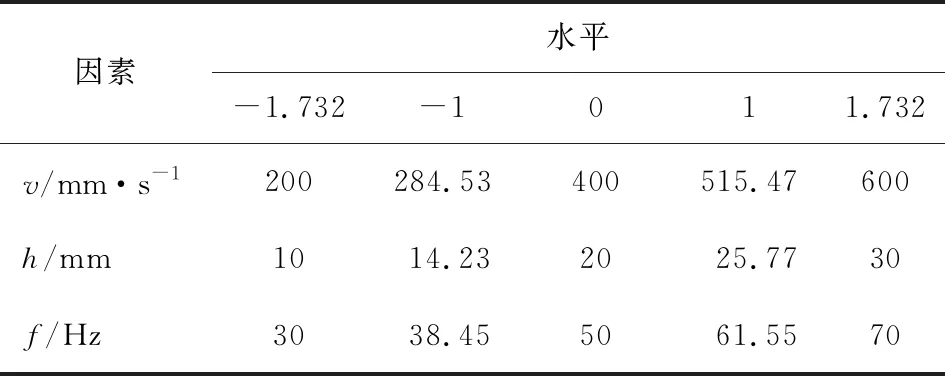
表1 星点设计数值模拟因素水平
根据星点设计实验方案进行15组数值模拟,如表2所示。

表2 星点设计数值模拟方案与结果
图2为数值模拟11、12、15在进给速度v=300 mm/s、振动频率f=50 Hz、切削厚度分别为h=10、30、20 mm参数下的径向载荷Fj、轴向载荷Fz和总载荷Fh的载荷谱。由载荷谱可知,当碟盘刀具振动切削截割煤岩进入稳点段呈周期性变化时,随切削厚度增大,径向载荷峰值均值增大,轴正向载荷峰值均值增大,轴负向载荷峰值均值无明显变化,总载荷峰值均值增大。
采用数值模拟载荷谱的曲线峰值均值和曲线均值来衡量碟盘刀具所受载荷,应用盒维数来间接反映碟盘刀具截割煤岩的比能耗。根据数值模拟载荷谱得到表2中的结果,径向载荷峰值均值F1、轴正向载荷峰值均值F2、轴负向载荷峰值均值F3、总载荷峰值均值F4、总载荷曲线均值F5,总载荷盒维数F6。
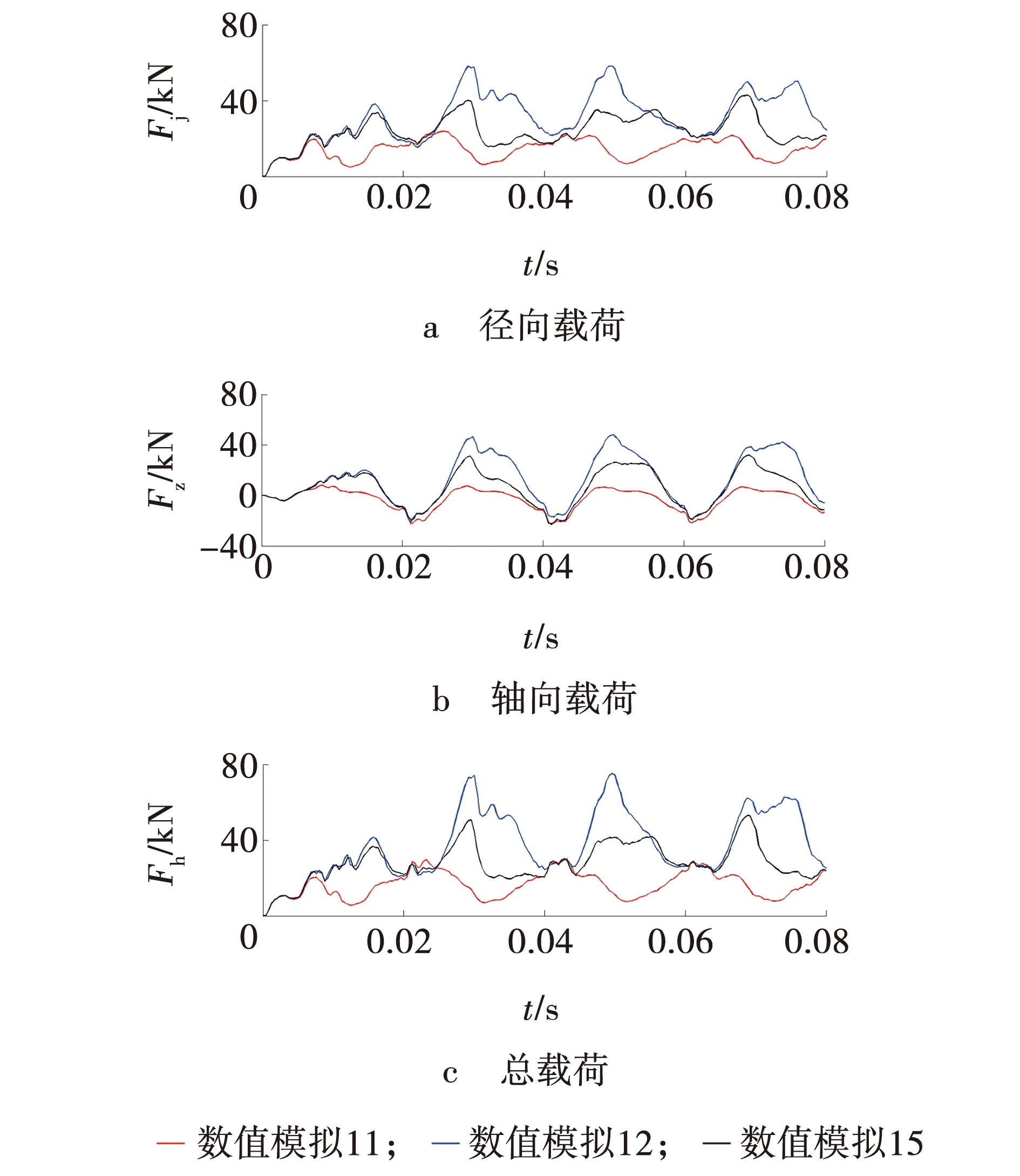
图2 数值模拟11、12、15载荷曲线
图3为碟盘刀具截割煤岩前一时刻径向载荷应力云图,碟盘刀具处于煤岩最大损伤位置,应力由碟盘刀具沿x轴方向先增大后减小、沿y轴方向向两侧逐渐减小。数值模拟11、12、15为进给速度和振动频率相同时,切削厚度分别为10、30、20 mm时的应力状态,可发现煤岩破碎面积与径向载荷峰值均值随切削厚度的增加而增大,径向载荷峰值均值分别为22.469、58.188、41.567 kN。
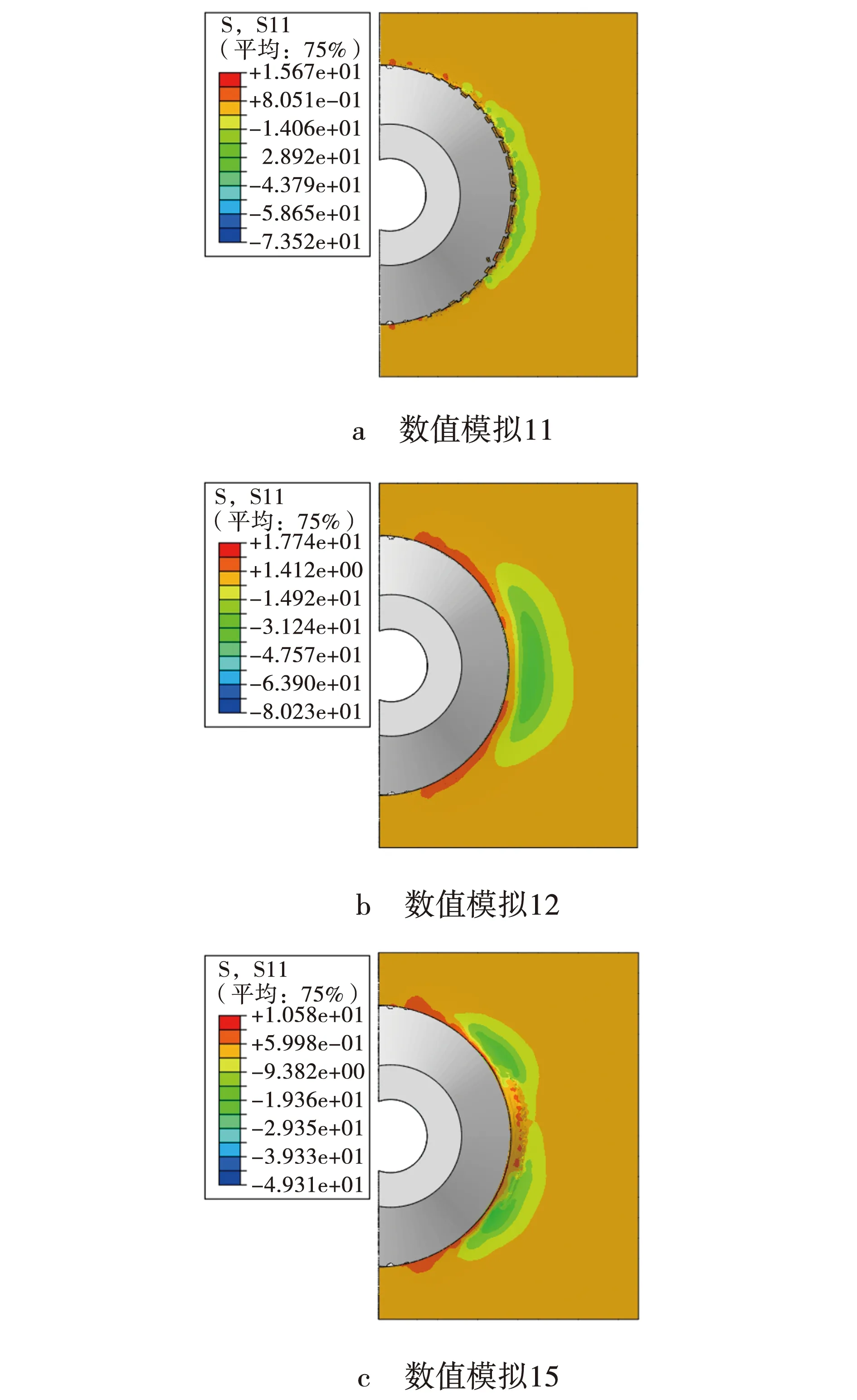
图3 数值模拟11、12、15应力云图
2 回归模型建立与综合评价
2.1 回归模型建立及检验
多因素作用时,考虑因素间的相互作用,建立多项式回归模型为
F=b0+b1X1+b2X2+b3X3+b4X1X2+b5X1X3+b6X2X3,
(1)
式中:bj——回归模型拟合系数,j=0,1,…,6;
Xk——数值模拟实验因素,k=1,2,3。
根据表2中15组数值模拟结果,分别建立各响应Fi的回归模型。回归模型的t检验为
(2)

μ——总体平均数;
σF——样本标准差;
n——样本容量。
一般以P<0.05为有显著统计学差异进行逐步递减回归,得到P值分别为P1≈0.030 4、P2≈0.030 8、P3≈0.000 1、P4≈0.035 8、P5≈0.007 4、P6≈0.005 9。检验后径向载荷峰值均值F1、轴正向载荷峰值均值F2、轴负向载荷峰值均值F3、总载荷峰值均值F4、总载荷曲线均值F5、总载荷盒维数F6的回归模型为
(3)
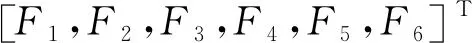


采用确定系数R2判断各响应回归模型拟合的优劣。
(4)
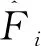
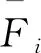
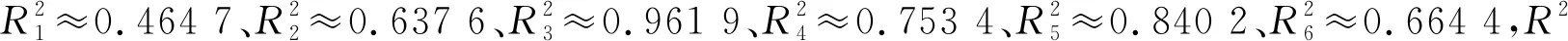
2.2 等高线
为了分析进给速度v、切削厚度h、振动频率f中任意单因素作用或任意两因素同时作用对碟盘刀具所受载荷的影响,应用等高线图的方法,通过15组星点设计数值模拟方案的结果,绘制径向载荷峰值均值F1、轴正向载荷峰值均值F2、轴负向载荷峰值均值F3、总载荷峰值均值F4的等高线图,如图4~7所示。

图4 径向载荷峰值均值等高线
(1)由图4a~7a可知,当切削厚度h、振动频率f保持不变时,随进给速度v提高,径向载荷峰值均值F1、总载荷峰值均值F4明显增大;轴正向载荷峰值均值F2、轴负向载荷峰值均值F3略微增大;随进给速度v提高和切削厚度h增加,两者影响相同,使得径向载荷峰值均值F1、总载荷峰值均值F4呈明显增大趋势,交互作用明显。轴正向载荷峰值均值F2、轴负向载荷峰值均值F3呈明显增大趋势,交互作用不明显。

图5 轴正向载荷峰值均值等高线
(2)由图4b~7b可知,当进给速度v、振动频率f保持不变时,随切削厚度h增加,径向载荷峰值均值F1、轴正向载荷峰值均值F2、总载荷峰值均值F4明显增大;轴负向载荷峰值均值F3略微减小;随切削厚度h增加和振动频率f增大,两者影响相反,使得径向载荷峰值均值F1、总载荷峰值均值F4呈先增大后减小趋势,交互作用显著;轴正向载荷峰值均值F2呈增大趋势、轴负向载荷峰值均值F3呈减小趋势,交互作用不显著。

图6 轴负向载荷峰值均值等高线
(3)由图4c~7c可知,当进给速度v、切削厚度h保持不变时,随振动频率f增大,径向载荷峰值均值F1、总载荷峰值均值F4明显减小;轴正向载荷峰值均值F2、轴负向载荷峰值均值F3略微减小;随振动频率f增大和进给速度v提高,两者影响相反,使径向载荷峰值均值F1、轴负向载荷峰值均值F3呈先增大后减小趋势,交互作用比较显著;轴正向载荷峰值均值F2数值、总载荷峰值均值F4呈增大趋势,交互作用不显著。
根据等高线图4所示,在径向载荷峰值均值F1不大于55 kN的情况下,提高进给速度v和增加切削厚度h取值以提高截割煤岩效率,降低振动频率f取值降低消耗,确定进给速度v、切削厚度h、振动频率f的取值范围分别为450~600 mm/s、10~25 mm、30~45 Hz。

图7 总载荷峰值均值等高线
2.3 熵值法综合评价
以碟盘刀具的径向载荷峰值均值、轴正向载荷峰值均值、轴负向载荷峰值均值、总载荷峰值均值、总载荷曲线均值和总载荷盒维数6个响应综合最小为目标。在多目标的实验中,由于各响应的量级不同、取值范围不同或优选条件间存在相互矛盾。熵值可作为判断一个事件的随机性及无序程度,也可判断某个指标的离散程度,指标的离散程度越大,该指标对综合评价的影响(权重)越大,其熵值越小。因此,将数值模拟设计的结果用熵值法进行综合评价,来考察响应的综合效果。
依据星点设计实验,6组响应中分别有15组指标,对欲达到最大化与最小化的响应进行归一化处理:
(5)
式中:Fmax——每组响应中最大值;
Fmin——每组响应中最小值。
基于径向载荷峰值均值、轴正向载荷峰值均值、轴负向载荷峰值均值、总载荷峰值均值、总载荷曲线均值、总载荷盒维数对目标影响程度,通过熵值法得到权重系数分别为0.170 4、0.182 7、0.161 7、0.180 1、0.131 2、0.173 9,计算出6个响应值间的综合评价分Wi为
Wi=0.170 4dF1+0.182 7dF2+0.161 7dF3+0.180 1dF4+0.131 2dF5+0.173 9dF6。
(6)
根据式(6)计算求15组数值模拟综合评价值,如表3所示。

表3 15组数值模拟综合评价值
由表3可知,综合评价值最小的为第12组数值模拟。由数值模拟综合评价值可知,当切削厚度和振动频率不变时、提高进给速度,综合评价值Wi明显减小;当进给速度和振动频率不变时,增加切削厚度,综合评价值Wi明显减小;当进给速度和切削厚度不变时,增大振动频率,综合评价值Wi明显增大。对综合评价值Wi减小的影响从大到小依次为:增大切削厚度、提高进给速度、减小振动频率。
3 回归模型的验证
3.1 数值模拟与回归模型对比
结合等高线图分析后的确定3因素取值范围,为避免振动频率过大增加比能耗、提高截割煤岩效率、减小碟盘刀具所受载荷,选取一组截割参数v=570 mm/s、h=22 mm、f=45 Hz进行数值模拟。对应的数值模拟结果、回归模型预测值、偏差如表4所示。
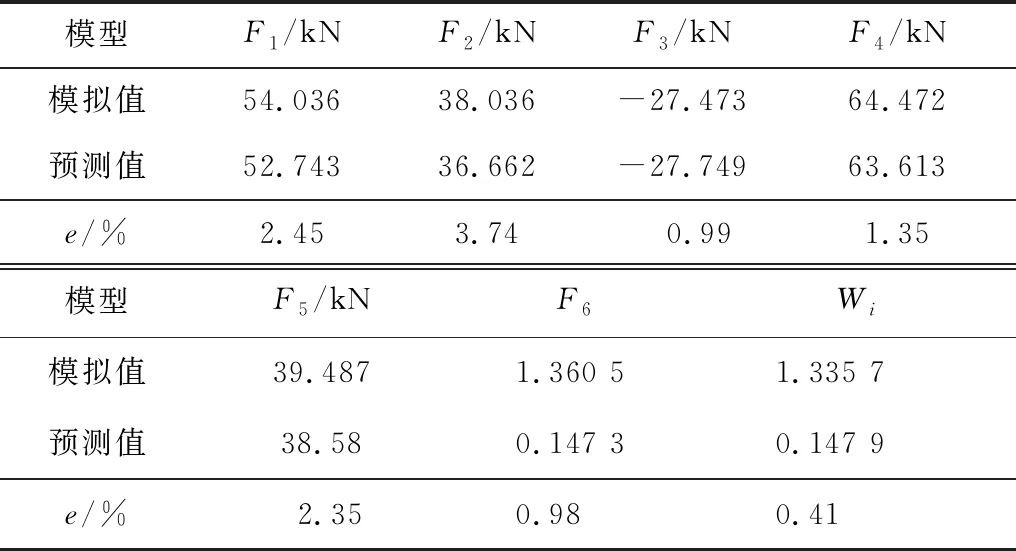
表4 数值模拟与预测值的对比
由表4可知,数值模拟与回归模型预测值相比,各响应值最大偏差为3.74%,平均偏差为1.98%,回归模型准确。与表2综合评价值最小的数值模拟12相比,综合评价值大5%,径向载荷峰值均值小7%,总载荷峰值均值小18%,振动频率减小11%。
3.2 实验结果与回归模型对比
为了验证回归模型的准确,将回归模型计算的径向载荷峰值均值与实验载荷谱径向载荷峰值均值进行对比。在实验参数v=300 mm/s,f=45 Hz不变时,改变切削厚度h分别为10、20、25 mm进行碟盘刀具振动切削截割煤岩实验后获得的径向截割载荷谱,如图8所示。

图8 不同切削厚度下径向载荷
将碟盘刀具振动切削截割煤岩实验获得的截割载荷谱的径向载荷峰值均值与回归模型(3)中F1进行预测的结果对比分析,如表5所示,最大偏差在17%以下。

表5 不同切削厚度下实验值与预测值的比较
在实验参数v=300 mm/s,h=10 mm不变时,改变振动频率f分别为40、45、50 Hz进行碟盘刀具振动切削截割煤岩实验后获得的径向截割载荷谱,如图9所示。

图9 不同振动频率下径向载荷
将碟盘刀具振动切削截割煤岩实验获得的截割载荷谱的径向载荷峰值均值与回归模型(3)F1中进行预测的结果对比分析,如表6所示,最大偏差在17%以下。6组实验平均偏差为14.19%。
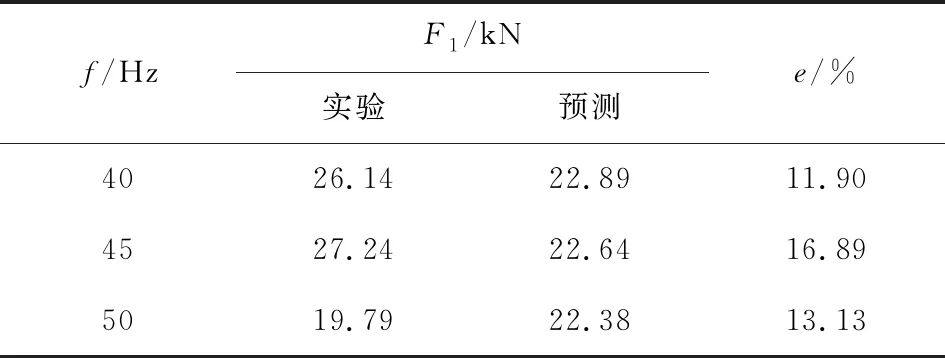
表6 不同振动频率下实验值与预测值的比较
4 结 论
(1)设计了进给速度、切削厚度、振动频率3因素5水平的星点设计数值模拟方案。通过绘制等高线图,分析了进给速度、切削厚度、振动频率对径向、轴正向、轴负向和总载荷峰值均值的影响。
(2)采用熵值法对6个响应分配权重,综合评价了碟盘刀具截割煤岩性能,增大切削厚度、提高进给速度、减小振动频率对综合评价值Wi减小的影响依次减小。
(3)根据数值模拟结果建立的回归模型,数值模拟结果与回归模型预测值最大偏差为3.74%,平均偏差为1.98%;实验载荷谱径向载荷峰值均值与回归模型预测值最大偏差为16.89%,平均偏差为14.19%。

