物联网感知数据边缘卸载机制研究*

袁培燕,耿丽娟,张 豪

(河南师范大学计算机与信息工程学院,河南 新乡 453007)

1 引言

目前，可穿戴设备、智能家居和智慧医疗等物联网应用发展迅速，产生了海量感知数据。如果将数据直接发送至云计算平台，产生的流量会给当前的骨干网络带来沉重负担。此外，传感器和数据中心之间的距离会造成长时间的传输延迟，导致用户体验不好。相比之下，边缘网络设备逐渐具备一定的计算、存储和通信能力，因此在边缘设备附近处理物联网设备的感知数据，可满足物联网应用海量数据分析的需求。在这种情况下，物联网感知终端将数据发送至边缘而不是云计算平台，以减少骨干网络流量。当感知数据到达时，边缘节点负责处理数据，然后响应用户或将处理后的结果发送至云端。

考虑到单个边缘服务器计算资源有限，如果单独处理收到的任务请求，过量的工作负载将导致一定的排队延迟，影响用户体验。在这种情况下，假定计算任务可分割，则可将一部分任务卸载到云层进行处理。显然，从边缘服务器的角度出发，确定最优的边缘卸载比例是一个值得关注的问题。本文以物联网设备能耗为约束条件，最小化任务的卸载时间，具体来说：

(1)假定边缘服务器设备可以使用本地计算资源处理其感知终端设备Di发送的工作负载的一部分为αi，1≤i≤n,n为物联网中感知终端设备的数量,αi=0意味着将所有接收的工作负载转发到云层。

(2)考虑边缘服务器设备的计算功耗和物联网应用设备的响应时间，将最优卸载比例问题表述为一个受能耗约束的响应时间最小化问题，然后使用序列二次规划算法进行求解。求解出最小响应时间下的最优卸载比例αi。在此基础上分析边缘服务器设备单位时间内处理的最大工作负载μ对响应时间的影响。

本文的其余部分组织如下:第2节回顾相关的工作，第3节建立模型，第4节进行建模与求解，第5节进行仿真并对结果进行分析，第6节对全文进行总结。

2 相关工作

在边缘计算中，对物联网感知数据卸载的研究刚刚起步。大多数研究[1 - 3]是在数据卸载的过程中寻找一个中继节点，中继节点参与数据的传输，但不对数据做任何处理。例如，文献[1]使用随机线性网络编码来传输数据，当车辆进入路边设备RSU(Road-Side Unit)的覆盖范围时，将编码数据发送给RSU，RSU再将数据转发给数据中心。文献[3]使用移动节点来帮助传感器收集感知数据，当移动节点进入传感器的覆盖范围时，传感器将数据发送给移动节点，移动节点再将数据传输至云端。此外，可以利用边缘设备有限的计算资源，将全部数据优先卸载到边缘设备中进行处理。如文献[4]提出一种计算卸载架构，利用资源受限的物联网设备附近的可用计算资源，优先将任务转移到附近有空闲资源的边缘网络设备上。文献[5]提出了一种基于宽带约束的局部物联网分流技术，充分利用网关资源提高带宽的使用效率，降低系统能耗。文献[6]提出一种数据上传框架PTDU(Pu- blic Transit Data Uploading)，利用PTS(Public Transit System)的优势，将PTS作为传送数据的中继节点。文献[7]为了提高数据传输的可靠性和处理速度，提出了一种基于简化变量邻域搜索的传感器数据处理框架。

需要指出的是，考虑到边缘设备的计算资源和存储资源有限，并不是所有的传感器数据都可以在边缘服务器进行本地处理。为了更好地提供服务，边缘服务器卸载数据的比例也成为研究的重点。文献[8]将排队系统分为表征局部队列和远程队列2类，考虑2类队列状态信息对计算卸载的影响，构造了一个多变量决策框架优化计算约束的MEC系统的延迟性能。文献[9]将联合负载均衡与卸载问题转换为一个混合整数非线性规划问题，以使系统效用最大化，通过联合优化选择决策、卸载和计算资源，提出了一种低复杂度的联合优化算法。文献[10]通过联合优化智能移动设备的计算速度、传输功率和卸载比例来研究部分计算卸载问题，并扩展到多个云服务器系统。文献[11]考虑到网络的利用率，提出了一种基于网络利用率和卸载偏好来确定卸载比例的卸载算法。文献[12]提出了基于吸引子的能够自适应选择最优卸载比例的算法。该算法基于吸引子活动自适应地调整卸载比例，能快速、自适应地对环境变化做出响应。

3 系统模型构架

本文考虑3层边缘计算架构场景，如图1所示，该场景包含n个物联网感知终端，基站与边缘服务器相连。由于物联网设备不具备数据处理能力，故其数据需上传至边缘服务器进行处理。受计算能力和存储能力的限制，边缘服务器只能处理部分数据，其余的数据需传输至远程数据中心进行远端处理。

Figure 1 Single cell edge calculation scenario

假设每一个物联网感知终端设备Di(1≤i≤n)传输到其通信范围内的边缘服务器的任务负载到达率为λi(如果在其通信半径内有多个边缘服务器，感知终端设备选择距离最近的一个进行传输，则由自由空间传播模型可知，其信噪比相对较大)，且λi为常量。由于任务负载可分割，用αi表示Di传输到某个边缘服务器的任务负载的比例。αi=1，表示边缘服务器处理所有的任务负载；αi=0，表示边缘服务器将所有的任务负载转发至云层数据中心进行处理。

4 问题建模与求解

4.1 问题的建模

本文的目标是考虑卸载比例与访问延迟之间的关系，并在能耗约束下使用户的访问延迟达到最小，使系统性能达到最优。考虑到2个性能指标：物联网应用的响应延迟和边缘服务器的能量消耗。边缘服务器单位时间的能耗表示如式(1)所示：

(1)

该指标表示边缘服务器卸载每单位任务负载所花费的能量，即边缘服务器卸载每单位任务负载的电能消耗。边缘服务器消耗的总功耗取决于静态功耗Ws和动态功耗Wd，静态功耗又称泄露功耗，主要是由泄露电流引起的，与边缘服务器计算资源的使用无关，动态功耗由计算资源的使用决定[13]。

边缘服务器的能耗效率η表示为：

(2)

响应时延主要包括感知终端设备与边缘服务器之间传输任务负载的往返时延和任务负载在边缘服务器上处理时的逗留时间。设τi为任务负载在边缘服务器与感知终端设备之间的平均往返时延。另外，本文假设边缘服务器处理任务卸载请求属于M/M/1排队系统。由排队论可知，其顾客源是无限的，且服从泊松分布。假设所有设备的任务负载到达率平均值为λ，边缘服务器单位时间的最大处理能力为μ。任务在系统中的逗留时间(包括等待时间和处理时间)则服从参数为(μ-λ)的负指数分布，在系统中任务负载的平均逗留时间为1/(μ-λi)。本文处理任务负载包括以下3种情况：

(1)αi=0。

此时边缘服务器通过骨干网络直接将接收到的所有任务负载全部转发到云数据中心。由于云数据中心通常配置高性能任务负载处理单元，处理任务负载的响应时间要比任务负载传输的时间短得多，因此假设云数据中心处理每个边缘服务器转发的任务负载所造成的延迟可以忽略不计。在此种情况下，物联网感知终端应用的平均响应延迟表示可如式(3)所示:

Ti(αi)=τi+τc

(3)

其中，τc为边缘服务器与云层之间传输单位任务负载的往返时间。边缘服务器没有使用任何计算资源来处理其接收到的任务负载，所以能量消耗将不依赖于物联网应用的响应延迟，故式(3)为边缘服务器向应用提供的响应延迟的阈值。

(2)αi=1。

边缘服务器使用本地资源独立处理接收的所有任务负载。在这种情况下，云数据中心不参与任务负载的处理，故物联网应用响应延迟只包括物联网感知终端与边缘服务器之间的传输延迟和在边缘服务器上处理所用的时间。此时Di与边缘服务器之间的平均响应时延Ti可表示如式(4)所示：

(4)

(3) 0<αi<1。

此时应用的平均响应延迟为：

(5)

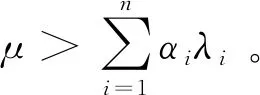
本文的主要目标是在给定的能耗功率约束下，设计分配任务负载策略，使物联网应用的平均响应时延Ti最小化，即：

(6)

4.2 问题求解

本文的优化问题可具体表示如式(7)所示：

(7)

式(7)中的目标函数的一阶导数为：

(8)

(9)

由于Pi>0，目标函数的一阶导数存在且二阶导数大于零，满足凸函数的判定条件[14],故优化问题在定义域内存在最优解。

(10)

(11)

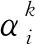
令C和H分别表示目标函数的一阶导数和二阶导数，令B和A分别表示函数g和g的一阶导数组成的向量。有:

(12)

即二次规划问题的一般形式为：

s.t.AS≤B

(13)

有效集算法可以求解此二次规划问题的一般形式。由定理1知[15]，可构造一个集合序列逼近有效集，从初始可行点S0出发计算有效集Q(S0)，解对应的等式约束子问题。重复上述过程，得到有效集序列{Q(Sk)},k=0,1,…，求得一般形式二次规划问题的最优解。

定理1设S*是一般凸二次规划问题的全局极小点，且在S*处的有效集为Q(S*)=E∪I(S*)，则S*也是下列等式约束凸二次规划的全局极小点。

s.t.ahS-bh=0,h∈Q(S*)

(14)

其中,集合E和集合I(S*)分别是指等式约束集和不等式约束集，ah和bh均为等式约束中的系数。

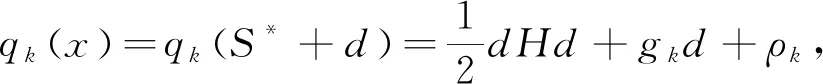
s.t.ahd=0,h∈Q(Sk)

(15)

其拉格朗日函数形式为：

(16)

其中，β为拉格朗日乘子。

令式(16)的一阶导数为零，可求得函数L(d,β)的解。

基于上述分析，有效集算法的步骤如算法1所示。

算法1求解二次规划子问题的有效集

1：Initializek=0,S0∈R;

2：Solve the subproblem described by equation (14), SetQk=E∪I(Sk);

3：Solve equation(16)to get the minimumdkequation and the Lagrange multiplierβk;

4：ifdk≠0then

5：gotoline 15;

6：else

7：gotoline 9;

8：endif

10：if(βk)t≥0 then

11：Skis the global minimum point;

12：else

13： Select one constraint that makes theβksmaller than zero,gotoline 2;

14：endif

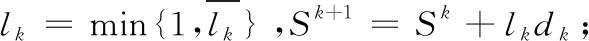
16：iflk=1 then

17：Qk+1=Qk;

18：else//lk<1

19：Qk+1=Qk∪{jk};

20：endif

21：k=k+1;gotoline 2;

综上，序列二次规划(SQP)算法的迭代步骤如算法2所示。

算法2序列二次规划

3:The optimal solutionS*is obtained from Algorithm 1, then letSk=S*;

7：else

8：gotoline 10;

9：endif

10：Fix Hessian matrixHk+1;Letk=k+1;gotostep 2;

5 仿真结果

图2表示当边缘服务器μ=100时，平均响应延迟Ti与卸载比例αi之间的关系。由图2可知,平均响应延迟随卸载比例的增大而减小，当任务负载到达率大大超过边缘服务器的处理速率时，由于长队列延迟，平均响应时间呈指数增长。另一现象是随着任务负载λ的逐渐增大，边缘服务器的最优卸载比例α将逐渐减小，同时平均响应延迟也将逐渐增大。

Figure 2 Relationship between α and T

图3显示当任务负载到达率λ=100时，在边缘服务器处理速率μ不同的条件下，平均响应延迟T与卸载比例α之间的关系。从图3中可以看到，最优卸载比例与边缘服务器处理速率μ呈正相关，平均响应延迟与μ则相反。特别地，当边缘服务器的处理速率远大于任务负载到达率时，最优卸载比例将为1，此时边缘服务器将处理所有的任务负载，物联网应用的平均响应延迟将达到最小值。

Figure 3 Relationship between α and T when λ=100

图4显示在边缘服务器处理速率μ=150时，任务负载到达率和最优卸载比例之间的相关性。从图4中可以看到，当任务负载到达率λ小于边缘服务器处理速率μ时，边缘服务器将处理所有任务负载；当任务负载到达率λ大于边缘服务器处理速率μ时，二者负相关，即任务负载到达率越高，卸载比例越低。此外，图5显示了平均响应延迟T随任务负载到达率λ的变化情况。在边缘服务器处理速率不变的情况下，队列延迟随着数据量的增大而增加，应用的平均响应延迟也随之增大。

Figure 4 Relationship between λ and α

Figure 5 Relationship between λ and T

以上都是在能量阈值一定的条件下，分析各参数对所提解决方案性能的影响。图6和图7是平均响应时延和卸载比例随能量阈值的变化趋势。实验中设定边缘服务器的处理速率μ=100，任务负载的到达率λ=150。从图6中可以看到，随着能量阈值的增加，卸载比例增大到一定值后便保持不变。出现这种现象的原因是任务负载在边缘服务器上的卸载处理属于M/M/1排队模型，为使模型趋于稳定，边缘服务器的处理速率必须大于任务负载到达率，即μ>λ，剩下的任务负载将由边缘服务器上传至云层数据中心处理。因此，当能量阈值增大到一定程度后，约束条件μ>λ起主要作用，此时卸载比例便不会随能耗阈值的增大而增大。同样地，在图7中，由于卸载比例不能随着能量阈值的增大而无限增大，应用的平均响应延迟也会减小到一定值后保持不变。

Figure 6 Relationship between η and α

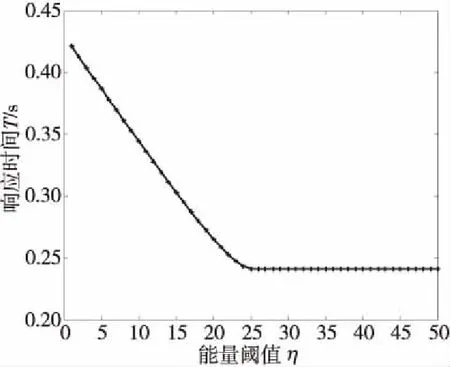
Figure 7 Relationship between η and T

为了进一步验证所提解决方案的性能，本文引入了以下2种基准测试方案。一种是没有卸载(NO)方案，NO方案表示边缘服务器不在本地卸载感知数据的情况，即α的值等于零。另一种是完全卸载(FO)方案，在FO方案中，所有的传感器数据都是在边缘服务器本地进行处理，即α=1。图8显示了3种方案中每种方案的平均响应延迟随任务负载到达率的变化趋势，其中PO表示本文提出的部分卸载方案。由于NO方案是将所有的任务负载上传至云层处理，故其平均响应时延只包括单位任务负载的往返传输时间，由于网络带宽一定，不同的任务负载到达率的传输速率不同，因此单位时间的传输延迟与任务负载到达率成正比。因此，可以把NO方案中的响应延迟作为物联网应用响应延迟的上限。值得注意的是FO方案，当任务负载到达率λ大于边缘服务器的处理速率μ=150时，根据M/M/1排队模型应用的平均响应延迟趋于无限。从图8中可以明显看出，当λ≥μ时，PO方案具有最佳的延迟性能。

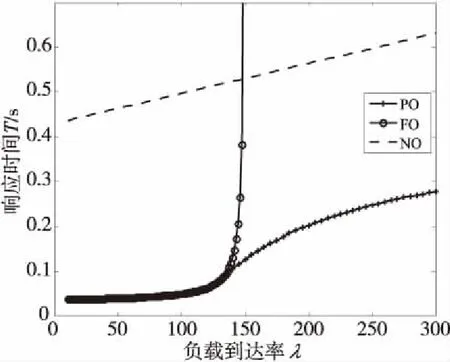
Figure 8 Response time of three unloading schemes

6 结束语

本文研究了移动边缘场景下物联网应用终端设备感知数据量的最优卸载比例问题。考虑了2个性能指标：边缘服务器的平均响应延迟和能量消耗。通过将这2个指标表示为一个最小化问题，利用序列二次规划算法给出了该问题的最优解。本文分析了不同任务负载到达率对最优卸载比例和访问延迟的影响，并将提出的解决方案与基准方案进行了对比。仿真结果表明，本文所提方案在任务负载到达率大于边缘服务器处理速率的情况下具有最佳的延迟性能。