基于隐马尔可夫模型的多真值发现算法*

王会举，李孟萱，黄卫卫，周秋怡

(中南财经政法大学信息与安全工程学院,湖北 武汉 430073)

1 引言

信息时代，多个数据源对同一对象的描述可能并不相同甚至相互之间存在矛盾和冲突，数据之间的不一致性无可避免。根据“垃圾进，垃圾出(Garbage in,Garbage out)”原则，错误数据极有可能导致错误的结论与决策。“数据丰富，信息贫乏”的困境反映出当前数据与信息量严重不对等、数据质量低劣、利用率不高等问题[1]。因此，从可能存在矛盾的观测值中找到目标对象的真值，可以有效提高数据质量，保证数据使用人员分析和决策的准确性。然而，现实事物通常拥有多值属性，如一部电影由多人主演甚至导演、一本图书可能由多位专家共同创作。这类对象存在多值属性的问题被称为多真值发现问题。

本文基于图模型构造了一个新的多真值发现算法，可有效提高真值发现算法的正确率。主要贡献有以下3点：

(1)在传统投票方法的基础上，设计出改进的初始真值的确定CVote(Cluster Vote)算法，该算法能够更好地应用于多真值发现研究。

(2)设计了真值发现中一种类似于隐马尔可夫模型的转移矩阵的“可靠性转移矩阵”，并据此提出了基于图模型的真值发现算法GraphTD(Graph Truth Discovery)。

(3)提出了针对多真值发现研究的效果评价指标体系，能够从多个方面对真值发现的结果进行评价，并通过大量实验验证了GraphTD算法和CVote算法的有效性。

2 相关研究

为解决多源数据的冲突问题，研究者们进行了众多研究，目前的真值发现方法可概括为3类，分别是迭代方式、概率模型方式和图模型方式。

(1)迭代方式，即同时计算描述和数据源可靠的程度。Yin等[2]最早于2008年提出了真值发现的定义，并提出经典的TRUTHFINDER算法迭代计算对象的真值和数据源的可靠性。在此基础上，国内外相关学者从不同角度对算法进行了改进。王继奎等[3]提出了一种非对称的数据值相似度计算方法，并基于明确度和敏感度，从被动错误和主动错误两方面入手，提出了一种冲突数据源质量评价算法[4]。考明军等[5]将数据源的权威性纳入考虑范围，对数据源在投票时的比重进行了调整，是对传统的投票法的创新性改进。文献[6,7]则基于EM(Expectation Maximization)算法构建出真值计算的最大似然函数，并迭代计算出对象的真实观测值，为真值发现问题提供了一种新的研究思路。文献[8-10]针对同一数据在不同数据源之间的复制特性，在数据源不独立的基础上，设计了基于数据间复制检测的真值发现算法。

(2)概率模型方式。文献[11,12]基于概率图模型将真值发现用于药物副作用发掘中；董微等[13]构造了基于贝叶斯公式的概率模型，并将真值发现应用到学术资源集成中；Wan等[14]提出了KDEm(Kernel Density Estimation from Multiple Sources)算法，该算法是一种全新的基于概率的研究方法，从变量的角度出发利用核密度估计计算得到对象的真值。Xin等[15]通过在新的多层概率模型中使用联合推理来区分提取过程中的错误与Web源本身中的错误，以此来计算数据源的真实可信度水平。

(3)图模型的方式。王继奎等[16]将HITS(Hypertext-Induced Topic Search)中视图的思想引入真值发现研究中，基于图模型实现了对象观测值集的建模，继而设计了迭代式多真值计算算法。Yin等[17]提出了一种半监督的真值计算算法，该算法基于图模型对描述之间的关系进行定义，并提出了基于图模型的损失函数，明显提高了真值发现的准确率。文献[18,19]针对数据源的可靠性计算，考虑数据源的主动错误与被动错误，分别研究了基于图和基于贝叶斯的迭代计算方法，有效提高了真值发现的准确率。Fang等[18，20,21]从数据源的角度出发，利用图模型模拟了数据源之间的关系，并将数据的长尾现象等多种因素纳入考虑范围，是真值发现领域中一种全新的解决方案。

现有研究虽从各方面对真值发现进行了探索，但依然存在初始真值的选择过于简单、算法的复杂度较高、未考虑结果集排序、评价指标较为单一等问题。本文构造了一种图模型上运算的真值发现算法，通过将真值发现问题转换为图模型并利用转移矩阵进行求解，大大简化了真值发现的计算过程。

3 GraphTD多真值发现算法

3.1 真值发现的定义

从存在矛盾或冲突的多个数据源中找到同一个对象最准确的观测值即为真值发现问题。

为给出真值发现的数学定义，首先定义相关的概念和数学符号。本文可靠性、可信度、置信度表示同一含义，后文将不做具体区分。

o：表示待研究对象的属性，比如作者是图书的属性之一。在本文的研究中，考虑的是对象的单一属性，即在研究图书时仅研究其作者属性，不讨论图书出版社、页数和国籍等属性，因此，本文在后面的表述中，对象与对象的属性将不再区分，表示的是相同的概念。O={o1,o2,…,oN}表示所有对象的集合。

s：表示数据源，数据源提供了各研究对象的观测值。S={s1,s2,…,sK}是数据源的集合。

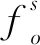
t：代表经算法计算得到的真值，也就是在对同一个对象的多个描述中，经计算后被认为是真值的f*(但该值不一定是对象的真值，只是在多个观测之中选择的最优解)。to表示对象o的真值。

p(f)：表示描述置信度的高低，也就是对象的观测值是真值的概率，p(f)越大，该描述为真值的概率越高。p(f)的取值在[0,1]。

p(s)：代表了数据源可信度的高低，p(s)越大，表示数据源越值得信任，那么该数据源就越有可能提供对象的真值。p(s)的取值在[0,1]。

sim(fi,fj)：代表了2个观测值fi和fj相互支持度，即当fi(fj)的观测值为真时，fj(fi)观测值也为真的概率。本文用相似度来计算支持度。

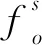
为从多个矛盾描述中找到对象的真值，本文做出如下假设：

假设1数据源越可靠，其提供的描述越可信，并更有可能成为真值。

假设2数据源提供的真值越多，该数据源越可靠。

假设3每个对象的真值为一个非空集合。

3.2 真值初始化算法CVote

投票(Vote)法是现有研究中最常使用的初始值选择方法，直接选择出现次数最多的描述作为对象的真值。然而，Vote法认为所有的数据源的可靠性是一致的，在数据集成的多源数据冲突问题中，简单的Vote法很可能将错误的数据当作真值。此外，Vote法只能处理单真值问题，而无法处理多真值问题，具有很大局限性。因此本文提出一种改进的多真值发现CVote算法。

CVote算法采取细粒度投票机制，其核心思想为：将一个对象的K个描述的集合当做一个聚类；一个描述同其他描述的类内汉明距离和越小，越说明其他描述与该描述较相似，则该描述越有可能代表整体描述所表达的核心思想，因而越可能成为对象的初始真值。其计算方法为：对于每一个描述fi，选其为聚类中心点(初始真值)，计算其他描述与它的汉明距离之和SEi(i=1,2,…,K)。CVote算法如算法1所示。

算法1CVote

输入：包含对象及多个数据源对对象的描述的数据集。

输出：每个对象的真值。

步骤1取出数据库中的N个对象及K个数据源对对象的描述。

步骤2对于N个对象：

将K个数据源的描述向量化；

步骤3对于K个数据源：

计算该数据源的描述与其他数据源的描述的汉明距离之和sumHamming[k]。

步骤4汉明距离之和最小时对应的数据源的描述就是对象的真值。

这里定义的多真值发现算法有2个基本点：(1)在计算真值时，该算法单独考虑了描述中出现的每个值，而不是简单地将描述作为一个整体。(2)将汉明距离之和最小时作为聚类中心点的观测值当作对象的真值，汉明距离之和是选取对象真值的重要依据。

3.3 GraphTD真值发现图模型构建

在GraphTD真值发现算法中，将对象的观测值作为图模型中的节点，并根据数据源和观测值之间的关系，计算得到状态转移矩阵，用初始状态和状态转移矩阵迭代计算得到描述为真的概率的收敛值。一个对象的真值是具有最高概率值的描述。

本文借鉴Yin 等[17]的做法，将描述作为节点，并通过在同一个对象的描述节点间和来自同一个数据源的节点间建立联系边，形成隐马尔可夫模型中的一个时刻状态。如图1所示，f1和f3描述同一个对象o1，f2和f4描述同一个对象o2，f1、f2和f3、f4分别来自数据源s1和s2，依据前面所定义的规则，将描述了同一个对象的f1与f3、f2与f4分别连接起来，来自于同一个数据源的f1与f2、f3与f4分别连接起来。

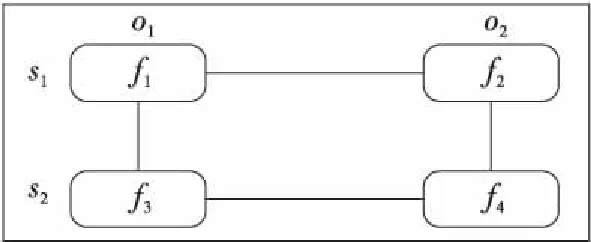
Figure 1 Graphic model of object description

为方便真值发现算法的讨论，下面给出GraphTD图模型的正式定义。

定义2(GraphTD图模型定义) GraphTD图模型可表示为三元组G=(V,E,w)，其中V为观测值集合，代表G的节点集；E=V×V代表观测值节点间的依赖关系，构成了G的边集；w为边上的权重，构成了可靠性转移矩阵。

定义3(可靠性转移矩阵) 即隐马尔可夫模型中的状态转移矩阵。可靠性转移矩阵是计算对象真值的主要依据，可基于观测值以及数据源之间的关系计算得出。

可靠性转移矩阵的计算是构建图模型后的关键步骤，本文依据边之间的依赖关系即GraphTD图模型中边的权重，来确定可靠性转移矩阵的元素值，根据观测值之间的边的类型(如描述同一个对象的边类型，或来自同一个数据源的边类型)计算得到。

权重的计算方法如下所示：

(1)对于来自于同一个数据源的观测值(节点)fi→fj，它们之间的边的权重为数据源的可信度乘以源节点的初始可信度，即p(si)·p(fi)；

(2)描述同一个对象的节点fi→fj，它们之间的边的权重用源节点的可信度乘以节点间的支持度表示，即p(fi)·sim(fi,fj)，衡量节点间相似性的指标是汉明距离；

(3)若节点之间无连接，则转移权重为0；

(4)在可靠性转移矩阵中，用观测值的初始可信度p(fi)表示。观测值本身的转移概率——也就是转移矩阵的对角线上的值fi→fi。

根据前面所提到的边的权重计算方法可以得到转移矩阵A，将转移矩阵按行归一化后即可得到可靠性转移矩阵A*。最后根据观测值的初始置信度与可靠性转移矩阵迭代计算，即可得到观测值为真的概率收敛值。

3.4 GraphTD真值发现算法

本文采用布尔表示的方法将对象的描述向量化，采用汉明距离来计算描述的初始置信度与描述之间的相互支持度。同时分别对描述的可信度、数据源的可靠性和描述间的相似性进行定义。

(1)数据源的可靠性。

本文用数据源提供的所有观测值的准确度的平均值表示数据源的可靠性。若用p(s)表示数据源的可靠性，F={f1,f2,…,fK}表示数据源的所有观测值的集合，p(f)表示描述f为真值的概率，则数据源s的可靠性p(s)可由式(1)得出：

(1)

(2)描述的可信度。

初始状态描述的可信度用描述与真值的相似度衡量。利用CVote算法得到对象的初始真值，并根据各观测值与初始真值的相似度计算出各观测值的可信度。描述同一个对象的数据用向量X表示，令真值的置信度为1，p(f)表示观测值f的可靠性,则描述f的可靠性可用式(2)表示：

(2)

(3)描述间相似性。

同一个对象的不同观测值的可靠性具有一定的关联，本文采用汉明距离衡量描述之间的相似性，并据此表示描述之间的支持度。设fi和fj表示对同一个对象的描述，则fi与fj之间的相似性可用式(3)所示：

(3)

其中，m是fi与fj之间的汉明距离。

基于以上公式，得到初始状态下观测值的可靠性、数据源的置信度和观测值之间的相似性后，可以根据GraphTD图节点及边关系计算出状态转移矩阵，然后迭代计算得到每个观测值可信度的收敛值，最后依据收敛值大小选出对象真值。

3.5 GraphTD算法总体描述

GraphTD真值发现算法总体框架如图2所示，算法核心思想是：基于可靠性转移矩阵迭代计算得到每个观测值置信度的收敛值，将对应收敛值最大的观测值当做对象的描述真值。由于不同初始真值会导致产生不同的可靠性转移矩阵，该算法的结果容易受到初始真值的影响。GraphTD算法的描述如算法2所述。

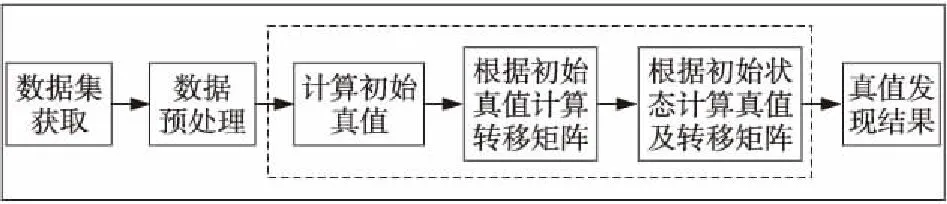
Figure 2 Overall framework of GraphTD

算法2GraphTD

输入：包含对象及多个数据源对对象描述的数据集。

输出：每个对象的真值。

步骤1确定对象的初始真值，并令初始真值的可信度为1。

步骤2计算对象的其他描述与初始真值的汉明距离，并计算其他描述的初始可信度。

步骤3根据描述的初始可信度计算数据源的可靠性。

步骤4根据数据源的可靠性、描述的可信度和描述之间的依赖关系来计算可靠性转移矩阵。

步骤5用初始状态描述的可信度乘以可靠性转移矩阵，如果算法收敛，则结束，否则重复步骤4。

步骤6根据描述可信度的收敛值选择对象的真值。

3.6 算法评价指标

现有研究一般仅用正确率来评价算法的好坏，维度较为单一。本文定义以下4个指标来更全面地衡量算法的性能。

定义4(错误率Acc0)Acc0衡量算法在真值发现时的错误率。

(4)

其中，ntotal_error为算法识别真值与对象真值完全不同的对象数。

定义5(正确率Acc1)Acc1衡量算法在真值发现时的正确率。

(5)

其中，ntotal_correct为算法识别真值与对象真值完全相同的对象数。

定义6(部分正确率Acc2)Acc2衡量算法在真值发现时的部分正确率。

(6)

其中，npartial_correct为算法识别出的真值仅是对象真值一部分的对象数。

定义7(部分错误率Acc3)Acc3衡量算法存在部分正确部分错误情况下的部分错误率。该指标与Acc2识别出的真值不完整但正确的情况不同，它的真值是部分正确的，而错误部分的真值中则包含错误数据，是不可靠的。

(7)

其中，npartial_error为算法识别真值部分错误的对象数。

4 实验构建及分析

4.1 数据集获取

本文通过网络爬虫技术，采集了中国图书网、豆瓣读书、淘书网、孔夫子旧书网和有路网等5个书籍电商网站的计算机相关书籍信息，对数据进行冗余剔除、规范化和数据合并等预处理操作后得到来自5个数据源的共89 897条不同书籍数据。

4.2 实验结果及分析

为了验证本文提出的CVote和GraphTD的有效性，本文在同一书籍作者数据集上分别实现了以下7种相关真值发现算法来与本文算法进行对比：

(1)Vote：基本的Native Vote投票算法。

(2)CVote：本文提出的真值初始化算法CVote。

(3)TFNoSup：不考虑描述之间相关关系的TRUTHFINDER算法。

(4)TF：Yin等[17]提出的经典TRUTHFINDER算法。

(5)AccuVote[22]：当前准确率最高的图真值发现算法。

(6)GTDVote(GraphTD with Vote Initialization Algorithm)：以Vote作为初始化算法的类GraphTD算法。

(7)GraphTD：以CVote作为初始化算法的GraphTD多真值发现算法。

实验中选取200条图书记录，并按照惯例，将图书封面上的作者选为真值，通过人工收集的方式得到真值的标准集。表1是3本不同图书的作者和各个算法在收集的数据集上计算得到的作者真值情况，根据这些数据，可以计算出各个算法的准确率——包括正确率、部分正确率、错误率、部分错误率。

根据3.6节定义的真值发现算法效果衡量指标，以人工收集的真值作为基准，对比分析算法识别的正确率。表2统计了各个算法的正确率、错误率、部分正确率和部分错误率。表2和图3显示了不同真值发现算法的对比结果。其中，Vote/CVote对比实验结果显示，CVote算法比Vote算法的正确率Acc1低，也就是在寻找与真值完全一致的观测值上CVote算法比Vote算法表现稍差。但是,在部分正确率Acc2上，CVote算法优于Vote算法，通过对原始数据的观察和比较可以发现，在得票相同的情况下，Vote算法会默认选择第1个观测值作为真值，该值由程序设置决定，较为随机，因此当数据源不多时，Vote算法的结果具有偶然性。而CVote算法考虑了描述之间的相关关系，因而更倾向于选择确定的真值，其抗干扰性更强。

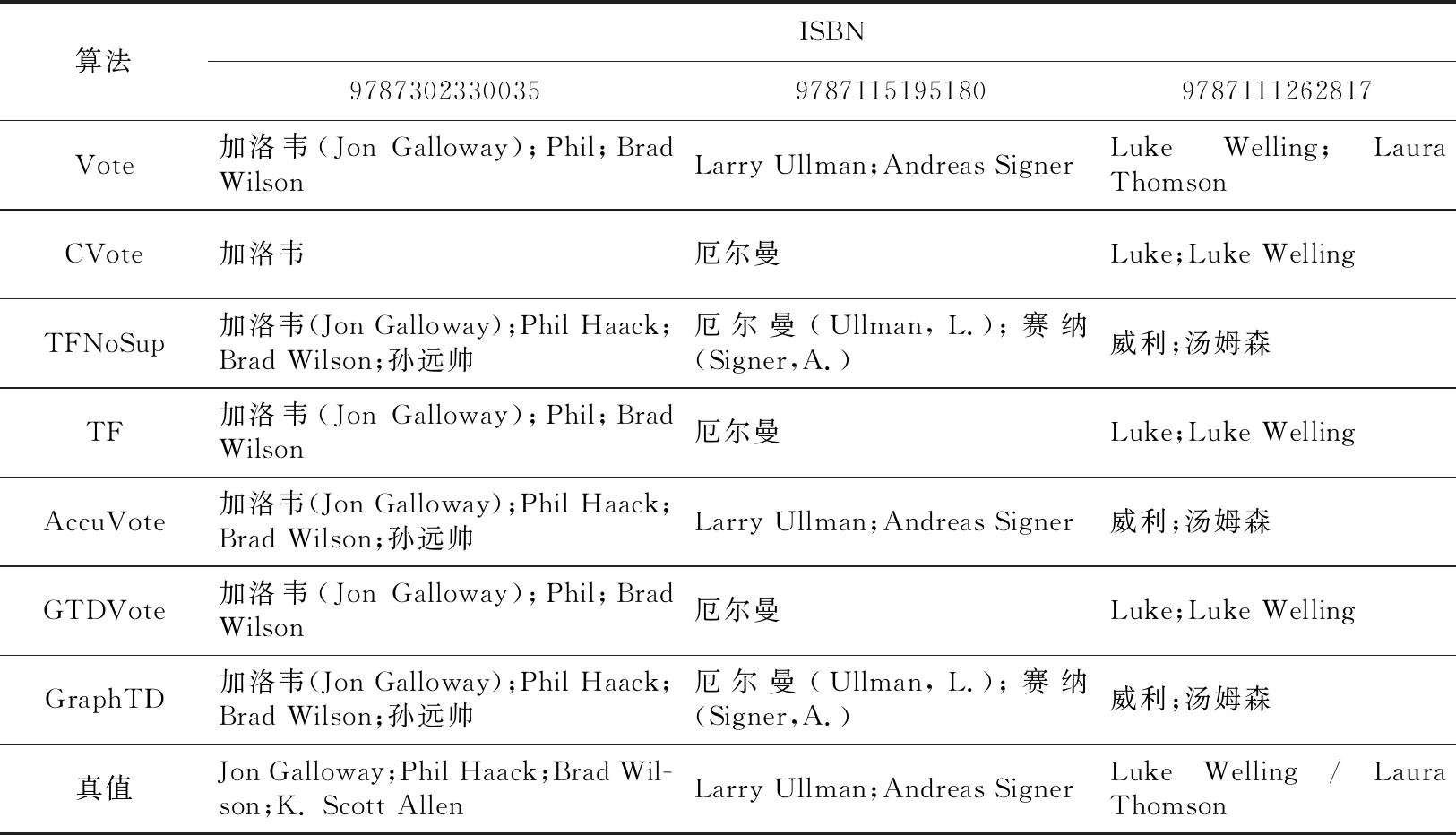
Table 1 Objects truth values and truth values recognized by algorithms

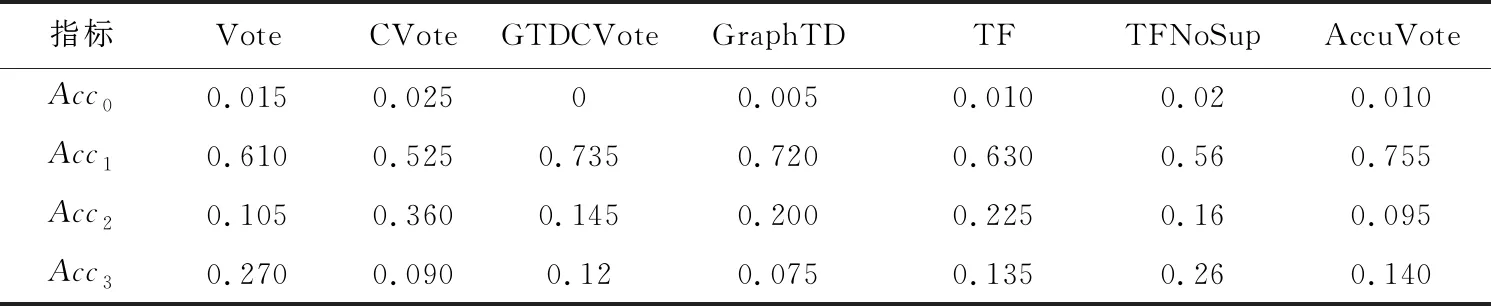
Table 2 Statistics of recognition results of each algorithm

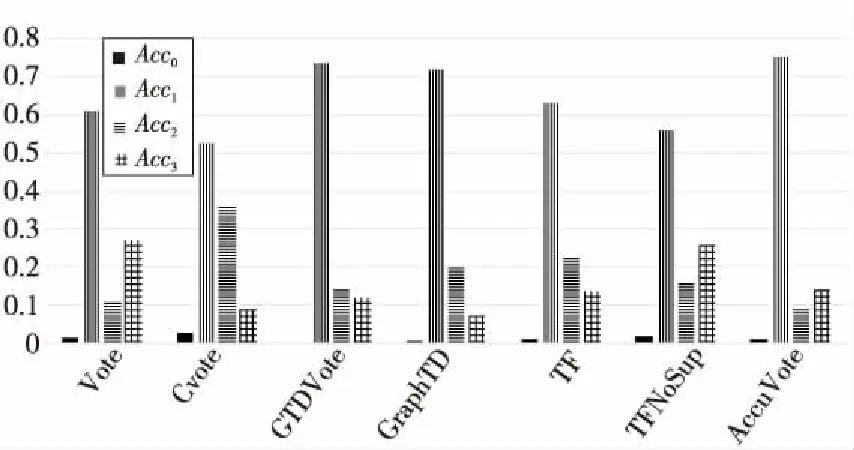
Figure 3 Results comparison of truth discovery algorithms

图4将Acc2与Acc1的和当做算法的整体正确率。从图4不难看出，CVote算法的表现要优于Vote算法，验证了CVote算法的可行性。

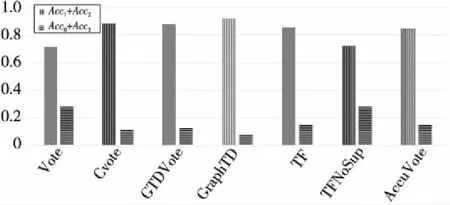
Figure 4 Comparison of the overall correct rate and overall error rate of truth discovery algorithms

类似地，从TFNoSup/TF对比实验中可知，TF算法的整体正确率和部分正确率均高于TFNoSup的，进一步证实了描述之间的相关关系对真值发现算法的准确率具有重要影响，这一点也体现在GTDVote/GraphTD的对比中。由图3和图4可以明显看出，虽然GraphTD在整体正确率上基本等于GTDVote的，但其部分正确率远高于GTDVote的，此结果与Vote与CVote的比较结果相同，说明对象最终真值的计算会受到初始真值的影响。考虑了描述间关系的算法往往具有更高的稳健性和抗干扰性，更能够避免数据源带来的偶然性问题。

此外，图3中显示，相比于传统的Vote/CVote和TFNoSup/TF算法，GTDVote/GraphTD算法的整体正确率有明显提升，仅比当前最准确的图真值发现算法AccuVote的略低，但GTDVote/GraphTD的部分错误率Acc3相比于AccuVote的有一定下降，特别是GraphTD的部分错误率明显低于AccuVote的。如果以Acc1与Acc2的和作为算法的整体正确率，Acc0与Acc3的和作为算法的整体错误率(如图4所示)，则GraphTD的整体正确率高于AccuVote算法的，说明GraphTD算法具有一定的性能优势。

5 结束语

本文基于隐马尔可夫模型，设计了一个GraphTD多真值发现算法，并在真实数据集上对算法进行了验证分析。实验结果表明，GraphTD多真值发现算法可有效提高真值识别的准确率，具有较强的可推广性。