基于Strcmp分解超Lorenz混沌的图像加密算法*

靳旭文，李国东

(新疆财经大学统计与数据科学学院,新疆 乌鲁木齐 830012)

1 引言

5G网络时代的到来正在加快无线大数据的增长，造成数据量急剧膨胀，信息由传统的文字信息慢慢转变为图像和视频。且互联网上时事资讯和聊天会产生海量的图像数据，因此，设计隐私保护的图像安全性问题近年来成为热点。

目前，数字图像加密算法主要是通过对图像像素点作位置和值的改变，从而经过置乱和扩散对图像完成加密。混沌系统是具有非常复杂的伪随机性的非线性系统，对控制参数和初始条件具有高度敏感性，任何微小的初始偏差都会被指数式放大，符合图像像素点扩散规则。同时，它可由非线性系统的方程、参数和初始条件完全确定[1]。1998 年，Fridrich[2]首次在图像加密中引入混沌模型，由此拉开了图像加密的新大门。由于混沌具有初值敏感性、无周期性和遍历性，微小变动初始值参数就可产生符合加密的源序列。李春虎等[3]提出利用Tent映射和Anorld相结合的算法进行加密，能够有效地扩展密钥空间。不过又被证明，随着时间周期的变换，混沌系统具有单一性及混沌性能退化等问题。接着研究者发现了具有更强混沌特性的超混沌系统，并引入其他学科工具结合混沌系统设计加密算法。例如，涂正武等[4]结合生物基因DNA规则，将腺嘌呤(A) 、鸟嘌呤(G) 、胞嘧啶(C) 和胸腺嘧啶(T) 4种碱基结合图像和混沌序列作变换从而完成加密，但是其规则库较小，可供DNA编码的方式单一。姚丽莎等[5]利用DNA编码与混沌系统相结合的加密方式，对原文分层加密，虽引入汉明距离作为初始值参数，但混沌系统特性仍会衰减。

为了解决以上加密算法中遇到的混沌特性衰减和序列编码规则库较小的问题，本文在数理命题逻辑逆运算的基础上设计Strcmp分解混沌序列的图像加密算法，对图像分块加密，创建密文熵反馈机制，使得混沌系统每次迭代时使用的控制参数都由加密完成的前一密文块所提供，从而产生双重加密源序列，进一步提升混沌特性和算法安全等级。

2 超Lorenz混沌系统

2.1 超Lorenz混沌

美国气象学家Lorenz是混沌理论的奠基者之一。20世纪50年代末到60年代初，他利用计算机模拟观测的天气预测值时发现，对模型初始条件的微小改变也会显著影响运算结果[6]。随后得到了有3个变量的一阶微分方程组，即Lorenz混沌：

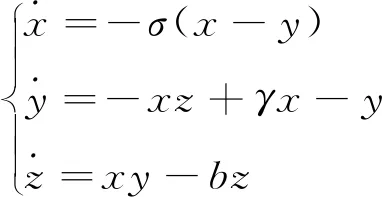
(1)

在式(1)第1个方程中引入变化律令并加入2个新的控制参数时变为超Lorenz混沌[7]，其中超Lorenz混沌系统的定义方程如式(2)所示：

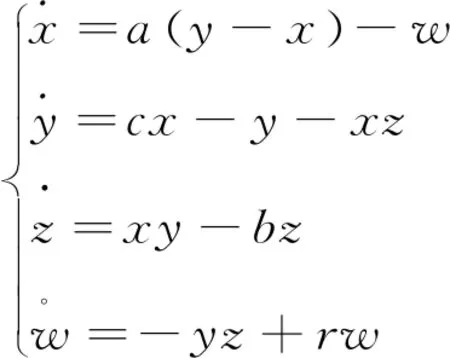
(2)

其中，参数值a=10,b=8/3,c=28,r=-1时，式(2)处于超混沌状态。利用其产生的混沌序列，可做出xn-yn相图、xn-zn相图、xn-wn相图、yn-zn相图、yn-wn相图和zn-wn相图,如图1所示。

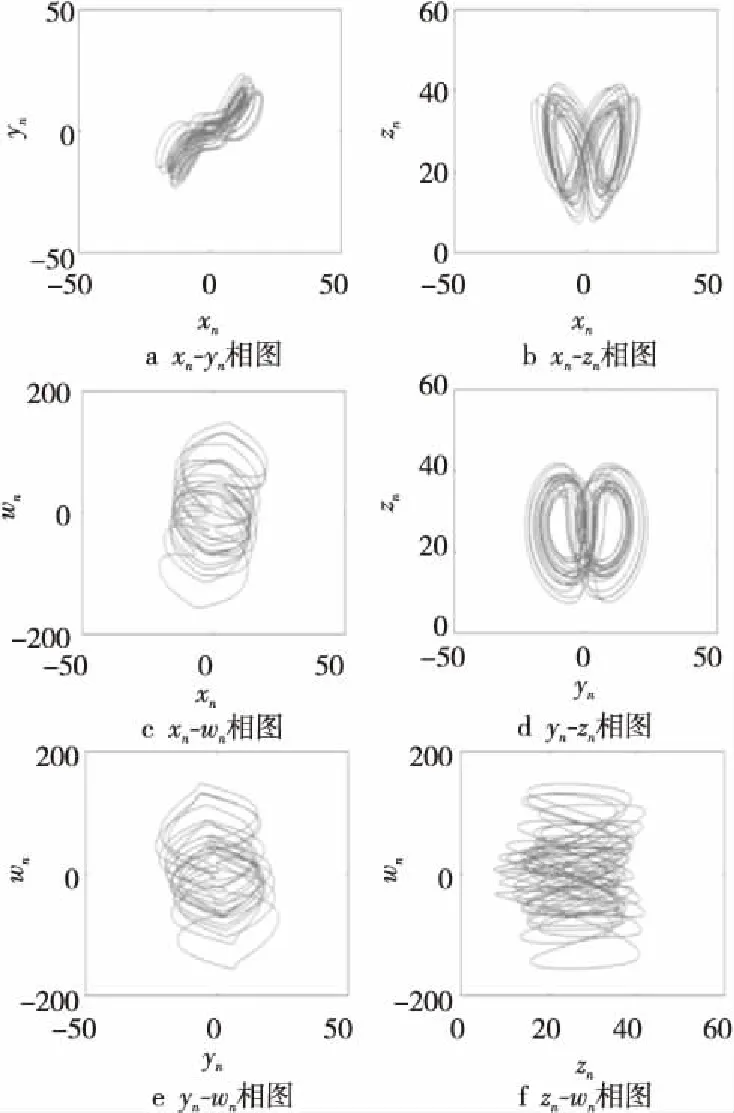
Figure 1 Phase diagram of hyperlorenz chaotic system

2.2 初值敏感性分析

对混沌系统的初始值x0、y0、z0、w0做微小改变，产生2组混沌序列，随机抽取200对做对比，作出相应位置散点分布图及其轨迹图，如图2和图3所示。

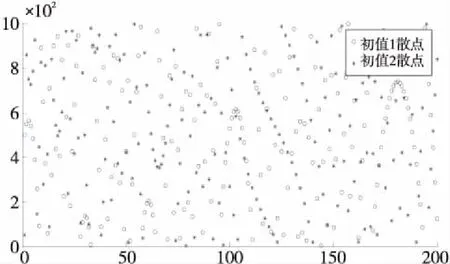
Figure 2 Scatter distribution of hyperlorenz chaotic system

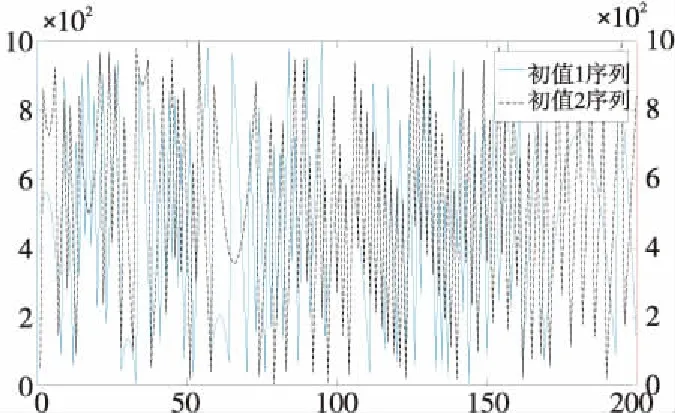
Figure 3 Strcmp sequence distribution of hyperlorenz chaotic system

由图2和图3可知，经微小改动后的初始值代入混沌发生器，由于超混沌特性会产生无规则无周期性变化的序列，因此初始状态和少量参数的变化就可以产生满足密码学基本特征的混沌源序列。

3 Strcmp序列分解算法设计

3.1 数理命题逻辑运算与位运算

命题逻辑研究以命题为基本单位，利用逻辑运算符和推理规则对命题进行演算，进而求出其真值[8]。

首先使用一个形式符号P表示在描述位置上有一个命题，称该变量获得指派，此时变量取得真假值。通常用1表示为真，用0表示为假。因此在具体的复合命题当中，需要引进所谓的命题联词以描述原子命题及其构造关系。将真假值与二进制序列组相结合，其中任意二进制序列按照每2位分割有4种可能情况：00，01,10和11。对传统的逻辑运算略作修改使其满足加密使用的二进制序列运算法则，且保证命题联词具有严格的逻辑含义，以及符号系统的语义与其原有自然系统语义的一致性。本文所讨论的联词包括合取词(∧)、析取词(∨)、蕴涵词(→)和等价词(↔)，并规定了其明确的运算规则，如表1所示。

Table 1 Truth table of mathematical propositional logic

其中，命题的合取式p∧q规则：p与q同时为真时才真，其余为假；命题的析取式p∨q规则：p与q同时为假时才假，其余为真；命题的蕴涵式p→q规则：p与q互异时为真，相同时为假；命题的等价式p↔q规则：p与q同时为真或同时为假时才真。

3.2 Strcmp序列分解规则

以数理复合命题逻辑真值表逆运算为基础，利用其逆运算对二进制分解源序列按照选取的运算规则与00，01，10，11做Strcmp对比，具体流程如图4所示，最后将分解的序列排列为一维向量作为加密源序列。

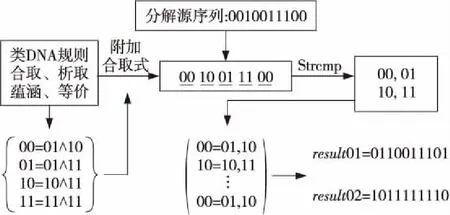
Figure 4 Schematic diagram of Strcmp sequence decomposition

假设选取的合取式为表1中编号为3,6,9,10的逆运算组成合取分解规则，则可以将序列0110110011分解为：

result01=0110110011

result02=0111111011

若是选取表1中编号为2,6,9,10的逆运算组成合取分解规则，则会错误地把序列0110110011分解为：

result01=0110110011

result02=0111110111

由于混沌初值的敏感性，且Strcmp分解规则的选取可作为密钥，会使得系统安全性得到很大提升。

4 加密算法

本文设计了一个具有密文熵反馈机制的混沌发生器，附加Strcmp分解规则的加密算法，利用反馈重置产生的序列分别对图像块进行加密，整体流程如图5所示。

Figure 5 Overall image encryption algorithm

假定明文图像大小为M*N。

Step1预处理分块。

对明文图像进行灰度转换后按2*2均匀分块，依次得到明文A、B、C、D块，各块大小变为M/2*N/2。

Step2产生混沌序列。

设置混沌发生器，采用龙格-库塔法(Runge-Kutta)[9]对超Lorenz混沌离散化处理后进行求解，产生4个序列X、Y、Z、W，并制定密文熵反馈机制：即代入原始初值产生混沌序列并利用序列X做分解得到result11和result12,对原文A块进行置乱和扩散加密得到密文A′块；再使密文A′的熵值H(其计算如式(3)所示)作为混沌发生器新初值，利用新初值产生的混沌序列Y做分解得到新序列result11和result12,用新序列加密原文B块；同理根据密文熵反馈机制对图像各块依次完成加密。

(3)

其中,L为图像的灰度随机等级数；p(i)为灰度值i出现的概率。

在调用混沌序列时每3 000次利用式(4)对混沌状态进行1次扰动，h为扰动项系数。

(4)

并对混沌系统本身产生的序列值s进行限定预处理，使之由浮点数类型的伪随机序列生成整数类型的伪随机序列S，长度为2*M/2*N/2，即:

S=mod(floor(s*pow2(16)),256)

(5)

最后经过式(6)得到的向量Z就是要分解的源序列:

Z=reshape(dec2bin(S),1,

2*M/2*N/2*8)

(6)

Step3选取分解规则。

从真值表中选取4式分解规则，对密文熵反馈后混沌发生器产生的序列进行分解。

Step4混沌序列分解。

对各块密文熵反馈得到的混沌序列值经式(5)限定处理后，分别进行序列X合取分解、序列Y析取分解、序列Z蕴涵分解、序列W等价分解，按照分解算法每两位一组，做循环分解i=1:k，其中k=length(Z)/2-1。

最后利用式(7)得到加密序列，其中M和N为图像的长和宽,a1和b1为分解项。

(7)

Step5图像置乱及扩散。

利用分解得到加密序列对各图像块进行置乱和扩散，result11用于置乱操作,result12用于扩散操作，最终得到密文块A′、B′、C′、D′。

置乱部分：

序列分解完成后，利用result11序列对块进行伪随机矩阵优化Anorld置乱[10]；将明文图像展开为一维向量，记为A，大小为M*N*1，对向量A的任一点坐标位置(1,j)进行Anorld变换，得到新的坐标位置(p,q)，如式(8)所示:

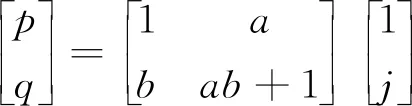
(8)

利用式(8)可通过伪随机变量a和b实现像素点(1,j)和(1,q)之间的变换，同时，将a*b+1视为一个新的随机数，记为a′。

扩散部分：

利用result12序列按照式(9)对块进行加取模扩散[11]:

Ci=(Ci-1+Si+Pi) mod 256

(9)

其中，原始明文图像被展开为一维向量P，相应的密文也为一维向量C，S为密码向量，i=1,2,…,M*N，i=0时初始值C0来自密钥。

将分解产生的序列分别保存到正向算法和逆向算法的伪随机向量中，如式(10)所示:

(10)

加取模循环2次使得任意明文像素点信息扩散到整个密文图像中。正向(按i从1到M*N)的算法与其逆算法分别如式(11)和式(12)所示：

Ci=(Ci-1+Si+Pi) mod 256

(11)

Pi=(2*256+Ci-Ci-1-Si) mod 256

(12)

逆向(按i从M*N到1)的算法与其逆算法分别如式(13)和式(14)所示：

Ci=(Ci+1+Si+Pi) mod 256

(13)

Pi=(2*256+Ci-Ci+1-Si) mod 256

(14)

Step6合块密文。

将利用序列分解后加密得到的密文块按照分块顺序合并，得到最终密文图。

解密为加密的逆运算，即对密文图分块,将原始初值代入混沌系统，利用Strcmp分解规则对产生的序列进行分解后再对A块加密，计算A′熵值后，代入密文熵反馈机制产生混沌序列，依次对各分块进行解密后合并得到原文。

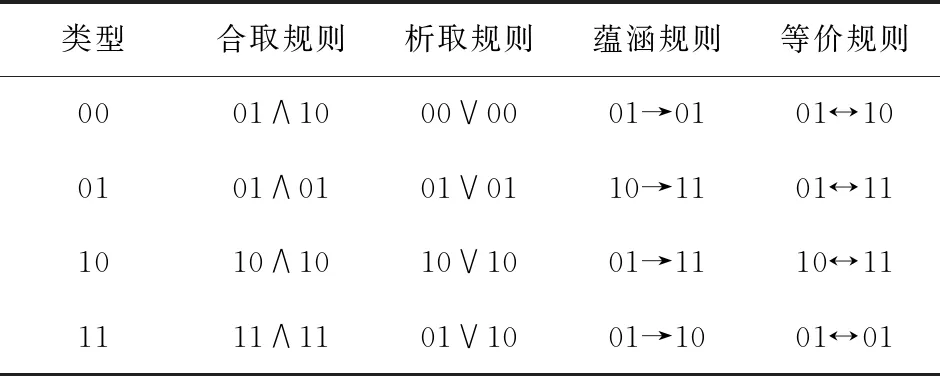
Table 2 Decomposition rules selected by this paper

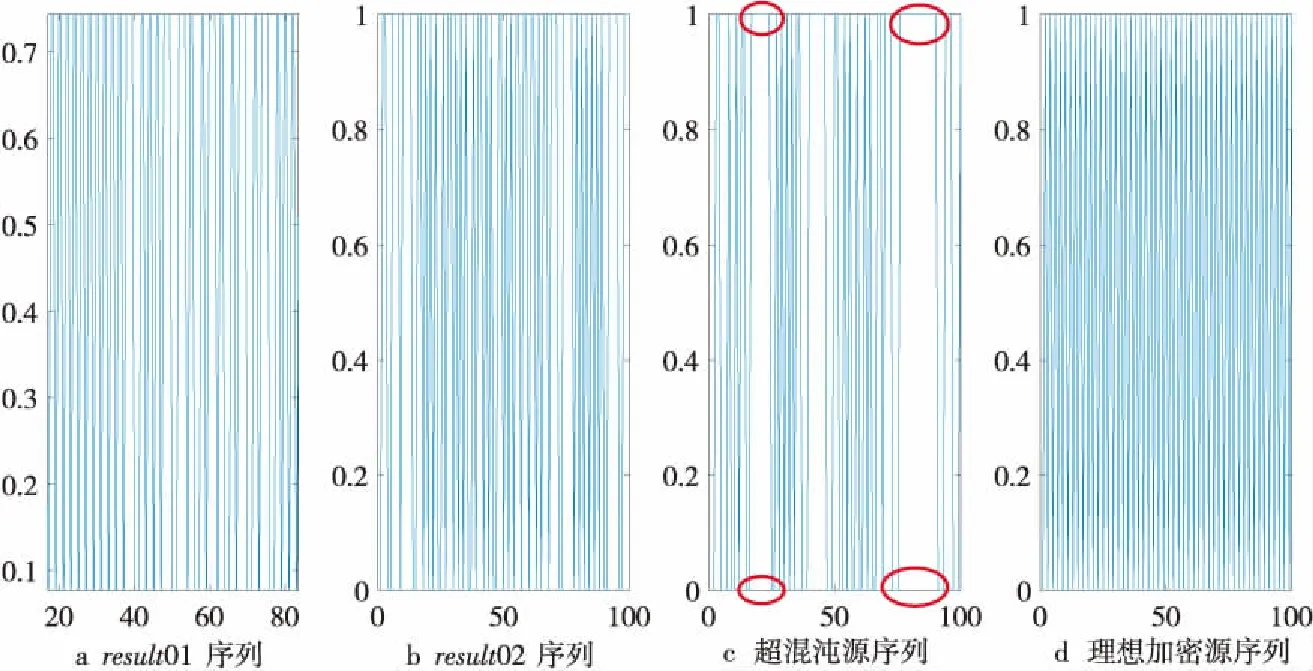
Figure 9 Detection diagram of sequence run-time distribution

5 实验仿真及安全性分析

5.1 实验仿真

在64位Windows 10操作系统、4 GB内存及Matlab 2016a环境中进行仿真实验。选取大小为512*512的Lena、Pepper和Ape图像作为明文，利用表2分解规则得到的结果分别如图6～图8所示。

Figure 6 Encryption effect of Lena

Figure 7 Encryption effect of Pepper

Figure 8 Encryption effect of Ape

5.2 安全性分析

5.2.1 分解序列均匀性检验

对序列作游程随机分布检验，即检测分解序列局部分布值，理想状态下0和1的分布不宜过多，也不宜过少，理论占比为50%，如式(15)所示，结合二进制的运算机制才能产生较好的加密序列值[12]。

(15)

其中，U为局部序列中0和1的总个数，π(i)(i=0,1)为序列中i所占个数。从分解序列中随机选取100位序列值作游程性随机分布图，由图9可知，不经过序列分解的混沌序列值(图9c椭圆形标出部分)分布不均匀，而经过Strcmp分解得到的加密源序列更接近期望图分布图。

5.2.2 直方图分析

直方图可直观地显示出图像像素点大小所占比重，对比图10～图12所示原文灰度直方图和密文灰度直方图可知，加密后图像像素值整体平稳且于像素区间均匀分布，可认为经加密得到的密文能很好地抵抗统计分析攻击。

Figure 10 Text-ciphertext histogram of Lena

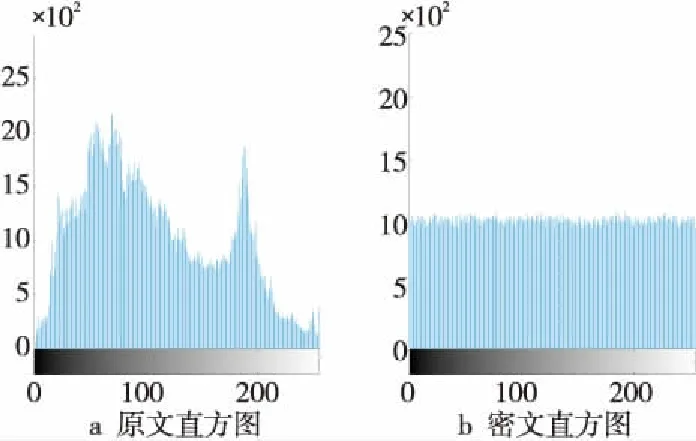
Figure 11 Text-ciphertext histogram of Pepper

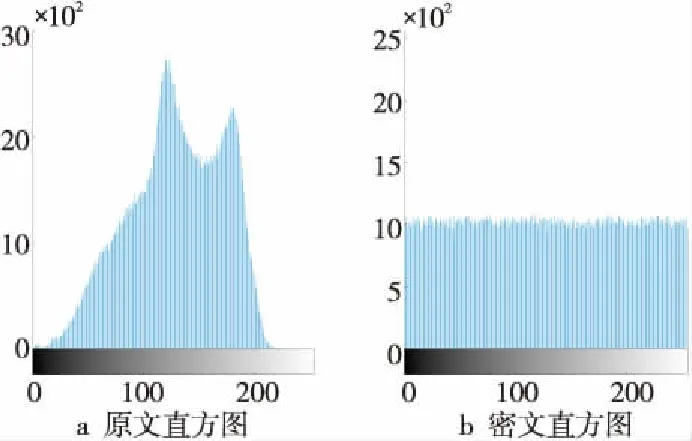
Figure 12 Text-ciphertext histogram of Ape

5.2.3 相邻像素相关性分析

明文图像具有较强的相关性，相邻像素点大多在水平、垂直、正对角和反对角方向上，有效的加密算法会大大降低其相关性，使得其相关系数趋近0。令一小块中的像素集合为“相邻像素点”，在理想状态下，应该将相邻的像素点尽可能地分散开，使得相邻像素点间相关性降低[13]。从图像中任取G对相邻像素点，则他们的灰度值为(ui,vi)，i=1,…,G,则向量u={ui}，v={vi} 的相关系数定义如式(16)所示：

(16)

其中cov(u,v),D(u)和E(u)分表代表协方差、方差和平均值。

本文分别随机选取4 000个明文和密文的相邻像素点通过式(16)，对明文和密文图像中3个不同方向的相邻像素相关性进行对比分析，分析结果如图13和图14所示。

从明文相邻像素相关性分布图中可知，明文图像相邻像素间具有很强的线性关系；而由密文相邻像素相关性分布图可知，其各个方向上皆无相关性，且像素点分布较为均匀。

利用式(17)可以计算出明密文相邻像素水平、垂直、正反对角方向上的相关系数。

(17)

5.2.4 信息熵

信息熵是衡量随机性的重要标准，其计算方式如式(3)所示，理论上，灰度随机图像在理想状况下的信息熵应该为8。

表3列出了Lena、Pepper和Ape图像的信息熵以及与不同方法之间的比较结果，可以看出经过加密算法得到的测试对象熵值均接近理论值，能够有效抵抗信息熵攻击。

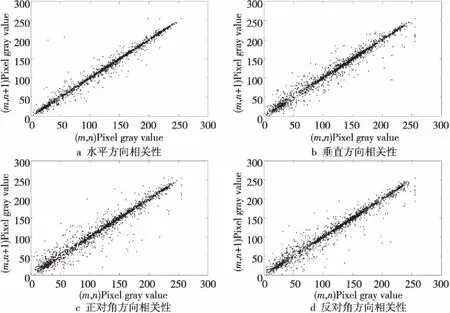
Figure 13 Correlation diagram of adjacent pixels of Lena plaintext image

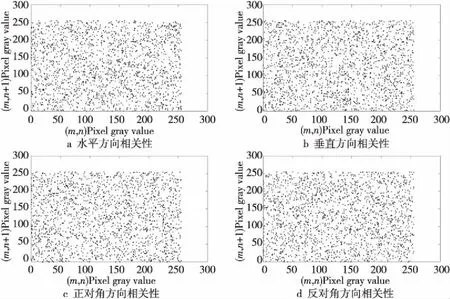
Figure 14 Correlation diagram of adjacent pixels of Lena ciphertext image

5.2.5 抗差分攻击分析

为了抵抗差分攻击，加密算法需要对明文图像高度敏感，即稍微改变明文图像像素的任何一位就能产生完全不同的密文图像。像素变化率(NPCR)和统一平均变化强度(UACI)可以衡量加

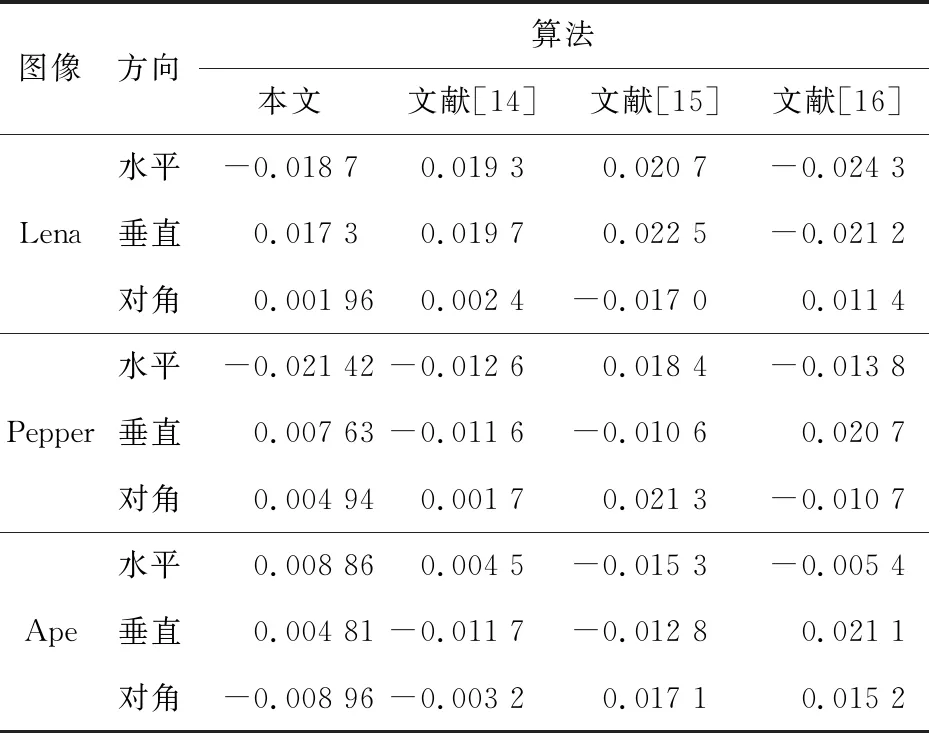
Table 3 Correlation coefficient relation test results of adjacent pixels

密算法对明文图像的敏感性。其定义分别如式(18)和式(19)所示:

(18)

(19)

(20)

其中，x(i,j)和x′(i,j)为改变像素值前后图像同一位置的像素点坐标，NPCR和UACI的期望值分别为 99.609 4%和 33.463 5%[17]。在分析测试中，随机改变Lena、Peppers和Ape中的1个像素值 ，得到的NPCR和UACI值如4表所示，其值均接近期望值，表明本文算法对明文图像具有较强的敏感性，可以有效抵制差分攻击。

5.2.6 选择明文攻击

选择明文攻击是传统密码攻击手段中最具威胁性的，因此对于已知明文攻击，攻击者可以通过加密一些特殊图像尝试找到加密密钥[18]。在本次测试中,选择大小为 512*512 的纯黑色和纯白色图像进行加密仿真，结果如图15所示，相应的信息熵和相关系数列于表5。由仿真模拟可得，实验数据均接近期望值，这表明无法从加密图像获得任何有用的信息，本文提出的加密算法对特殊图像可进行有效加密，且攻击者无法使用相同的密钥解密其他加密图像。因此，本文算法可以有效抵抗已知明文攻击和选择明文攻击。本次测试的时间复杂度如表5所示，良好的时间特性也可以体现出本文加密算法的优越性能。

Figure 15 Chosen plaintext attack test

6 结束语

本文将离散数学中的数理命题逻辑运算与混沌序列结合起来，并设定密文块熵值反馈交互机制，利用逻辑逆运算设计了Strcmp序列的分解规则，结合超Lorenz混沌系统提出了一种图像加密算法。对明文做分块处理后，将超混沌系统产生的序列进行分解，按照加密算法的设计对明文块分别加密，能够在减少时间冗余的情况下，进一步提高加密算法安全性。实验结果表明，该算法各项安全性分析值皆接近期望值，能抵抗常见密码学攻击，且对特殊图像加密效果较好。

未来将更进一步寻找设定新运算规则，从而与混沌序列中八位二进制的转化相结合，尽可能地使源序列更好地达到混沌序列的统计特性，以提出更高效的图像加密算法。

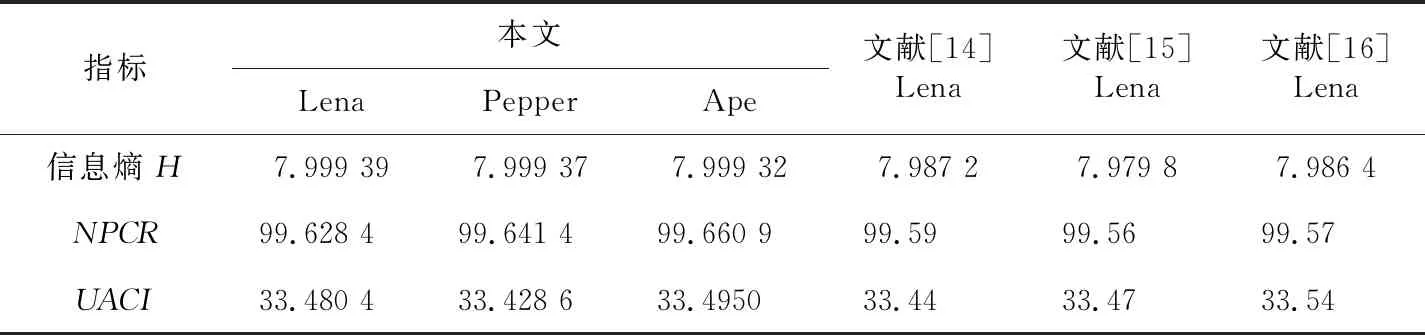
Table 4 Results of resistance to differential attack

Table 5 Analysis results of special images