基于广义变参Fibonacci混沌系统的压缩感知测量矩阵构造算法*
郭 媛,王 充,杜松英
(齐齐哈尔大学计算机与控制工程学院,黑龙江 齐齐哈尔 161006)
1 引言
压缩感知CS(Compressed Sensing)作为一种新的采样理论,在2004 年一经提出便引起了广大学者的兴趣,在很多领域被广泛应用[1,2]。CS理论改变了传统奈奎斯特(Nyquist)采样定理的采样方式,不以均匀步长方式对数据进行采样,采样频率远小于Nyquist的采样要求,在实现数据压缩的同时完成对数据的采样,降低了庞大采样数据量对数据处理的硬件和存储要求[3,4]。压缩感知理论主要包含:信号稀疏化表示、测量矩阵构造和重构算法3个方面[5,6]。其中测量矩阵的构造作为CS理论的关键环节,其构造矩阵的好坏直接决定了信号的重构精度和压缩程度。高斯随机测量矩阵、伯努利随机测量矩阵等随机矩阵[7,8]被证明以较高的概率满足有限等距特性RIP(Restricted Isometry Property)条件,常被用于测量矩阵的构造中。但是,随机矩阵的不确定性会造成实验结果的不稳定性,需大量实验取均值来消除影响;而且也会给数据的存储带来较大的压力,在实际硬件上的实现复杂度较高[6,9]。确定性测量矩阵也是常见的矩阵构造方式,在系统和参数固定时,测量矩阵也相应确定,解决了随机性测量矩阵带来的存储困难和实际硬件实现复杂等问题,吸引了广大学者的关注[10]。
混沌系统是一种复杂的非线性系统,具有内在的确定性和外在的随机性特征,常常被用来代替随机数应用于安全和保密方案中[11]。混沌性测量矩阵作为确定性测量矩阵构造的一种方式,因构造方式简单、矩阵元素具有伪随机性、重构性能较好,引起越来越多学者的重视[12]。2014年Gan等[13]利用Chebyshev 混沌系统构造测量矩阵,且给出了其满足RIP条件的证明,但矩阵的元素仍需间隔采样。2017年周伟等[14]提出了基于Logistic映射和Tent映射级联的复合混沌系统的测量矩阵构造,并验证了其可行性,但矩阵元素仍需间隔采样。2019年Ponuma等[15]提出了一种基于Chebyshev_Tent混沌映射的测量矩阵,并验证了其可行性,虽然不同混沌映射的级联减弱了数据之间的相关性,但仍需较小间隔的采样来满足数据统计的独立性。2018年Gan等[16]提出了一种基于多路T-way伯努利算法的伯努利混沌感知矩阵,并证明了其满足有限等距性质,但T-way伯努利移位系统依然采用简单的线性递推,相邻数据有较高相关性。
目前,混沌测量矩阵大多是基于一维混沌系统构造的,相邻数据之间的相关性较高,矩阵元素间隔采样的方式虽满足了数据统计的独立性,但也造成了数据资源的浪费。本文提出一种基于广义变参Fibonacci的混沌系统,相较于构造混沌映射间的级联来增大混沌系统复杂度,减弱数据相关性而言,本文提出的混沌系统在实现混沌映射级联的同时增加了不同混沌序列间的加性串扰,随机性和混沌性更强,混沌映射迭代产生的元素满足数据统计的独立性,用其构造的测量矩阵无需对采样间隔进行提前估计,提高了数据利用率。通过实验仿真,验证了其可行性和高效性。
2 CS理论
压缩感知是利用信号稀疏性进行信号重构的技术,被测量信号可稀疏化是压缩感知理论的前提[1 - 6]。其表达式为:
(1)
其中,x∈RN为一维离散信号,N为信号长度,ψ=[ψ1,ψ2,…,ψN]为一组向量正交基,θ∈RN×1为信号x在正交基上的展开系数,若θ中仅存在k个非零系数,则称信号x是可稀疏化的[5,6]。对可稀疏化信号x,将其投影到另一组测量向量基φ=[φ1,φ2,…,φM]T上,得到x的M个线性测量值[5,6],即:
y=φψθ=Aθ
(2)
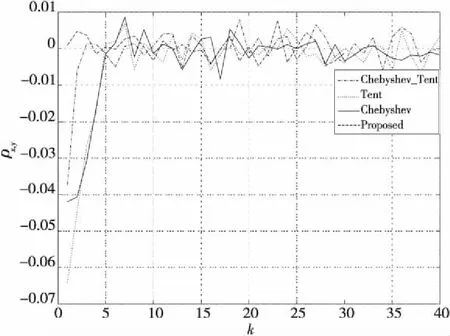
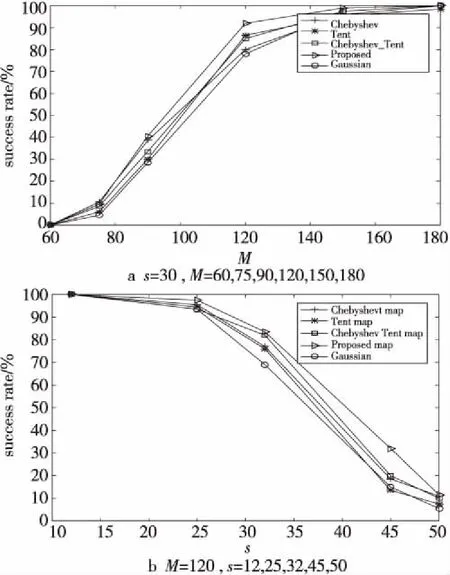
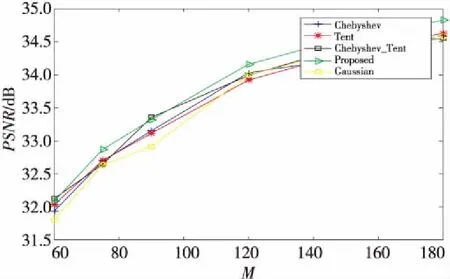
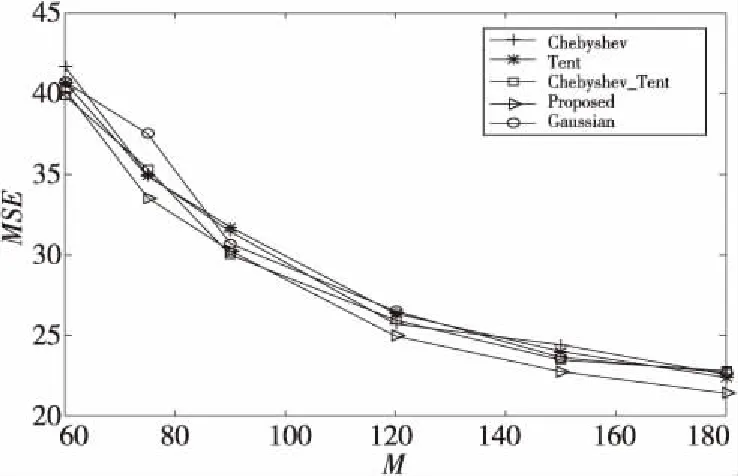
其中,矩阵y为压缩后的测量值,A=φψ为M×N的感知矩阵,因矩阵维度M< (3) 则从测量值y中重构出信号的稀疏系数θ可以转化为L0的范数优化问题: s.t. ‖y-Aθ‖2≤δ (4) 其中,δk为0~1的常数,δ为最小的δk。 混沌系统作为对初值和控制参数高度敏感的复杂非线性系统,也是不可预测的、伪随机的和遍历的[17]。本文级联量子Logistic混沌系统和Fibonacci数列构造广义变参Fibonacci混沌系统,其定义为: Fi=(AFi-1+α1BFi-2+α2CFi-3) modD (5) 其中,A,B,C为3个系数;α1,α2为权值系数;Fi为迭代的Fibonacci数列;D为常数。混沌系统模型通过级联的方式,将量子Logistic混沌的不同序列用Fibonacci数列串扰在一起,降低了序列元素的相关性,增强了混沌映射的随机性。 其中量子Logistic作为一种多维混沌系统,在混沌迭代的同时增加了扰动修正,在迭代过程中不断更新,混沌序列的非周期性更好,混沌的伪随机性更强。其混沌映射的表达式为: (6) 为平衡量子Logistic不同迭代序列在串扰中的强度,本文根据xi,yi,zi各自组成的序列x,y,z的遍历范围设置权值系数。在可调参数γ=3.99,耗散参数β=6.2,xi,yi,zi初始值均为0.1,系统处于较好的混沌状态时,此时不同序列的遍历空间为x∈[0,1],y∈[0,8e-5],z∈[-0.01,0],将所有序列的遍历空间统一扩充到相同大小时,权值系数设置为α1=1.25e+4,α2=100。 序列分布图和直方图能直观地反映混沌系统的序列迭代变化和分布均匀性,本文将式(5)迭代5 000次,舍去前500次的结果,来产生均匀非相关混沌序列,并将其与Logistic混沌映射相比,结果如图1所示。 Figure 1 Comparison of sequence distribution and histogram of chaotic systems 从图1可以看出,本文构造的广义变参Fibonacci混沌系统有更好的遍历性和随机性,比传统Logistic映射序列分布更均匀。 信息熵量化了数据的分布和混沌序列的随机性,信息熵值越大,表示系统的混沌性越强,数据随机性越好,信息熵定义为[18]: (7) 其中,Pr(mi)为灰度值mi出现的概率,U为图像的灰度等级数(通常为256)。随机统计500 000组数据,对Chebyshev映射、Tent映射和基于Chebyshev_Tent映射进行对比分析,区间统计数分别为256,500和1 000时,信息熵定量分析如表1所示。 Table 1 Comparison of information entropy 由表1可见,在对比的4种混沌映射中一维Tent映射和Chebyshev映射的信息熵较小,而基于Chebyshev_Tent级联映射的混沌复杂度变高,信息熵也变大;本文构造的广义变参Fibonacci混沌映射信息熵最大,与该统计区间能达到的最大信息熵相近。可见本文构造的混沌系统随机性更强,混沌性能更好。 图2为Chebyshev映射、Tent映射、Chebyshev-Tent映射混沌系统迭代序列Xn与Xn+1的关系及本文提出的广义变参Fibonacci映射的混沌系统的迭代序列Fn与Fn+1的相空间特性对比。 Figure 2 Phase space characteristic diagram of chaotic systems 由图2可见,在对比的4种混沌映射中,一维Chebyshev映射和Tent映射为简单线性递推函数,相邻数据线性关系明显;Chebyshev_Tent混沌映射虽然提高了系统的复杂性,但从相空间特性图中依然可以看到规律。本文提出的混沌系统,因系统参数随迭代而不断变化,相邻数据之间不存在明显线性关系,空间特性也无规律可循。图2表明本文所构造的混沌系统产生的序列相关性较小,更适合混沌测量矩阵的构造。 为降低数据间的相关性,使矩阵元素满足独立性,序列往往采用间隔采样的选取方式。皮尔逊相关系数法常被用来评估混沌序列的采样间隔。皮尔逊相关系数ρx,y定义如下: (8) 先生成10 000个模拟正态分布的数据,这组数据不相关且相互独立。通过混沌系统的迭代生成2组数据,初始迭代次数为200次,2组数据迭代间隔为k,得到2组结果分别记为变量X,Y;在不同采样间隔时,变量X,Y的相关系数如图3所示。 Figure 3 Comparison of Pearson correlation coefficients 由图3可见,Tent映射和Chebyshev映射初始相关系数较大,即不间隔采样的混沌映射,相邻数据间的相关性较强;随着采样间隔的不断增大,相关系数逐渐趋于区间[-0.01,0.01]。级联的混沌映射虽然较快收敛于区间,但仍需间隔采样。本文提出的混沌映射,相关系数从初始值开始就较小。以0.01为阈值,相关系数小于阈值的2组数据满足不相关性,可以看出本文构造的混沌映射满足数据统计的独立性。 针对一维混沌测量矩阵的不足,本文提出基于广义Fibonacci的混沌系统,具有较强的混沌特性且序列分布更加均匀,相邻序列元素间相关性低,极大概率满足测量矩阵的非限性等距条件。基于此本文构造了一种新的测量矩阵算法,测量矩阵的混沌特性更强,矩阵列的相关系数更低,压缩程度更高,系统重构效果更好,具体构造方式如下所示: (1)给定量子Logistic混沌系统的初始参数x0=y0=z0=0.1,控制参数γ=3.99,β=6.2。迭代混沌系统产生3组混沌序列作为广义Fibonacci混沌系统的权值参数。 (2)广义变参Fibonacci系统的初始参数F1=F2=F3=0.8,为平衡不同序列间的串扰强度,给定参数α1=1.25e+4,α2=100。 (3)不断按式(6)迭代混沌序列,产生一组长度为M×N的序列V={V0,…,Vn,…,VMN-1}。 (4)将生成的序列V按列进行排序,构造M×N大小的测量矩阵Φ,矩阵的表达形式如下所示: (9) 常用其他混沌系统因序列元素不满足数据统计的独立性,需对混沌产生序列元素按采样间隔k进行重新采样,得到大小为M×N的序列,初始产生的混沌序列长度最小为M×N×k。本文提出的测量矩阵和其他几种测量矩阵对比情况如表2所示。 Table 2 Comparison of data utilization ratio 表2直观反映了本文提出的算法对数据的利用率达到1,而其他测量矩阵计算量是本文矩阵的k倍,数据利用率仅为1/k,具体利用率由矩阵的采样间隔来决定。 测量矩阵构造的首要问题为矩阵是否满足RIP特性条件。Baraniuk 等[19]通过Johnson-Lindenstrauss 引理给出了随机矩阵满足RIP特性的证明。设随机矩阵U∈RM×N,存在常数δk∈(0,1),矩阵能以很高的概率满足 RIP 特性: (10) 具体表述为,当测量值M>(c0k·ln(N/k)),随机测量矩阵满足 RIP 特性条件的概率为: (11) (12) Zhang等[18,20,21]给出了由混沌测量矩阵构造的伪随机矩阵,在矩阵元素满足数据的独立性时,测量矩阵满足RIP条件的证明。在测量值M∈(k,N)时,存在常数c3>0,使得c4≤c(δ)-c3[1+(1+(lbs)/s)/lbN/s],其中,s为稀疏度,满足c4>0时,随机测量矩阵满足RIP特性的概率至少为: P≥1-2e-c4M (13) 本文在相关系数分析时证明了构造矩阵元素的数据满足统计的独立性,由此可以推出本文构造的测量矩阵能够以高概率满足RIP特性条件。 为验证本文基于广义变参Fibonacci混沌系统构造测量矩阵的有效性和可行性,本节分别对一维稀疏信号和二维图像的重构性能进行定量分析。分别选用Chebyshev混沌测量矩阵、Tent混沌测量矩阵、级联Chebyshev_Tent混沌测量矩阵和高斯混沌测量矩阵与本文提出的混沌测量矩阵进行比较,以说明本文测量矩阵构造算法的可行性。 本文在Matlab环境下随机生成了一维离散稀疏信号,采用经典正交追踪算法OMP(Orthogonal Matching Pursuit)对随机信号进行重构。通过对信号的重构成功率和重构误差进行定量分析,来验证所构造测量矩阵的性能,并与多种常用的测量矩阵的重构效果进行比较。 重构成功率的统计方法为通过正交追踪的重构算法进行迭代重构,当迭代截止时的残差值|r|<1e-6时,测量值与重构信号之间的误差足够小,则认为信号重构成功,即: (14) 信号的稀疏度和测量次数作为影响信号的重构成功率的关键因素。设信号长度N=256,在固定信号稀疏度时,测试不同测量值下各测量矩阵的重构成功率;同时测试测量次数固定,在不同稀疏度下各测量矩阵的重构成功率。其中,固定稀疏度s=30时,测量M分别取值60,75,90,120,150,180;固定M=120时,s分别取值12,25,32,45,50。为消除随机性对实验结果的影响,同一稀疏实验重复进行200次,取信号重构成功率的均值如图4所示。 从图4a和图4b可以看出各测量矩阵的重构成功率的曲线图基本一致,且随着测量值M的逐渐增大或信号稀疏度的逐渐减小,重构成功率都在不断提高,在测量值M>120或信号稀疏度s<25时,测量矩阵都能以大概率实现信号的精确重构。但是,从测量值M>75开始,本文算法的测量矩阵的重构成功率比其他测量矩阵的高,在M=120,即采样率接近1/2时,重构成功率高于较好的Tent映射(4%),随着测量值的不断增大,重构成功率最先接近100%。 为了对各测量矩阵的重构性能差异精确比较,重复200次实验取均值,对几种测量矩阵在不同测量值下的重构误差进行了定量分析,如表3所示。 Figure 4 Comparison of the reconstruction success rate Table 3 Comparison of reconstruction errors under different measurement M 由表3可见,比较其他测量矩阵,在不同测量值下,本文构造的测量矩阵重构误差均能达到最小,表明本文构造的测量矩阵在不同采样率下,均能有很好的重构效果,系统整体稳定性较好。 本文选取256×256的Lena图像,将其分割成16×16的图像块,通过离散余弦变化对图像进行稀疏化处理,利用OMP算法对图像进行重构,其中测量矩阵选取Chebyshev混沌矩阵、Tent混沌矩阵、基于级联的Chebyshev_Tent混沌矩阵、本文所提出的混沌矩阵和随机高斯测量矩阵。为定量分析不同测量矩阵对Lena图像的重构性能,以图像信噪比和图像均方差作为评价指标。 图像信噪比定义如下: PSNR=10×lg (2552/MSE) (15) 其中MSE表示原图像与重构图像均方差,定义如下: (16) 从图5可见,相同采样率时,一维Chebyshev测量矩阵、Tent测量矩阵和级联Chebyshev_Tent测量矩阵均与随机高斯测量矩阵的重构信噪比相近,本文所提出的测量矩阵的重构所得信噪比略高于其他测量矩阵的。以测量值M=120,即采样率接近1/2为例,本文测量矩阵重构信噪比高出其他较优的测量矩阵(0.2 dB);随着采样率的不断增大,本文提出的测量矩阵的重构信噪比也越高。从图6中可以看出,不同采样率时,本文提出的测量矩阵的重构均方差曲线均在图像最下方,表明本文提出的测量矩阵重构均方差最小,重构效果最优。 Figure 5 PSNR comparison Figure 6 MSE comparison 为直观观测图像的重构效果,在采样率M/N接近1/2,即测量值M=120时,5种不同测量矩阵重构图像如图7所示。 Figure 7 Comparison of reconstruction effects of Lena image 由图7可见,和其他混沌测量矩阵比较,本文提出测量矩阵的整体重构效果最优,所得图像清晰度高于其他图像,能实现较好的重构效果;且在帽子和眼睛等图像纹理复杂区域本文算法恢复得更好。 当前基于混沌系统的测量矩阵构造多依托于一维混沌系统,序列元素相关性较强,构造测量矩阵时需间隔采样来满足数据统计的独立性,造成数据资源的浪费。本文通过级联量子Logistic混沌和Fibonacci数列构造了广义变参Fibonacci混沌系统,并与几种常用混沌测量矩阵构造系统,如一维Chebyshev混沌系统、Tent混沌系统和基于两者级联的复杂混沌系统相对比,在混沌特性和重构性能上进行定量分析。一维稀疏信号采样率为1/2时,本文算法构造的矩阵的信号重构成功率高出其他矩阵4%;二维Lena图像的重构实验中,采样率为1/2时,本文算法构造的矩阵的重构信噪比高出其他测量矩阵0.2 dB。且本文构造的测量矩阵无需对采样间隔进行提前估计。
3 广义变参Fibonacci混沌测量矩阵
3.1 广义变参Fibonacci混沌系统构造
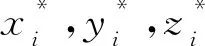

3.2 信息熵分析

3.3 相空间特性分析

3.4 相关系数分析
3.5 测量矩阵构造
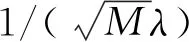

4 实验与分析
4.1 一维稀疏信号
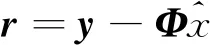
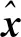

4.2 二维Lena图像


5 结束语

