怎么做才能快速找到最大公因数
□吴 霞
最大公因数是学生进一步学习约分和通分以及分数四则混合运算的基础。怎么做才能让学生快速找到最大公因数?教师可设计如下教学活动。
一、创设情境,设疑引入
教师依次出示5 张数字卡片:3,4,6,8,16。男、女生各推荐一人,男生抢12 的因数,女生抢16的因数,抢卡片多的一方获胜。
引导思考:你们知道取胜的关键是什么吗?为什么?
二、自主学习,抽象概念
(一)自主研究
请学生用自己喜欢的方法找出12 和16 的因数。
(二)展示重点
为了更直观、形象地抽象出公因数和最大公因数的概念,教师有针对性地用集合图的形式展示方法(如图1)。

(三)比较感知
学生通过比较,直观地得出:3,6,12是12独有的因数;8,16是16独有的因数;1,2,4是12和16公有的因数,其中4 最大,故4 是12 和16 的最大公因数。
(四)抽象概念
学生在类比中抽象出公因数和最大公因数的概念。
三、合作交流,探寻方法
(一)激趣表演
请学号为1,2,3,6,9,18,27的同学上台表演。学号是18 的因数的同学站在左边,学号是27 的因数的同学站在右边,学号是18 和27 的公因数的同学站在中间。通过表演,学生很快找出了18 和27的最大公因数是9。
(二)探寻方法
通过小组的交流、反馈,得出以下找最大公因数的方法。
1.列举法。
18的因数:1,2,3,6,9,18;
27的因数:1,3,9,27;
18和27的公因数:1,3,9,其中9最大,故18和27的最大公因数是9。
2.筛选法。
先看18 的因数有1,2,3,6,9,18,再看18 的因数中哪些是27 的因数,即1,3,9 是27 的因数,9 最大,故18和27的最大公因数是9。
3.分解质因数法。
18=2×3×3;
27=3×3×3;
18和27的最大公因数是3×3=9。
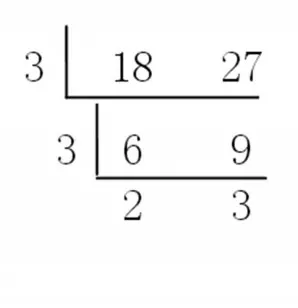
4.短除法。
18和27的最大公因数=3×3=9。
四、异中求同,渗透思想
无论采用哪种方法,都要遵循找“因数—公因数—最大公因数”的流程。
综观整个过程,教师让学生在自主探究中建立概念、理解概念、探寻方法,充分体现了以“学生为主体,教师为主导”的教学理念,努力追求学生个性的自然发展,渗透解决问题多样化的数学思想。

