大型客机后缘铰链襟翼巡航变弯度气动性能数值研究
夏 慧 刘沛清 戴佳骅 江润沛 张雅璇 栾博语 李庆辉
(北京航空航天大学,北京 100191)
0 引言
传统的増升装置主要在起、降阶段打开以增加飞机的升力,兼顾固定翼飞机的高、低速性。现代先进客机的增升装置被赋予更多功能,巡航变弯度技术便是其中一项[1]。固定翼飞行器的机翼在巡航阶段为固定外形,这种固定外形的机翼通常只针对一个设计点进行优化设计,即机翼在特定的巡航高度、速度和飞机重量下有最优的气动性能[2]。而实际飞行中,飞机在大部分时间都偏离了最佳设计点。此外,现代大型客机为保证飞机的安全性要求,飞机抖振升力系数应不小于巡航升力系数的1.3倍[3],在复杂多变的飞行环境下飞机很容易进入抖振。如果增加后缘襟翼偏转角度作为一个控制参数,可以改善飞机在不同飞行工况下的抖振边界。1972年,美国国家航空航天局研究了巡航变弯度技术在F104战斗机上的应用,该研究主要针对前/后缘襟翼的偏转对改善抖振边界的影响,其研究表明通过对前后缘增升装置在巡航阶段进行小角度的偏转能有效改善抖振边界,且后缘襟翼比前缘装置在提高升力及改善抖振边界等方面具有更好的效果[4]。随后的20世纪80年代,B.H.Lee等人[5]对后缘襟翼偏转改善机翼抖振特性进行了大量的实验研究,探究了襟翼偏转对跨声速区上翼面的流动及抖振边界的影响。同时,巡航变弯度技术也逐渐从军用飞机领域扩展到民用飞机领域。波音公司在1980年11月完成了机翼变弯度在商用运输类飞机上的潜在效益评估[6]。其研究结果表明:变弯度构型可提高飞机巡航阶段的气动效率,对于远程客机,可节约燃油3.1%以及减少约2%的直接运营费用。
综上所述,后缘襟翼的巡航变弯度设计主要有两大功能:(1)改善全航程的气动效率,提高燃油经济性;(2)抑制激波振荡,提高机翼跨声速抖振边界。本文对某大型飞机采用新型的下垂式后缘铰链襟翼,开展襟翼巡航变弯气动性能数值研究。
1 气动计算数值方法验证
1.1 稳态计算方法验证
目前的商用运输类飞机采用的翼型多属于超临界翼型,所以本文采用第二代超临界翼型SC(2)-0714进行二维定常数值方法验证,主要包括:网格无关性验证、不同求解器计算结果对比、不同湍流模型计算结果对比。得到各压力系数分布曲线与实验结果的对比。
1)网格无关性验证:采用了三套不同数量的网格见表1,计算条件为:来流马赫数为0.721,迎角为0.032°,参考NASA试验人员在兰利中心的跨声速低温风洞对SC(2)-0714翼型进行的二维试验结果[7],网格绘制采用CH远场,前后均50倍弦长,采用S-A湍流模型,y+为5。

表1 SC(2)-0714翼型网格无关性验证
SC(2)-0714采用的CH型网格,其拓扑结构如图1所示。

图1 SC(2)-0714远场与近壁面网格
由图2可见,三套不同网格数量对应的压力系数分布基本一致,均与试验结果相吻合。

图2 网格无关性验证压力系数分布
2)不同求解器计算结果对比,如图3所示,采用FLUENT和CFL3D两种求解器进行计算,两种求解器都能较准确地预测激波位置,压力系数分布均与实验值相吻合。
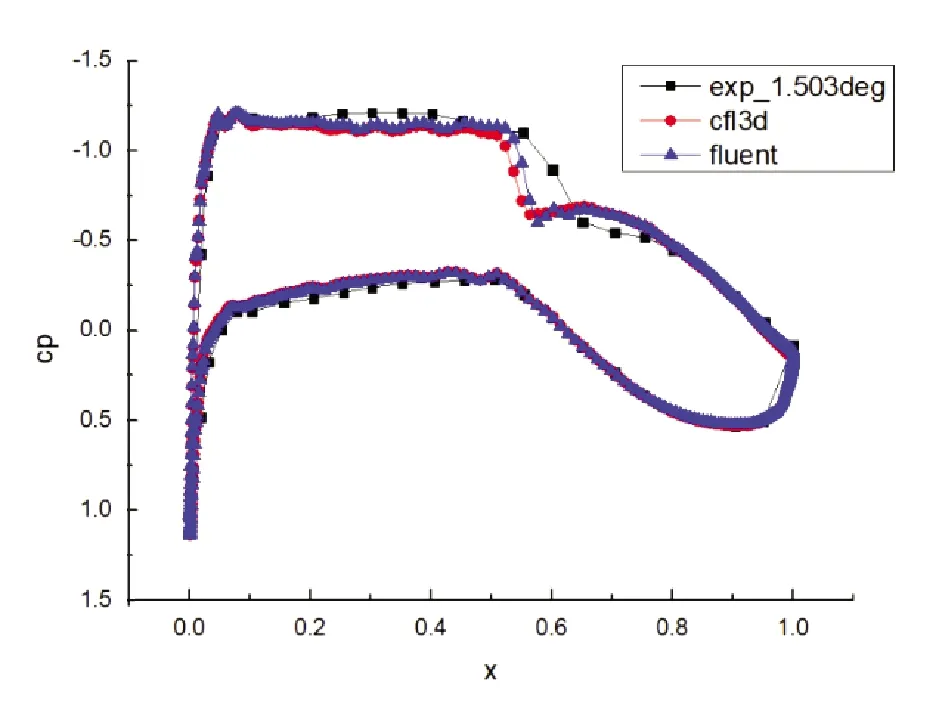
图3 不同求解器对压力系数的影响
3)不同湍流模型计算结果对比如图4所示,采用了S-A、k-ω SST、k-kl-ω三种湍流模型,计算结果显示,S-A模型和k-kl-ω模型均能较好地预测激波位置,压力系数分布与实验值相吻合。

图4 不同湍流模型计算结果对比
1.2 抖振边界预测的数值方法验证
OAT15A翼型有大量的抖振研究相关的风洞实验数据[8],该实验在法国航空航天研究中心S3Ch跨声速低温风洞中进行。该翼型广泛用于抖振边界预测的数值计算方法验证。该实验采用的来流马赫数为0.73,在迎角为3.5°开始发生较强的抖振和边界层分离。本小结主要进行了时间步长无关性验证和抖振边界预测准确性验证。网格拓扑结构、无界远场等与1.1小结一致,计算采用的来流马赫数为0.73,计算迎角为0°、1°、2°、3°、3.5°、4°,湍流模型采用S-A模型,二阶精度,时间步长为3.5 μs。
压力脉动均方根值(Cpmse)的计算公式如下:
(1)
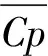
由图5、图6可见,时间步长对压力系数分布与压力脉动均方根值影响较小,且结果均与实验值较吻合。在后续的计算中,采用时间步长为3.5 μs。

图5 时间步长对翼型表面压力系数的影响

图6 时间步长对压力脉动均方根值的影响
抖振边界预测结果如图7与图8所示,从计算结果与风洞试验数据的时间平均压力系数分布对比可见,在激波位置的预测上,计算迎角比试验迎角大0.5°以内,并且可以看到从3°到3.5°再到4°有明显的激波位置前移,说明抖振发生在这个区间。同时,通过压力脉动的均方根曲线也可以看到,在0°、2°、3°的波动幅度都比较小,在3.5°时幅度陡增,也说明在这个区间发生了抖振。
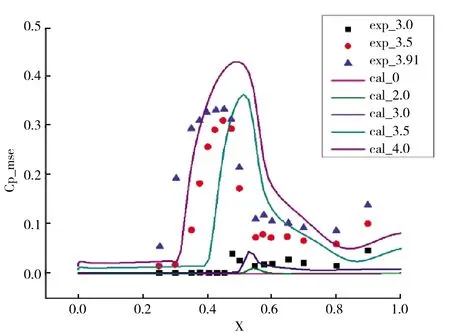
图7 计算与实验结果压力系数对比

图8 OAT15A上翼面的压力脉动均方根值曲线
2 铰链襟翼机构与扰流板联合偏转设计
传统的巡航变弯度优化设计通常是定轴偏转部分角度,再进行气动计算分析,并未考虑真实机构。本研究针对某宽体客机的先进后缘铰链襟翼,探究巡航变弯度在该飞机上的应用,利用数值计算方法评估对提高抖振边界和节省燃油经济性的影响。该大型飞机后缘增升装置使用的是大偏度顺气流下垂式铰链襟翼,这种襟翼机构的一个特点是襟翼的偏转为空间任意三维运动,并非单纯的定轴转动。所以其剖面巡航变弯度过程中并不是二维的定轴转动。在进行巡航变弯度设计时,本研究着重于三维机构引导下的二维剖面的巡航变弯度设计。
2.1 后缘襟翼机构运动形式
后缘铰链襟翼一般采用四连杆机构,新型的铰链襟翼可以与扰流板联合下偏,调整后缘襟翼与扰流板的缝道参数来获得更好的气动性能[9]。本次采用的机构布置方式外段襟翼采取RR4S-R5S的执行机构,如图9所示;内段襟翼为定轴旋转,而外段襟翼的运动较为复杂,其瞬时转轴在不断变化,并且还有沿轴向的平移。其中上标i表示内侧机构参数点,上标o表示外侧机构参数点,OA为主动杆,O点为主翼的后梁点,AB为连杆,DE和NE为襟翼的支撑杆,E点为固定铰支。图9中R表示转动副,S表示球面副。在起、降阶段,后缘襟翼偏转至对应的卡位,扰流板联合偏转,以获得最优缝道参数;在巡航阶段,襟翼可根据当前飞行状态偏转微小角度,同时扰流板联合偏转以密封上翼面,获得变弯度机翼的巡航构型。

图9 外段铰链襟翼机构示意图
2.2 襟翼与扰流板联合偏转程序流程
对后缘铰链襟翼机构进行求解,得到一套完整的、合理的机构参数之后,将这套机构参数作为输入,杆长及运动关系作为约束,编写襟翼与扰流板联合偏转的运动仿真程序。
首先,需要将巡航状态的襟翼及扰流板参数化,作为程序的一个输入文件。然后,对机构进行数学建模。利用机构运动关系,实现机构运动仿真程序的设计,通过不断的迭代,在扰流板与襟翼上翼面的距离满足要求时输出机翼对应的二维剖面。程序设计的流程如图10所示。
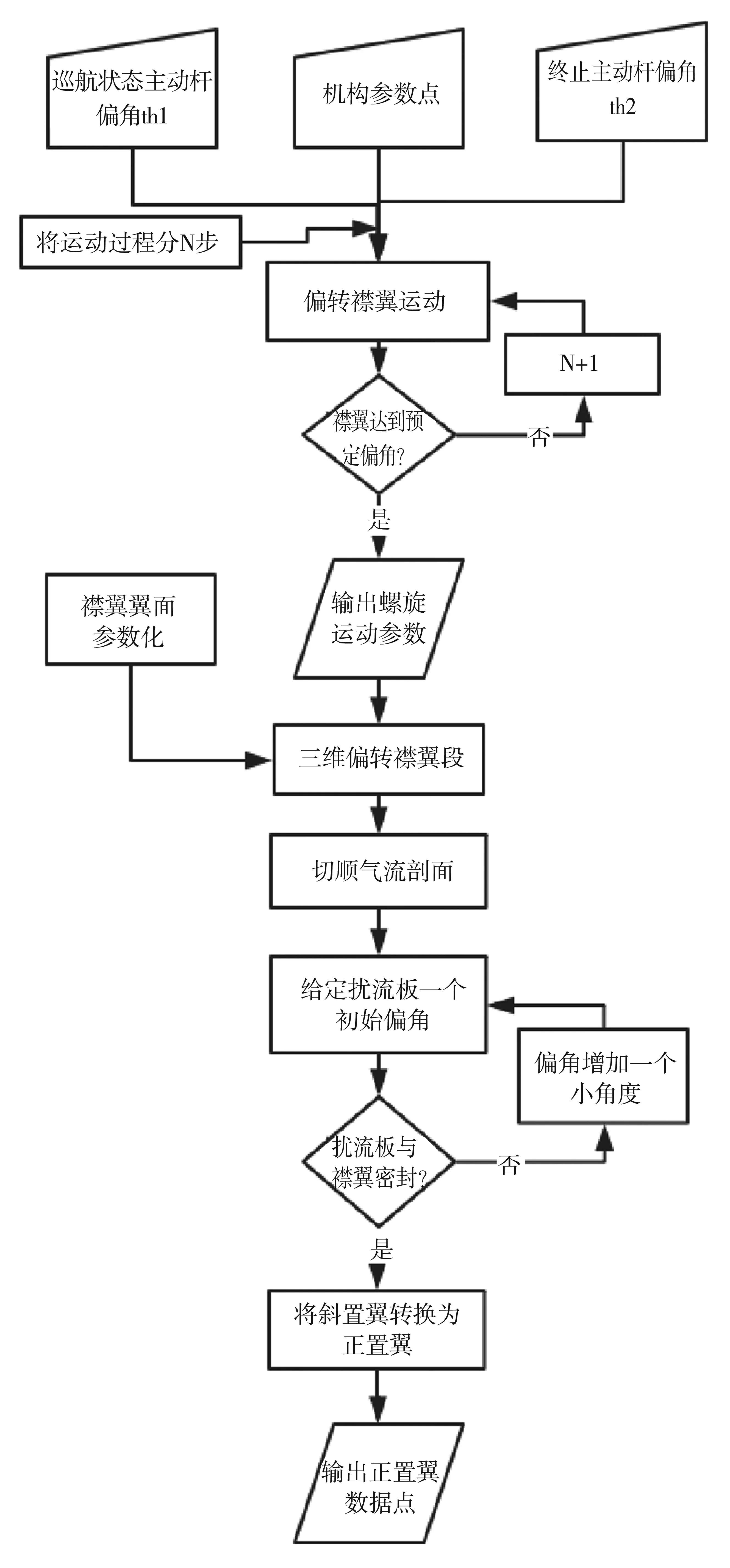
图10 襟翼联合扰流板偏转流程图
3 抖振边界及巡航气动效率计算
3.1 二维抖振边界预测
利用2.2节所述的程序,获得机翼kink处的正置翼型。计算环境为10 000 m高空,法向来流马赫数为0.717,干净弦长为5.456 8 m,第一层网格高度为5×10-6m。计算迎角为:0°、1.18°、2.37°、3.56°、4.15°、4.74°,扰流板与襟翼联合偏转示意图如图11所示。

图11 襟翼联合扰流板偏转示意图
1)不变弯度巡航构型的抖振边界预测。采用时间步长7 μs,总的计算时间为0.56 s,得到时间平均的压力系数分布图、压力脉动均方根曲线如图12和图13所示。从图12可以明显看出,在0°~2°时,压力脉动量均方根值几乎为0,在3°时开始有小的波动,在4°时波动陡增,进而计算3.5°迎角,可见在3.5°就已经有一个陡增。同时,通过图13可见,在3.5°时出现激波位置的前移,也说明抖阵发生在这个区间。
图14所示的时均流场图中可见,迎角从0°到4°,前缘吸力峰逐渐扩大,激波位置逐渐后移,在3.5°与4°时可观察到激波波脚处出现明显的流动分离,说明随着迎角的增大,尾缘流动分离区逐渐前移,激波逐渐后移,在3.5°时两者交叉,出现激波边界层干扰,与图12和图13对应的结果相符。
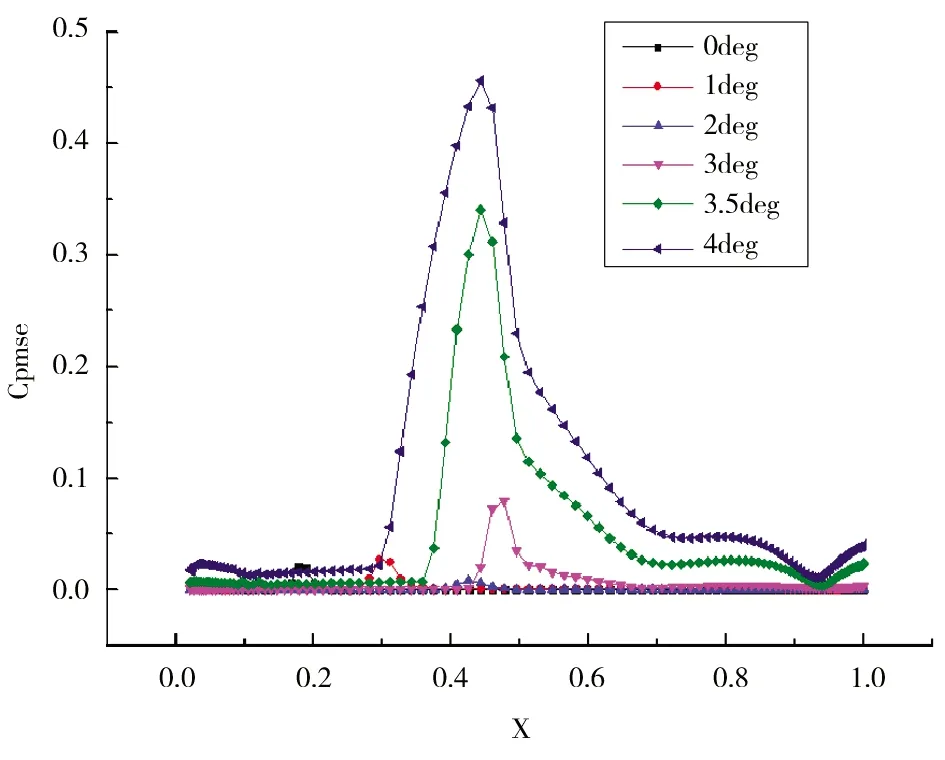
图12 原始巡航构型压力脉动均方根值曲线

图13 原始巡航构型的时均压力系数分布

(a)0° (b)1° (c)2°
2)后缘变弯度巡航构型的抖振边界预测。利用前文所述的预测抖振边界的方法,综合压力脉动均方根曲线出现陡增与时均压力系数分布曲线激波位置前移两种判据,表2展示了后缘襟翼偏转±1°、±2°、±3°对应的抖振边界预测结果,表中δ为襟翼偏角,抖振边界定义为抖振起始迎角,用α表示;其中襟翼偏角为正表示襟翼下偏,为负表示襟翼上偏。

表2 不同襟翼偏角对应的抖振边界
由表2可见,后缘襟翼每上偏1°,对应的抖振发生起始迎角约增加0.5°;襟翼每下偏1°对应的抖振发生起始迎角减小约0.5°,说明襟翼上偏具有良好的延缓抖振发生、提高抖振边界的作用;同时,由于襟翼下偏增加了机翼弯度,使得抖振起始迎角减小。图15和图16展示了襟翼偏角从下偏3°到上偏3°,迎角分别为3°和4°时上翼面的压力脉动均方根值曲线,可见上偏襟翼明显减小了上翼面的压力脉动幅值,襟翼下偏明显增大了该幅值。在3°迎角时,原始构型尚未进入抖振区,而在襟翼下偏1°、2°和3°时,对应的压力脉动均方根值曲线的幅值明显增大,下偏襟翼在3°迎角便开始发生了抖振。但在襟翼上偏的构型中,3°迎角的压力脉动幅值保持在较低的水平,无剧烈波动。接下来将利用流场图进一步说明襟翼上偏如何减弱上翼面压力脉动,从而扩大抖振起始迎角。

图15 压力脉动均方根值曲线(AOA=3°)
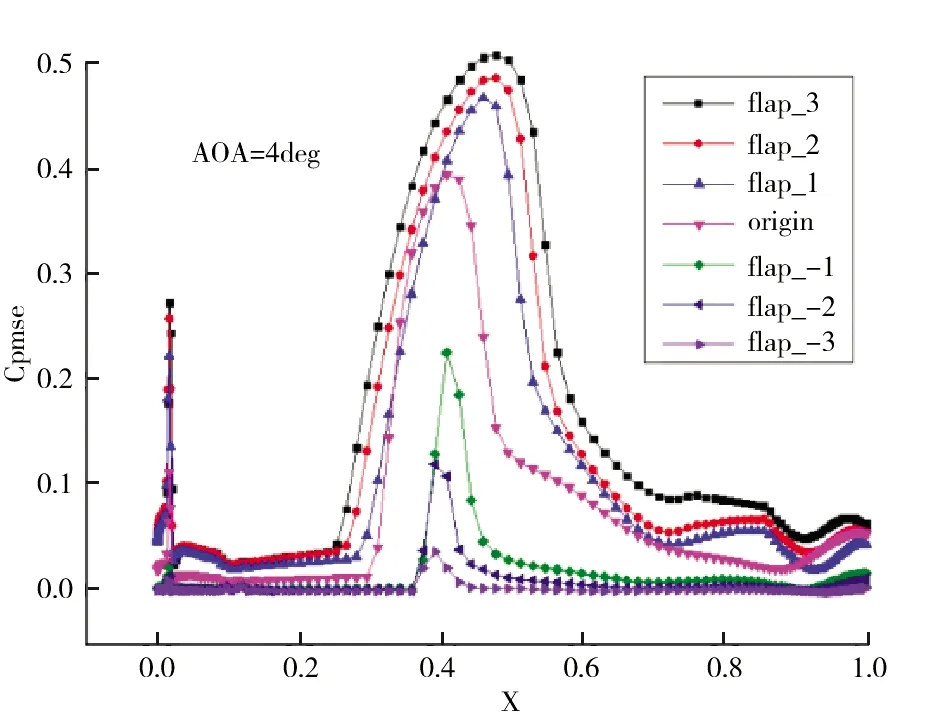
图16 压力脉动均方根值曲线(AOA=4°)
对于同一迎角(AOA=4°),图17与图18分别是襟翼上偏1°与上偏2°时一个周期内的时均流场图,可见在同一时刻,如0.14 s和0.28 s时,襟翼上偏2°减小了尾缘区的流动分离程度。根据前述判据襟翼上偏1°的抖振起始迎角为4°,在图17中亦可见明显的激波与流动分离区的位置在不同时刻的变化,在0.14 s时激波波脚分离泡与尾缘流动分离互相干扰,在0.28 s时干扰减弱,在0.42 s~0.56 s时尾缘流动分离区减弱甚至消失;与此同时,激波位置在前后不规则移动。而襟翼上偏2°时,根据前述判据,并未发生抖振,四个时刻的流场图也未见明显的流动分离与激波干扰现象。说明襟翼上偏可有效消除上翼面尾缘的流动分离。

(a)0.14 s (b)0.28 s

(a)0.14 s (b)0.28 s
3.2 巡航气动效率分析
利用本文2.2小节设计的机构与扰流板联合偏转的程序,自动生成不同襟翼偏角的翼型剖面,利用网格录制的方式自动绘制CH型结构网格,保证每一套网格都有相同的拓扑结构与网格数量;然后采用RANS方法计算气动力系数,采用S-A湍流模型,飞行条件为10 000 m高空对应的参数。襟翼偏转模型与角度均与3.1小节相同,每个襟翼偏角模型计算迎角范围为-2°~5°,间隔1°。将3.1小节得到的抖振边界作为约束条件,剔除超出抖振包线的点,得到图19。其中黑色实线(flap_0)表示原始固定翼构型的升阻比曲线,其上方玫红色的曲线(optimal)表示不同迎角、襟翼偏角对应的最优包络线。在相同的升力系数下,玫红色曲线对应的升阻比均大于原始构型的升阻比曲线。在飞机刚进入巡航阶段时,整机重量最大,所需的升力系数较大,此时可根据当前工况将襟翼下偏至对应角度,从而提高飞机的升阻比,达到当前飞行条件下的最佳气动效率。对于长航程飞机,在巡航阶段后期,其燃油消耗甚至可达机身重量的30%[10],此时可将襟翼上偏至对应的角度,从而减小升力系数,同时相比于原始构型,升阻比均有所增加。且本研究中可见抖振边界有所提高,因此有利于提高飞行速度。本文展示的是随着燃油消耗,整机重量不断减轻,通过连续调节襟翼与迎角的二维变弯度翼型气动计算结果,即二维理想情况下,在最优设计点附近,升阻比可提高约22.5%。同时,变弯度构型曲线的抖振边界相对于原始构型的抖振边界提高约10%。

图19 不同襟翼偏转构型的升阻比曲线
4 结论
本文首先进行了增升装置的机构与扰流板联合偏转的运动仿真程序设计,结合扰流板联合偏转技术,自动生成不同襟翼偏角的二维构型,并运用自动生成网格技术绘制结构网格。接着采用稳态与非稳态方法进行气动计算,分别用于全巡航过程气动效率计算与抖振边界预测。在抖振边界预测方面,采用了时均压力系数曲线上激波位置的前移与压力脉动均方根值曲线出现陡增作为抖振开始发生的判据,两种方法共同分析加强了抖振起始点判断的准确性。抖振边界预测的结果表明,襟翼上偏能有效提高翼型的抖振起始迎角,襟翼每上偏1°,约提高0.5°的抖振起始迎角。在气动效率方面,计算过程中保持马赫数不变,以升阻比为气动效率高低的判据。结果表明,巡航过程中,变弯度构型的升阻比大于或等于原始固定构型,抖振边界约提高10%。该结果为理想状态下连续调整襟翼与迎角后的二维翼型计算结果,表明巡航变弯度具有提高全航程气动效率的能力。

