大型客机柔性后缘增升装置气动机构一体化优化设计
张雅璇 刘沛清 夏 慧 戴佳骅 李庆辉 栾博语
(北京航空航天大学,北京 100191)
0 引言
增升装置设计技术的重大突破对进一步提高新一代民用客机的气动性能起着关键性作用,这在世界范围内也是一个很有挑战性的研究课题[1]。为了达到降低油耗、减少噪声和污染的目标,高效航空发动机技术、复合材料机身、高效增升装置技术等多种先进技术和新能源技术都被应用到民用航空运输当中。如今,增升装置设计需要多学科设计优化,这已在飞机设计中进行了大量的研究,国外R.C.Potter与L.P.Yip[2-3]等人提出一种反映气动性能、结构重量和成本的设计方法,国内唐家驹[4]等人借鉴了A350和波音787的后缘增升装置及其机构特点,搭建了大型飞机增升装置气动机构一体化优化设计平台。戴佳骅[5]等人以简单铰链为驱动机构,开展了起降构型的同步优化和机构设计工作。陈亚璨[6]等人针对驱动机构为连杆滑轨的翼型,进行了“后缘襟翼+扰流板同时下偏”的优化设计工作。
柔性机翼可以改变机翼展向和弦向的弯度,进而改变机翼表面的气体流动,提高气动效率,减少燃油消耗以及温室气体排放,可以调整展向载荷分布以减小翼根弯矩,还可以有效抑制激波,扩大抖振边界,能获得较刚性机翼更好的性能。正因为柔性变弯机翼这些优势的存在,可变弯度机翼成为未来大型飞机的研究热点。波音公司1980年的研究结果表明变弯度构型显著提高了整个飞行剖面非设计点的气动性能[7]。随着材料的不断发展,近年来,可连续变弯度的智能材料机翼成为了研究的热点[8],但是想要在工程上实现还有一定的困难。J.A.Hetrick[9]等人研究了任务自适应柔性机翼,飞行试验的结果表明在大部分范围内,升阻比可提高15%或者是更多。美国空军实验室的J.J.Joo[10-11]等人研究了“可变弯度机翼”,对比了机翼整体变弯和后缘部分机构变弯,结果表明在小迎角时整体变弯的机翼阻力更小,升阻比更大。T.Yokozeki[12-13]等人使用波浪结构来使襟翼变弯,该结构的驱动力较低,在小迎角时有较好的气动性能。沈广琛[14]等人研究了一套可用于现在和未来的民用客机机翼后缘变弯增升装置系统,提高了升力系数和升阻比。陆维爽[15]等人针对GAW-1翼型,进行了前后缘变弯度的气动性能的研究,明显改善了翼型的爬升性能。田云、全建冲[16]等人以NASA TrapWing模型为基础,提出了一种“柔性前缘下垂+单缝铰链襟翼+扰流板下偏+柔性尾缘襟翼”的智能增升系统,并进行多学科优化,得到气动、机构、结构综合最优的起降构型。王瑞[17]等人以DLRF11机翼为研究对象,设计一套基于反平行四边形机构的后缘襟翼柔性变弯机构,进行二维起降构型的气动/机构一体化优化设计,优化结果提高了起降构型的气动性能,巡航时的气动性能也有所改善。
本文以某大型宽体客机内段襟翼为基础,在襟翼内部安装一套柔性变弯机构,之后在该柔性变弯机构的带动下使襟翼实现柔性变弯,并且在后缘铰链襟翼机构的带动下使襟翼发生偏转,来进行起飞和着陆构型的三维机构运动导引下的二维气动/机构一体化的优化,优化目标以满足气动性能为主。
1 后缘襟翼柔性变弯机构介绍
以某大型客机内段机翼为研究对象,在襟翼后缘后50%部分的内部安装一套柔性变弯机构,要求该机构简单、重量轻。在该机构的带动下,襟翼后50%部分可以实现柔性变弯,襟翼前50%部分为刚性的,图1所示为巡航时的襟翼,CFlap为襟翼弦长,图中展示了巡航构型的柔性变弯位置,也就是后50%CFlap。

图1 襟翼巡航构型柔性变弯位置示意图
柔性变弯机构的机构简图如图2所示,图中只展示了襟翼的后50%部分,该机构由两级旋转机构组成,三角形A1A2A3为第一级旋转机构,三角形A3B1B2为第二级旋转机构,这两个三角形在A3处用铰链进行连接,A2为固定铰支,固定在襟翼的后梁上,用连杆将柔性变弯机构与襟翼蒙皮上的桁条进行连接。当OE1杆向前推动后,两级旋转机构就会向下偏转,襟翼也就会在连杆的带动下实现柔性变弯。变弯后的翼型与原始未变弯的翼型对比如图3所示,在原始刚性襟翼的基础上,柔性变弯后的襟翼可使襟翼后缘增加8°的偏角。

图2 柔性变弯机构的机构简图

图3 柔性变弯后的翼型与原始未变弯的翼型对比
新一代先进增升装置以A350XWB和波音787的增升装置为主,在其后缘增升装置中采用主动控制技术,使扰流板联合单缝襟翼同时下偏。单缝襟翼的机构采用简单铰链,简单铰链襟翼虽然没有富勒襟翼实现的富勒运动大,但是铰链襟翼可以使襟翼机构的复杂度降低,而且重量轻。为了减小襟翼打开时扰流板后缘和襟翼之间的间隙,需要在襟翼打开时使扰流板下偏,这样可以提高气动性能[18]。本文针对的某大型宽体客机内段机翼的前缘增升装置采用前缘下垂,后缘为简单铰链襟翼联合扰流板下偏。
内段襟翼所采用的机构如图4所示,机构点上标i表示内侧机构,机构点上标o表示外侧机构,R表示转动副,S表示球面副。内段襟翼为定轴转动,轴线为Ei和Eo两点所连的直线。

图4 内段襟翼机构
2 二维柔性增升装置气动机构一体化优化设计
2.1 计算方法与数值验证
因为没有带前缘下垂的二段翼的风洞实验数据,所以选用二维三段翼30P30N来进行数值验证。30P30N是公布于上世纪美国NASA的计算多段翼绕流的标准二维翼型,在多段翼型的CFD计算验证中使用的非常广泛。30P30N模型的参考弦长Cref=1 m,计算工况为马赫数Ma=0.2,雷诺数Re=9×106,网格量为13万,远场边界前缘和上、下部分为40倍参考弦长,后缘为80倍参考弦长,第一层网格高度为10-5倍弦长,网格如图5所示。计算求解器采用ANSYS CFX,湍流模型为SST。
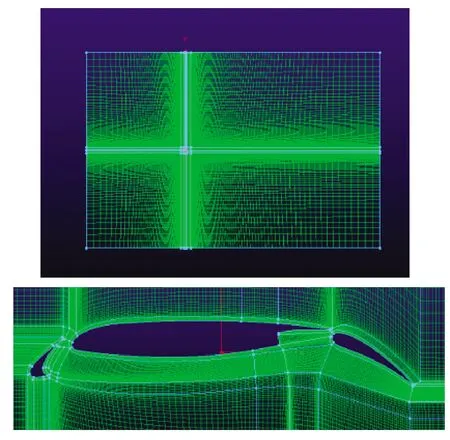
图5 30P30N网格
计算结果对比美国Douglas飞机公司[19]和NASA Langley研究中心的风洞实验结果[20],图6中所示的为襟翼、缝翼、主翼的升力系数以及总升力系数随迎角的变化曲线的计算结果与实验数据对比,从图中可以看出,总体上看升力系数数值计算值与实验值基本吻合,缝翼在高迎角时的数值计算值略大于实验值,在23°时发生失速,比实验值晚了2°失速。

图6 30P30N升力系数的数值计算与实验数据对比
图7为8°迎角下,30P30N的压力系数的数值计算结果与实验值的对比,从总体上看数值计算值与实验值吻合较好,缝翼上翼面的数值计算值略小于实验值,襟翼上翼面的数值计算值略大于实验值,襟翼尾缘部分略有偏差。

图7 8°迎角下30P30N压力系数的计算值与实验值对比
总体来看,数值计算的结果与实验值吻合较好,所以认为数值计算的结果是可行的。
2.2 气动机构一体化优化设计
本文以某宽体客机的内段外侧顺气流机构布置剖面为原始构型,干净构型的弦长c=8 270.415 mm,采用“前缘下垂+扰流板下偏+后缘铰链襟翼+襟翼后缘柔性变弯”的增升装置设计方案,在内段襟翼机构的三维运动的带动下,同时后缘襟翼柔性变弯机构带动襟翼后缘进行柔性变弯,在襟翼和扰流板绕各自轴运动到不同位置后截取同一顺气流位置的剖面,对起飞构型和着陆构型分别进行二维增升装置气动机构一体化优化设计,优化在ISIGHT软件中进行。均采用正置翼进行计算,并将计算结果转换到斜置翼上。
起飞时的优化变量共有7个见表1,分别为:扰流板下偏角度、襟翼下偏角度、柔性变弯机构驱动杆OE1移动距离、襟翼转轴点Ei的x坐标、襟翼转轴点Ei的y坐标、襟翼转轴点Eo的x坐标、襟翼转轴点Eo的y坐标,柔性变弯机构驱动杆移动距离也就决定了襟翼柔性部分的下偏量,各优化变量的取值范围如表1所示。大型民用飞机在起飞时,需要较大的升力系数以及升阻比以增加飞机爬升梯度、减小发动机推力,因此优化目标有2个,分别为8°迎角下升力系数最大、8°迎角下升阻比最大。优化算法选取非支配排序遗传算法(Non-Dominated Sorting Genetic Algorithm-II,简称NSGA-II)。设置计算20代,每代24个子代,共计480个计算工况。

表1 起飞优化变量
着陆时的轴线就采用起飞时优化出来的轴线,着陆时的优化变量有3个,分别为:扰流板下偏角度、襟翼下偏角度、柔性变弯机构驱动杆移动距离,各优化变量的取值范围如表2所示。优化目标与起飞不同,着陆时飞机的升力系数是唯一需要考虑的因素,而升阻比则不需要考虑,因此优化目标只有一个,为8°迎角下升力系数最大,为单目标优化,因此采用多岛遗传算法(Multi-island Genetic Algorithm),共计500个计算工况。

表2 着陆优化变量
后缘襟翼柔性增升装置气动机构一体化优化流程如图8所示。首先进行襟翼后缘柔性变弯的有限元计算,需要在MATLAB中生成在改变后缘柔性增升装置中驱动杆推动的距离后得到的可以在ANSYS APDL中进行自动计算的APDL程序;然后在ANSYS APDL中通过运行MATLAB中生成的APDL程序,可以自动进行有限元计算,得到柔性变弯后的翼型;之后在MATLAB软件中进行翼型参数化,使得在改变优化变量的值后可以自动得到新的起飞或着陆翼型;接着用POINTWISE软件进行网格自动划分;然后使用CFX软件进行自动气动计算;最后进行优化,得到气动性能最优构型。
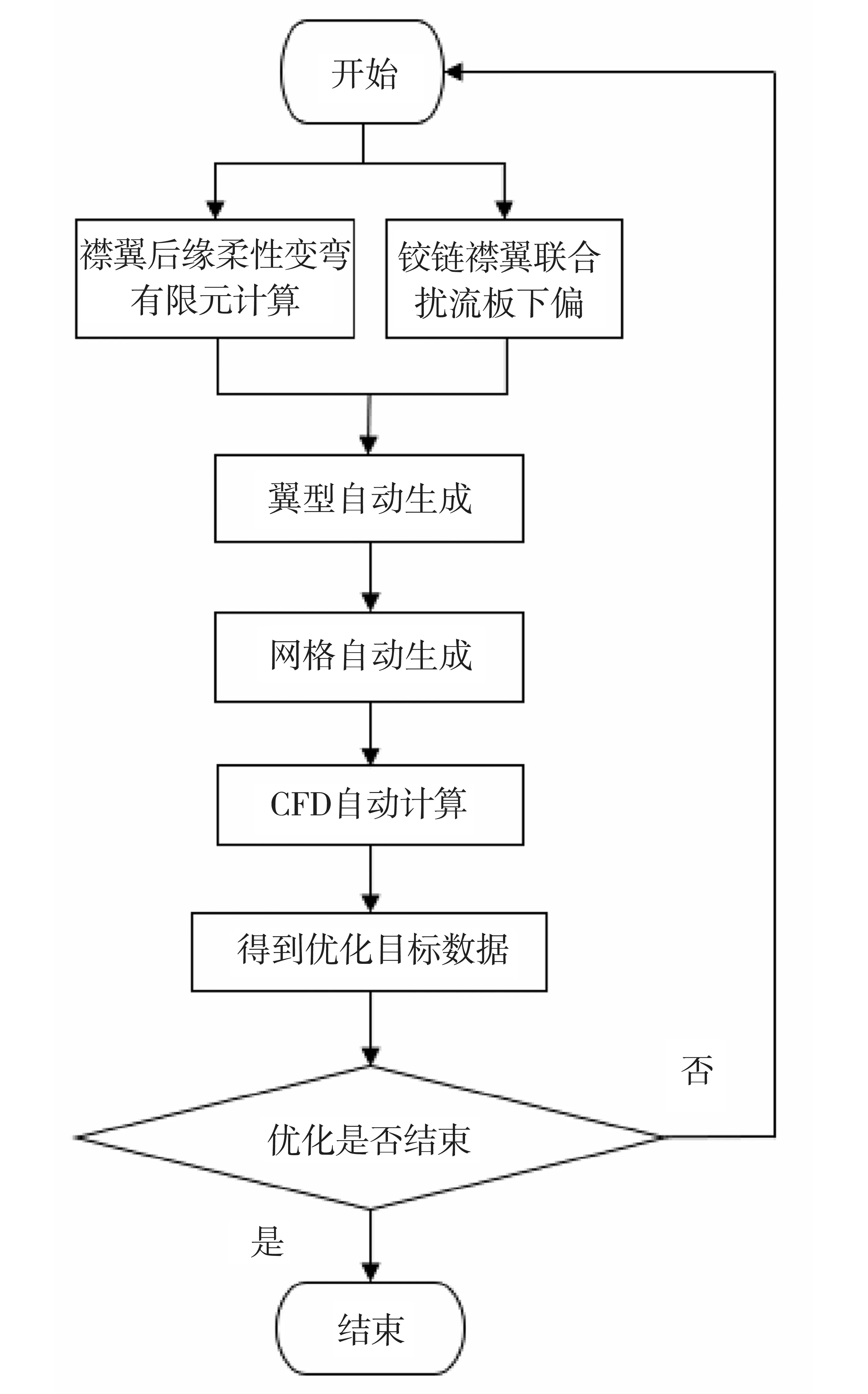
图8 后缘襟翼柔性增升装置气动机构一体化优化流程图
3 二维柔性增升装置气动机构一体化优化设计结果
3.1 起飞构型优化结果
起飞构型在ISIGHT中进行480轮优化,得到的优化结果如图9所示,横坐标为升力系数,纵坐标为升阻比,Pareto前沿在图中也可看出,从Pareto前沿上选取A、B、C三个点进行分析。
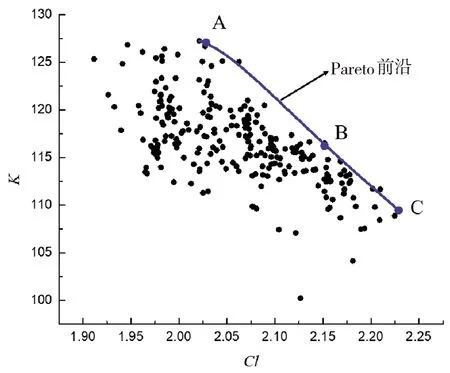
图9 起飞构型优化结果
A、B、C三点的翼型与原始翼型的对比如图10所示,从图中可以看出,三组翼型襟翼尾缘的下偏量依次增大。这三组构型的优化变量的值以及原始构型的优化变量的值如表3所示,三组构型以及原始构型的缝道参数gap和overlap如表4所示。

图10 三组构型翼型对比

表3 三组构型的优化变量以及原始构型的优化变量

表4 三组构型以及原始构型的缝道参数
这三组构型的气动性能与原始构型的对比如图11所示。从图(a)中可以看出,A、B、C三组构型与原始构型相比,升力系数都有所增加,A构型增加的最少,C构型增加的最多。A构型在13°时失速,B构型在12°时失速,C构型在12°时失速。从图(b)中可以看出,A、B、C三组构型与原始构型相比,阻力系数也都有所增加,A构型增加的最少,C构型增加的最多。从图(c)中可以看出,A、B、C三组构型与原始构型相比力矩系数都有所减小,A构型减少的最少,C构型减少的最多。从图(d)中可以看出,当升力系数较小时,只有A构型的升阻比是大于原始构型的,升力系数较大时,三组优化构型的升阻比都大于原始构型。

(a)升力系数对比
综合而言,A构型的升力系数有所增加,在升力系数较小和升力系数较大时A构型的升阻比都有所增加,因此选取A构型为最优构型。A构型的最大升力系数与原始构型相比的增加量为0.119。图12所示为8°迎角下最优构型的压力系数与原始构型的压力系数的对比,从图中可以看出,最优构型和原始构型下翼面的压力系数相差不大,前缘以及襟翼的吸力峰增加。

图12 8°迎角下起飞最优构型的压力系数与原始构型对比
图13为起飞最优构型的压力云图及流线图,从图中可以看出,在8°迎角下,起飞最优构型未发生分离,在13°迎角下襟翼上表面即将发生分离,14°迎角下襟翼上表面有分离涡的出现,发生分离,15°迎角下襟翼上表面有更大面积的分离涡产生,发生大面积分离。
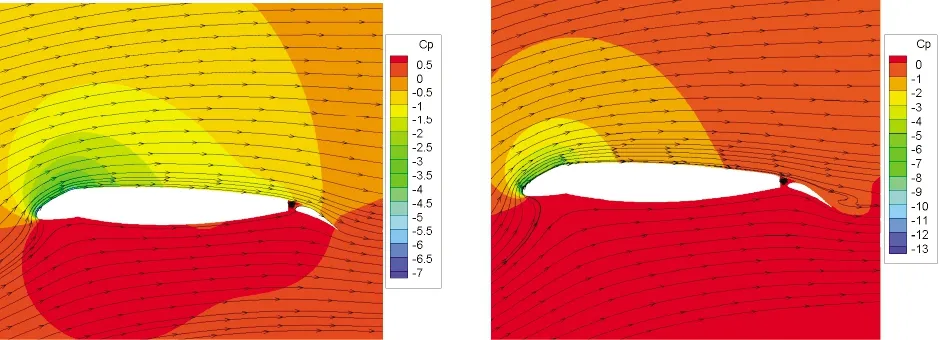
(a)8°迎角 (b)13°迎角
3.2 着陆构型优化结果
着陆构型在ISIGHT软件中共进行500轮优化,得到的最优构型和原始构型的翼型对比如图14所示,最优构型襟翼尾缘的下偏量与原始构型相比有所增大。着陆最优构型以及原始构型的优化变量的值如表5所示,缝道参数gap和overlap的值如表6所示。

图14 着陆最优构型与原始构型的翼型对比

表5 着陆最优构型以及原始构型的优化变量值

表6 着陆最优构型以及原始构型的缝道参数的值
着陆最优构型与原始构型气动性能的对比如图15所示,从图(a)中可以看出,着陆最优构型在11°时失速,比原始构型晚1°失速,最大升力系数为2.604。线性段最优构型和原始构型的升力系数相差不是很大,最优构型的升力系数略微大于原始构型,在失速段最优构型的升力系数明显大于原始构型。从图(b)中可以看出,除11°迎角以外,其余迎角下的最优构型的阻力系数均大于原始构型的阻力系数。从图(c)中可以看出,线性段的力矩系数最优构型和原始构型相差不大,失速段最优构型的力矩系数小于原始构型。最优构型的最大升力系数比原始构型的最大升力系数提高0.162。
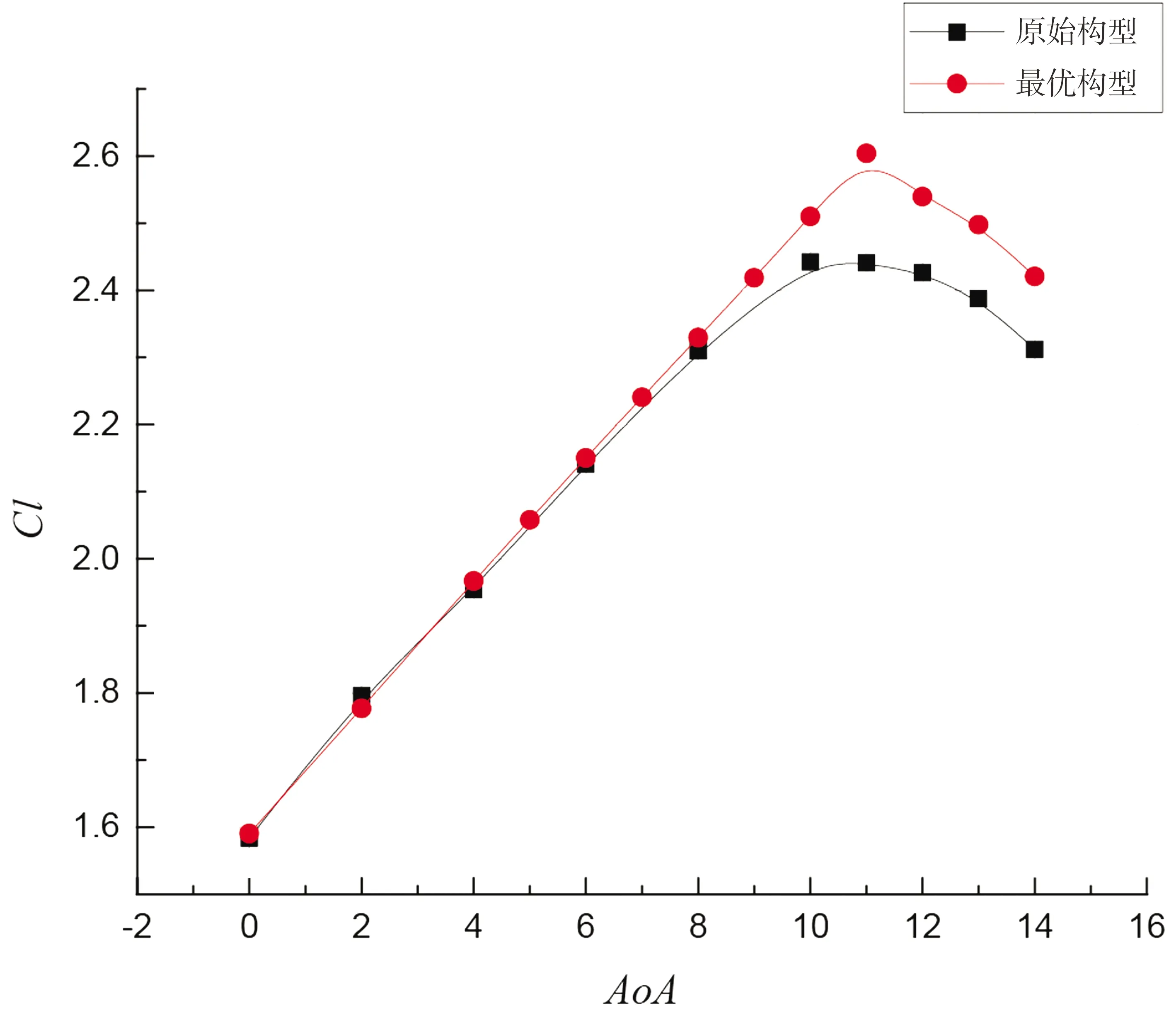
(a)升力系数
图16为着陆最优构型与原始构型8°迎角下的压力系数的对比图,从图中可以看出,最优构型后缘襟翼前缘的压差较原始构型相比有所增大。

图16 8°迎角下着陆最优构型的压力系数与原始构型对比
图17为着陆最优构型的压力云图及流线图。从图中可以看出在11°迎角时即将失速,此时襟翼后部还是存在分离区,12°迎角时紧贴襟翼的分离区消失,流动存在附着流,存在分离涡,此时已经失速。14°迎角时襟翼尾缘存在更大面积的分离涡。

(a)8°迎角 (b)11°迎角
4 结论
1)本文基于某大型宽体客机内段襟翼,在后缘铰链襟翼机构的带动下,并且襟翼后缘在柔性变弯机构的带动下实现柔性变弯,进行了起飞和着陆构型的气动/机构一体化优化设计。起飞优化出的最优构型与原始构型相比,最大升力系数的增加量为0.119,并且在相同的升力系数下,升阻比有所增大。
2)着陆优化出的最优构型与原始构型相比,最大升力系数的增加量为0.162,且最优构型推迟1°迎角失速。
3)优化所得的起飞和着陆构型均提高了原始构型的气动性能。

