Libration and end body swing stabilization of a parallel partial space elevator system
Gefei SHI, Gngqing LI, Zheng H. ZHU,*
a School of Aeronautics and Astronautics, Sun Yat-Sen University, Guangzhou 510275, China
b Department of Mechanical Engineering, York University, Toronto, Ontario M3J 1P3, Canada
KEYWORDS Libration stabilization;Nonlinear dynamics;Optimal control;Parallel partial space elevator;Space tether
Abstract This paper studies the libration and stabilization of a parallel partial space elevator system in circular orbits.The system is made up of two paralleled partial space elevators,each of which consists of one main satellite, one end body and a climber moving along the tether between them.The libration characteristics of the elevator are studied through numerical analysis by a new dynamic model, and a novel control strategy is proposed to stabilize the swing of the end body by projecting the climber speeds only.Optimal control method is used to implement the new control strategy in the case where the climbers move in opposite direction. The simulation results validate the effectiveness of the proposed control strategy whose application will neither sacrifice the transport efficiency nor exacerbate libration significantly.
1. Introduction
Partial Space Elevator (PSE) is a promising and expansible technology in long-range cargo transfer in space in the near term.1-4It generally consists of one main satellite and one end body connected by a tether with one or multiple climber(s) moving along the tether.5As an extended application of the classical PSE system, the Parallel Partial Space Elevator(PPSE) system takes advantage of the PSE with higher efficiency of payload transfer ability by more alternative transfer patterns. A PPSE system generally consists of two paralleled PSEs connected by rigid rods at the bottom and top ends.
Although limited studies have been devoted to the PPSE system, the investigation of PSE can be used as a reference for the study of dynamics and stabilization of the PPSE system. In the area of dynamics, Refs. 6,7 studied the dynamics of PSE using a Two-Piece Dumbbell Model (TPDM) that was latter validated by Ref. 8 through ground-based experiments.Based upon the TPDM,the effects of the climber speed and the mass ratio of the climber over the end body on the dynamics of PSE were studied in Refs. 9,10. Furthermore,Ref. 11 investigated the effect of tether flexibility on the dynamics of PSE by a three-dimensional high-fidelity model based on the Nodal Position Finite Element Method(NPFEM). Compared with the TPDM, the NPFEM captures the flexible modes of the tether and validates the motions of the climber and the end body predicted by the TPDM.11,12However, the TPDM is much more computationally effective than the NPFEM.The studies in Refs.11,12 indicates that the TPDM is accurate enough to describe the relative motion of tethered space systems while being computationally efficient,which is in favor of dynamic control. In addition, Ref. 5 proposed a multi-climber PSE system that consists of several climbers arranged from the main satellite to the end body connected by tethers. Then, a generalized model for a multiclimber PSE was proposed in Ref.13 and the effect of different moving patterns on tether libration was studied in Ref.14.Up to date,the dynamic analysis of PPSE is limited due to its distinctive structure.
The stabilization of a PPSE system is critical to practical applications. Previous investigations14-20reveal some effective methods that could be potentially used for stabilizing the libration of the climbers and the end bodies of a PPSE system.For instance,it is possible to suppress the libration by adjusting the climber speed,21which can be implemented by tension control.Furthermore, thrust control is also used to stabilize the libration of PSE (or a three-body tethered system).22,23Under the actuation of thrusters, a PSE system can be controlled effectively with better performance than by tension control only.However, this might be challenging in real applications10and may reduce the potential payload capacity of the climber.Apart from the libration suppression, the stabilization of the end body system of PPSE is also a concern.Since the end body system, which consists of two end bodies connected by a rod,will swing in the transfer phase due to the tether swapping of PPSE.Thus,it is critical to suppress the swing of the end body system to ensure a successful payload transfer.
The current work aims to explore the dynamic characteristics of a PPSE and suppress the swing of the end body system.First, a new dynamic model is derived based upon a parallel two-piece dumbbell model to describe the motion of the novel PPSE accurately and efficiently.Second,the effects of the climber speed and the mass ratio of the climber over the end body on the libration dynamics of the PPSE is analyzed. New dynamic characteristics in tethered space systems caused by the swing of the end body system is studied in the first time.Finally,a novel non-thrust control strategy is proposed to suppress the swing of the end body system by optimal control scheme due to its wide application.24-27The proposed control strategy is validated by numerical simulation.The results show that by projecting the climber speeds along tethers, the swing angle of the end body system can be suppressed between the desired boundaries in an efficient transfer manner with thrust free at the climbers and the end bodies.
2. Mathematical formulation
This work aims to explore the dynamics and control of the relative libration motion of a PPSE. For simplicity, a PPSE system is modeled by the TPDM approach in the work.The PPSE consists of two PSEs (PSE I and PSE II) connected by inelastic, massless, and straight rod structures at the main satellites and end bodies, see Fig. 1. The assumption of massless tether is based on the authors’ previous studies in the dynamic modeling of a PPSE, where the tether was treated as a 3-dimensional elastic flexible tether by the nodal position finite element method.11,12The study showed the tether mass has very limited effects on the global libration tendencies of the climbers and the end body,except some local flexural deformation of tethers.Moreover,the comparison study in Refs.11,12 also shows the difference in the results of the finite element model and the simple dumbbell model is negligible. Thus, to make the dynamic model simple and clear in studying the global dynamic characteristics of large scale PPSE systems, it is reasonable to ignore the mass of the tether.Furthermore,compared to the length scale of the PPSE, the rotation motion of the main satellite and the end body is local and has negligible effect on the overall relative libration motion of the PPSE.Thus, the attitude motions of the main satellite and the end bodies are ignored. The PPSE system is subject to a central gravitational field. All other external perturbations, such as atmospheric drag force and solar radiation pressure, are neglected. Moreover, climbers are simplified as two lumped masses (m1, m3) due to the negligible ratio of the climbers’dimensions over the tether length. The libration motion is described in an inertial frame OXY with the origin at the Earth’s center, which is aligned with the orbital plane. This is because,the motion of the PPSE is mainly in the orbit plane,the out-plane motion has very weak effect on the in-plane motion due to the high order coupling.Therefore,the dynamic model is derived in the two-dimensional orbit plane.The position of the main satellites’ centroid (M) can be denoted by a vector r measuring from O. In PSE I, the main satellite MI,climber m1and the end body’s mass point m2are connected by tethers with the lengths of L1and L1s, respectively. The libration angles of the m1and m2(θ11and θ12) are measured from the unit vector erof r. Similarly, the parameters of PSE II (L2, L2s, θ11and θ12) are defined in a similar way as shown in Fig. 1. The centroid (M) of the main satellite system is assumed moving in a circular Kepler orbit, and the relative positions of MIand MIIrespect to M are fixed, see Fig. 1.Based upon these assumptions, the positions of the PPSE system can be written as,
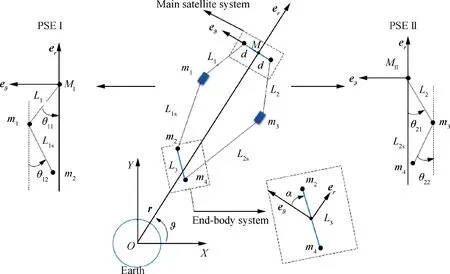
Fig. 1 Parallel partial space elevator system.

where μ is the gravitational constant of the Earth.
Then,the dynamic equations of the PPSE can be derived by Lagrange equation,

The internal force of rod L3is expressed by T3with positive value for tension and negative value for compression, respectively. The detailed dynamic equations are shown in the Appendix A.
3. Libration of parallel partial space elevator
The PPSE is assumed orbiting in a circular orbit with r=42164 km. System parameters are listed in Table 1. The total tether lengths of PPSE I and II are both constant and expressed as L0.The dynamic simulations in this work are carried by MATLAB with RK-4 integrator. The time step in is 0.001 s.
3.1. Effects of climber speed and moving patterns
The effects of climber speed on the libration of the PPSE system are studied by assuming the climbers moving along the tethers at a constant speed in three different patterns.The total length of tethers is constant, such that
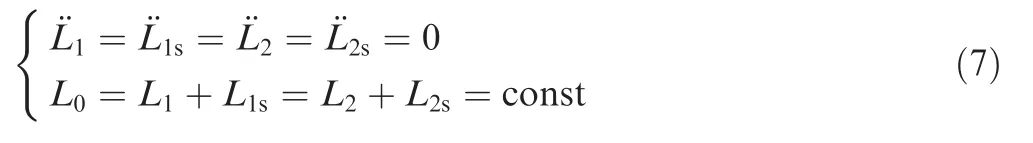
Substituting Eq. (7) into Eq. (5) with the consideration of Eq. (6) yields the expression of uncoupled tensions , T1s, and T2sin tethers , L1s, and L2sin terms of , respectively.
Thus, the libration dynamic equations have the form of


Table 1 System parameters.

3.1.1. Pattern 1: Two climbers move upwards from the end bodies towards the main satellites

When the climber speed ˙L1grows,the magnitude of Eq.(9)increases,which enlarges the libration amplitude of θ11.In the case when the speed is 200 m/s,the libration angle of the climber grows monotonously and reaches 0.79 rad by the end of the simulation, see Fig. 2(a) and (b). This is because the L1decreases quickly as the climber moves, and the effect of the Coriolis force is much greater than the libration suppression effect produced by the gravity and the tether tension. Similar results are also observed in Ref. 14. Fig. 2(c) shows the end body system’s swing angle α. It should be noted that the α is not a general coordinate, whose definition is shown in Fig. 1,and it can be derived by
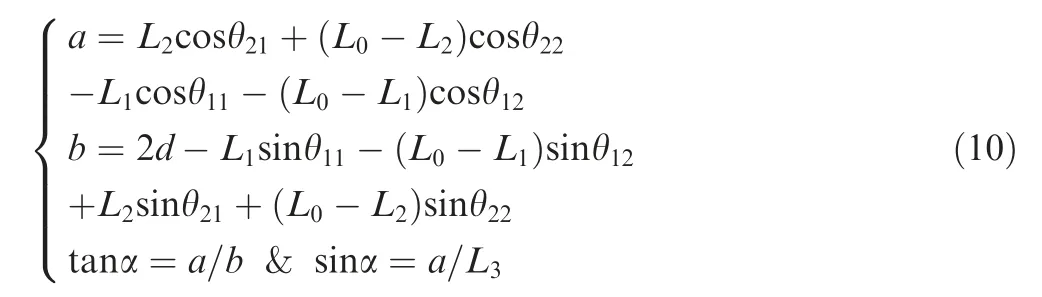
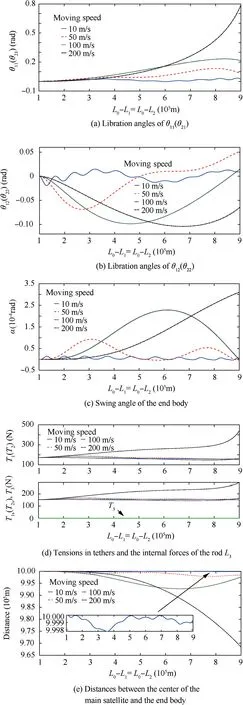
Fig. 2 Libration of the PPSE under different moving speed in upward transfer.
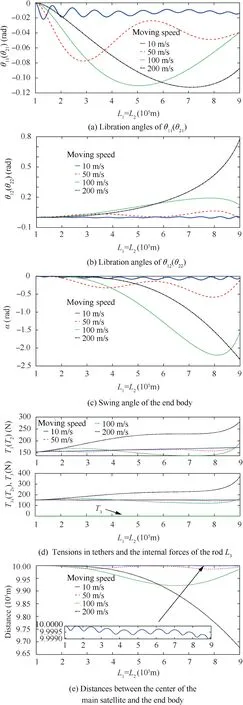
Fig. 3 Libration of the PPSE under different moving speeds in the downward transfer.
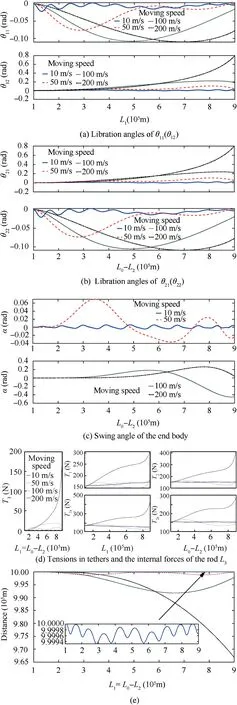
Fig. 4 Libration of the PPSE under different moving speeds in climber 1 (m1) downward & climber 2 (m3) upward transfer.
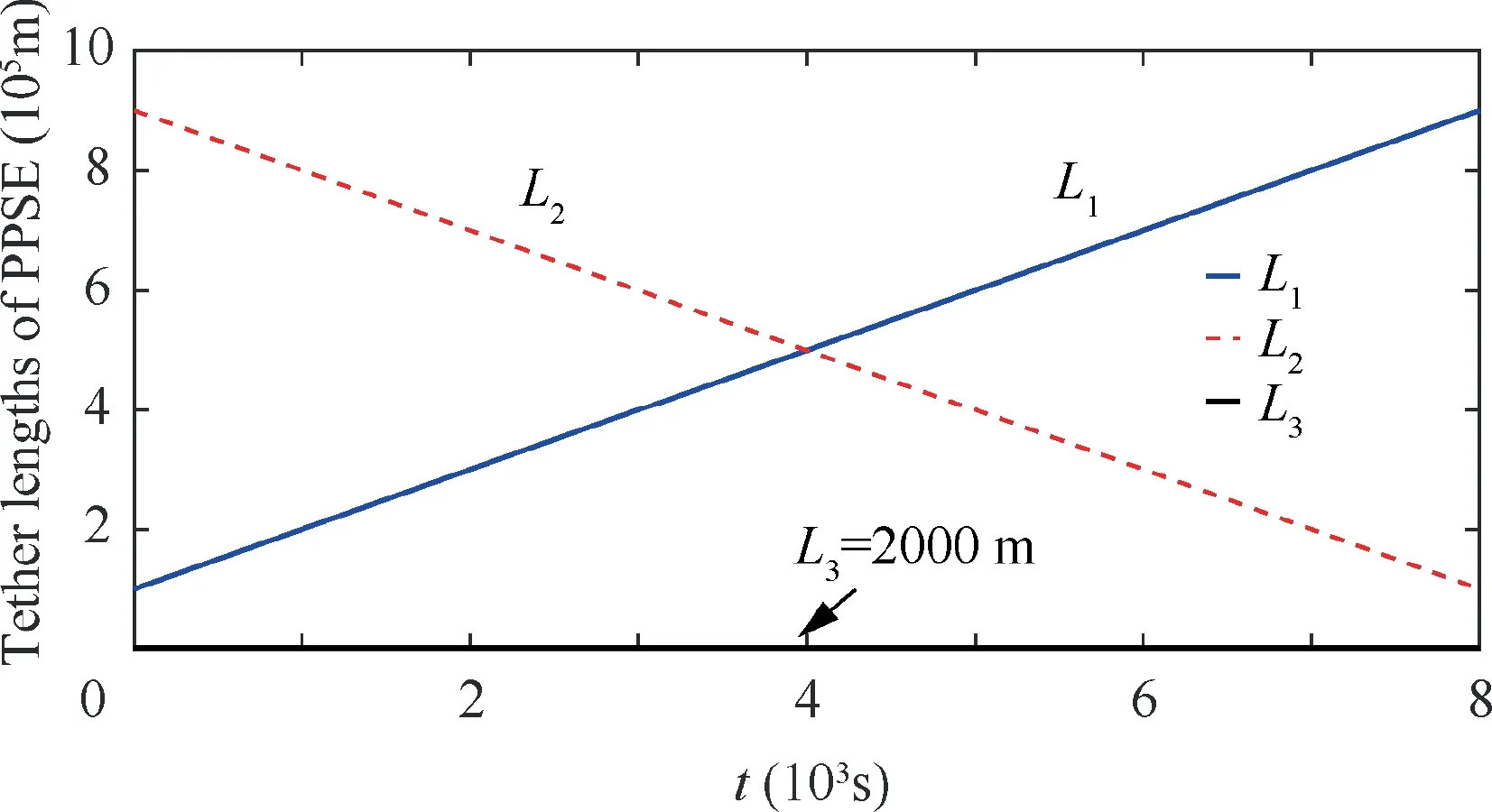
Fig. 5 Tether lengths of L1 & L2 and L3.
It should be noted that the quadrant should be considered when calculating α. It can be found that, although the amplitude of α increases with the growing of the climber speed, its order is not greater than 10-4rad, which is very small compared with the libration angles shown in Figs. 2(a) and (b).This is because, in this pattern, the α is mainly caused by the difference of gravity orientations between two end bodies which is very small. The tensions in tethers and internal force in the rod L3that links two end bodies are shown in Fig.2(d).The magnitudes of the tensions in tethers increase as the climbers’ moving speeds increase. When the climbers move upwards with the speed of 200 m/s,the tensions in both pieces of the tethers are obvious greater than those in slower speed cases. In this moving pattern, the internal force in the rod is nearly zero due to the nearly parallel motions of the PPSE I and II, see Fig. 2(d) T3. It should be noted that the internal force in the rod is not strictly zero although its magnitude can be ignored in this pattern. This is because, to make the PPSE I and II nearly parallel in structure strictly, the rod should be a curved one with a curvature equals to the orbit of the end bodies which also lead to the fluctuation of in this nearly paralleled moving pattern. Since the length of the rod is much less than the orbital radius, the internal force in the rod is ignorable. The results in Fig. 2 (d) also show that the tensions in each pieces of the tethers are greater than zero,this denotes that all tethers are kept tightening.Fig.2(e)shows the distances between the center of the main satellite and the end body in each case. The greater moving speed of the climber corresponds to larger distance magnitude, such phenomenon matches the libration of the climbers in this pattern, see Fig.2(a).This is because in this moving pattern,the libration of the climber leads the main distance changing,and the libration of the end body show slight differences in different speed cases.
3.1.2. Pattern 2: Two climbers move downwards from the main satellite to the end body


3.1.3. Pattern 3: One climber (m1) moves downwards and the other climber (m3) moves upwards
In the aforementioned patterns, climbers move in parallel in the same direction. In the current pattern, climbers move simultaneously from the main satellite (MI) and the end body(m4)at same speed and in the opposite directions along tethers with the initial values L1(0)=0.9L0, L2(0)=0.1L0, L1(tf)=0.1L0and L2(tf)=0.9L0. The tether lengths are shown in Fig. 5. The initial libration states are zero.
As can been seen in Fig.4(a)and(b),the magnitudes of the libration angles grow with the increase of the moving speed,due to the increase of the magnitudes of Coriolis forces.Significant difference is observed from the results in Fig.4(c).When the climbers move at the speed of 10 m/s, the angle fluctuates around zero with the magnitude less than 0.1 rad. Although such attitude change in the current pattern is much smaller than other cases with higher speeds compared with the results in Figs.2(c)and 3(c),the magnitude of is much greater.This is due to the tethers in the system are no longer parallel. In this pattern, the Coriolis forces acting on PSE I and PSE II are in opposite direction, such that, the line between two climbers neither parallel to the main satellite system (line MIMII) nor the end body system (line L3). This leads to the unparalleled shape in the transfer phase as shown in Fig.6.It can be found that, the magnitudes of grows with the speed increase significantly. In the case when the speed is 100 m/s, the maximum amplitude of approaches 0.45 rad, which is 3 orders higher than those in the Pattern 1 and 2. The results also indicates that the length of L3=2000 m keeps constant in each case,which validates the dynamic model in this work, see Fig. 5.The tensions in tethers and the rod L3are shown in Fig. 4(d). Although the variation trends of the tensions in tethers are similar to those in the previous patterns,the tension results show more variations in this unparalleled moving pattern due to the PPSE’s unparalleled shape in the transfer period. Such unparalleled shape also acts on the rod linked between two end bodies. Compared with the results in Figs. 2(d) and 3(d),the tension in the rod will not be kept zero in the unparalleled pattern, see Fig. 4 (d) T3. When the climbers move at a relatively slow speed of 10 m/s,the internal force in the rod L3varies around zero.This indicates the rod is switching between tension and compression. With the increment of the climbers’speed,the internal forces in the rod are tensile forces,see Fig.4(d).The distances between the main satellite and the end body show similar characteristics with those previous patterns,compare Figs.2(e),3(e)and 4(e).This indicates that the unparalleled shape leads limited distance change compared with the total libration of the system.
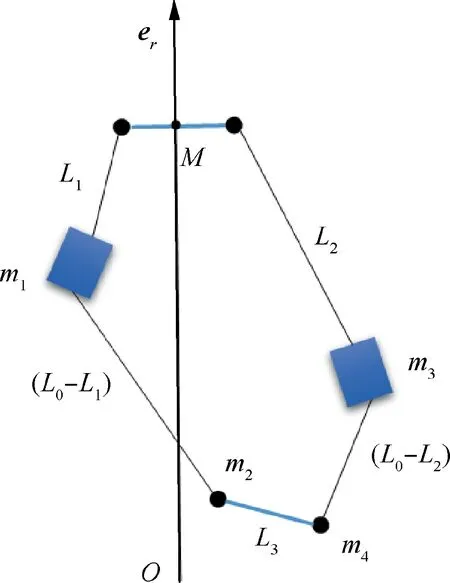
Fig. 6 Unparalleled shape of the PPSE.
In summary, the growth of the climbing speed exacerbates the libration which amplifies the tensions in tethers. Unparalleled moving pattern such as the Pattern 3 causes obvious attitude changes on the end body system. Moreover, the unparalleled shape of the system will lead obvious internal force in the rod. These phenomenon becomes worse with the increase of the climber speed.
3.2. Effects of mass ratios
The effects of mass ratios on the libration motion is studied in the upward and downward transfer cases. The system parameters are listed in Table 1. As shown in Fig. 7, the climbers move upwards at the speed of 50 m/s. When the mass ratio is small,for instance 0.1,the libration is small due to the libration moment produced by the Coriolis force acting on the climber is negligible compared with the restoring moment caused by gravity of the end body.As the mass ratio grows, the maximum amplitudes of both libration angles increase especially for the climber (θ11), comparing Fig. 7(a) and (b). The magnitude of the libration angle θ11approaches 1.3 rad at the mass ratio m1/m2=1,see Fig. 7(a). The effects of mass ratio in the downward case are shown in Fig. 8. As the mass ratio grows,the maximum magnitudes of libration angles increase,which is similar to that in the upward case.
In summary, the increase of mass ratio of the climber over the end body exacerbates the libration of the system,especially for the case when the climbers are moving upwards as shown in Figs.7 and 8.Thus,the small mass ratio of the climber over the end body should be considered in application.

Fig. 7 Effects of mass ratio in upward transfer.
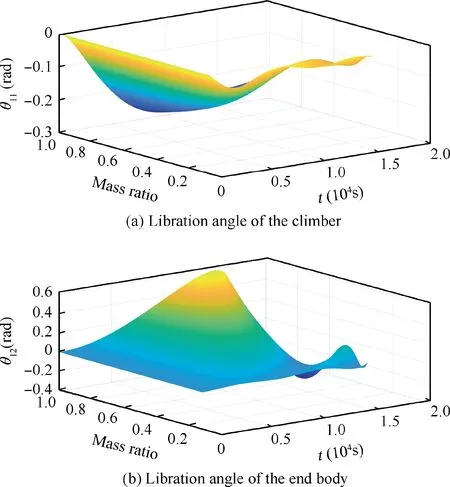
Fig. 8 Effects of mass ratio in downward transfer.
In summary,the increase of both the climbers’moving speed along tethers and the mass ratio of the climber over the end body exacerbates the libration of the PPSE system, especially for the upward cases. Different from the PSE system, the attitude of the end body system is a new parameter and should be considered to ensure the stability of the PPSE system.In parallel moving patterns such as the Pattern 1 and 2, the swing angle of the end body system changes slightly. However, as observed in the Pattern 3, when the moving directions of the climbers along tethers are opposite, the attitude (α) of the end body system changes significantly and must to be stabilized.
4. Attitude stabilization of the end body system with optimal control
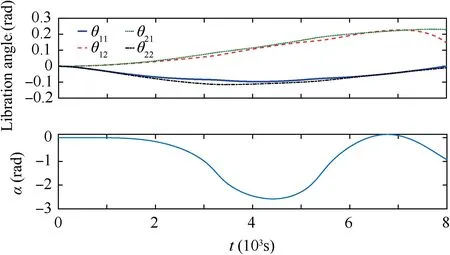
Fig. 9 Libration and swing without control.
As discussed above, when the climbers move in opposite direction along tethers, the swing of the end body system is significant which will exacerbate the system stability.Therefore,it is necessary to consider the attitude stabilization of the end body system. Consider the mass of two climbers are m1=1000 kg and m3=2000 kg,respectively.The other system parameters are given in Table 1.The initial libration is assumed zero.The climbers move in the pattern 3 at the speed of 100 m/s along tethers with constant total lengths, such that, L1(0)=0.1L0, L2(0)=0.9L0, L1(tf)=0.9L0and L2(tf)=0.1L0.The tether states are given in Eq.(7).First,the transfer of climbers without controlled over 8000 s is analyzed and the results are shown in Fig. 9. It shows clearly that the magnitude of for the end body approaches 2.7 rad in the simulation although the libration angles of tethers change smoothly with the maximum magnitude less than 0.25 rad.This indicates(A)the endbody system tumbles in this transfer phase,which will lead to instability of the PPSE system;and(B)different climber masses exacerbate the attitude of the end body system,see Figs.9 and 4.Thus,it is necessary to stabilize the swing of the end body system.
Based upon Eq.(10),the stabilization α of is coupling with libration angles and tether lengths.Differentiating the left and right sides of Eq. (10) can obtain,

4.1.Case 1:the attitude stabilization of the end body system with minimal control inputs
The aim of optimization is to minimize the control input,such that,

where vrelpresents the magnitude of the relative motion speed between the center of the end body and the main satellite. It should be noted that in Eq. (13) the fixed relative speed between the center of the end body and the main satellite,which is led by the orbital radius difference, has been diminished. Thus, vrelcan also be regarded as the relative motion speed between the end body and its initial state which presents the additional relative motion speed between the main satellite and the end body lead by the system libration.
The results are shown in Figs. 10-14. Fig. 11 shows the swing of the end body system in the transfer phase under the actuation of speed projecting.Compared with the uncontrolled case,the attitude of the end body is stabilized.In the period of 0-2000 s,the angle α decreases from zero to-0.37 rad continuously.Then,with the speed adjusting,the angle α is stabilized near the bottom.By the end of the transfer phase,the final α is-0.4 rad.The influence of control on the libration motions are shown in Fig. 10. Compared with the uncontrolled case, the libration motions of PSE I (θ11and θ12) are suppressed globally by the speed projecting. The maximum magnitude of θ12is 0.13 rad,which is less than 0.22 rad in the uncontrolled case,see Fig.9.The libration angle θ11changes slightly in two cases.On the contrary,the libration motions of PPSE II(θ11and θ12)are amplified as a cost of the end body’s stabilization. In the period of 0-6500 s, the libration angle of θ21is similar to that in the uncontrolled case, see Fig. 9. After that, the libration angle of θ21increases continuously and approaches to 0.32 rad by the end in Case 1, which is greater than that in Fig. 9. The libration angle of θ22is amplified slightly under the control,and approaches to 0.05 rad by the end of the transfer phase, which is greater than zero in the uncontrolled case,see Figs. 9 and 10. Furthermore, by comparing results in Figs. 11 and 5, it can be found that the tether lengths under the actuation of the control inputs in Fig. 12 fluctuate slightly around the results of non-controlled case. The tensions in the tethers and the internal force in the rod are shown in Fig. 13.The tensions and the internal force show obvious fluctuations in the simulation due to the changes of the climbers’ accelerations,see Fig.12.However,all tether tensions are greater than zero due to the control constraint. The results in Fig. 13 indicate that the adjusting the climber speeds will lead obvious variation of tensions and internal force of the rod, which should be considered in the control design to avoid tether slacking. The distance and the magnitude of the relative motion speed between the end body and the main satellite are shown in Fig. 14. Under the optimal control, the magnitude of the relative motion speed is limited within its bounds.
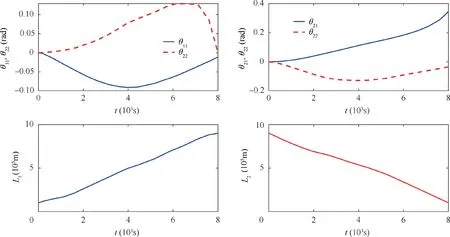
Fig. 10 Libration angles and tether lengths.
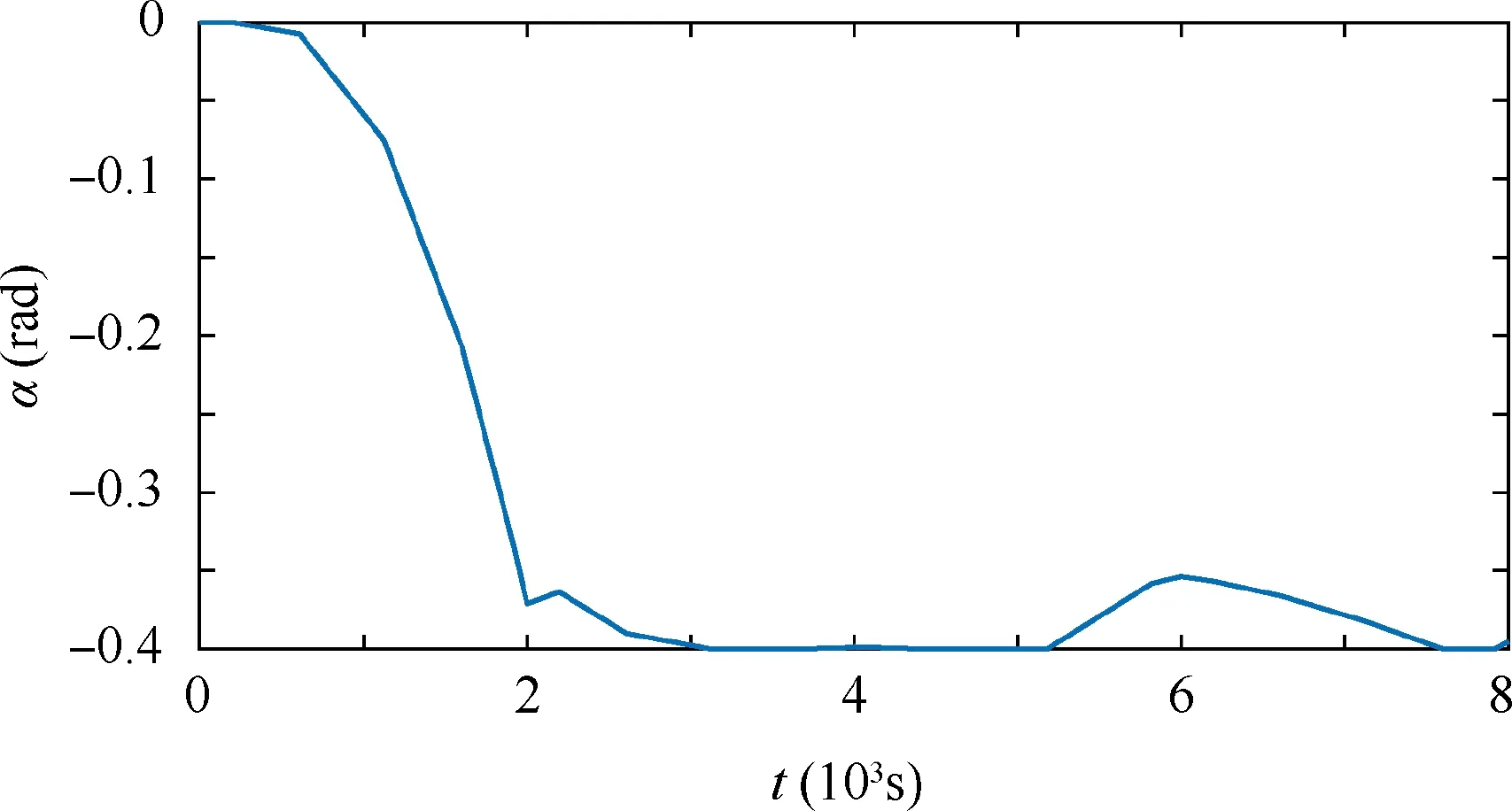
Fig. 11 Swing angle of the end body.
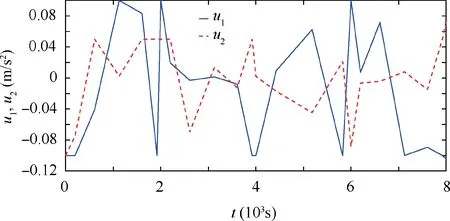
Fig. 12 Control inputs.
4.2. Case 2: Stabilization of the end body system by minimizing total swing of α over the transfer phase.
The aim of the optimization is to minimize the total swing of the end body over the transfer phase, such that,
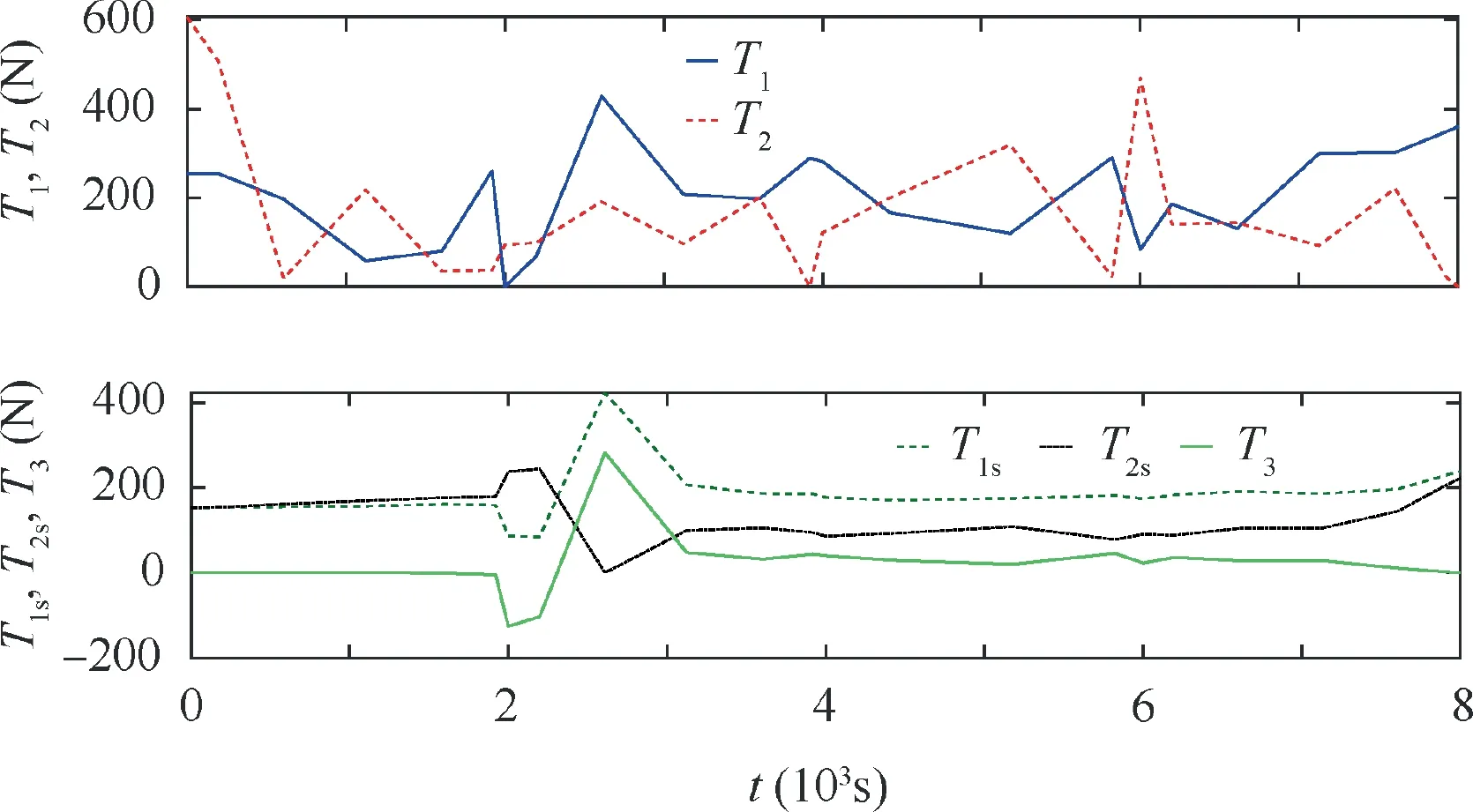
Fig.13 Tensions in tethers and the internal forces of the rod L3.
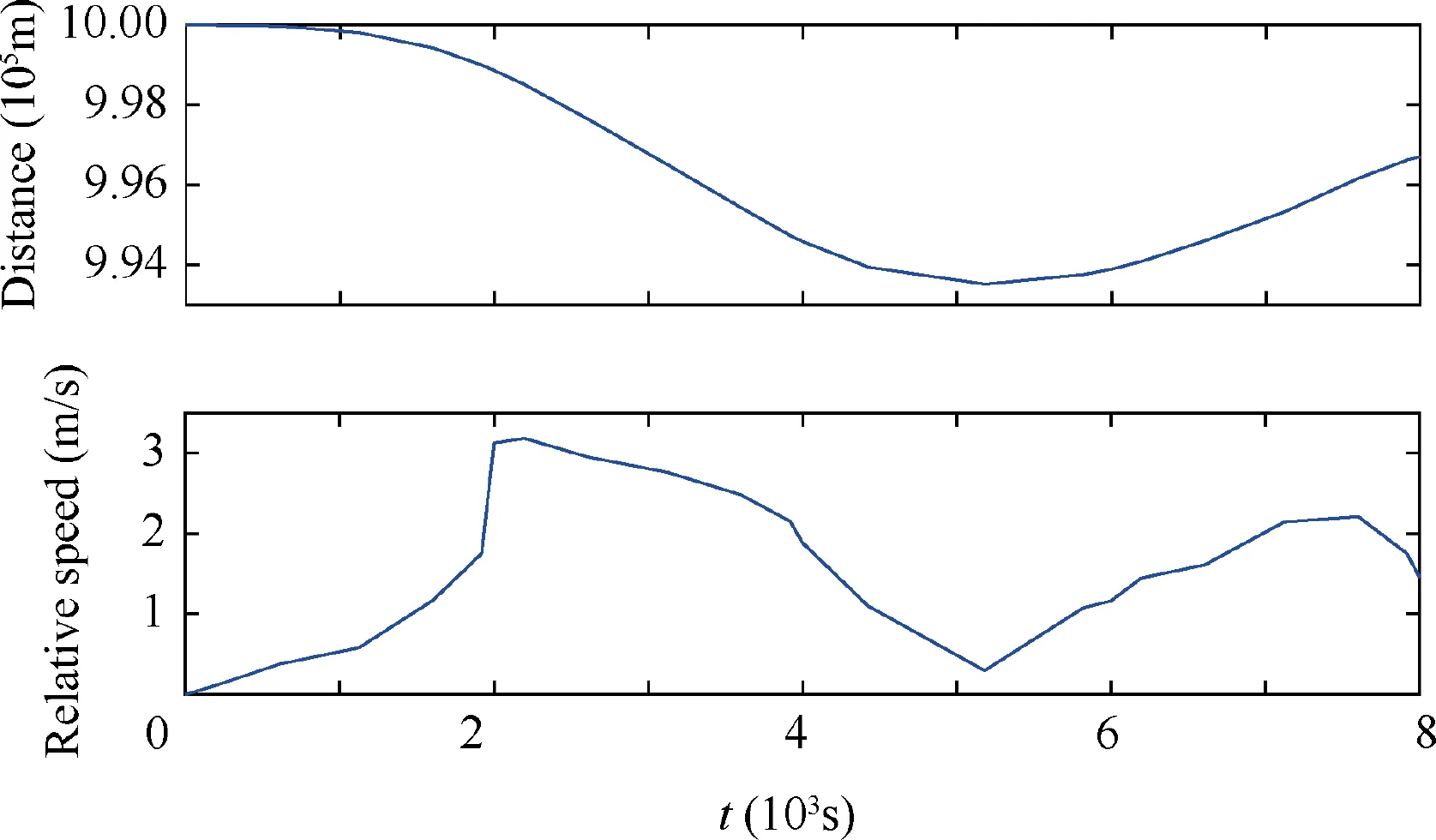
Fig.14 Relative distance and the motion speed between the end body and the main satellite.

subject to Eqs. (5) and (13) with the constant total tether length in PSE I and II.
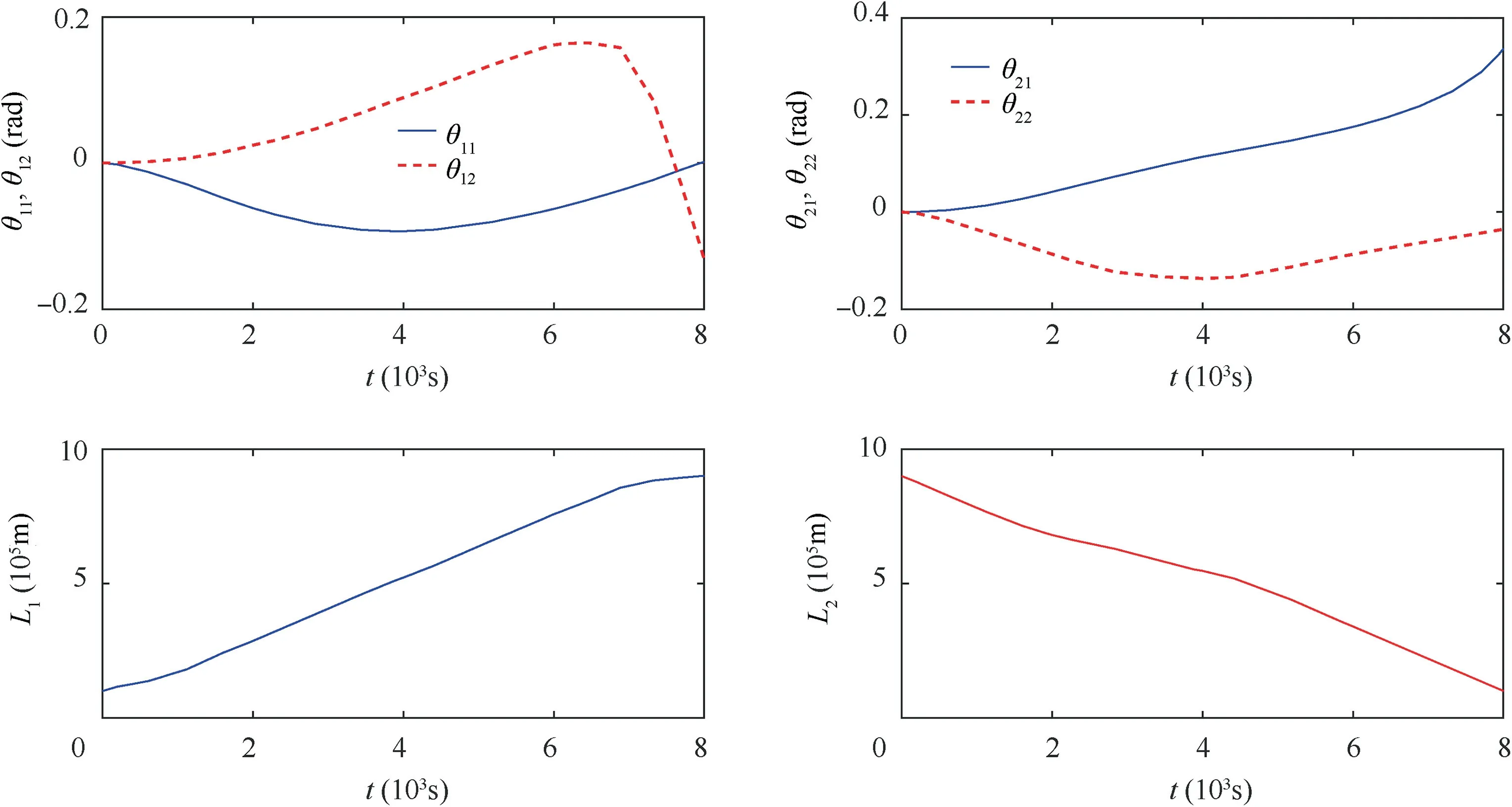
Fig. 15 Libration angles and tether lengths.
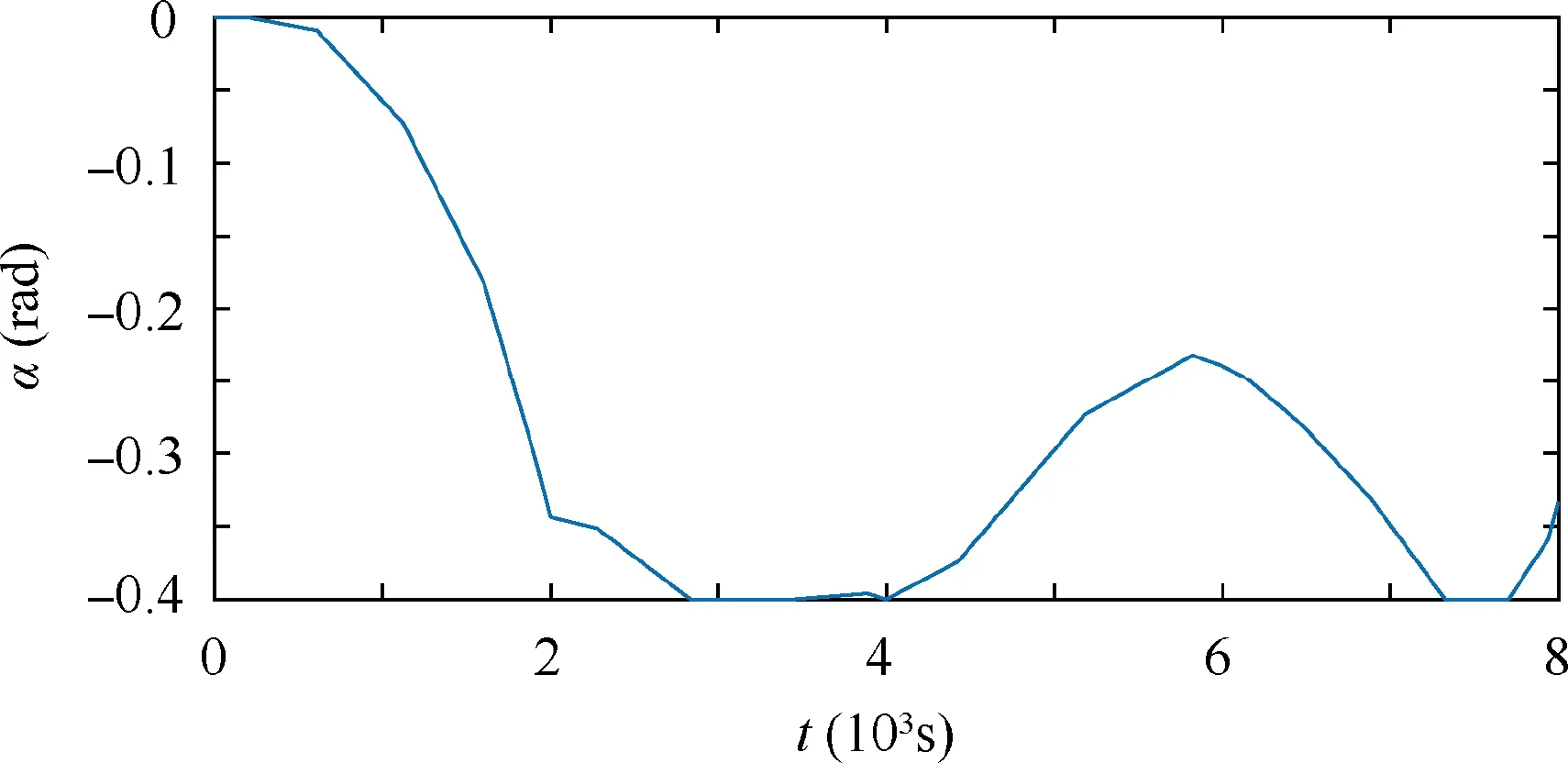
Fig. 16 Swing angles of the end body.
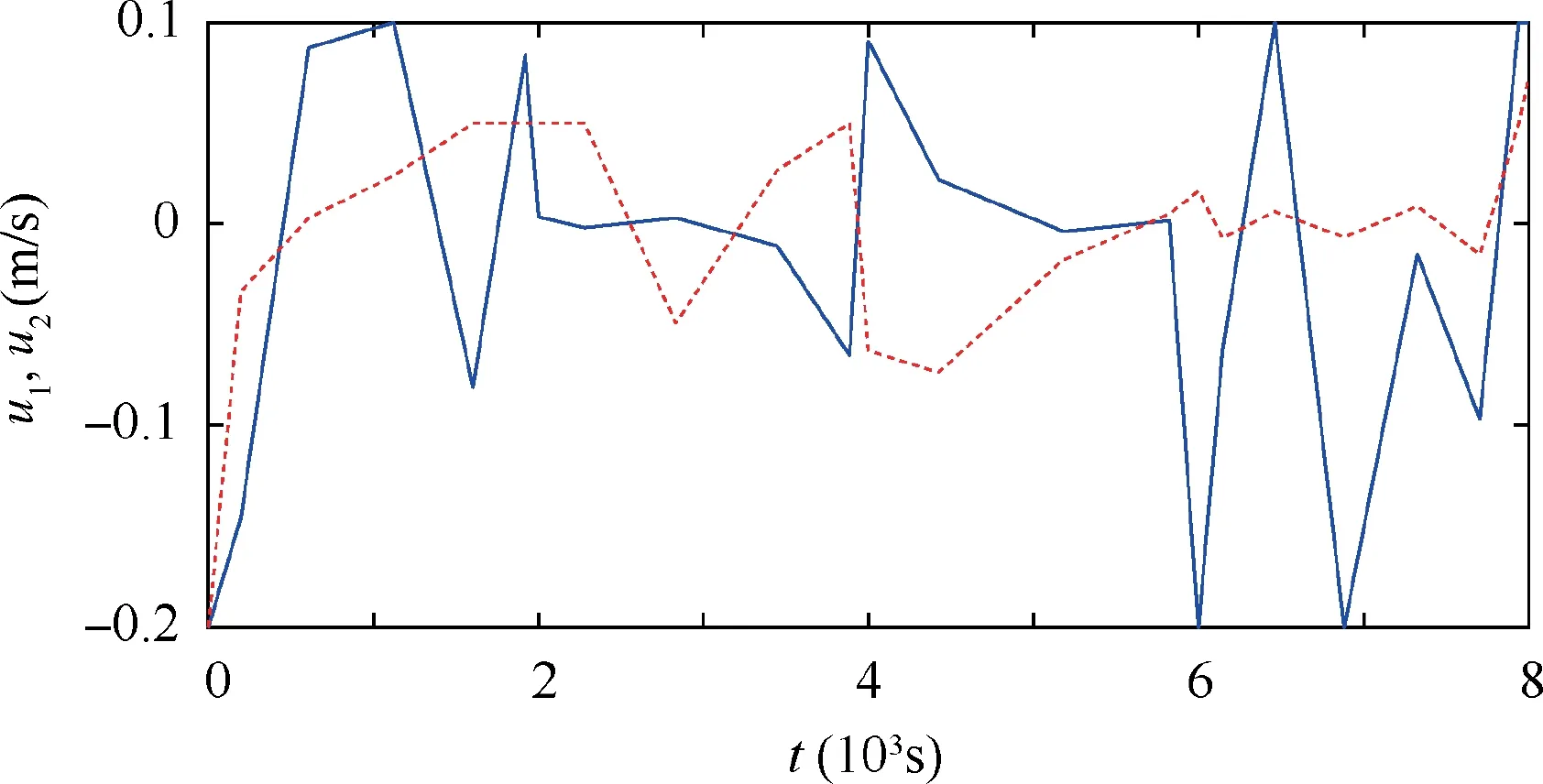
Fig. 17 Control inputs.
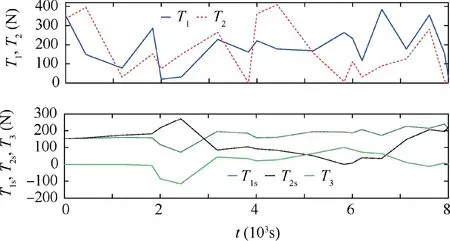
Fig. 18 Tensions in tethers and the internal force of the rod L3.
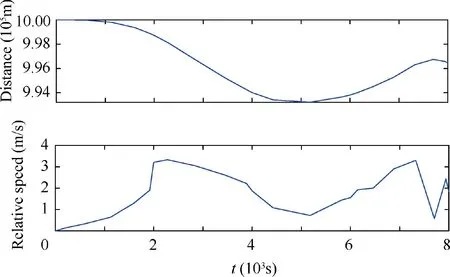
Fig.19 Relative distance and the motion speed between the end body and the main satellite.
The results are shown in Figs. 15-19. The swing of the end body in the transfer phase is shown in Fig.16.The attitude of the end body system α is bounded under the optimal control of the climber speeds. Initially, the α decreases from zero to -0.4 rad until 2700 s continuously. Then, in the following 1300 s, the α is kept near the lower bound. Fluctuations are observed in the period of 4000 s-8000 s. By the end of the transfer period, the approaches - 0.33 rad. Compared with the result in Case 1,the magnitude of α is smaller,see Figs.16 and 11.As shown in Fig.17,the control inputs fluctuate in the transfer period to keep the libration angles and the attitude angle in their bounds, as well as to limit the relative motion speed between the end body and the main satellite, see Fig.18,although the magnitudes of the control inputs in Case 2 are bounded. The effects of different control inputs in two cases can be observed in libration motions and lengths. By the end of the transfer phase, the residual θ11and θ12are 0 and 0.12 rad, respectively. The libration trends of PPSE II(θ21and θ22) are similar to the results in Fig. 10. Compared Fig. 10 with Fig. 15, it can be found that, the gaps between two cases are obvious, which corresponds to the differences between the control inputs in two cases. Tensions in tethers and the internal force of the rod L3are shown in Fig. 18.The results are similar to that in Fig.13 with a smaller magnitude of T2at the beginning. The distance and the relative motion speed between the end body and the main satellite are shown in Fig. 19. The results show that the magnitude of the relative motion speed is kept in the bound of[0,5 m/s]successfully by the controller.
In summary,by projecting the climbers’speed,the swing of the end body system can be stabilized well.The libration angles and relative motion speed between the main satellite and the end body can be either suppressed or exacerbated within the desired bounds. It should be noted that, the minimal gaps between the two tethers equal to the length of the rod due to the system shape in the give cases. However, in the case when the climbers I and II are moving upward and downward respectively,such gap should be considered to keep the tethers from collision for the system safety.
5. Conclusions
A dynamic model is developed for a parallel partial space elevator system, which is based on two parallel two-piece dumbbell models in favor of fast calculation and stabilization control analysis. The work investigates the effects of climber speed and mass ratio of climbers over end bodies on the libration of the PPSE system by considering three moving patterns of climbers. It reveals that
(1) The libration magnitudes of both the climber and the end body are propositional to the speed of climbers.
(2) The growth of the mass ratio of the climber over the end body increases the libration motion of the system.
(3) The swing of the end body system depends on the moving patterns and the swing could lead to the tumbling of PPSE if the climbers move in the opposite direction.Furthermore, the difference between two climbers will exacerbate the swing of the end body system.
(4) The attitude of the end body system in case of climbers moving in opposite direction is controllable by projecting moving speeds of climbers along tethers without thrust.
(5) The proposed control strategy suppresses the swing of the end body system effectively without sacrificing the efficiency of transport.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work is supported by the Discovery Grant(No.RGPIN-2018-05991)and Discovery Accelerate Supplement Grant(No.RGPAS-2018-522709) of Natural Sciences and Engineering Research Council of Canada, and Guangdong Basic and Applied Basic Research Foundation (No. 2019A1515111056)
Appendix A.


 CHINESE JOURNAL OF AERONAUTICS2021年3期
CHINESE JOURNAL OF AERONAUTICS2021年3期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Criteria for hypersonic airbreathing propulsion and its experimental verification
- Effect of scavenge port angles on flow distribution and performance of swirl-loop scavenging in 2-stroke aircraft diesel engine
- Ship detection and classification from optical remote sensing images: A survey
- Variational method based robust adaptive control for a guided spinning rocket
- Inertial parameter estimation and control of non-cooperative target with unilateral contact constraint
- Theoretical modeling of vectoring dual synthetic jet based on regression analysis
