Theoretical modeling of vectoring dual synthetic jet based on regression analysis

Zhijie ZHAO, Zhenbing LUO, Xiong DENG, Zhiyong LIU, Shiqing LI

College of Aeronautics and Astronautics, National University of Defense Technology, Changsha 410073, China

KEYWORDS Dual synthetic jet;Influence relation;Regression analysis;Theoretical model;Vector

Abstract The excellent vectoring characteristic of Dual Synthetic Jet(DSJ)provides a new control strategy for the active flow control, such as thrust vectoring control, large area cooling, separated flow control and so on. For incompressible flow, the influence relation of source variables, such as structure parameters of actuators,driving parameters and material attributes of piezoelectric vibrating diaphragm, on the vectoring DSJ and a theoretical model are established based on theoretical and regression analysis, which are all verified by numerical simulations. The two synthetic jets can be deemed as a main flow with a higher jet velocity and a disturbing flow with a lower jet velocity.The results indicate that the influence factors contain the low-pressure area formed at the exit of the disturbing flow, which could promote the vectoring deflection, and the impact effect of the disturbing flow and the suppressive effect of the main flow with the effect of restraining the vectoring deflection.The vectoring angle is a complex parameter coupled by all source variables.The detailed theoretical model,whose error is controlled within 3.6 degrees,can be used to quantitatively assess the vectoring feature of DSJ and thus to provide a guidance for designing the control law applied in the active flow control.

1. Introduction

Synthetic jet technology,with advantages of fast response,low energy consumption, lightness, no gas sources or pipelines,easiness to control and so on, has been considered as one of the most promising active flow control technologies nowadays.1At present, synthetic jet technology has been applied in many areas, such as thrust vectoring control,2-3enhancing blending and heat transfer,4-7restraining separated flow,8-13controlling the strength of shock waves14-16and so on, which has shown the brand applying prospect.

In the 1990s, Smith and Glezer17invented the first piezoelectric(PZT)synthetic jet actuator,composed of a cavity with a hole or seam and a PZT diaphragm. Although this actuator can realize the effective control of the flow field by forming reciprocating blow/suction jets, its disadvantages are listed:(A) Low energy efficiency. Half of the radiated sound energy is wasted with PZT diaphragm’s vibrating in both directions.Only around 10% of the energy is converted into the kinetic energy of jets.18(B) Easy failure of PZT diaphragms. When the pressure between controlled flow field and environment becomes larger and larger, PZT diaphragms will be difficult to activate or even fail. Dual Synthetic Jet Actuator (DSJA)has been invented,19which is composed of two cavities with holes or seams and a PZT diaphragm, which has not only the advantages of traditional Synthetic Jet Actuator (SJA)but also higher energy efficiency. A PZT diaphragm is shared by two cavities, which avoids the failure caused by excessive pressure difference between controlled flow field and environment. Dual Synthetic Jet (DSJ) is formed by the fusion of two jets and vectoring deflection could be realized by changing the ratio of two outlets. Moreover, wider ranges of vectoring deflection could be realized by controlling the relevant parameters, such as the driving parameters of PZT diaphragms and so on, which means that the vectoring deflection of DSJ can be controlled efficiently.18,20-23In addition to this, there have been many evidences that indicate that better control effect is able to be achieved by setting a certain angle between jets and controlled flow field in many areas,such as separated flow control, large-area heat dissipation and so on,18,24which means that DSJ with vectoring characteristic has a broader applying prospect. The best control effect of controlled flow field can be realized by controlling the range of vectoring deflection,based on different environments, which means that vectoring characteristic provides an excellent controlling channel for active flow control.

The vectoring characteristic of DSJ is affected by different parameters.Deng18,20-22has researched the effects of exit configuration,driving parameters of PZT diaphragms,exit length,exit pitch,exit depth,chamber height and exit width on vectoring DSJ. Wang et al.23has researched the influence of asymmetric cavities on vectoring characteristic. However, the above researches only explore the effects of single variable on vectoring DSJ based on numerical simulations and experiments. A complete theoretical model of vectoring DSJ, which can be used to evaluate or predict vectoring characteristic and further provide a law for the design of DSJA, has not been proposed.

Based on the deficiency of the above researches, influence relation of source variables on vectoring DSJ is established by theoretical analysis,which can be used to qualitatively evaluate its vectoring characteristic. Moreover, a detailed theoretical model is proposed to quantitatively predict vectoring angle and guide the design of DSJA, based on numerical simulations.

2. Influence factors of vectoring DSJ

The physical model of DSJA,containing the stages of blowing and sucking, is separately shown in Fig. 1(a) and (b). The width of exit 1 is smaller than exit 2. The fluid can be seen as incompressible because the Ma of DSJ is far less than 0.3.For incompressible fluid, the velocity of Exit 1 is higher than Exit 2 because the mass flow rate of two exits are identical.The jet with higher velocity is defined as main flow, while the jet with lower velocity is defined as disturbing flow. The detailed analysis will be started based on the influence of disturbing flow on main flow.

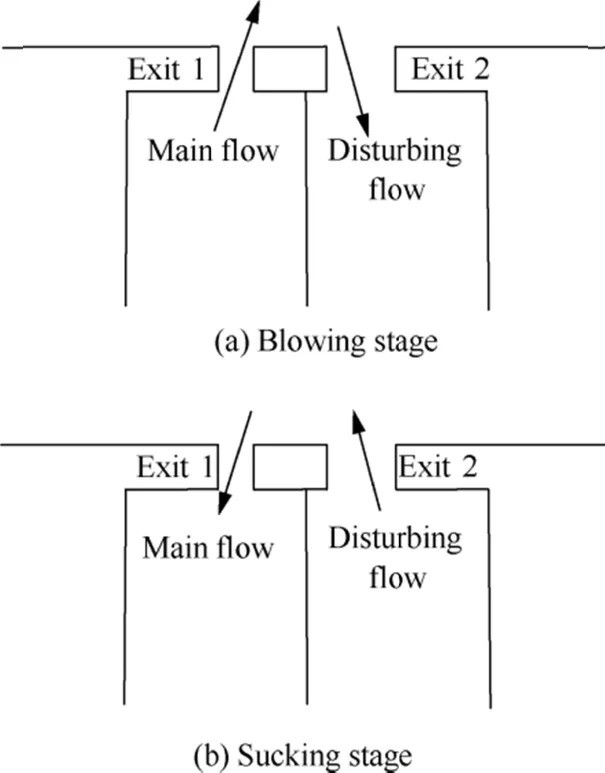
Fig. 1 Physical model of DSJA.

The velocities of two jets are separately defined as u1(t),u2(t), which satisfy cyclical relationships and can be expressed as

where uamp1,uamp2,f are respectively defined as the peak velocity of main flow at Exit 1,the peak velocity of disturbing flow at Exit 2 and the driving frequency of PZT diaphragms.

Air in DSJA’s cavity is incompressible, so the velocities of jets are connected with the volume velocity caused by diaphragms. Without considering the friction loss and local loss,uamp1, uamp2in the condition of simple boundary can be expressed as25

where κ is related to Poisson ratio of PZT diaphragms, and Am,Sc,SO1,SO2are separately defined as the amplitude of diaphragms,the area of cavities,the area of Exit 1 and the area of Exit 2. Relevant numerical expressions are shown as

where w1,w2,l,σ,D are separately defined as the width of Exit 1,the width of Exit 2,the length of exits,Poisson ratio of PZT diaphragms and the diameter of PZT diaphragms.

Based on Eqs.(5)-(7),Eq.(3)and Eq.(4)can be expressed as

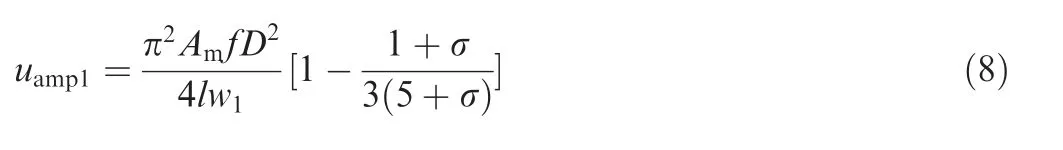
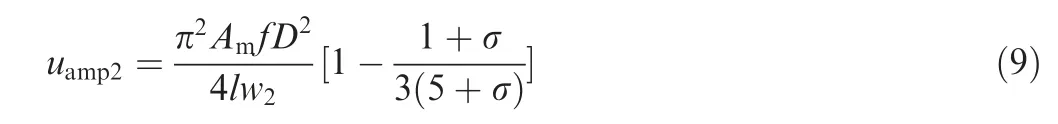
The strokes of main flow and disturbing flow L1, L2are defined as17

Based on Eqs. (1) and (2), Eqs. (10) and (11) can be expressed as

Based on Eqs. (8) and (9), Eqs. (12) and (13) can be expressed as

In the blowing stage of main flow, disturbing flow has a‘‘pull” effect on the main flow, which promotes to deflect the main flow to the side of the disturbing flow. Without the disturbing flow, main flow can be easily deemed as a synthetic jet and will not deflect. Thus, in the blowing stage, lowpressure area formed by the disturbing flow and the inertia of main flow are main influence factors.

In the sucking stage of Exit 1,disturbing flow is in the blowing stage. Meanwhile, the main flow formed in the last stage has removed far, so the sucking effect of Exit 1 will have no influence on main flow. However, the deflection of main flow will be restrained by the impact of disturbing flow. In this stage, the impact of disturbing flow on main flow is a key parameter influencing the vectoring characteristic.

2.1. Low-pressure zone

Low pressure is determined by pressure gradient ∇p, the area of low-pressure zone Apand the location of low-pressure zone Cp.26

∇p:By unsteady Bernoulli equation, the pressure relationship between the exit of the disturbing flow and far enough downstream can be obtained as

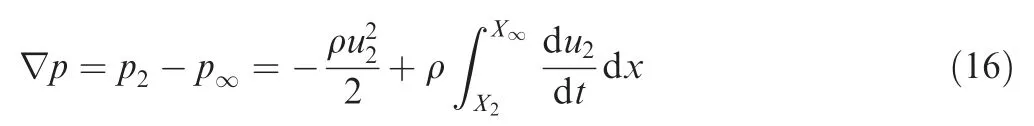
where variables with the subscript ‘‘2” represent the parameters of the Exit 2 and those with subscript ‘‘∞” represent the parameters of far enough downstream field,where the velocity of DSJ can be neglected.

The pressure gradient of low-pressure zone is directly controlled by 3 parameters, which are shown as follows:

(1) The momentum of disturbing flow M2

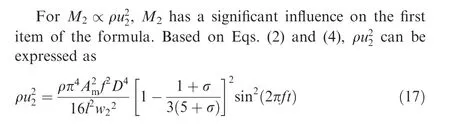
(2) Acceleration of disturbing flow a2

(3) Stroke of disturbing flow L2

L2is defined as the moving distance in the blowing stage of disturbing flow. Its expression is shown as

L2has a direct influence on the pressure gradient.

Based on the above analysis, ∇p can be expressed as

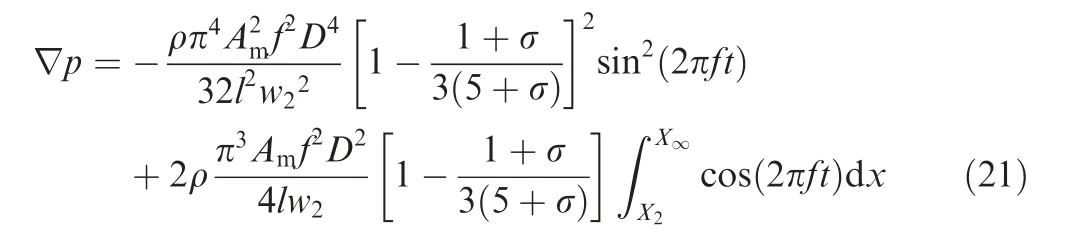
Apis decided by the length of low-pressure zone lpand the width of low-pressure zone wp.The width of vortex pair of disturbing flow R2is related to wp27.The relationship between R2and St is shown as

Based on Eqs. (22)-(24), the relationship can be expressed as

The area influenced by disturbing flow is related to lowpressure zone. Based on Eqs. (22)-(25), lpand wpcan be expressed as

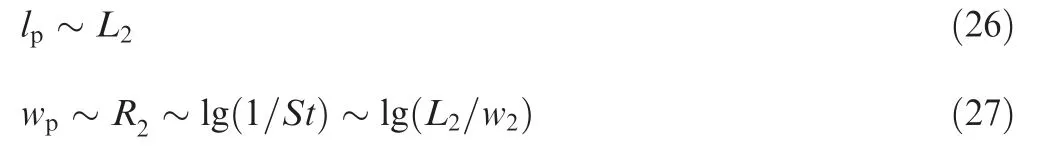
which show that Ap(lp,wp)is influenced by L2and w2.Based on Eq. (15), Eqs. (26) and (27) can be expressed as

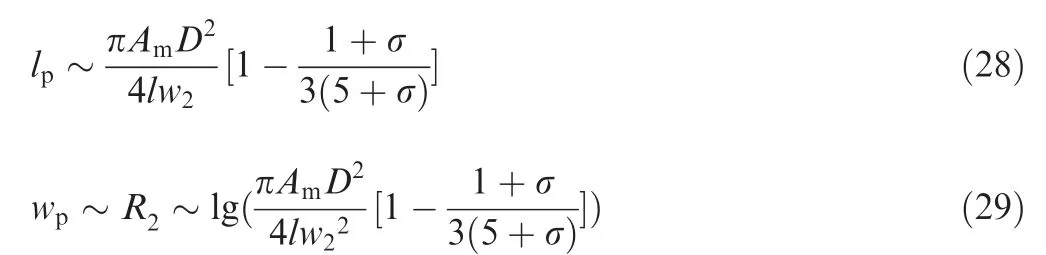
Cpis influenced by the distance between the two exits d,which can change the relative location of low-pressure zone,and then may have different effects on vectoring DSJ.The bigger d is, the more weakly it influences the vectoring characteristic. On the contrary, it will have a great influence on the vectoring characteristic, and even result in serious selfrecharging phenomenon.

2.2. Effect of inertia

In the blowing stage of main flow, the effect of main flow’s inertia can restrain the deflection. And in the sucking stage of main flow, the effect of disturbing flow’s inertia can also restrain the deflection. To evaluate the inertia of main flow and disturbing flow23, the energy of jet E1, E2are separately defined as

where Δp1is defined as the pressure difference between Exit 1 and interior cavity, and Δp2is defined as the pressure difference between Exit 2 and interior cavity.

State equations of ideal gas are shown as

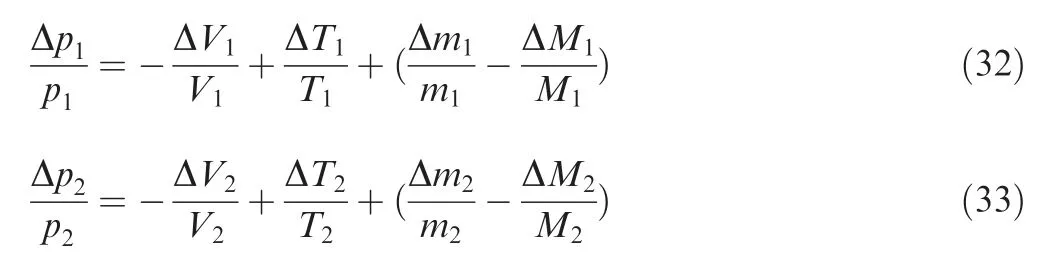
Ignoring the changes of temperatures and additional quality inputs, Eqs. (32) and (33) can expressed as

Based on the above analysis, E1, E2can be respectively expressed as

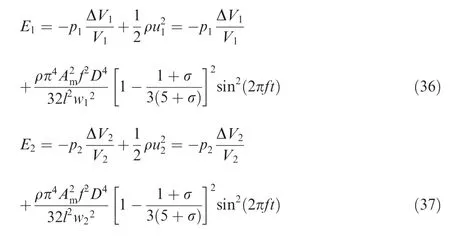
2.3. Influence relation of source variables on vectoring DSJ

The flow mode of jets in throats can also be influenced by the depth of exits h22,so h is also a source variable influencing the vectoring DSJ.

Amis depicted as

where U,φ are separately defined as the driving voltage of PZT diaphragms and the material attributes of PZT diaphragms. When single variable is U, Amis directly proportional to U if U is less than threshold voltage.

Above all, variables appearing in Eqs. (21), (28), (29), (36),(37), (38), d and h are influence factors of the vectoring DSJ.The structure parameters of actuators, the driving parameters of PZT diaphragms and the material attributes of PZT diaphragms are considered to be source variables,which indicates that the vectoring characteristic of DSJ is a parameter coupled by all source variables. The influence relation based on the above analysis is shown in Table 1. It is worth noting that the influence relation is established based on incompressible flow, so it is only appropriate for incompressible flow.

Based on the method proposed by Deng et al.20to evaluate the vectoring characteristic of DSJ, the vectoring angle of the DSJ θ can be expressed as

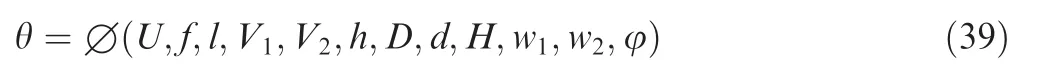
where the first two parameters are the driving parameters of PZT diaphragms, the third to ninth parameters are the structure parameters of DSJA, and the last one is a parameter corresponding to the material attributes of PZT diaphragms.

3. Establishment of theoretical model

Based on the results of numerical simulations, verify the rationality of influence relation of source variables on vectoring DSJ and induct the detailed theoretical model of the vectoring DSJ by regression analysis.

3.1. Physical model of DSJA

The results of three-dimensional numerical simulations show that an actuator with an exit aspect ratio of 4 has a twodimensional flow field characteristics in the middle of the exit.The exit aspect ratio of actuator using in this part is 10,so twodimensional numerical simulations are appropriate. The physical model of DSJA is shown in Fig.2 and the relevant parameters are listed as follows: d=5 mm, h=4 mm H=7 mm,D=46 mm, w1+w2=4 mm.

3.2. Computational method

For fully displaying the dynamic flow field, set the area of the calculation domain as 350 mm×200 mm, which can display the flow field clearly. Based on the pressure-based solver, the relevant functions—continuity equation and incompressible Reynolds averaged N-S equation—are expressed as

Table 1 Influence relation of source variables on vectoring DSJ.

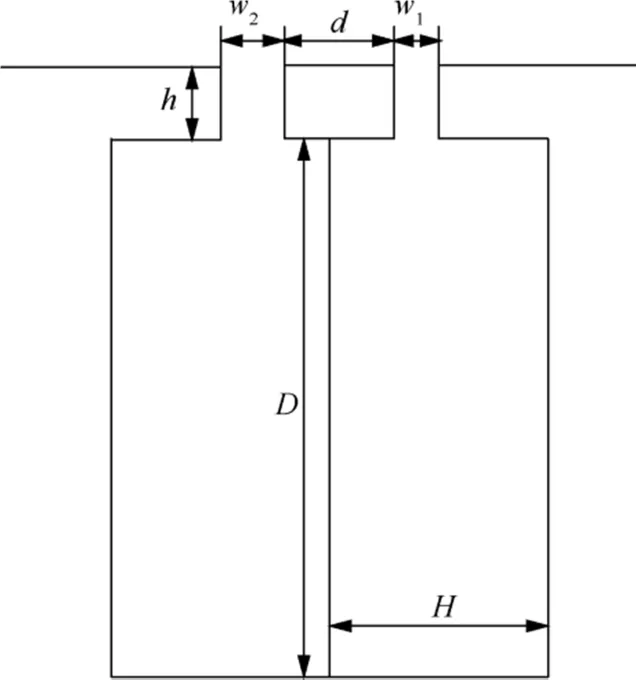
Fig. 2 Physical model of DSJA.

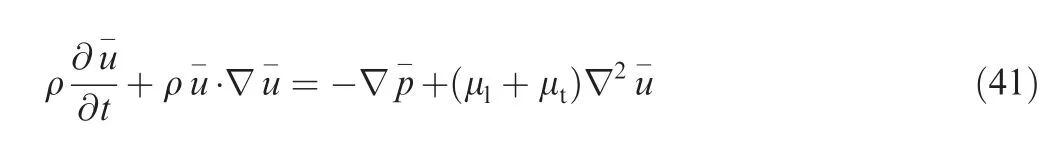
where μland μtare separately defined as the viscosity coefficient of laminar flow and turbulent flow.

The PISO algorithm is applied to deal with the coupling of pressure and velocity. Momentum and energy equations are discretized by a second-order upwind style, and time discretization is realized by a second-order implicit scheme. The convergence criterion is that the relative error is less than 10e-5. In addition, the time step is 1/80 of the cycle, and the maximum iterations per step are set as 50 steps, and the total time of the simulation is set as 100 cycles,which can ensure the correctness of final results.

Treat the actuator and the external flow field as a single connected area. The boundaries of the external flow field are set as pressure-outlet boundary and the walls of cavities are set as no slip wall. The surfaces of PZT diaphragms are set as velocity-inlet boundaries.Based on X-L model28,neglecting the change of curvature, the normal velocities are set as

The verification of grid independence and turbulence model based on experimental data25is shown in Fig. 3. DSJ’s flow field is mainly determined by the jet velocity at DSJA’s exit,so the optimal grid and turbulence model is chosen by comparing jet peak velocity at exit. Three kinds of grid, which are all structured and orthogonal, and two different turbulence models are compared with experimental data,and the results show that SST k-ω model has larger error than RNG k-ε model,and when the number of grids exceeds 98700, the error almost maintains constant. So RNG k-ε model is used to simulate the flow field of DSJ, which could simulate jet impact, separated flow, secondary flow and other complex problems well.The total number of grids is set as 98,700 and the distribution of grids at exits is shown in Fig. 4. Based on this computational method, the vectoring DSJ’s flow field is simulated, in which the relevant parameters are set as U0=0.60 m/s,f=550 Hz, w2/w1=1.5:2.5, and its result is compared with experimental data21(Fig. 5). The result of numerical simulation (Fig. 5(a)) shows higher dissipation rate in downstream flow field, but great consistence with experimental data(Fig. 5(b)) is shown in core area,20which means that θ does not have great difference.θ of numerical simulation and experimental data are respectively 15.54 and 14.97.The error is less than 1 degree, so it is appropriate to use this computational method to do the following researches.

3.3. Results and analysis

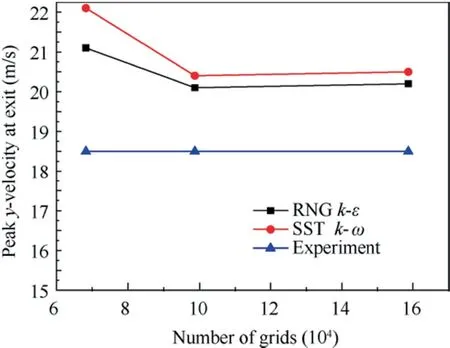
Fig. 3 Comparison among different grids and turbulence models.

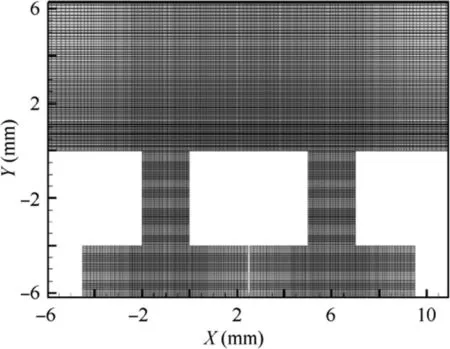
Fig. 4 Distribution of grids.

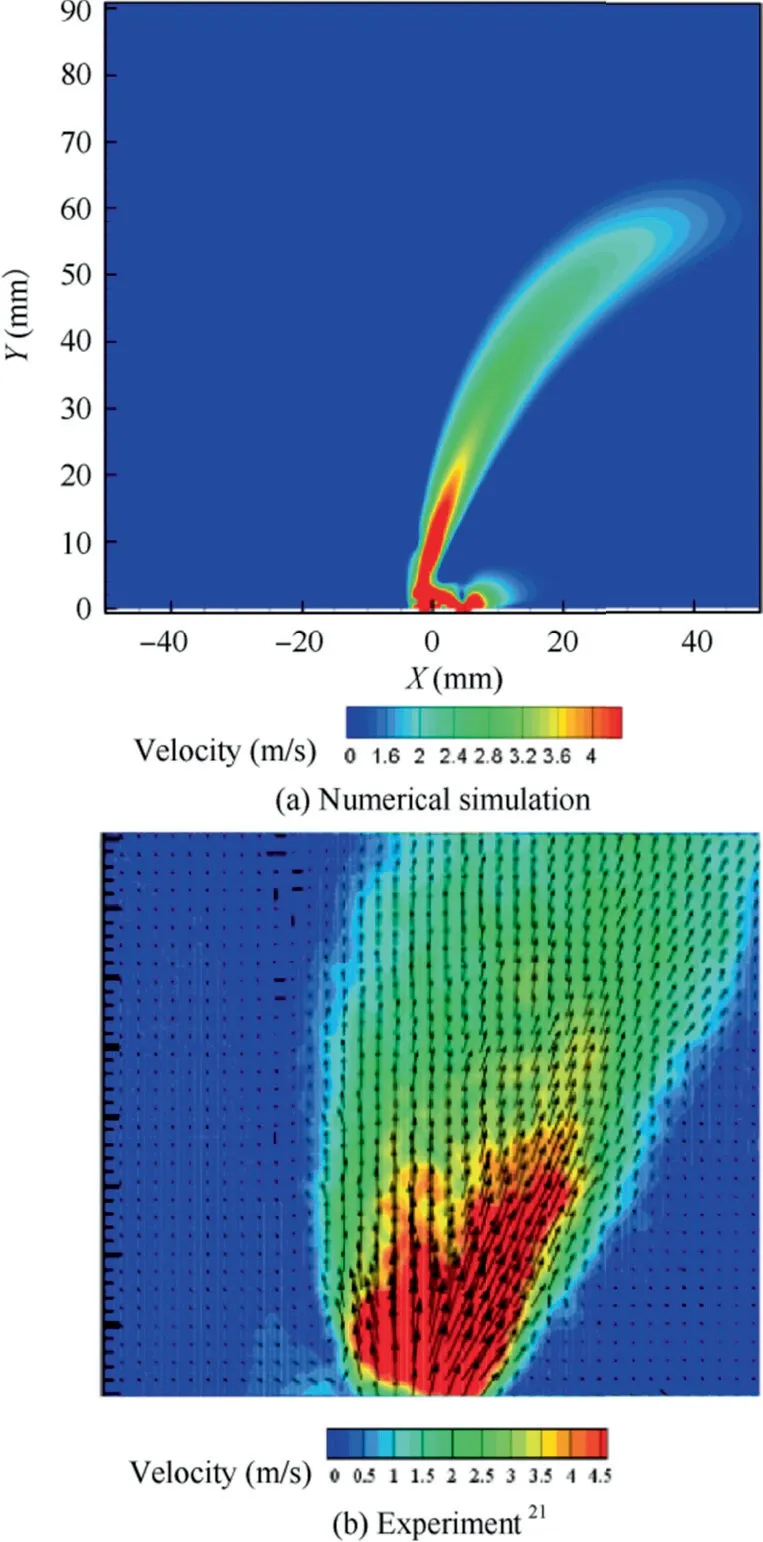
Fig. 5 Comparison between numerical simulation result and experimental data.

The schemes of cases and results are shown in Table 2. The vectoring angle is calculated by the method proposed by Deng et al.20.Case 1-Case 7 are set to explore the influence of w2/w1in the condition that f, Amare kept unchanged. Case 8- Case 11 are set to research the influence of increasing Amin different w2/w1in the condition that f,whose value is the same as Case 1- Case 7, is kept constant. Case 12-Case 15 are set to explore the effect of decreasing f and increasing Amin different w2/w1in the condition that U0(2πfAm) is unchanged, whose value is kept the same as Case 1-Case 7. Case 3, Case 9, Case 16-Case 18 are set to explore the influence of Amin the condition that f,w2/w1are kept unchanged. Case 3, Case 19-Case 22 are set to explore the influence of f in the condition that Am, w2/w1are kept unchanged.

|∇p|, L2, lg(L2/w2), E1, E2are calculated for analyzing the influence relation and induct detailed theoretical model,which are shown in Table 3.The physical variables with subscript‘‘1”represent the parameters of main flow and those with subscript‘‘2” represent the parameters of disturbing flow.

Case 1-Case 7 are analyzed to explore the influence of w2/w1, and the trends of |∇p|, L2, lg(L2/w2) , E1, E2and θ are shown in Fig.6.What’s more,the contours of average velocity in every state are shown in Fig.7.In this process,U0,f,Amare separately set as 0.68 m/s, 500 Hz, 0.216 mm, and the only variable is w2/w1.How |∇p|, L2, lg(L2/w2) , E1, E2influence θ is analyzed by changing w2/w1from 5.67 to 1.

When w2/w1equals 5.67,the main flow is influenced by the disturbing flow and vectoring deflection happens. In this status, E1gets the maximum, while Ap(L2, lg(L2/w2)) get the minimum, which can restrain the deflection. E2gets the minimum,and it can promote the deflection.θ remains 7.49 degrees in these factors.It is worth noting that a big circulation zone is formed in the direction of deflection. In this state (Fig. 7(g)),main flow has the highest energy,so it has great ejection effect on disturbing flow. At the same time, the low-pressure area formed at Exit 2 has sucking effect on main flow, and makes the main flow deflect to the side of low-pressure area in the downstream flow field, which gets the circulation zone established.25Similar phenomenon also happens when w2/w1=4(Fig. 7(f)). Then, with the fall of w2/w1, E2increases and ∇p decreases, which can retrain the deflection. Meanwhile, Aprises and E1drops, which can promote the deflection. In this period, the function of restraining dominates, which results in the fall of θ. These factors balance when w2/w1equals 2.33, and θ equals 1.5 degrees. In this state (Fig. 7(e)), the direction of velocity of the core area is almost vertical, which mainly is due to the rise of impact effect of disturbing flow on main flow, so θ is very small. Then, with the decrease of w2/w1, the promotion caused by the rise of Ap,∇p and the dip of E1dominates compared with the restraining function caused by the increase of E2, which results in the rise of θ.When w2/w1equals 1.67,θ gets the maximum of 10.65 degrees.In this state, the direction of velocity of core area has great deflection,which is shown in Fig.7(d).Then,with the decrease of w2/w1, the restraining function caused by the increase of E2dominates compared with the promotion caused by the rise of Ap,∇p and the decrease of E1, which results in the drop of θ.When w2/w1equals 1.5, θ equals 6.58 degrees. Then, with the decrease of w2/w1, the promotion dominates, which can result in the increase of θ. When w2/w1equals 1.35, θ rises to 7.29 degrees. Obvious evolution process of flow field is shown in Fig. 7(b), (c), and (d). Then, with the decrease of w2/w1, the restraining function dominates, which can result in the drop of θ.When w2/w1equals 1,θ decreases to 0 degree.In this state(Fig. 7(a)), the flow field shows great symmetry, which means that the impact effect and sucking effect are consistent,so θ is 0 degree.

Table 4 shows that the rates of relative changes of|∇p|,L2,lg(L2/w2),E1,E2and θ in each changing process,which shows that the relationship between θ and relevant physical variables is not a simple linear relationship and the sensitivities of θ torelevant physical variables are in reference to the values of w2/w1.

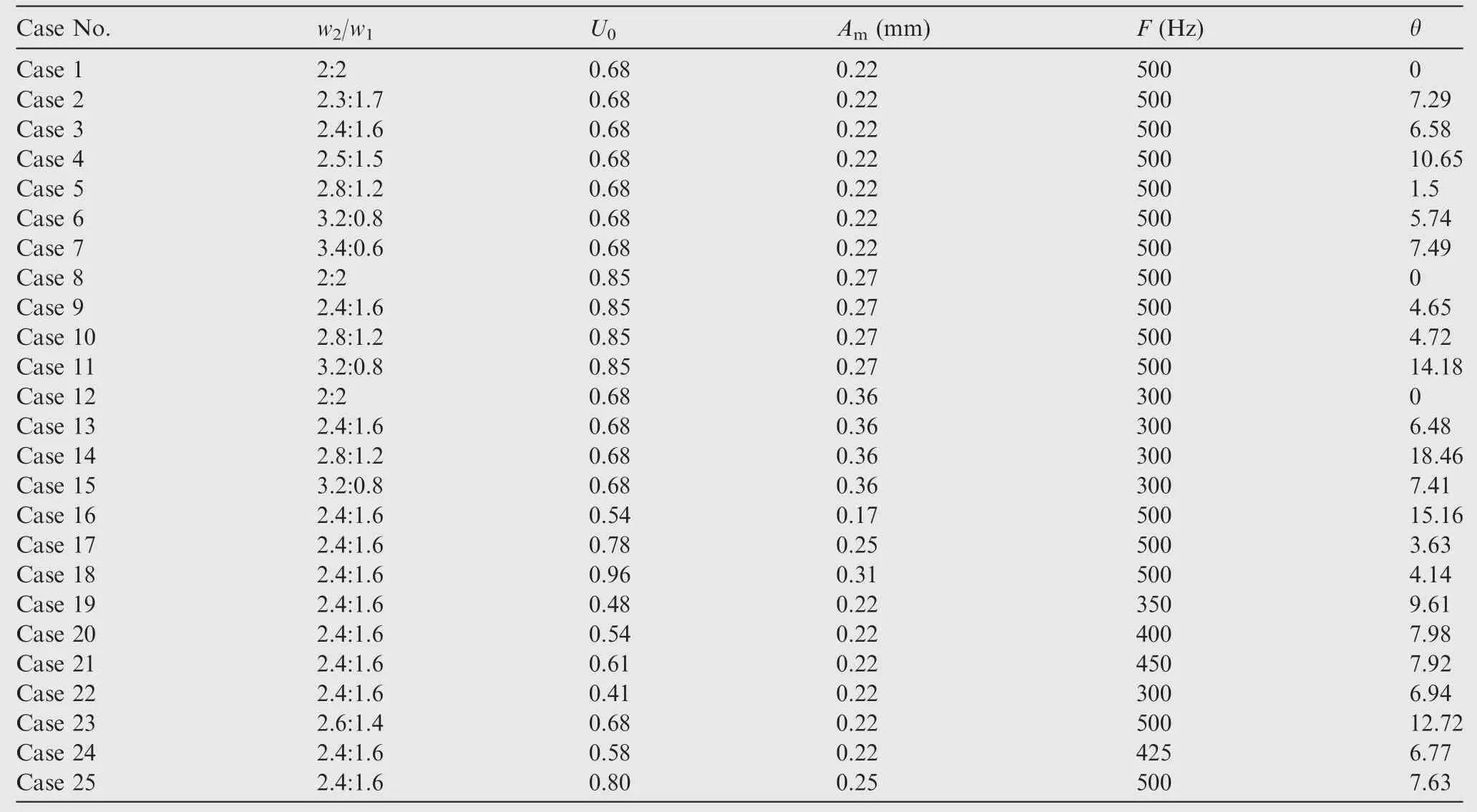
Table 2 Computational cases for DSJA.

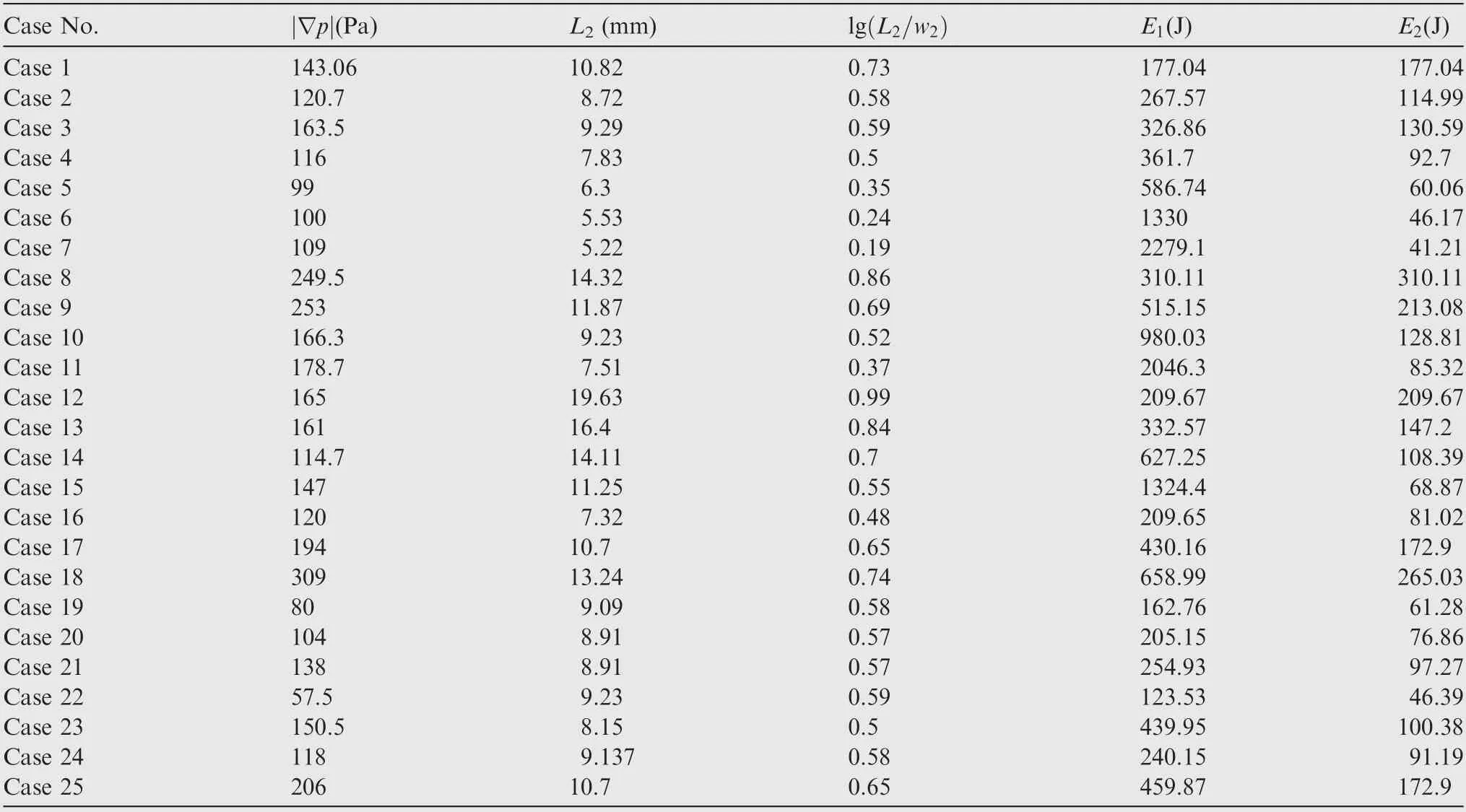
Table 3 Results of cases.

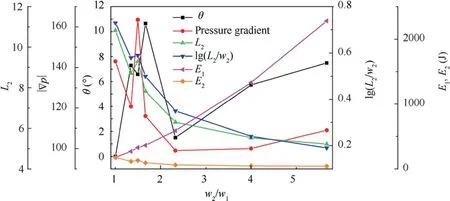
Fig. 6 Trends of |∇p|, L2, lg(L2/w2) , E1, E2 and.θ

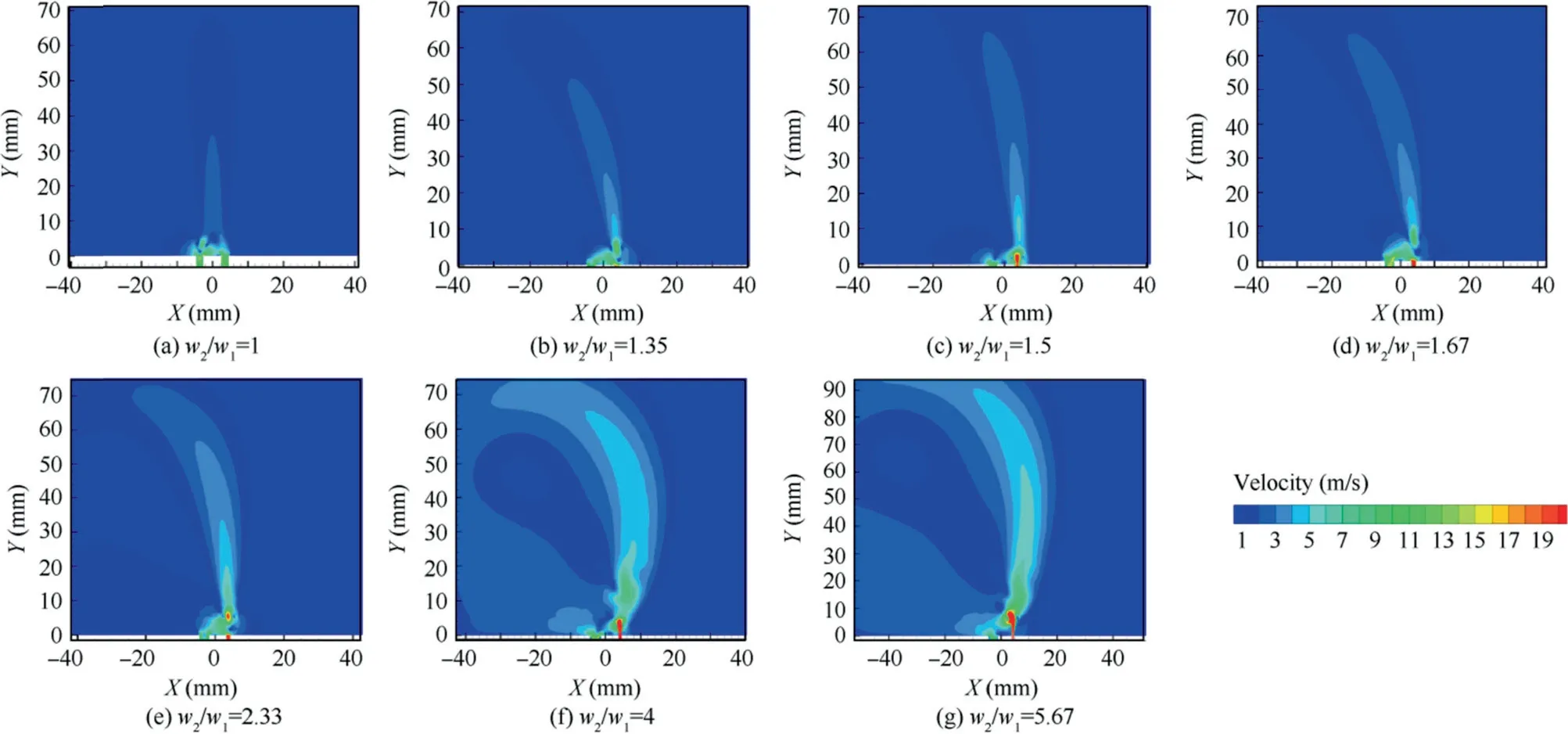
Fig. 7 Contours of average velocity of Case 1- Case 7.

Case 8-Case 11 are analyzed to explore the influence of Amby increasing the original value 0.22 to 0.27 and keeping f unchanged, which is the same as Case 1-Case 7, and the rates of relative changes of|∇p|,L2,lg(L2/w2),E1,E2and θ in different values of w2/w1compared with Case 1-Case 7 are shown in Fig.8.Moreover,the contours of average velocity of Case 8-Case 11 are shown in Fig. 9.

Increase U0,and make the value of f remain the same,which means increasing the value of Am. When the value of U keeps less than saturated driving voltage,the value of U will increase linearly.In these cases,|∇p|,L2,lg(L2/w2),E1and E2all increase. When w2/w1equals 1.5, the restraining functioncaused by the rise of E1and E2dominates compared with the promotion caused by the increase of Apand∇p, which results in the drop of θ.In this state(Fig.9(b)),main flow almost does not deflect until getting to a certain location 35 mm away from the exit and its energy is very low.It is worth noting that weak self-recharging phenomenon happens between Exit 2 and Exit 1 because of the increase of sucking effect on main flow,which also results in lower energy of core area. When w2/w1equals 2.33 or 4, the promotion caused by the increase of Apand∇p dominates compared with the restraining function caused by the rise of E1and E2,which results in the increase of θ.In these states (Fig. 9(c), (d)), circulation zone also forms due to the enhancement of sucking effect on main flow. Apart from this,sensitivities of θ to relevant physical variables are in reference to the values of w2/w1, Am.

Table 4 Rates of relative changes.

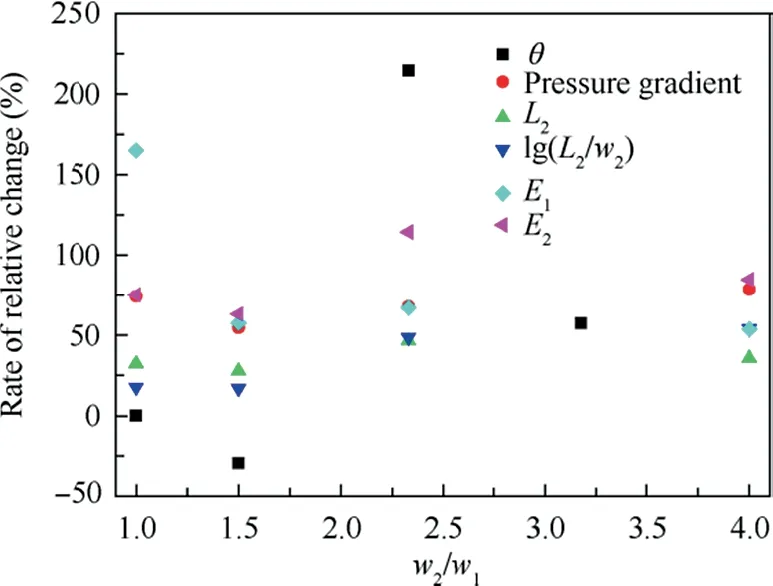
Fig. 8 Rates of relative changes of |∇p|, L2, lg(L2/w2) , E1, E2 and θ in different values of w2/w1 with Case 1 - Case 7.

Case 12-Case 15 are analyzed to explore the influence of coupled parameters by only decreasing f from 500 Hz to 300 Hz,and keeping U0the same as Case 1-Case 7,which also means that Amwill increase. The rates of relative changes of|∇p|, L2, lg(L2/w2) , E1, E2and θ in different values of w2/w1compared with Case 1-Case 7 are shown in Fig.10.In addition, the contours of average velocity of Case 12-Case 15 are shown in Fig. 11.

Decrease f, and make the value of U0remain unchanged,which means increasing Amand keeping fAmconstant. ∇p,Ap(L2, lg(L2/w2)) and E2all increase and E1does not change much. When w2/w1equals 2.33 or 4, the promotion caused by the increase of Apand∇p dominates compared with the restraining function caused by the rise of E2, which results in the significant increase of θ. In these two states, due to the enhancement of sucking effect on main flow, main flow does not have enough energy to get over the sucking effect and continue to spread downstream,which also causes the decrease of area of circulation zone. Obviously, in flow field (Fig. 11(c),Fig. 11(d)), the distance that main flow can reach is less than 40 mm. The weak self-recharging phenomenon happens at exits and this is mainly because of the enhancement of the strength of the low-pressure area. When w2/w1equals 1.5,the promotion caused by the increase of Apand∇p is balanced by the restraining function caused by the rise of E2, which makes θ basically unchanged. In this state (Fig. 11(b)), the stroke of main flow decreases and a circulation zone forms compared with Case 3, which is mainly due to the rise of the sucking effect on main flow. In addition, sensitivities of θ to relevant physical variables are in reference to the values of w2/w1, Amand f.

Overall, the vectoring characteristic of DSJ can be qualitatively evaluated and analyzed by the influence relation of source variables on vectoring DSJ established in Section 2.Moreover, θ is a complex function of |∇p|, L2, lg(L2/w2), E1and E2and the sensitivities of θ to these physical variables vary with the values of source variables.

3.4. Theoretical model of vectoring DSJ

Based on influence relation established in Section 2, the relationship between θ and relevant physical variables can be expressed as

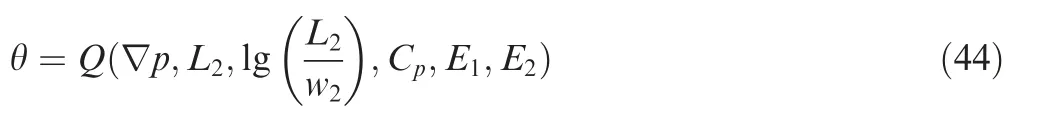
where Cpis a constant in numerical cases,so it will not be considered in subsequent analysis.

Because of the great difference existing in the ranges of data in Section 3, for decreasing the prediction error, the normalized processing is applied and its expression can be written as

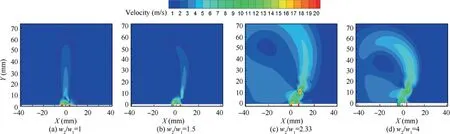
Fig. 9 Contours of average velocity of Case 8-Case 11.

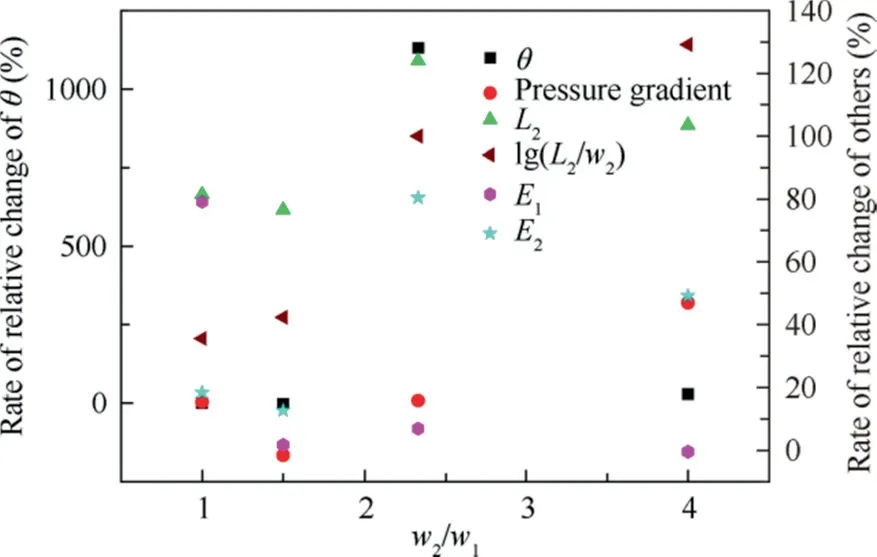
Fig. 10 Rates of relative changes of|∇p|, L2,lg(L2/w2) , E1, E2 and θ in different values of w2/w1 with Case 8 - Case 11.

Based on the data in Section 2 and Section 3, the detailed theoretical model will be built by multiple nonlinear regression. Based on limited data, considering that the sensitivities of the vectoring angle to each physical variable are complex parameters related to all source variables, the theoretical model will only consider single source variable.

Based on data in Section 2 and Section 3,when w2/w1,Am,f are separately viewed as a single source variable, the theoretical model can be expressed as

where v is defined as a source variable.And|∇p|,L2,lg(L2/w2) , E1, E2can be respectively calculated by Eqs. (21), (15),(36) and (37).

When the single source variable is separately set as w2/w1,Amor f, the comparison between predicted data calculated by the theoretical model and real data is displayed in Fig. 12 and the average training error is respectively 18.46%, 5.43%,6.94%, which are all within the controlled ranges. The test results of generalization abilities of the theoretical model are displayed in Table 5, which shows that the error is controlled within 3.6 degrees and the rationality of the theoretical model is also verified to some extent.

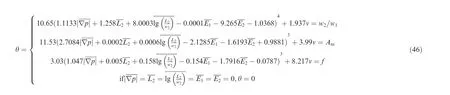
Fig. 11 Contours of average velocity of Case 12-Case 15.

Fig. 12 Comparison between predicted data calculated by theoretical model and real data.

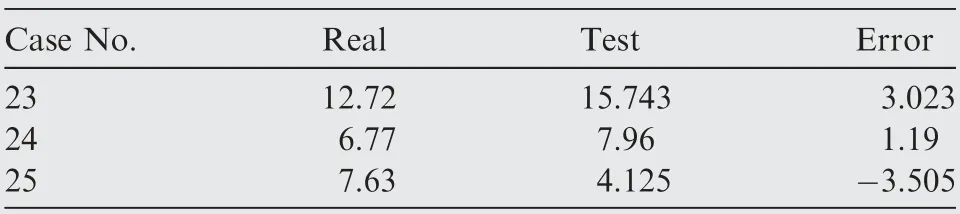
Table 5 Comparison between real data and test results.

4. Conclusions

For incompressible flow, the influence relation of source variables on vectoring DSJ was analyzed and numerical simulations were carried out to verify the rationality of the influence relation and induct the detailed theoretical model of the vectoring DSJ. The specific conclusions and prospects were as follows:

(1) The influence relation of source variables on vectoring DSJ was analyzed. The low-pressure area formed by the disturbing flow, the inertia of main flow and disturbing flow were considered to be influence factors.And the structure parameters of actuators, the driving parameters of PZT diaphragms and the material attributes of PZT diaphragms were considered to be source variables. The vectoring angle of DSJ was a complex parameter coupled by all source variables.

(2) Based on numerical simulations, the rationality of the influence relation was verified. Moreover, the detailed theoretical model was built based on single source variable w2/w1, Amand f by multiple nonlinear regression.The test results of generalization abilities showed that the error was controlled within 3.6 degrees. In addition to this, the theoretical mode had certain physical meanings.

(3) The sensitivity of θto relevant physical variables is a complex function of all source variables,but the theoretical model built in this paper is only an average result by fitting, only considering a single source variable. The whole and more accurate theoretical model is lacked.In the next step, a database of DSJ’s vectoring characteristic will be established by combining numerical simulations with PIV, and the optimal high-precision theoretical model will be obtained through machine learning.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors thank the members of AFC&APP Laboratory for their advice to model and simulate. This research was supported by the National Natural Science Foundation of China(Nos. 11972369 and 11872374).