Proactive optimization of transmission power and 3D trajectory in UAV-assisted relay systems with mobile ground users

Jingchun GU, Guoru DING,*, Yito XU, Hicho WANG, Qihui WU

a School of Communications Engineering, Army Engineering University of PLA, Nanjing 210007, China

b School of Electronic and Information Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

KEYWORDS Outage probability;Primal-dual subgradient;Proactive optimization;Successive convex approximation;Unmanned Aerial Vehicle(UAV) relay

Abstract In this paper,an Unmanned Aerial Vehicle(UAV)-assisted relay communication system is studied, where a UAV is served as a flying relay to maintain a communication link between a mobile source node and a remote destination node.Specifically,an average outage probability minimization problem is formulated firstly,with the constraints on the transmission power of the source node, the maximum energy consumption budget, the transmission power, the speed and acceleration of the flying UAV relay. Next, the closed-form of outage probability is derived, under the hybrid line-of-sight and non-line-of-sight probability channel model. To deal with the formulated nonconvex optimization,a long-term proactive optimization mechanism is developed.In particular,firstly,an approximation for line-of-sight probability and a reformulation of the primal problem are given,respectively.Then,the reformulated problem is transformed into two subproblems:one is the transmission power optimization with given UAV’s trajectory and the other is the trajectory optimization with given transmission power allocation.Next,two subproblems are tackled via tailoring primal-dual subgradient method and successive convex approximation, respectively. Furthermore,a proactive optimization algorithm is proposed to jointly optimize the transmission power allocation and the three-dimensional trajectory. Finally, simulation results demonstrate the performance of the proposed algorithm under various parameter configurations.

1. Introduction

1.1. Background and motivation

UAV, also called drone, has been widely applied in various areas due to its unique advantages such as high mobility,low cost and flexible on-demand deployment. Recent example applications of UAV consist of emergency search and rescue,environmental monitoring, wireless communication and so on.1-5In particular, in the wireless communication field,UAV not only can be used as a flying base station to provide fast access for terrestrial users, but also can be dispatched to relay information between spatially separated nodes.6-13

Recently, UAV-assisted relay communications have received increasing research attentions. However, majority of the existing studies related to UAV-aided relay system focus on static users on the ground, which are not suitable for dynamic ones, such as the mobile vehicles. For example, in remote areas, the communication facilities may have not been constructed. In urban areas, the communication facilities may be damaged due to natural disasters. In these cases, UAV can be served as a flying relay to maintain communication links between mobile ground vehicles and remote users, where the mobile vehicles move to the destination according to their equipped navigators. Secondly, the range of motion of the UAV will increase with the movement of the vehicles, which results in a corresponding increase of UAV energy consumption. Thus, it is necessary to carefully control the UAV’s Three-Dimensional (3D) flight trajectory considering the fact that the UAV is generally energy-limited.14-17Thirdly, communication reliability of a flying UAV relay in the whole mission time is one of the key indicators, which can be measured by minimizing the average outage probability during a period of time.These observations motivate us in this paper to investigate the issue of average outage probability minimization problem for UAV-assisted relay communication system with mobile ground users.

1.2. Related work

During the past few years, there have been quite a few studies on UAV-assisted relay communication in the existing literature. Compared with conventional static relay, UAV-assisted relay shows new characteristics due to its higher altitude and mobility.11,18Channel modeling and performance analysis were studied in Refs.19-21for UAV-assisted relay systems.For example, the authors in Ref.19provided a survey for the UAV channel characterization with measurement campaigns and statistical channel models. In Ref.20, the UAV’s heading angles were designed to improve the communication performance. Generally, throughput and reliability are two key indicators in UAV-assisted relay system. Specifically, in Ref.10, the authors investigated a throughput maximization problem for a UAV-enabled Decode-and-Forward (DF) relay system. The authors in Ref.22considered a spectrum sharing planning problem with the aim of maximizing sum throughput for a full-duplex UAV relaying system with underlaid deviceto-device communications. The work of Ref.12considered an outage probability minimization problem for UAVenabled Amplify-and-Forward(AF)relay system.The authors of Ref.23studied the overall outage probability minimization problem, where the full-duplex DF technique was used for UAV-enabled relay system. In Ref.24, the authors measured the total power loss, the overall outage, and the overall bit error rate with the aim of maximizing reliability of UAVassisted relay system.

Parameter optimization is a dominating research issue in the existing studies.For instance,in Refs.10,12,22,23,the UAV’s trajectory and power allocations were jointly optimized to achieve their objective functions.In Ref.24,the UAV’s altitude was optimized for maximum reliability in UAV-assisted relay system. In Ref.25, a joint resource optimization for sensing time,node powers,and the number of clusters was formulated to maximize the average total throughput in Cognitive Industrial Internet of Things (CIIoT) system. Furthermore, the authors in Ref.26jointly optimized beamforming, power allocation, circular radius and flight speed to maximize the energy efficiency in a UAV-enabled AF relay system.Note that the existing studies about UAV-assisted relay systems mainly focus on the reactive parameter optimization methods, which are step-by-step or point-by-point in essence.Moreover, majority of the existing studies focus on the static ground nodes,which cannot be directly applied to general scenarios where dynamic nodes exist, such as mobile vehicles.Last but not the least, UAV’s two-dimensional trajectory is optimized but 3D trajectory is ignored in the existing UAV-assisted relay system,especially related to outage probability problem.

1.3. Contributions and organization

In this paper, we investigate an average outage probability minimization problem for UAV-assisted relay communication system, where a UAV is served as a flying relay to maintain a communication link between a mobile source node and a remote destination node.In particular,the main contributions of this paper are summarized as follows:

(1) The average outage probability minimization problem for UAV-assisted relay communication system.An average outage probability minimization problem is investigated, subject to the constraints including the source node and UAV’s transmission power,UAV’s maximum energy consumption budget, speed and acceleration. In addition, the closed-form of outage probability is derived under the hybrid Line-of-Sight (LoS) and Non-Line-of-Sight (NLoS) probability channel model.

(2) The solution with long-term proactive optimization algorithm. The long-term proactive optimization mechanism is developed by leveraging the fact that if we know the start and the end positions of the mobile ground source,we can proactively infer or predict its mobile trajectory via GPS or BeiDou navigation systems. Then, a proactive optimization algorithm is designed accordingly for obtaining the long-term parameters of a flying UAV and a source node via carefully tailoring Primal-Dual Subgradient (PDS) method, Successive Convex Approximation(SCA)and Alternating Descent Method(ADM). In particular, we first obtain an approximation of original problem by applying the first-order Taylor expansion.Then,two sub-optimizations are formulated:one is the transmission power optimization with given UAV trajectory and the other is the trajectory optimization with given transmission power. Further, two subproblems are tackled via tailoring PDS method and SCA, respectively. To this end, a joint optimization algorithm is proposed by alternately solving the transmission power optimization and the trajectory optimization.

(3) Simulation results. Simulation results demonstrate the performance of the proposed algorithm under various parameter configurations. In addition, the UAV’s 3D trajectory and speed are also compared under different LoS probabilities, energy budgets and algorithms,respectively.

The reminder of this paper is organized as follows.The system model and problem formulation are presented in Section 2.An approximation of original problem is given in Section 3.The proactive mechanism and three algorithms are proposed in Section 4. Simulation results are provided in Section 5, followed by the conclusion in Section 6.

2. System model and problem formulation

2.1. System model

As shown in Fig. 1, there are two nodes, a Source Node (SN)and a Destination Node(DN),which distribute on the ground.They are suffering too weakly or even negligibly direct communication due to the severe obstructions, such as tall buildings or rolling terrain. SN is moving toward DN, during this period,in order to enhance the connectivity and real-time communication between SN and DN,a UAV is dispatched as a flying DF relay.

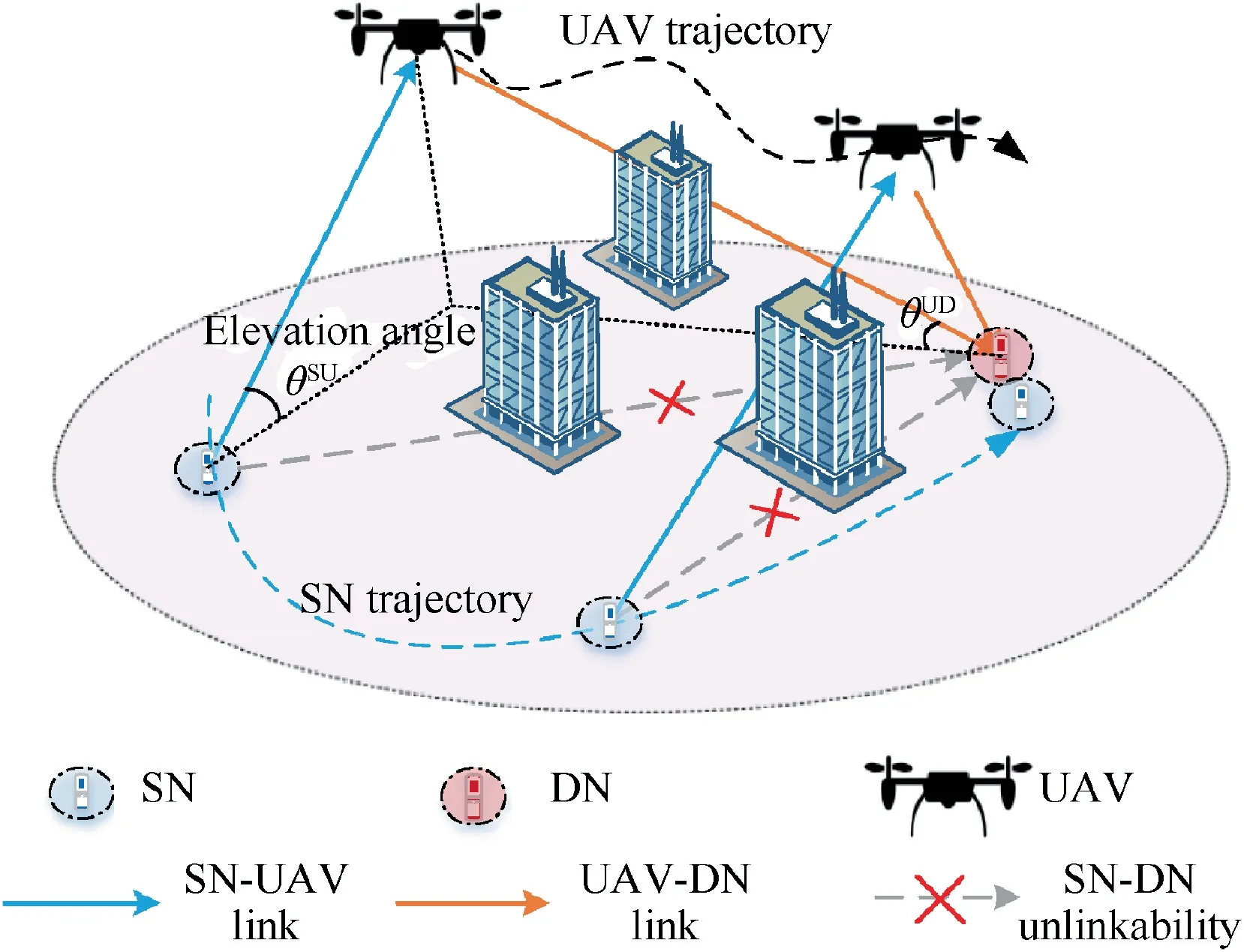
Fig. 1 Illustration of a UAV-assisted relay communication scenario with mobile ground user.

2.2. UAV-ground channel model

In this paper, the UAV is equipped with two antennas, one is the transmission antenna and the other is receiving antenna,which can transmit and receive data simultaneously.27In this paper, we consider that the UAV relay works in Frequency Division Duplex (FDD) mode, one of the half-duplex mode,allocating the same bandwidth to receive information from the SN and transmit it to the DN.10Therefore, there does not exist self-interference between UAV’s two antennas.

At the n - th time slot, the distance between UAV and SN,and that between UAV and DN can be respectively denoted as

The LoS and NLoS probability are affected by high buildings,tall trees and mountains,which exist in urban areas,suburban areas and rural areas,respectively.Therefore,the hybrid

The outage probability for communication can be defined as the probability that the SNR is lower than a predetermined threshold. Therefore, the outage probability between SN and UAV and that between UAV and DN can be respectively expressed as

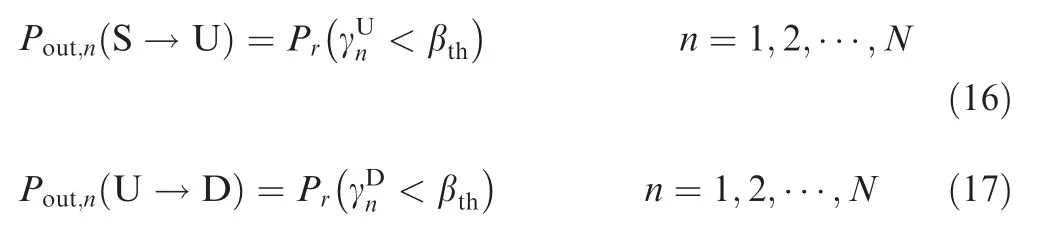
where βthis the predetermined SNR threshold value.

It can be observed that a complete and successful transmission needs that two stages, SN to UAV and UAV to DN, are both successful. Thus, the outage probability between SN and DN at the n - th time slot can be denoted as

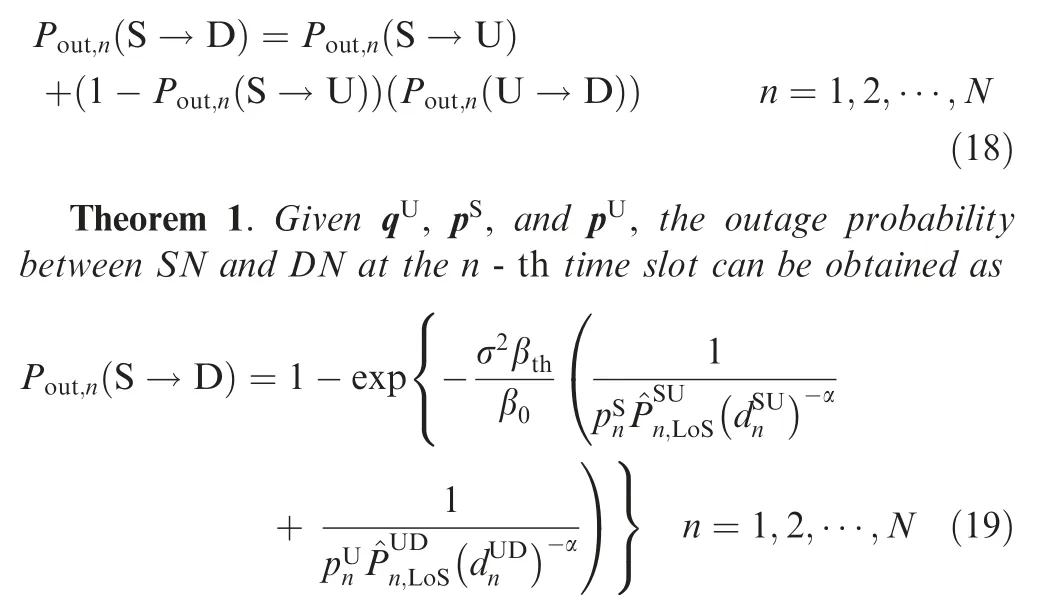
Proof. See Appendix A for the derivation details.

2.3. UAV energy consumption model

Energy consumption has an effect on the performance of UAV system and there are several studies considering UAV energy consumption. For example, the authors in Ref.15considered the limitation in energy consumption at both the Machine-Type Communication Devices (MTCDs) and the UAV station.Then,they investigated a UAV trajectory design problem from an energy efficiency perspective. In Ref.16, the authors investigated a completion time minimization problem in a UAV-assisted data dissemination system, while considering maximum energy budget, speed, transmit power of the UAV,and data requirement for each IoT device. The energy consumption generally includes communication-related and aerodynamic energy consumption. The UAV applied in this paper is a rotor-wing UAV, which can hover in the air with lower speed. Since we consider a 3D trajectory of UAV, the aerodynamic power of rotor-wing UAV at the n - th time slot can be modeled as37

where P0is the static power consumed for hovering.

Note that Etotalis the function of the UAV velocity/trajectory, and as a result, the velocity/trajectory of UAV may be different for different energy budgets.

2.4. Problem formulation for average outage probability minimization

Based on the above models, we formulate the average outage probability minimization problem in UAV-assisted relay system, which can be optimized by properly setting up UAV’s 3D trajectory qU, UAV’s transmission power pUand SN’s transmission power pS. Specifically, it can be expressed as

3. Approximation for LoS probability and problem reformulation

3.1. Approximation for LoS probability

3.2. Problem reformulation

4. Proactive optimization solution to problem P（3）

4.1. A long-term proactive optimization mechanism

Intuitively, one can design a reactive optimization mechanism as shown in Fig. 2 (a), in which one step includes two parts:given the current and the next positions of the mobile SN in advance, the short-sighted parameters of the UAV are optimized via optimization algorithms, gradually. To complete the whole mission, it needs to optimize the short-sighted parameters of the UAV in step-by-step or point-by-point manner until the source node achieves its end position. However,by leveraging the fact that if we know the start and the end positions of the mobile SN in advance,we can proactively infer or predict its mobile trajectory via GPS39or BeiDou navigation systems.40Then,according to the future mobile trajectory,a proactive optimization mechanism can be designed to obtain the long-term parameters of the UAV, as shown in Fig. 2 (b).The ‘‘short-sighted” denotes that one optimization only considers one time slot, which means that input one location of the SN and DN and then output UAV’s one position after one optimization.The‘‘long-term”denotes that one optimization considers the period of a task from start to finish, which means that input all locations of the SN and DN and then output UAV’s trajectory after one optimization. In addition, the reactive one cannot optimize the transmission power since it is point-by-point. In summary, the reactive one may be more real-time but is short-sighted and cannot optimize the transmission power. On the contrary, the latter tends to make a long-term consideration but is an off-line algorithm generally.In addition, to show the performance of the two mechanisms,we will compare them in the simulation.

According to the developed long-term proactive optimization mechanism, in this section, we propose a proactive optimization solution to problem P（3）. Firstly, P（3） is divided into two subproblems P（3.1） and P（3.2）, named the transmission power optimization and the trajectory optimization,respectively. P（3.1） is solved by leveraging Karush-Kuhn-Tucker (KKT) conditions and PDS method. P（3.2） is dealt with by SCA method. Next, we propose an efficient iterative algorithm to solve P（3） via carrying out the transmission power optimization P（3.1） and the trajectory optimization P（3.2） alternately.

4.2. Transmission power optimization with given UAV’s trajectory

where μk=γk/‖Tk‖2is step length, and γk>0.

In a nutshell, the method is summarized as Algorithm 1,namely, PDS-based transmission power optimization algorithm for P（3.1）.

4.3. Trajectory optimization with given transmission power allocation

Algorithm 1. PDS-based transmission power optimization for P（3.1）.1. Initialize the UAV trajectory qU-, the transmission power allocation pS，pU ｛ ｝（0）, the average outage probability θ（0）,Lagrange multipliers λ（0）i ， i=1，2，3，4，5, the tolerance of accuracy ψ>0 and l=0.2. Transform the primal problem P（3.1） into its corresponding Lagrange function and obtain the KKT constraints.3. Repeat.4. l=l+1.5. Update the Lagrange multipliers λ（l）i ， i=1，2，3，4，5, and｛ ｝（l） according to Eq. (32).6. Calculate average outage probability θ（l） according to the objective function of P（3.1）.7. Until primal variables pS，pU θ（l）-θ（l-1）θ（l-1） ≤ψ.8. Output the transmission power allocation pS，pU ｛ ｝（l） and average outage probability θ（l）.

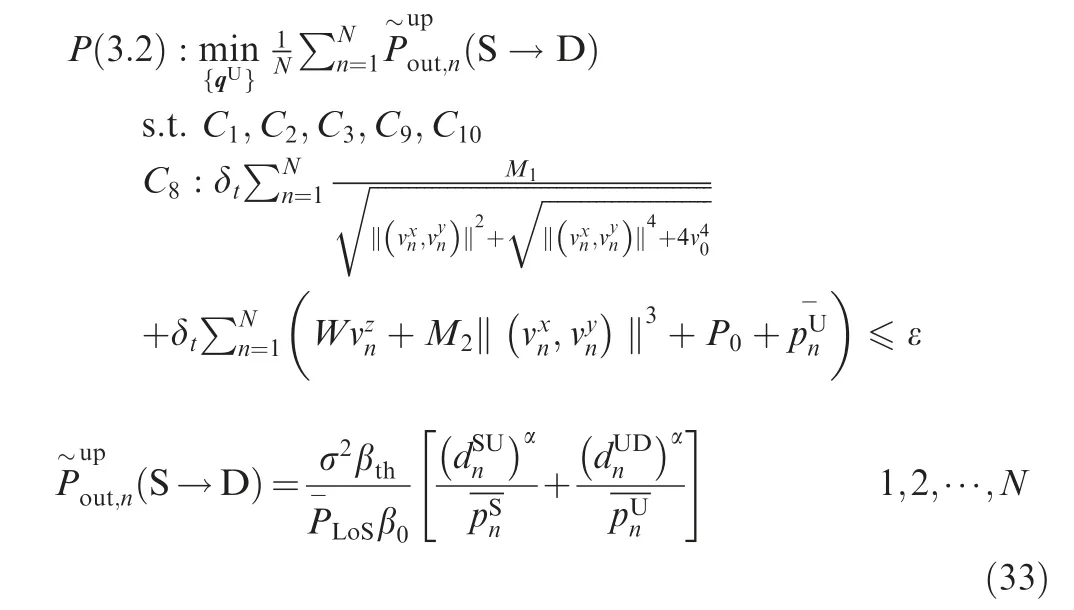
It can be observed that P（3.2） is a non-convex problem because C8is non-convex. In the following, we introduce the auxiliary variable ｛Bn｝ in P（3.2）. Then, we can have the following Theorem:

Theorem 1.

By introducing the auxiliary variable ｛Bn｝, P（3.2） can be approximately solved by dealing with the optimization problem P（3.2.1）:

By leveraging elementary operation, Eq. (34) is equivalent to

As a result, C8is transformed into C8.1.1, C8.2.1and C8.3.Therefore, problem P（3.2） can be approximately solved by tackling problem P（3.2.1）. This completes the proof.

Remark 2.Note that P（3.2.1）is a convex problem due to its objective function and constraints are convex. Thus, it can be directly solved by convex optimization tools, such as CVX.42The method is summarized in Algorithm 2, namely, SCAbased trajectory optimization for P（3.2）.

4.4. Joint trajectory and transmission power optimization

Algorithm 2. SCA-based trajectory optimization fo&r P（3.2'）.?

Based on the transmission power optimization and the trajectory optimization, we can obtain the solution to P（3） via solving P（3.1） and P（3.2） alternately. Since the solution to P（3） is the tight upper bound of P（1）, P（1） can be approximately solved by solving P（3）. Therefore, the solution to P（1） can be obtained via solving P（3.1） and P（3.2）alternately. The method is summarized in Algorithm 3,namely, joint optimization algorithm of trajectory and transmission power for P（3）.

Algorithm 3. Joint optimization algorithm of trajectory and transmission power for P（3）.1. Initialize the transmission power allocation pU，pS ｛ ｝（0）, the UAV trajectory qU ｛ ｝（0）, the tolerance of accuracy ψ>0 and l=0.2. Calculate θ（0） based on the objective function of P（3） with qU，pU，pS ｛ ｝（0）.3. Repeat.4. l=l+1.5. Fix qU ｛ ｝（l-1） and obtain average outage probability and transmission power allocation θ，pU，pS ｛ ｝（l） via solving P（3.1）.6. Fix pU，pS ｛ ｝（l）,and obtain average outage probability and trajectory θ，qU ｛ ｝（l） via solving P（3.2.1）.7. Until θ（l）-θ（l-1）θ（l-1） ≤ψ.8. Output the UAV 3D trajectory qU ｛ ｝（l） , the transmission power allocation pU，pS ｛ ｝（l） and the average outage probability θ｛ ｝（l）.

4.5. Complexity analysis

5. Simulation results and discussion

5.1. Simulation setup

In this section, we provide simulation results to evaluate the effectiveness of the proposed algorithms. Without additional specification, we consider an area with the size of 1 km×1 km×0.5 km, where a UAV serving as a mobile relay flies in a 3D space. The number of time slots is N=690. The source node is moving according to the preset trajectory, which is composed of three straight lines with uniform speed. Some key parameters are listed in Table 1 (One can refer to Refs.23,37,44,45for details). Moreover, the channel model related parameters a0=0.2, b=10, c=0.6,14α（0）=3.5 and α（π/2）=2.36In the following simulations,the UAV follows the SN (The difference is that the UAV has higher altitudes), which is used as a benchmark scheme,in order to verify the superiority of the proposed algorithms.In addition, the reactive optimization algorithm (renamed as Reactive opt.) is also compared with our proposed algorithms(Note that the Reactive opt. can only optimize UAV’s trajectory and tends to transmit data with the maximum transmission power optimization in one optimization since it is stepby-step or point-by-point. Therefore, considering the total transmission power constraints, the average transmission power is used as the UAV’s and SN’s transmission power ateach time in the Reactive opt.). To facilitate the readers, the proposed three algorithms in this paper are concisely and sequentially renamed as PDS-transmission power opt., SCAtrajectory opt., as well as JO-trajectory and transmission power, respectively.

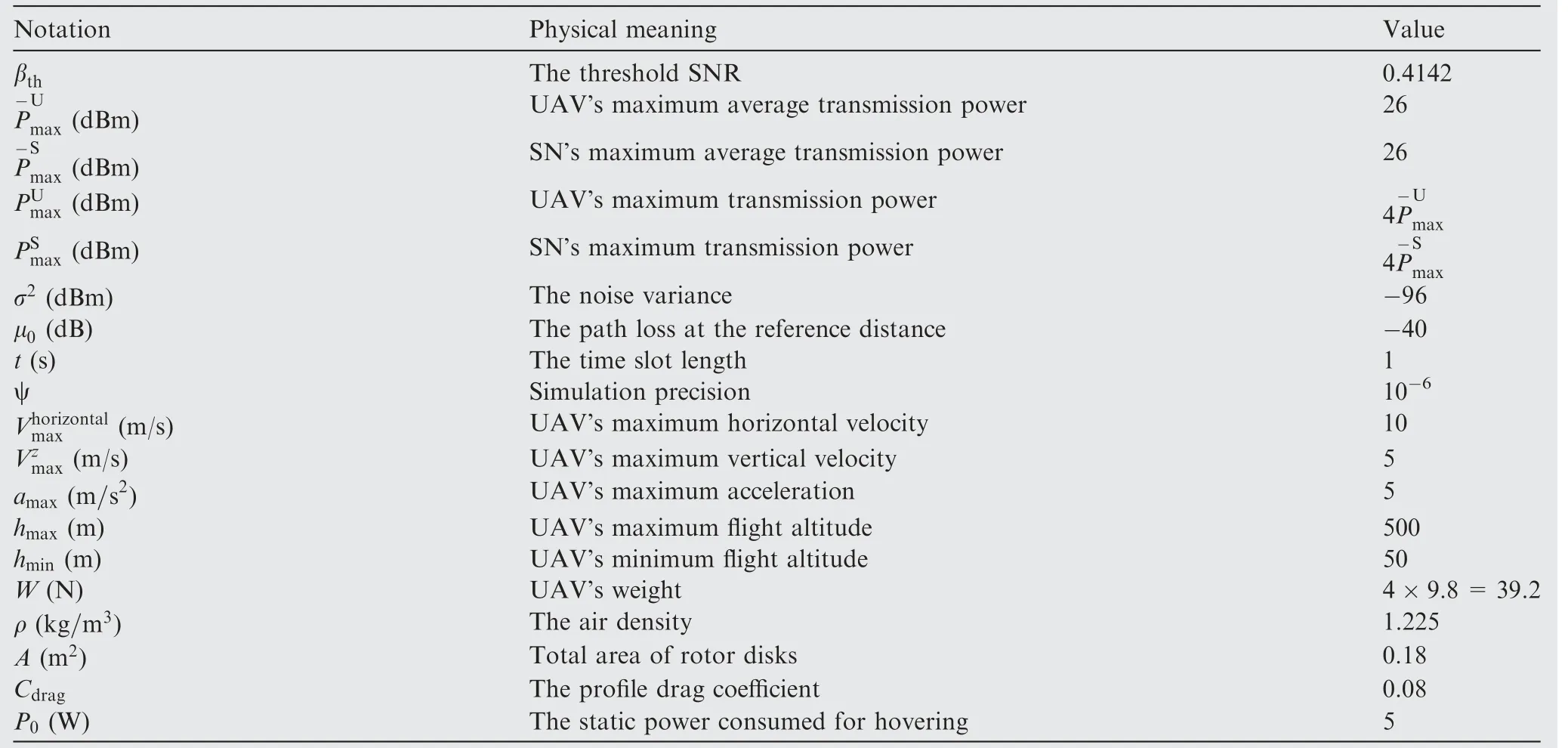
Table 1 Key simulation parameters.

5.2. Convergence verification

To verify the convergence of the proposed algorithms,we give the average outage probability iterative curves for JOtrajectory and transmission power with ζLoS=0.8 and ε=2.5×105J. It can be verified that PDS-transmission power opt. and SCA-trajectory opt. are both convergent as long as JO-trajectory and transmission power is convergent.In Fig. 3, the blue curve ‘‘JO-trajectory and transmission power” corresponds to the upper bound of average outage probability.The black curve‘‘Exact”denotes the exactly average outage probability, which is calculated by Eq. (26). It can be observed that the gaps between two curves are small,which can verify that the practical error is tight.In Fig.3,the average outage probability converges in a few iterations,which demonstrates the effectiveness of the proposed algorithms.

Fig. 4 compares the average outage probabilities of five algorithms under three different settings of LoS probability.The energy budget ε=4×105J.Note that the average outage probability is calculated without considering the first time slot since it cannot be optimized and its value will affect the other values. On the whole, as the LoS probability increases,the performance of average outage probability becomes better.In particular,in all cases,the average outage probability of the proposed JO-trajectory and transmission power algorithm is the lowest, Reactive opt. is the second, SCA-trajectory opt.is the third, PDS-transmission power opt. is the fourth, and Benchmark scheme is the highest. As is expected, JOtrajectory and transmission power has the best performance since it jointly optimizes the trajectory of UAV and transmission power of the source node and UAV. By contrast, SCAtrajectory opt. and PDS-transmission power opt. only optimize the trajectory of UAV or transmission power of the source node and UAV, respectively. In addition, the Reactive opt.has better performance in average outage probability since it can adjust its next position more freely,but it fails to achieve to the final position since it does not consider the end position constraint. In addition, compared with JO-trajectory and transmission power, the Reactive opt. has higher average outage probability since it cannot optimize transmission power allocation.

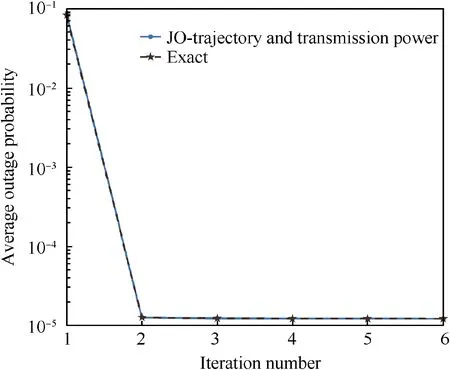
Fig. 3 Convergence of JO-trajectory and transmission power algorithm about average outage probability.

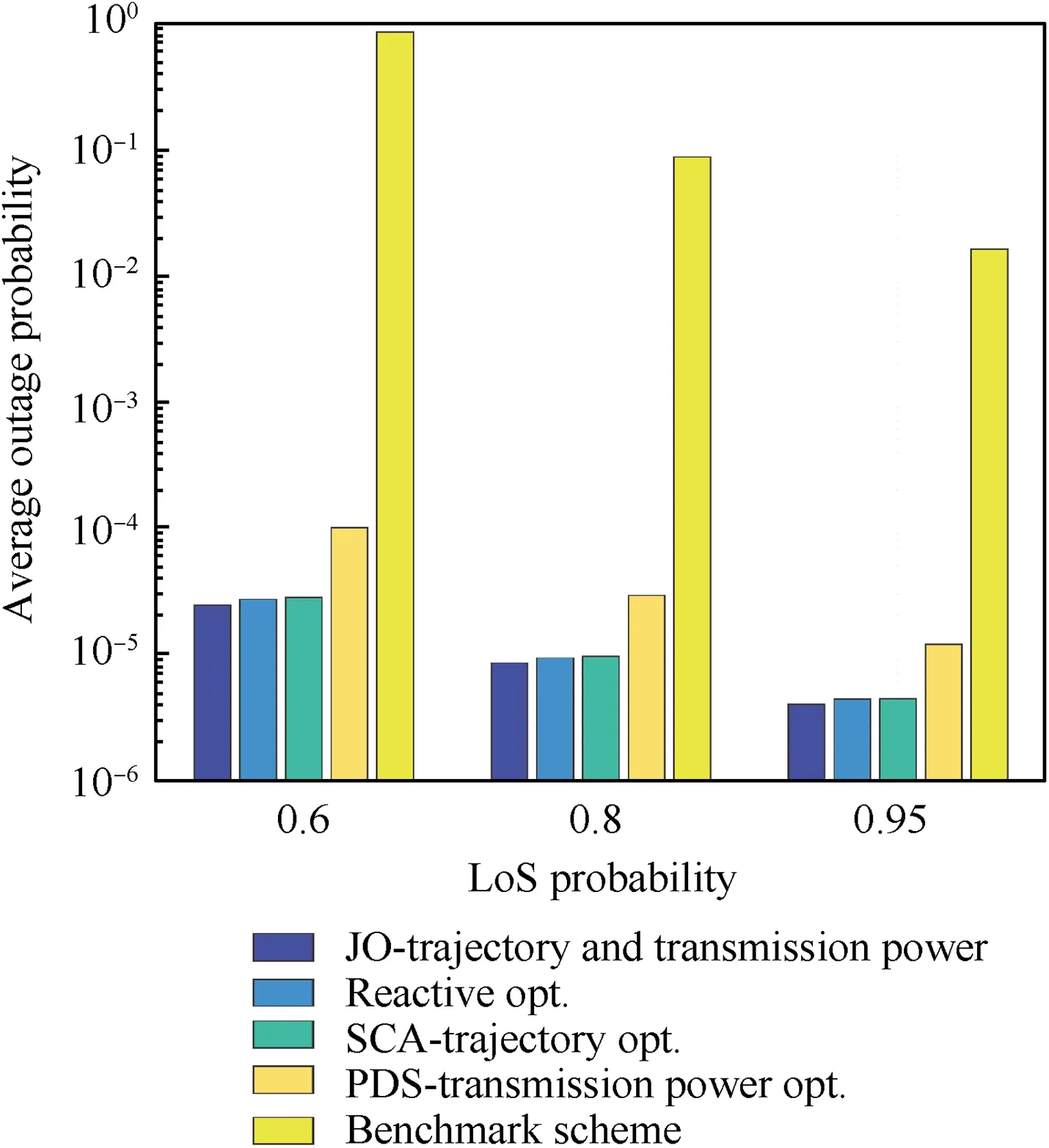
Fig. 4 Average outage probabilities of five algorithms under three different settings of LoS probability, which are 0.6, 0.8, and 0.95, respectively.

Fig. 4 compares the average outage probabilities of five algorithms under three different settings of LoS probability.The energy budget ε=4×105J.Note that the average outage probability is calculated without considering the first time slot since it cannot be optimized and its value will affect the other values. On the whole, as the LoS probability increases,the performance of average outage probability becomes better.In particular,in all cases,the average outage probability of the proposed JO-trajectory and transmission power algorithm is the lowest, Reactive opt. is the second, SCA-trajectory opt.is the third, PDS-transmission power opt. is the fourth, and Benchmark scheme is the highest. As is expected, JOtrajectory and transmission power has the best performance since it jointly optimizes the trajectory of UAV and transmission power of the source node and UAV. By contrast, SCAtrajectory opt. and PDS-transmission power opt. only optimize the trajectory of UAV or transmission power of the source node and UAV, respectively. In addition, the Reactive opt.has better performance in average outage probability since it can adjust its next position more freely,but it fails to achieve to the final position since it does not consider the end position constraint. In addition, compared with JO-trajectory and transmission power, the Reactive opt. has higher average outage probability since it cannot optimize transmission power allocation.

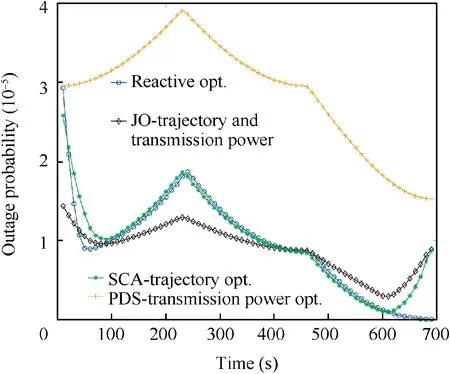
Fig. 5 Outage probabilities over time of four algorithms.

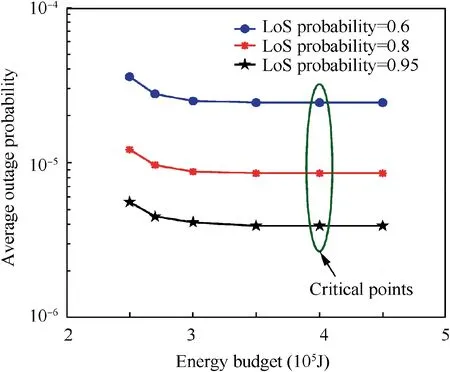
Fig. 6 Average outage probability vs. energy budget.

To further verify the effectiveness of the proposed algorithms,Fig.5 compares the outage probabilities over time of four algorithms with ζLoS=0.8 and ε=4×105J.To show the difference of the algorithms clearly, the benchmark scheme is not compared with the other four algorithms since the outage probability of benchmark scheme is very high obviously. It can be observed that PDS-transmission power opt. always has the highest outage probabilities, and the other algorithms have similar outage probabilities. Meticulously, the outage probabilities of JO-trajectory and transmission power are lower than the ones of SCA-trajectory opt. and Reactive opt.in most of time and higher than them after 460 s. It is expected that transmission optimization can optimize the transmission power to balance the outage probabilities and then reduce the average outage probability. After 600 s, the outage probabilities of JO-trajectory and transmission power and SCA-trajectory opt.are higher than the ones of Reactive opt.since the latter does not need to consider the end position constraint.

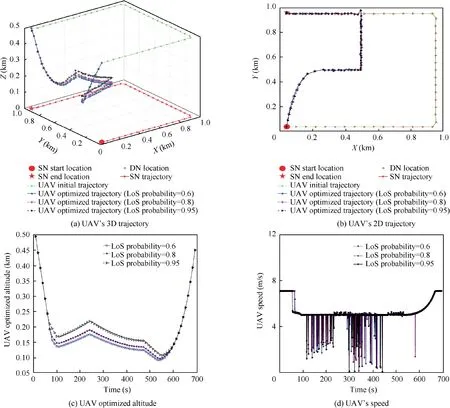
Fig. 7 UAV’s 3D trajectory and speed under three LoS probability settings, which are 0.6, 0.8, and 0.95, respectively.

5.3. Average outage probability - energy budget tradeoff

To show the relationship between average outage probability and energy budget, the average outage probabilities of JOtrajectory and transmission power algorithm under different energy budgets are given in Fig. 6. In addition, different LoS probability settings are also considered. On the whole, the higher the LoS probability is, the lower the average outage probability is, which is the same as Fig. 3. Analyzing each curve separately, it can be observed that the average outage probability decreases as the energy budget increases, until a critical point.This critical point means that the average outage probability has achieved the bottom and even if the energy budget goes up, it does not go down.

5.4.UAV’s 3D trajectory and speed under three LoS probability settings

In this subsection, we give UAV’s 3D trajectory and speed of JO-trajectory and transmission power algorithm under three LoS probability settings in Fig. 7, which are 0.6, 0.8, and 0.95,respectively.The red circle represents SN’s start location,the red five-pointed star denotes SN’s end location, and the rhombus represents DN’s location. In Fig. 7 (a), the UAV’s 3D trajectory is showed integrally. To discuss the details of UAV trajectory, Fig. 7 (b) and (c) show UAV’s 2D trajectory and altitude, respectively. The energy budget ε=3×105J.As shown in Fig. 7 (a) and (b), UAV tends to get close to the middle position, which is with ‘‘good communication condition”. The ‘‘good communication condition” means that both the SU link and UD link are with good performance. As shown in Fig.7(c),the UAV’s altitude which varies with time can be divided into three stages: ‘‘reduce”, ‘‘keep within an altitude range” and ‘‘increase”. In the ‘‘reduce” stage, UAV reduces its altitude to reduce the distances with SN and DN.However,to achieve the LoS probability threshold,its altitude is not infinitely low but keeps within an altitude range. In the‘‘increase”stage,UAV increases its altitude to achieve the end location.

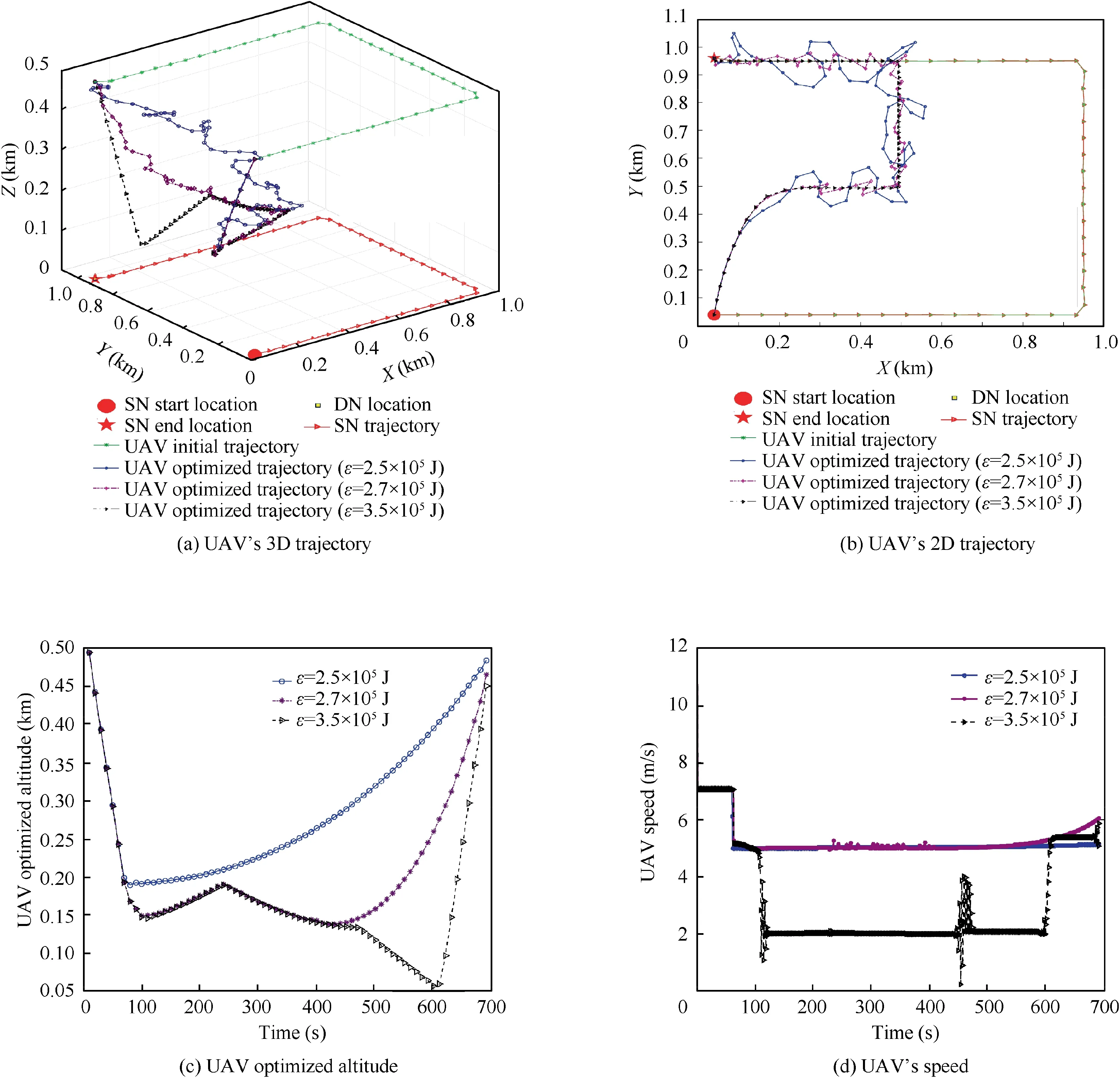
Fig. 8 UAV’s 3D trajectory and speed under three energy budget settings, which are ε=2.5×105, 2.7×105, 3.5×105 J,respectively.

In Fig.7(d),the UAV’s speed has the same phenomenon as the UAV’s altitude.In addition,it can be observed that UAV’s altitude increases as the LoS probability increases; however,UAV’s 2D trajectories and speeds are similar with different LoS probabilities. In summary, UAV tends to adjust its 3D trajectory to obtain the best channel conditions.

5.5. UAV’s 3D trajectory and speed under three energy budget settings

In this subsection, UAV’s 3D trajectory and speed of JOtrajectory and transmission power algorithm are given under three energy budget settings in Fig. 8, which are ε=2.5×105J, ε=2.7×105J and ε=3.5×105J,respectively. The LoS probability threshold ζLoS=0.8. Similar as Fig. 7, UAV tends to adjust its 3D trajectory to obtain the best channel conditions. Meanwhile, different energy budget settings also have different trajectories.In particular,when the energy budget is higher,the 2D trajectory is smoother and the UAV’s altitude and speed can change more freely, which are shown in Fig. 8 (b), (c) and (d), respectively. In summary,the UAV can achieve much better positions, which are with better channel condition when energy budget is higher. As a result, the average outage probability reduces as the energy budget increases until achieving a critical point.

5.6. UAV’s 3D trajectory and speed of two algorithms

Fig. 9 shows UAV’s 3D trajectory and speed of JO-trajectory and transmission power algorithm and Reactive opt. algorithm. ζLoS=0.8 and ε=5×105J. As we expect, there are some differences between them.In particular,UAV’s altitudes of Reactive opt. algorithm are lower than the one of JOtrajectory and transmission power algorithm in the beginning since the former always tends to choose the best position at every time slot. Accordingly, UAV’s speeds of Reactive opt.algorithm are higher than the ones of JO-trajectory and transmission power algorithm in the beginning.Then,the trajectory of them are similar until 600 s. After 600 s, to achieve the end position, the speed of the later increases; however, the former keeps it because it does not need to consider the end position constraint.

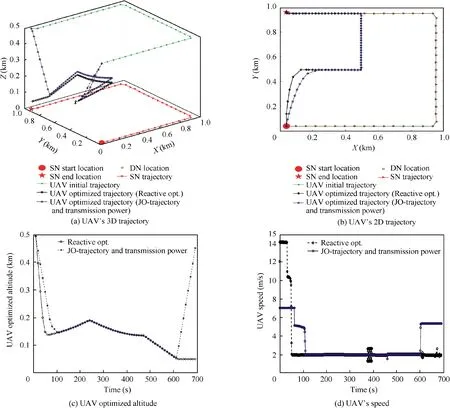
Fig.9 UAV’s 3D trajectory and speed of two algorithms,which are JO-trajectory and transmission power algorithm and Reactive opt.algorithm, respectively.

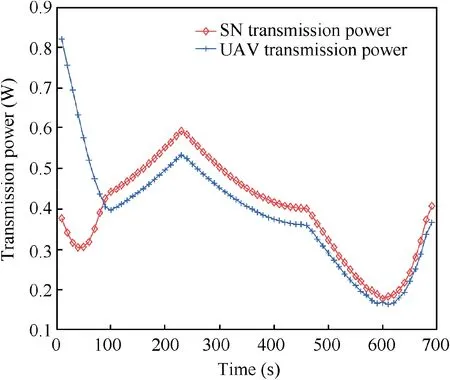
Fig. 10 Transmission power allocation over time.

5.7. Transmission power allocation

The transmission power allocation over time is shown in Fig.10.The LoS probability threshold ζLoS=0.8 and energy budget ε=3×105J. In the beginning, the UAV transmission power is higher than SN transmission power because the distance between SN and UAV is longer than that between UAV and DN. Then, the UAV transmission power is gradually reducing and lower than that of SN because the total transmission power is limited. In the final stage, both UAV and SN transmission powers increase as the link distances increase because the UAV gets close to its end location. In summary, it is expected that UAV and SN tend to transmit more power when the communication distance is long to balance the outage probability.

6. Conclusions

In this paper,we have formulated an average outage probability minimization problem for UAV-assisted relay system,while subjects to the constraints on the transmission power of the source node, the maximum energy consumption budget, the transmission power and the speed of the flying UAV relay.To solve this problem, we have derived the outage probability expressions, under the hybrid line-of-sight and non-line-ofsight probability channel model. Then, we have developed a long-term proactive optimization mechanism, which can obtain the long-term parameter settings of a flying UAV and a source node in a single step, based on which, we have proposed a proactive optimization algorithm via jointly optimizing the 3D trajectory of UAV and transmission power of UAV and source node.Simulation results demonstrate the performance of the proposed algorithm under various parameter configurations.

Note that there may exist some Co-Channel Interferences(CCIs) between multiple users, it is an interesting idea to consider the effect of CCIs on outage probability and we will do some explorations in future work.22,46In addition, another interesting future work is to extend the proposed method to a more complex system with multiple flying UAV relays and multiple mobile ground users.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This study was co-supported by the Natural Science Foundation for Distinguished Young Scholars of Jiangsu Province(No. BK20190030), the National Natural Science Foundation of China(Nos.61871398 and 61931011),and the National Key R&D Program of China (No. 2018YFB1801103).

Appendix A. First of all, following Eq. (16), we have