Feedback control of boundary layer Tollmien-Schlichting waves using a simple model-based controller
Yong LI, Zhengwu CHEN
a School of Mechanical and Electrical Engineering, Wenzhou University, Wenzhou 325035, China
b Key Laboratory of Aerodynamic Noise Control, China Aerodynamic Research and Development Center, Mianyang 621000, China
KEYWORDS Boundary layer instability;Control system;Feedback control;PID controller;Tollmien-Schlichting waves
Abstract The attenuation of spatially evolving instability Tollmien-Schlichting (T-S)waves in the boundary layer of a flat plate with zero pressure gradients using an active feedback control scheme is theoretically and numerically investigated. The boundary layer is excited artificially by various perturbations to create a three-dimensional field of instability waves. Arrays of actuators and sensors are distributed locally at the wall surface and connected together via a feedback controller.The key elements of this feedback control are the determination of the dynamic model of the flat plate boundary layer between the actuators and the sensors,and the design of the model-based feedback controller. The dynamic model is established based on the linear stability calculation which simulates the three-dimensional input-output behaviour of the boundary layer. To simplify the control problem,an uncoupled control mode of the dynamic model is made to capture only those dynamics that have greatest influences on the input-output behaviour. A Proportional-Integral-Derivative(PID) controller, i.e. a lead-lag compensator, combining with a standard Smith predictor is designed based on the system stability criterion and the specifications using frequency-response methods. Good performance of the feedback control with the uncoupled control mode is demonstrated by the large reduction of the three-dimensional disturbances in the boundary layer. This simple feedback control is realistic and competitive in a practical implementation of T-S wave cancellation using a limited number of localised sensors and actuators.
1. Introduction
In a low-perturbation scenario, transition from a laminar boundary layer to a turbulent one generally occurs through the amplification of naturally excited instability waves called Tollmien-Schlichting (T-S) waves. The amplitudes of the T-S waves grow at an exponential rate and, when reaching amplitudes of order 1% of the free-stream velocity, nonlinear interactions start to occur, eventually leading to breakdown and transition to turbulence.1The resulting turbulent boundary layer has considerably larger skin friction than the laminar one. Delaying the laminar-turbulent transition and maintaining a laminar flow as long as possible can significantly improve the aerodynamic performances in many applications, such as airplanes and turbines.
It is well known that active control techniques, such as wave cancellation,2-4opposition control5and wall-motion control6etc., have been demonstrated to be effective and efficient in delaying the laminar-turbulent transition by interfering the T-S waves in the boundary layer. However, Joslin, et al.7showed that, with these active open-loop control schemes,destruction of instability waves is sensitive to the wave parameters. Belson et al.8also demonstrated that this kind of active control could be degraded by the white noise or uncertainties in the boundary layer.Therefore,in the last decade,the possibility of using active closed-loop(feedback)control for boundary layer wave suppression had been widely investigated. The idea dates back to the works by Joshi et al.9,Cortelezzi et al.10and Bewley and Liu,11who employed feedback control theory to the problem of linearized plane Poiseuille flows/channel flows. More details regarding the combination of fluid mechanics and control theory can be seen in Kim&Bewley.12Compared to an open-loop control, a feedback control can generally (A) increase the accuracy, driving the difference between desired and measured responses to zero, (B) reduce the sensitivity to changes in components, seeking zero error despite changes in the plant, and (C) attenuate the effects of external disturbances and increase speed of response and bandwidth.Due to the advantages of using feedback control,many researchers have built control scheme based on Linear Stability Theory (LST) and/or Direct Numerical Simulations (DNS),especially the efforts in reducing model dimensions for the purpose of control design. For example, Bagheri et al.13constructed a Reduced-Order Model (ROM) based on the linearized Navier-Stokes (N-S) equation and designed a feedback controller to suppress successfully the two-dimensional(2D) disturbances in a flat plate boundary layer. In the same manner, Semeraro et al.14applied a Linear Quadratic Gaussian (LQG) regulator based on a ROM to attenuate the three-dimensional(3D)wavepackets of streaks and T-S waves.Semeraro et al.15extended the linear control system to fully nonlinear simulations to verify the possibility of delaying the transition to turbulence promoted by growing localized perturbations of finite amplitudes.Ahuja&Rowley16developed various ROMs of the input-output dynamics of high-dimensional linear unstable systems and applied the procedure to control the 2D low Reynolds number flow past a flat plate at a large angle of attack.Ma et al.17found ROMs using a system identification procedure called Eigensystem Realization Algorithm(ERA) and demonstrated the good performance in control of disturbances interacting with the flow past an inclined flat plate.Belson et al.8built a controller based on ERA and analysed the effects of different types and positions of actuators and sensors on controllers’ performance and robustness in the linearized 2D Blasius boundary layer. Based on DNS and plasma technology, Dadfar et al.18,19constructed an output feedback controller to successfully attenuate the T-S waves inside the boundary layer developing on both a flat plate and an unswept wing. Except the application on wall-bounded flows, similar feedback control scheme was also employed to control the oscillations of cavity flows.20-22
The numerical modelling feedback control approach has shown a significant reduction level of the disturbances (see the review by Bagheri&Henningson23).However,experimental application of these control algorithms has not yet been widely applied hitherto.The main challenges facing the experiments are: (A) how to design and build the feedback controller based on the complex and high-order transfer function of the boundary layer and (B) how to distribute locally and properly the sensors and actuators on the surface.Bewley24discussed the experimental feasibility of using Micro-Electro-Mechanical-Systems arrays of devices, but this seems only likely in the future as sensors and actuators become smaller and cheaper and vast numbers appear to be necessary.Semeraro et al.14constituted the first experimentally feasible simulation-based feedback control design using limited number of localized sensing and acting devices in a 3D setting.But the feedback controller requiring the actuators being connected with all the spanwise sensors (here called cross-linking)may make the feedback control difficult in a practical application. Nevertheless, the early experimental work using a feed forward control by Li and Gaster3showed that, without cross-linking,a row of simple controllers each connecting only the upstream sensor and the downstream actuator could sufficiently attenuate the 3D boundary layer disturbances.In a similar way, Lundell25experimentally investigated the reactive control of transition induced by free-stream turbulence and demonstrated the potential of four sensor-actuator pairs each working independently in reducing the growth of the amplitude of the streamwise velocity fluctuations. Fabbiane et al.26investigated the advantages and limitations of the closedloop system in control of 2D disturbances in experiments by applying an LQG controller and filtered-X least-meansquares controller and claimed that the adaptivity plays a crucial role in achieving robustness in transition control.
The objective of the work presented in this paper continues to investigate the experimental feasibility of using feedback control to reduce the perturbations in the boundary layer of a flat plate during the linear development stage. Our aim is to show that a simple and thus practical feedback control approach can produce worthwhile results in delaying laminar-turbulent transition in a practical application. Our focus is to find a simple and low-order linear dynamic model that is useful for feedback control and design a model-based controller that is feasible in an experimental application. The model itself may not be capable of capturing every aspect of the boundary layer flow dynamics, but rather on capturing those dynamics that have the greatest influences on the input-output behaviour.
The paper is organized as follows. In Section 2, we start with a description of the flow control set-up and numerical scheme used for T-S wave prediction. Section 3 can see the details of the feedback control algorithm based on the linear stability calculation of the T-S waves.The design of a feedback controller and its performance on reducing 3D disturbances are given in Section 4.Discussion and final remarks are drawn in Section 5 and Section 6, respectively.
2. Flow control set-up and numerical scheme for T-S waves
2.1. Control setup for T-S waves
We investigate the dynamics and feedback control of instability T-S waves developing in the boundary layer on a flat plate using numerical simulations. A 2D scheme of the feedback control to be modelled is shown in Fig.1 x0,x1,x2and x3represent the streamwise positions of an exciter, an actuator, a sensor‘‘A”and a reference sensor‘‘B”,respectively.An exciter at the streamwise position x=x0from the elliptic leading edge of the plate introduces small perturbations into the boundary layer to mimic the receptivity process of the naturally excited disturbances.By creating the upstream disturbances artificially there is a complete control of the wave field. The downstream linear developments of these disturbances(T-S waves)are measured by a sensor ‘‘A” at the position x2and another sensor‘‘B”at x3,respectively.Sensor A’s signal is fed back via a controller to an upstream actuator located at x1which generates control waves to interfere the existing T-S waves in the boundary layer.Sensor B’s signal is used to testify the feedback control performance.This feedback control set-up is similar to the one used by Li and Gaster3in their feedforward control except that the actuator here is positioned upstream the sensor.
The instability T-S waves are assumed to be produced by a shallow bump h(x)at one point on the boundary surface of the flat plate moving vertically with a periodic motion of frequency ω. The influence of the oscillating bump on the flow field can be found by a replacing the plane boundary by27Y(x,y)=h(x)e-jωt
This type of motion can be realized in an experiment by a loudspeaker (exciter) buried under a small hole which is flush-mounted on the boundary surface.3The actuator at x1performs the control action with the same type forcing as the exciter. In any experiment, the disturbances on the surface,such as skin-friction, can be detected by the sensors A and B using hot-films or wall surface-mounted hot wires gat the downstream positions.
2.2. Prediction methods for T-S waves
To design the feedback controller, we first need to find the dynamic model, i.e. the plant transfer function, of the boundary layer between the actuator and the sensor A in Fig.1.Theoretically,a boundary response measured by the sensor A at x2to an input-impulse introduced by the actuator at x1represents the plant transfer function. This transfer function generally varies with changing the streamwise separation (Δx21=x2-x1) between the actuator and the sensor A due to the connectivity of the disturbances from x1to x2. To establish this dynamic model,we first should seek solutions of the perturbation equations that satisfy the usual hydrodynamic boundary conditions of no normal velocity and/or non-slip flow on the boundary surface to find an impulse response of the boundary layer. The perturbation equations and the method of solution are summarized in the next Sections 2.2.1 and 2.2.2.For more details see the technical report by Gaster and Shaikh.27
2.2.1. Perturbation equations
The boundary perturbation amplitudes of interest are assumed to be small enough to allow the perturbation equations to be linearized throughout the flow field and the mean flow is parallel with no dependence on the streamwise position. With these two approximations introduced, the perturbation equations based on the linearized N-S equations can be separated in the space coordinates,enabling Fourier transforms in space to be taken. This generates the Orr-Sommerfield and Squire equations with all the perturbations in the directions of the x, y and z axes. For convenience, the equations are reconstructed into equations for three orthogonal perturbations u, v, w and three perturbation vorticity components ζx, ζy, ζz.We take space Fourier transforms denoted by the caret symbolin the streamwise x and spanwise z directions as

where Q represents all variables of perturbations and their derivatives, and α, β represent the streamwise and spanwise wavenumbers,respectively.By substituting the inverse Fourier transforms of Eq. (1) in to the linearized N-S equations, one can obtain the reduced two 1st-order and three 2nd-order perturbation equations as


Fig. 1 2D set-up scheme of feedback control of boundary layer T-S waves on a flat plate.

With the Fourier transform relation Eq. (1),Eq. (7) can be used to give necessary wall boundary conditions(η=0)in the variables used in the Eqs. (2)-(6). Far from the flat plate(η →∞) the boundary conditions that all the perturbations decay exponentially are imposed.
2.2.2. Method of solution and validation
The 6th-order set of linear ordinary differential Eqs. (2)-(6)with both boundary values (Eq. (7)) and far-field boundary conditions are solved by a shooting method that incorporates a simple way of eliminating the parasitic growth that arises with these stiff Reynolds number equations. The perturbation equations are integrated in a rectangular integration domain by a 4th-order Runge-Kutta method from the outer boundary conditions marching towards the wall boundary.There are six independent solutions,but because the far-field boundary condition requires all perturbations to decay, three arbitrary constants can immediately be equated to zero. The remaining three roots are evaluated by integration from the outer regions to the wall where the boundary value of(Eq.(7))is applied.At the end of each integration step all the solution variables and their derivatives are defined in any convenient way to provide new variables for the next integration step. This process of stepwise integration and filtering is continued to the wall where the remaining boundary condition is applied. An iteration scheme is setup to vary the wavenumbers or frequency parameter until all the velocity components become zero at the wall boundary.
In our current work, the perturbations are introduced at x=x0,the shallow bump function h(x)can be taken as a delta function.

which is substituted to Eq. (7) to give the necessary boundary conditions. For a piston-exciter well retracted below the plate surface or a loudspeaker-exciter buried, the boundary value has only v-component. The solution form with this pure vcomponent boundary values appear as
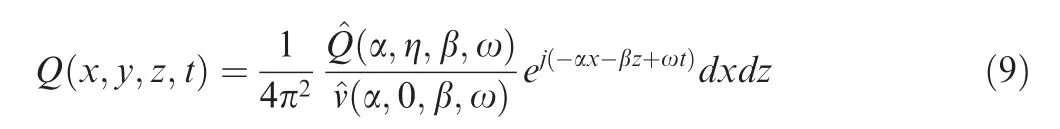
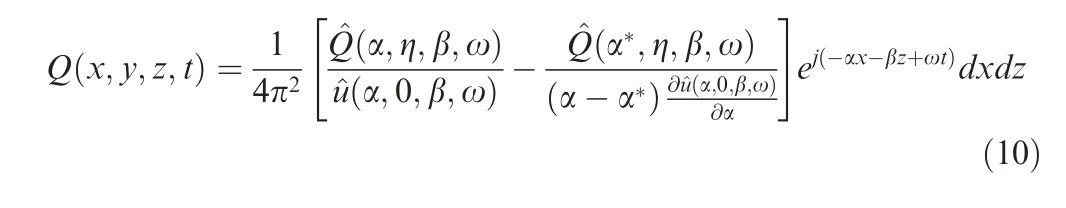
This numerical scheme is especially useful for feedback flow control design because it separates out the near-field features and the far field eigensolution which represents the development of the T-S waves in the boundary layer.
The streamwise×nd spanwise z directions are discretized at 1 mm intervals and in wall-normal y direction the nondimensional η=y[U0/(νx)]0.5is used. A physical resolution of 1 mm requires that the range of integration be set to cover--π×δ* to π×δ*, where δ* is the displacement thickness in millimetres. A total of 1024 streamwise wavenumbers α from-512 to 512 and 100 spanwise wavenumbers β are applied to accommodate a wide physical domain. For 2D cases,β is zero.For 3D cases,the formulation is virtually identical to the 2D situation for each spanwise wavenumber β and the result is then transformed in physical β-space.
Numerical simulation of the perturbations using computer codes based on the solution methods had already been compared with experiments by Gaster and Shaikh.27Fig. 2 shows their comparison of the in-phase u-components between the experiments and the calculations of a point source moving vertically with a periodic motion of frequency f=50 Hz. On the center x-y plane, close to the source (x ≤150 mm) the agreement is truly remarkable in the boundary layer. The comparison in the z-y plane just 20 mm downstream from the source also provides encouraging support of the numerical simulation. Far downstream, where the boundary layer in the experiments has grown while the calculation is made based on parallel flow, agreement is somewhat qualitative. Based on the similar numerical prediction, Li and Gaster3designed a feed forward control to suppress successfully the T-S waves in the boundary layer on a flat plate. In this paper, the dynamic model for the design of feedback control of T-S waves is determined also based on the same numerical scheme and computer codes.
3. Strategies for designing feedback control of T-S waves
3.1. Development of a wave-packet in boundary layer at Re=1000
In our study case, the uniform free stream velocity is set to U0=12 m/s and the exciter is positioned at x0=400 mm downstream from the elliptic leading edge.The Reynolds number Re (=U0δ*/ν) based on δ* at this exciter is 1000 for this flow condition. Before making a decision of the feedback control strategy,it is worthwhile knowing how the boundary layer responses to a unit impulse introduced by a point-source exciter on the center-line z=0 since the impulse response determines the plant transfer function of a control system.The form of the impulse response is a Gasterwave-packet28in the boundary layer. We assume that the development of the wave-packet is detected in an experiment by a series of hot-film distributed spanwisely and streamwisely on the plate surface, so the variable of the z-vorticity ζzon the surface is measured. Fig. 3 shows the development of the vorticity ζzwave-packet at four x-streamwise positions. The spanwise range is from z= -100 mm to 100 mm. For the short distances, i.e.Δx=20 mm and 40 mm, from the exciter source, the amplitudes of the wavepacket drop rapidly outside the center-line.In the case of Δx=20 mm shown in Fig. 3(a), the amplitude at z=2 mm is only 20% and 30% of the ones at z=0 mm and z=1 mm respectively, indicating 97% of the wavepacket energy is concentrated on the central area between z= -1 mm and z=1 mm. At the downstream distances of Δx=100 mm and 200 mm, the wavepacket energy spreads in the spanwise direction. In the case of Δx=200 mm shown in Fig. 3(d), the Gaster wavepacket is well developed and a part of energy spreads to the spanwise region outside of z=20 mm.
3.2. Flow feedback control strategy of using uncoupled mode
The development of the wavepackets shown in Fig. 3 can represent the impulse response of the boundary system between the actuator and the sensor A, provided that the same type of disturbances now is introduced into the boundary at x=x1. As far as the experimental application is concerned,the actuator is located in this paper at x1=500 mm, i.e 100 mm downstream from the exciter source, since the validation in Fig. 2 shows that this distance can give fairly accuracy prediction of the disturbances. Fig. 3 shows that at short distances from the source the energy is concentrated on the central area, so the 3D development of the impulse can be treated as 2D if the sensor A is very close to the actuator.To avoid the near-field effects of the actuator on the sensor A, two distances of Δx21(=x2-x1)=20 mm and 40 mm are considered, and then the plant transfer function can be found by setting the spanwise wave number β=0. If this control strategy produces a very encouraging results,it is not necessary to consider the 3D full transfer function which requires crosslinking of all the spanwisely distributed activating and sensing devices.3This uncoupled control mode would be very practical and competitive in a real experiment application.
According to the streamwise separation between the sensing and activating devices in Fig. 1, the flat plate boundary layer can be divided into four domains which are represented respectively by transfer function P02(s) between the exciter and the sensor A, P12(s) between the actuator and the sensor A,P13(s) between the actuator and the sensor B, and P03(s)between the exciter and the sensor B. These transfer functions indicate quantities given in the frequency-domain where s=jω.Based on this setup,Fig.4 depicts the whole block diagram of the boundary layer feedback control of T-S waves.For the controller-design purposes in this paper, the plant transfer function P12(s) between the actuator and the sensor A is of main concern. C(s) is the transfer function of the feedback controller.
The block diagram part enclosed by the dot-line in Fig.4(a)represents the feedback (closed-loop) control system which is expanded and clearly expressed in Fig.4(b).The control signal SC(s) is introduced into the boundary layer by the actuator at x1with the periodic jet-type forcing. The reference signal R(s)represents the desired signal that the output SA(s) of the feedback control system at x2is expected to track.N(s)is the external disturbance detected at x2which is introduced initially by the upstream exciter at x0, and is also the T-S waves that the feedback control is expected to interfere. The performance of the feedback control is judged by the far downstream sensor B’s signal SB(s).
The key element of this paper is to study the dynamic model, i.e. the open-loop plant transfer function P12(s), of the feedback control system between the actuator and the sensor A. Based on the block diagram in Fig. 4(b), the output SA(s) w.r.t. the reference R(s) and the external disturbance N(s) can be given by
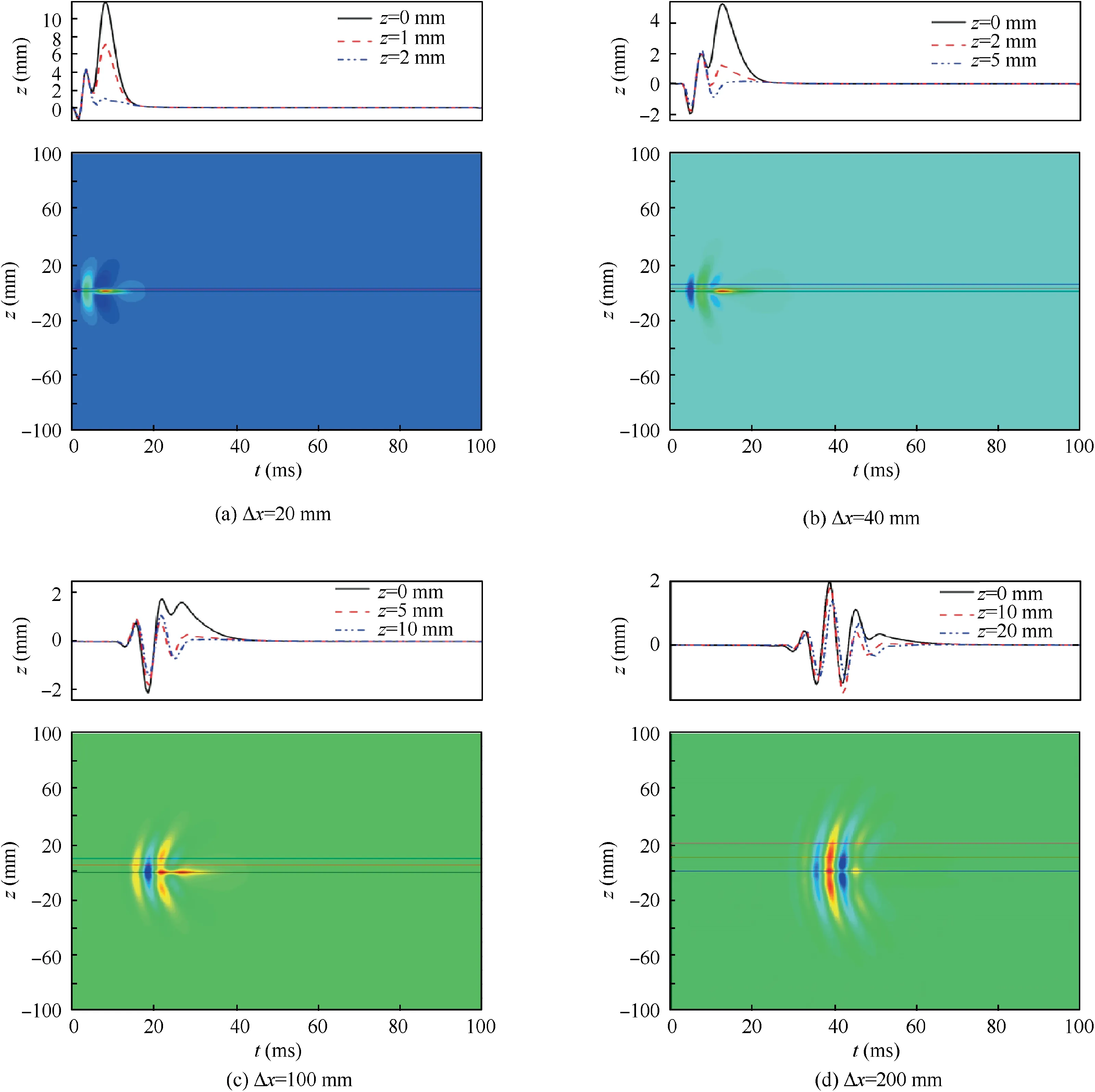
Fig. 3 Downstream development of a wavepacket in the boundary layer of a flat plate. The data are taken at 4 different streamwise distances from the exciter source located at x0=400 mm from the leading edge of the plate.

The external disturbance N(s)=E(s)P02(s), where E(s) is the exciter’s function.For the stabilization purpose of the control system,we only consider the closed-loop transfer function G(s) w.r.t. SA(s) and R(s), which is given by
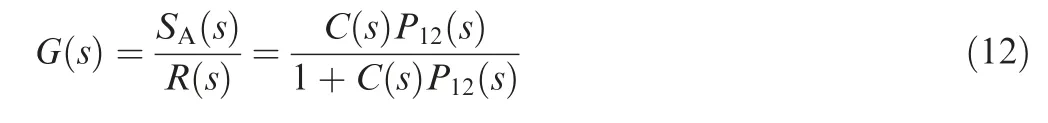
where the characteristic equation is 1+C(s)P12(s)=0 whose roots are the poles of the transfer function G(s).The actuators’signal SC(s) has the form of
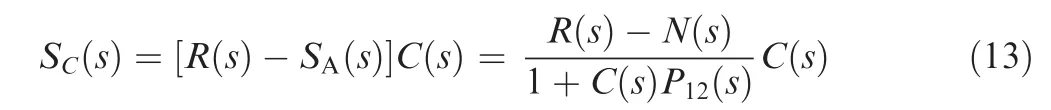
The performance of the feedback control scheme is testified by the sensor B’s signal which is given by

For flow control purposes,our aim is to eliminate the external disturbance N(s). Thus, we set the desired reference R(s)that the signal SA(s) should track to be zero, i.e. R(s)=0.To design the feedback controller C(s), the key element next is to find the plant transfer function P12(s) in frequencydomain,which can be determined from the frequency response of the boundary layer in the following section.
3.3. Plant transfer function P12(s)
We look at the way of determining the plant transfer function P12(s) of the boundary layer flow from the linear stability calculation described in Section 2.To obtain the transfer function P12(s), we suppose that a unit mass impulse is introduced by the actuator at x1. The signal measured at x2is the impulse response of the plant boundary layer and also the transfer function P12(s) in frequency-domain. Here, we use the surface skin friction related to the z-vorticity ζz(x,t) on the surface as the measured signal. It can be defined in Fourier space
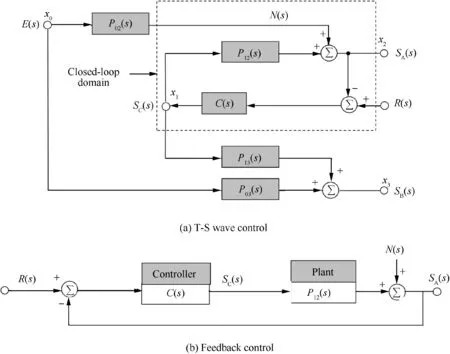
Fig.4 Block diagram of boundary layer feedback control of T-S waves on flat plate.The closed-loop domain enclosed by dot-line in(a)presents the feedback control system that is expanded in (b) for clarity. The capital letters indicate quantities given in frequency-domain where s=jω.
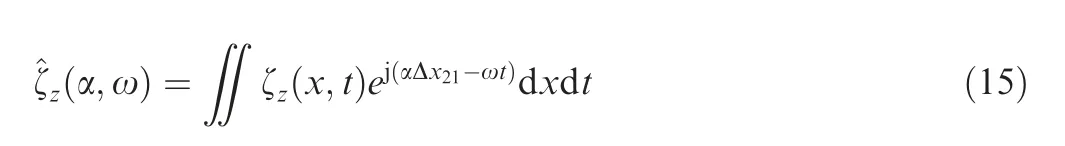
where the streamwise separation distance Δx21=x2-x1and the value(α,ω) includes both the unstable Eigen solutions and the near-field elements, arising from the continuous spectrum and the damped modes.Similarly,the skin friction acting on any positions in the boundary can be evaluated for any given source signal by a convolution of the input excitations and the impulse response at an appropriate streamwise separation distance.
Now it is time to determine the explicit expression of the dynamic model P12(s) which should describe the amplification of velocity and vorticity perturbations in the boundary layer as they travel downstream. One way to visualize how a system responds to an input is to use the frequency response of the system, especially when the transfer function of a system is unknown in theory. One advantage of using frequency response design,as mentioned by Franklin et al.29,is the ease with which experimental/numerical information can be used for design purposes. The output magnitude and phase of a plant boundary layer undergoing a sinusoidal input excitation are enough to design a suitable feedback control. Finding poles and zeros or determining system matrices (mostly applied for the design of boundary layer feedback control in literatures) is not necessary to arrive at the system model.Another advantage is that the design is the easiest method to use for designing compensation. A simple rule can be used to provide reasonable designs with a minimum of trial and error.
We first present Bode plot30in Fig. 5 by plotting a magnitude versus frequency and a phase versus frequency for different streamwise actuator-sensor separations Δx21, and then obtain the mathematical function P12(s) approximately from the Bode plot. This plot is obtained by using sinusoidal input excitation to the boundary layer in the frequency range from f=0 Hz to f=800 Hz at the frequency interval of 10 Hz.The frequency response shown in Fig. 5 is the behaviour of the boundary layer to the input driving disturbances.It is clear that each separation has a different frequency response, indicating different plant transfer functions. The magnitudes of the disturbances at the frequencies below ω=512 rads/s(f=80 Hz) and above ω=1256 rads/s (f=210 Hz) decay with increasing the separation distance. Therefore, only the magnitudes of frequencies between ω=512 and 1256 rads/s amplify for the current Re=1000 as the disturbances convect downstream.Fig.5(b)shows that in the frequency range interested, the phase angle is far less than-180°, indicating that the plant boundary layer is a time-delay system due to the convective nature of the disturbances between the actuator and the sensor A.
The transfer function P12(s)can be derived within some certain degree of accuracy by fitting an asymptotic magnitude plot(in dB)to the calculated data in Fig.5(a).Often the phase versus logarithmic frequency, as calculated from the approximate transfer function,will not completely agree with the corresponding curve, especially when the transfer function is irrational. Therefore, to match the data reasonably, both the magnitude and phase curves in Fig. 5 must be considered simultaneously. Since the high-frequency components decay rapidly as the streamwise separation Δx21increases, the asymptotic slopes of the curves increase quickly. Thus, the transfer function must be a higher-order function at a longer separation distance. To simplify control design and reduce the function order, we only choose two separations of Δx21=20 mm and 40 mm because at this short distance the transfer function based on the uncoupled mode may capture the development of an impulse in 3D modes, as shown in Fig. 3. Based on the amplified modes of the frequency range between ω=512 and 1256 rads/s we can finally determine respectively the approximate transfer function P12(s) from the Bode plots as
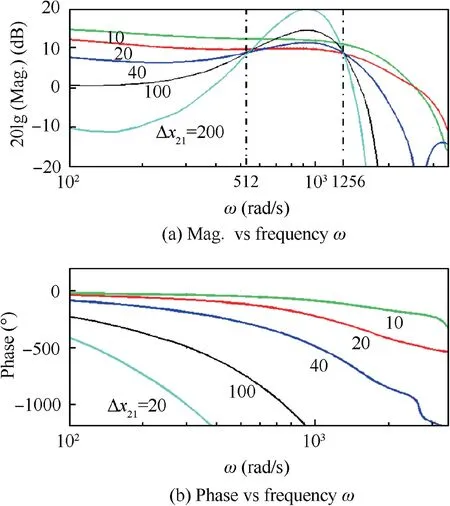
Fig. 5 Bode plot for boundary layer transfer functions P12(s) at different streamwise separation Δx21 between the actuator and the sensor A.
The transfer functions Eqs.(16)and(17)are 3rd-order and 5th-order respectively, and both are clearly irrational due to the time-delay τ in the term e-τs(τ:the time taken for a disturbance generated at the actuator to propagate to the downstream sensor A). The time-delay for distance Δx21=20 mm is τ=0.0024 s while it is τ=0.0078 s for Δx21=40 mm. It is clear that Eq. (16) has no positive pole in the Right-Half-Plane (RHP) while there are two positive poles in the RHP for Eq.(17).No zeros in both functions means that the system has no transmission-blocking property, i.e. being response to all frequencies.
We now verify the dynamic model P12(s) in the frequency domain by comparing their frequency responses and then in the time domain by comparing their transient impulse response. Fig. 6 shows the comparison of the transfer functions from the linear stability calculation to that given by the simplified models Eqs. (16) and (17). It can be seen that both the models capture the important dynamical features of the boundary layer: near unity gain at low frequencies; amplification of disturbances at mid-frequencies; attenuation of disturbances at high frequencies; and appropriate phase in the frequency range of ω=512-1256 rads/s that amplifies downstream. The impulse responses in time domain also show the reasonable accuracy of the transfer functions, especially for Eq. (16) which will be used to design the feedback controllers C(s) for the boundary layer T-S waves cancellation in Section 4.
4. Model-based feedback controller and its performance on T-S wave cancellation
4.1. Lead-lag compensator (PID) with Smith predictor
Another key element of this paper is to find numerically a feedback controller based on the simplified low-order model P12(s)denoted by Eq. (16) that can be practically applied on a flat plate to control the boundary layer instability T-S waves. All the numerical works including the design of the controller and the later control performances are carried out using MATLAB codes. The boundary layer system is irrational due to the time-delay which may decrease the system stability,deteriorate the dynamic performance and cause overshoot and vibration. A Smith predictor is well known as an effective delay-time compensator for a stable process with large delaytime.31,32. To reduce these time-delay effects, we first apply a standard Smith predictor in parallel with the controller in another feedback loop and the closed-loop domain in Fig. 4(b)is now changed to the one in Fig.7.With this Smith predictor, the feedback transfer function in Eq. (12) is changed to
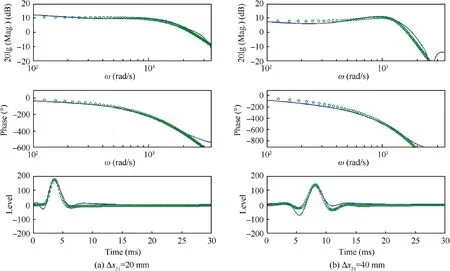
Fig.6 Frequency and impulse response of boundary layer transfer function P12(s):as calculated in linear stability simulations(denoted by -); and approximated functions of Eqs. (16) and (17), denoted by ‘°’.

Fig. 7 Block diagram of feedback control system with a Smith predictor which is enclosed by dotted-line.
where the characteristic equation is 1+C(s)P(s) = 0 which has no delay-time term and P(s) takes the form of
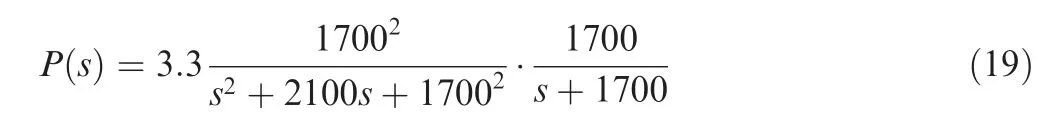
To simplify the control block with the Smith predictor, an equivalent block diagram to the one in Fig.7 is formed by setting the term eτsin the feedback loop,as shown in Fig.8.Now,the controller’s signal SC(s) (by setting the desired reference R=0) is

To control the boundary layer instability waves,we apply a lead-lag compensator as the controller, i.e. a PID controller,whose transfer function C(s) has the general form of29
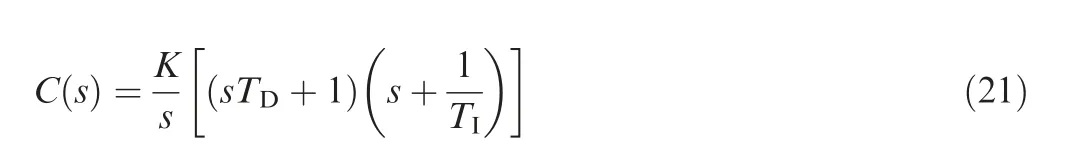
This controller is typically added to a plant system to improve the system’s stability and error characteristics because the process itself cannot be made to have acceptable characteristics with proportional (gain K) feedback alone. Generally,PD control with term sTD+1 adds phase lead at all frequency above the break points; and therefore, increases the crossover frequency and the speed of response. PI control with term s+1/TIincreases the frequency response magnitude at frequencies blow the break points, thereby, decreasing steady-state errors.The problem now is to find values for the three parameters of the controller transfer function K, TDand TIthat will satisfy the specifications and stability criterions.
4.2. Parameters of lead-lag compensator

Fig. 8 Equivalent block diagram of feedback control system after being compensated by a Smith predictor.
The easiest approach is to work first on the phase so that sufficient Phase Margin (PM, here we set the PM requirement of 45°) is achieved at a reasonably high frequency, which can be accomplished primarily by adjusting the parameter TDto be value of 1/2000 in this case. Then we select TIwhich is larger than TDto increase the gain at zero frequency, which reduces the steady-state errors.Our choice for TIis a factor of 2 larger than TD,which only slightly impact the phase at crossover frequency (ωc), i.e. lowering the PM by 2°. Once the phase is adjusted, we establish the crossover frequency ωcand then determine the final gain K=0.4 so that ωcis at the point corresponding to the required PM of 45°.With these values of the parameters, the equation of the lead-lag compensator is completed as
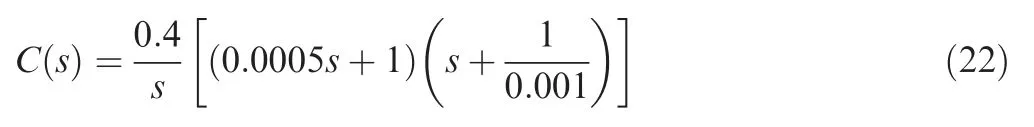
The comparison of the Bode plots for the uncompensated P(s) and compensated systems C(s)P(s) is shown in Fig. 9. The PM of the uncompensated system is approximately 5° at the crossover frequency of ωc=2400 rads/s while the compensated system has a PM of 45° at ωc=1930 rads/s. The gain of low frequency of the P(s) is also increased with the leadlag compensator.
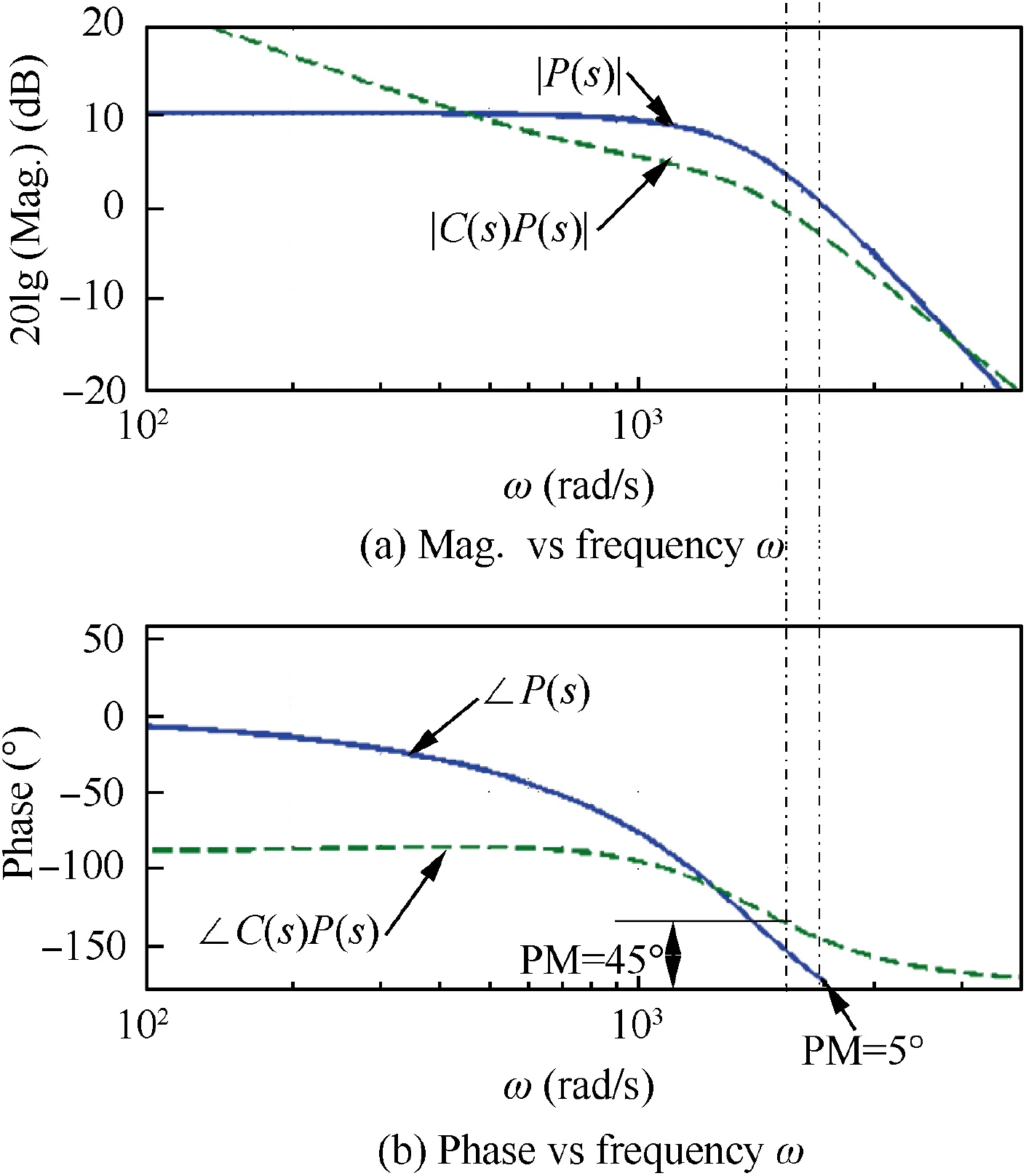
Fig. 9 Frequency response of lead-lag compensation design.
Nyquist stability criterion is used to determine the stability of the feedback control system in terms of the frequency response of the system open-loop transfer function. Fig. 10 shows the Nyquist plots33of the open-loop system P(s) and the open-loop compensated system C(s)P(s). For the system P(s) in Fig. 10(a), the Nyquist plot crosses the negative real axis at point (-0.72, 0). So, for the proportional gain K>0,there are two possibilities for the location of-1/K: inside the two loops of the Nyquist plot at large values Kl,or outside the Nyquist contour completely at small values Ks. Since the system P(s) has no roots in RHP, for the stability criterion,there should be no circulation of the-1/K, i.e.-1/Ks< -0.72. Therefore, for uncompensated system P(s), the proportional gain K must be less than 1.4(K<1.4),otherwise the feedback control system would be unstable. However, for the compensated system C(s)P(s)in Fig.10(b),we can see that the Nyquist plot crosses the origin point (0,0), indicating that there is no circulation of point-1/K for any positive value K.Thus,the feedback control system with the lead-lag compensation C(s)is stable for positive value K.Large value of K would benefit reducing the steady-state error but also decreasing the phase margin PM and damping of the system.Therefore,compromise is made in our control system design. The value of K=0.4 in our case is selected on the condition that K does not reduce the PM specification and we let the integration term(s+1/0.001) in C(s) reduce the steady-state errors.
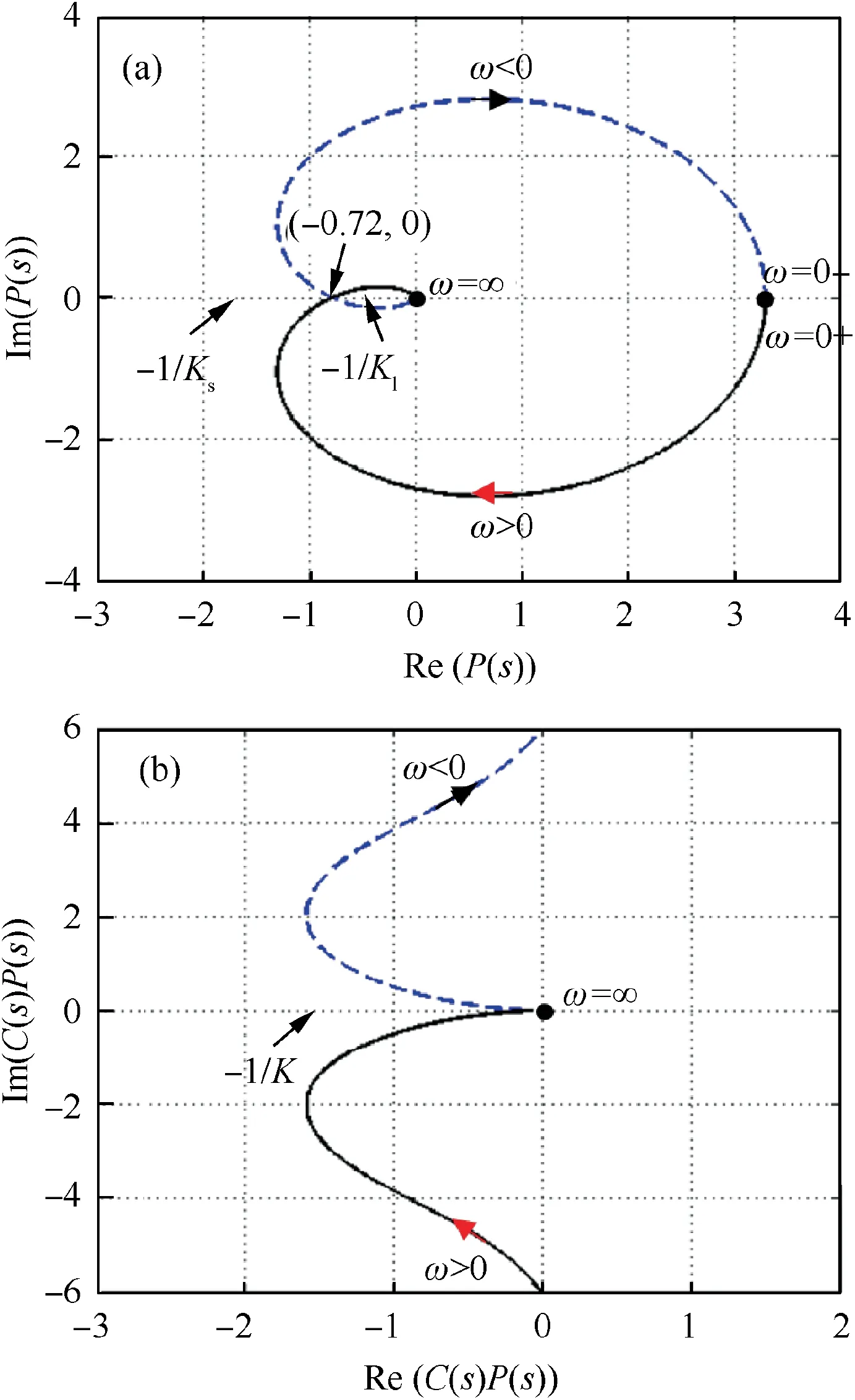
Fig. 10 Nyquist plots for (a) uncompensated open-loop system P(s) and (b) lead-lag compensated open-loop system C(s)P(s).
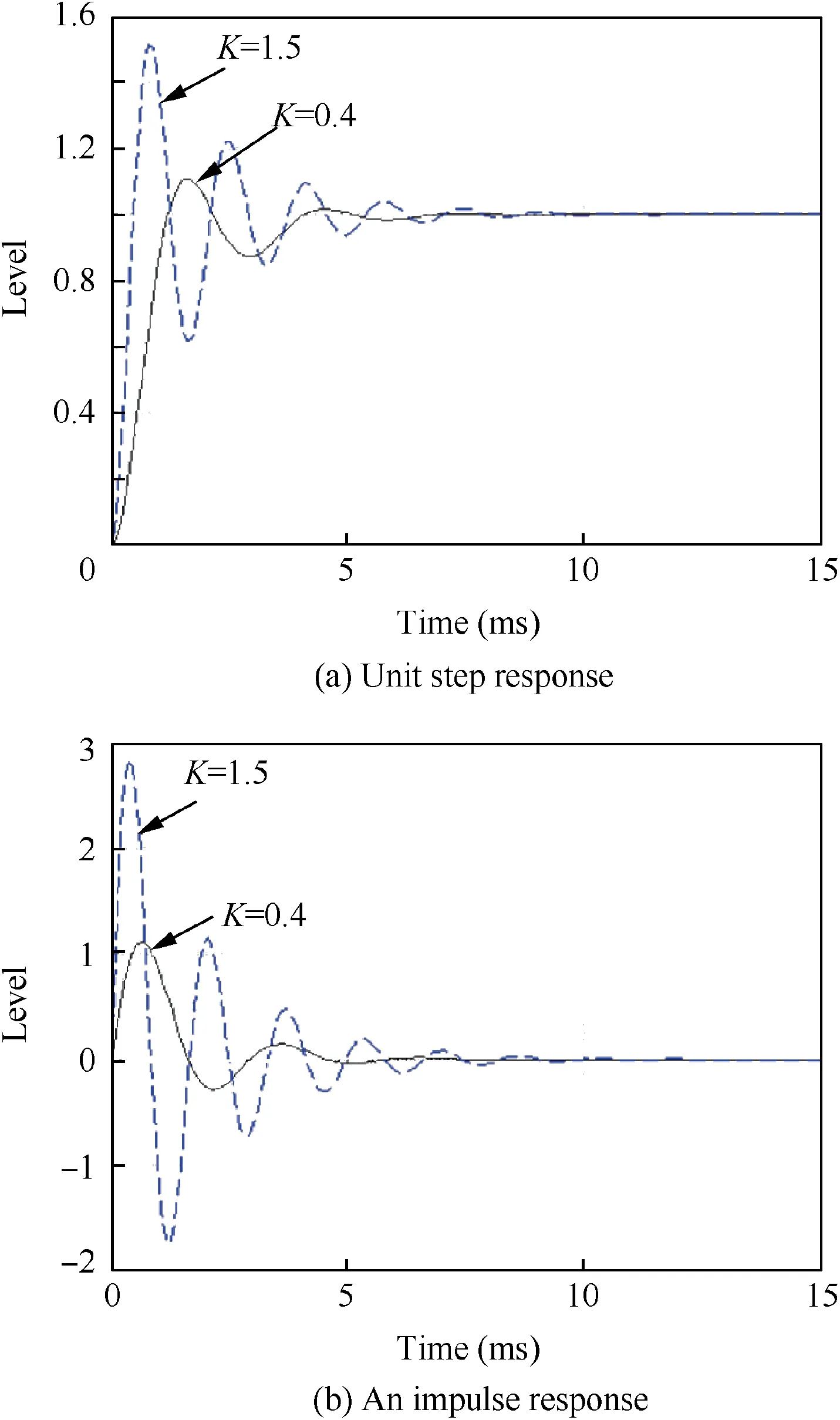
Fig. 11 Transient response for lead-lag compensator control of boundary layer system.
The tracking performance of the feedback control is determined by the transient response of the control system to a unit step and an impulse shown in Fig. 11. The effects of two proportional gains are compared.The step response of the system with the gain K=1.5 shows a very oscillatory response,as we might expect from the low PM due to large value of K.When K is reduced to 0.4 as designed value a substantial reduction in the oscillations is observed. The step response in Fig. 11(a)shows no steady-state error to a step input and the reasonable damping that we would expect from PM=45° at K=0.4.The impulse response in Fig.11(b)exhibits well damped behaviour and shows the integral control term eventually driving the disturbance error to zero after about 5 ms.
4.3. Performances of feedback control on boundary layer 3D TS wave cancellation
4.3.1. Transfer functions in time-domain and physical space
The performance of the feedback control system on the boundary layer control is determined by computing and displaying the response of the system to the external disturbances at x2,which is artificially introduced by the exciter at x0.In the practical implementation, all the signals detected are the waves in time domain. Therefore, based on Eq. (20) we calculate the actuator’s signal by convoluting the external disturbances n(t) with a time-domain transfer function gξ(t)

where * indicates convolution in time-domain and gξ(t) is the inverse Fourier transform of Gζ(ω), as given by

by replacing s in Eq. (18) with jω.
So far, due to the short distance between the actuator and the sensor A we only need to consider an uncoupled control mode with spanwise wavenumber β=0 for a practical reason.However,if a 3D case has to be considered when designing the control system, we would see that the process of determining the transfer function P12(s, β) and the parameters of the controller C(s, β) for each spanwise wave number β from 0 to 100 is identical to the 2D process. This process is complex and time consuming by using frequency-response method and we would suggest to apply state-space design method. In the physical phase we can get the gz(z, t) in β-space as
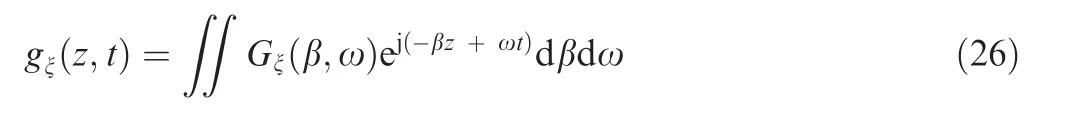
and the controller’s signal sC(z,t) driving the actuator takes the form of

Far downstream at the reference sensor B,the signal sB(z,t)along spanwise direction is
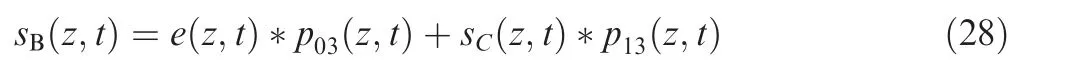
where e(z,t), p03(z,t) and p13(z,t) are the inverse Fourier transforms in physical space and time-domain of E(s), P03(s) and P13(s)respectively.This signal in time-domain is used to verify the performance of the feedback control scheme on the cancellation of the T-S waves in the boundary layer.
4.3.2. Cancellation of 3D disturbances using simple uncoupled control mode
Once the feedback controller is determined based on the plant boundary layer between the actuator and the downstream sensor A, the next step is to test the performance of the control system on the 3D T-S wave cancellation.Two types of 3D disturbances, i.e. a wavepacket and random noise, are selected.To generate the 3D random disturbances, an array of exciters driving by a broad band of frequencies is positioned across the span from z= -100 mm to z=+100 mm at 1 mm intervals. When the wavepacket is considered, only the exciter located on the center-line (z=0 mm) is activated and an impulse is applied.In order to account for the 3D characteristics of the disturbances, a multi-inputmultioutput feedback control system with sensors and actuators distributed spanwisely is constructed. The spanwise distribution of all the devices on the flat plate is shown in Fig. 12. The streamwise position of the sensor A is now set to x2=520 mm since the streamwise separation Δx21=20 mm.
The 3D full control mode described by Eqs.(26)and(27)is complicated, and it requires spanwise cross-linking of all the sensors A and the actuators, as shown in Fig. 12(a), so that each upstream actuator needs to use the information from the neighbouring sensors as well as the one directly downstream. This cross-linking is not realistic in practical applications, so we turn to the uncoupled control mode shown in Fig. 12(b) where each upstream actuator is connected only to the sensor directly downstream. The uncoupled transfer function is obtained directly from 2D modes where β=0,and the controller’s signal driving the actuators takes the form of
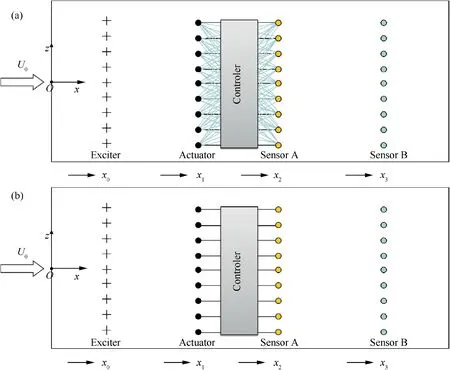
Fig. 12 Spanwise distribution of all devices on flat plate and connections of sensors A and actuators under full control mode (a) and uncoupled control mode (b), respectively. The streamwise position: x0=400 mm, x1=500 mm, x2=520 mm, x3=800 mm.

On the other hand,in any experiment we must consider the spanwise spacing Δz of the sensing and actuating devices since they are discretely and spanwisely positioned. The spanwise spacing of the devices must be able to resolve the 3D characteristics of any growing disturbances. With all these considerations and constraints, the cross-correlation coefficient σ between the original random disturbance and the controlled signal at the sensors B position x3=800 mm is shown in Table 1. It can be seen that a cross-correlation of 0.957 can be obtained with the spanwise spacing up to 20 mm. Correla-tion coefficient of 0.957 means that the mean square of the residue after cancellation is 0.08, or 2(1-σ), roughly amplitude reduction of 70%achieved with this simple uncoupled control mode. The corresponding result of using feedforward control mode by Li & Gaster3is also included in the table.Their control showed better performance than the current feedback control scheme, which can be understood because the transfer function of the controller in Ref.3had been optimised offline to give a better cancellation.
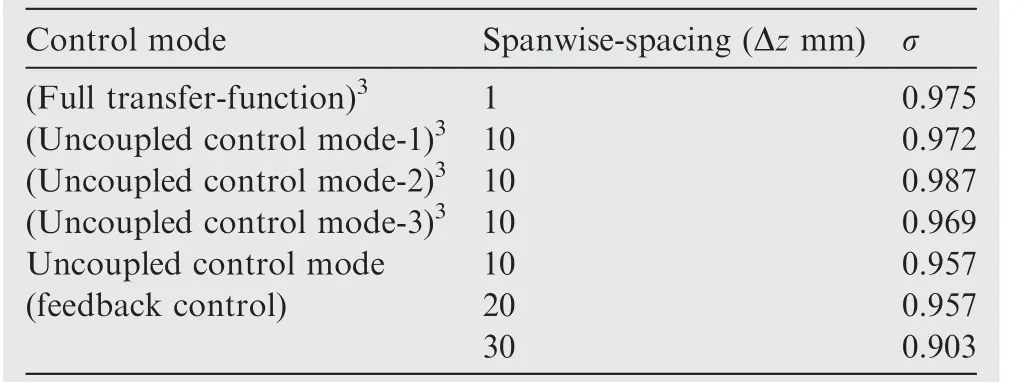
Table 1 Correlation coefficients σ between original random disturbances and controlled disturbances at x3=800 mm for different spanwise spacing of the sensors and the actuators.The results of using full control modes and feed forward control modes in Ref.3 are also included in the table.
Fig. 13 shows the resulting space-time wavepackets and random disturbances with and without feedback control at the streamwise position x3=800 mm. Here, the spanwise spacing is 10 mm,which is quite a practical one in experiments.Both the perturbations remaining in the boundary layer after cancellation shows that the dominant parts of the disturbances have been largely removed leaving only a small residue, indicating excellent T-S wave cancellation.Fig.14 shows the result signal after cancellation with sensors and actuators at different spanwise spacing. Below the spanwise spacing of 20 mm, the residue after cancellation is kept small, but the residue level increases rapidly when the spanwise spacing arrives at 30 mm.The poor control performance at larger spanwise spacing is due to the incapacity of the devices to resolve the 3D characteristics of growing disturbances.
5. Discussion

Fig. 13 Cancellation of the 3D wavepackets and random disturbances at x3=800 mm using the feedback controller.
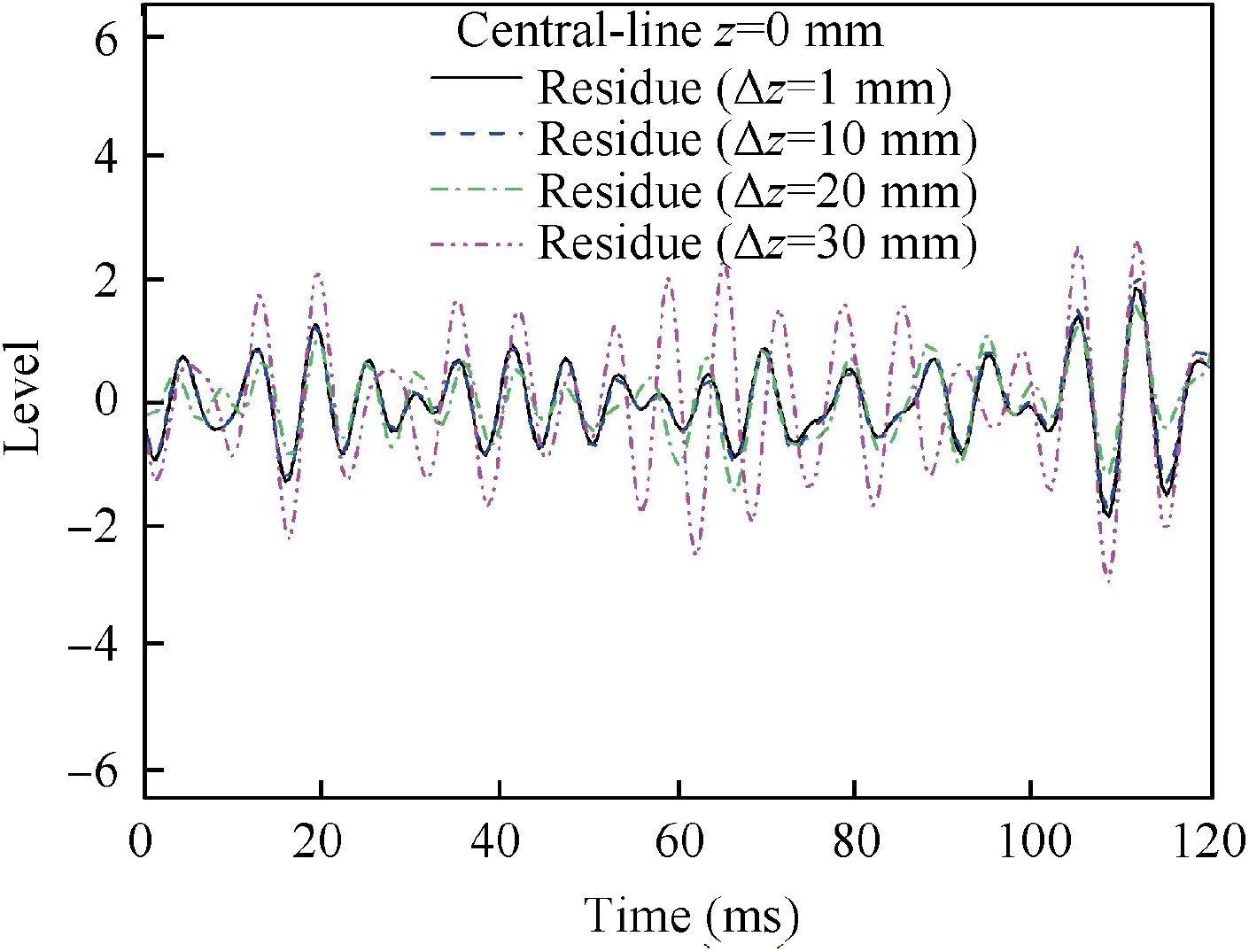
Fig. 14 Residue after feedback control with different spanwise spacings of the sensors and actuators.
The formulation of a feedback control of the spatially evolving instability T-S waves on a flat plate is analysed numerically and theoretically.It is shown that the dynamic model(transfer function)of the boundary layer flow can be obtained by linear stability calculation of the amplitudes and phases of the disturbances. An approximation using an uncoupled mode to the dynamic model is made using frequency-response method to capture those dynamics that have the greatest influences on the input-output behaviour of the boundary layer. With both this approximation and the considered flow conditions of Re=1000 based on the displacement thickness, low-order mathematical formulas of the dynamic model can be explicitly expressed for two short steamwise separations of 20 mm and 40 mm between the upstream actuator and the downstream sensor. Based on the simplified dynamic model, a feedback control system with a lead-lag compensator combining with a standard Smith predictor are designed. It is shown that this feedback control system can significantly reduce the perturbations in the boundary layer. To make the feedback control more realistic in practical applications, the uncoupled control model combining with limited number of spanwiselydistributed sensors and actuators are considered. Uncoupled control mode means that the upstream actuator is only connected to the sensor directly downstream, i.e. the actuatorsensor pair works independently. With this simple modelbased control strategy and a practical spanwise spacing between the sensors and the actuators, the 3D disturbances in the boundary layer can be largely suppressed, making the control itself realistic and competitive in the practical applications.
6. Concluding remarks
We have shown that a numerical approach can provide an essential tool for determining the geometries of transducers and for designing the required controller for feedback control of T-S waves in a boundary layer.In this numerical model,the actuator and the sensor are assumed to be ideal,i.e.,the output of the actuator generated in the boundary layer are the same amplitude and phase as the driving signal. However, in any practical implementation, due to different types of actuators,the driving signal of the actuator needs to be adapted so as to get the required cancellation,as we have seen in the control experiments in literatures.2,3,26Therefore, in experiments,except for the near-field sensor A, the far downstream sensor B’s signal in our case might also need to be fed back through an adapter to adjust the phase and amplitude of the actuator.In addition, streamwise-repeated control using the same feedback controller can be applied to further cancel the residue.Experimental investigation into the boundary layer T-S wave cancellation using the current designed feedback control and the possible design of an adapter is underway in a lowturbulence wind tunnel.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The investigation is made possible through the support provided by the Open Fund of Key Laboratory of Aerodynamic Noise Control of China (No: 1901ANCL20190105), which is gratefully acknowledged. The first author also thanks Professor Gaster (now at City, University of London) for providing original computer codes for T-S wave calculation.
 CHINESE JOURNAL OF AERONAUTICS2021年3期
CHINESE JOURNAL OF AERONAUTICS2021年3期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Criteria for hypersonic airbreathing propulsion and its experimental verification
- Effect of scavenge port angles on flow distribution and performance of swirl-loop scavenging in 2-stroke aircraft diesel engine
- Ship detection and classification from optical remote sensing images: A survey
- Variational method based robust adaptive control for a guided spinning rocket
- Inertial parameter estimation and control of non-cooperative target with unilateral contact constraint
- Theoretical modeling of vectoring dual synthetic jet based on regression analysis
