基于B 样条函数的快速波前复原

陈 浩，魏 凌，李恩德，何 益，杨金生，李喜琪，樊新龙，杨泽平，张雨东

1 中国科学院光电技术研究所，自适应光学重点实验室，四川 成都 610209；

2 中国科学院大学材料科学与光电子技术学院，北京 100049；

3 江苏材料光学重点实验室，江苏 苏州 215163；

4 中国科学院苏州生物医学工程技术研究所，江苏 苏州 215163

1 引 言

夏克-哈特曼波前传感器(Shack-Hartmann wavefront sensor，简称哈特曼)是一种常用的斜率型波前探测器，被广泛应用于自适应光学的相关领域[1-3]。它并不能直接探测波前的相位信息，只能通过子孔径内的斜率重构波前相位。由于传感器的噪声、采样误差、子孔径内存在高阶像差等原因，斜率的计算易受噪声影响。尽管可以提高斜率计算的精度和抗噪能力[4-5]，为复原计算提供更精确的输入，然而，斜率探测误差是不能完全消除的，这需要波前复原算法具有抗噪能力。因此，波前复原算法需要综合考虑抗噪性、准确度和计算复杂性。常见的复原算法可以分为两类：区域法和模式法。

区域法在待测波前点与斜率测量点之间建立差分模型，然后通过求解线性的差分方程组复原波前信息，传统的区域法模型有Fried[6]和Southwell[7]等。这种方法具有良好的局部性，可以较精确地复原局部区域的像差，并且可以用于任意形状的光瞳。然而由于差分模型的精度及差分过程导致的误差，算法抗噪能力较弱。另外，由于差分模型的限制，复原的波前点数量与子孔径数量相当，需要通过插值来获得高空间分辨率的波前信息，而这会带来额外的误差。

模式法一般采用空间正交多项式复原波前。最常用的是Zernike 多项式，因为它与Seidel 像差有非常直接的对应关系[8]。模式法复原的波前具有解析表达式，可以得到任意空间分辨率的波前信息。由于Zernike多项式只在圆域内正交，因此只能复原圆形光瞳的波前，不少学者采用变换等方式使Zernike 可以适用于方形或其它形状的光瞳[9]，但仍存在变换复杂，不能完全适用于所有形状光瞳的缺点。另外，尽管Zernike多项式在圆域内是正交的，但其导数并不正交，即各个模式的斜率不正交，因此会发生模式泄露，并且在不同阶次的Zernike 空间中，展开系数是不一样的。Nam 等[10]提出正交化斜率矩阵的方法来解决这个问题，但此时的解空间已不再是原本的Zernike 空间了。另外，由于正交多项式的非局部性，导致任一子孔径的斜率可能会对所有的模式产生影响，对边界上的波前复原精度较差，因此模式法不能很好地复原局部区域的像差。由于多项式的正交性，模式法一般适用于圆形光瞳或方形光瞳，当光瞳形状与预设不一致时，复原精度会受到比较严重的影响。

在高能激光[3]、光学加工检测[11]以及基于像差的PSF 计算[12]等应用中，对局部像差的复原能力要求相对较高，而基于Zernike 多项式的模式法由于局部性较差，并且复原的像差容易在边缘出现较大的值，在这些场合应用有限。

为了保证复原的局部性同时提高抗噪能力，样条函数的方法得到了广泛的应用。Seifert 等提出了一种采用三次B 样条进行波前复原的方法[13]，该方法用二维三次样条曲面对波前进行最小二乘拟合。由于B 样条曲面的平滑性和紧支撑特性，可以在保留局部性特征的同时，具有比传统区域法更强的抗噪声能力。文章仿真结果表明，随着样条数量的增多，局部复原精度越高，但当样条数量接近斜率采样点数量时，复原矩阵的条件数会增大，复原精度会有所下降。然而文章并未明确B 样条数量的选择方法，只是建议针对应用场合的像差仿真来确定最优样条数量。Ares 定量比较了三次B 样条波前复原算法与Zernike 模式法的性能区别[14]，证实了对于复杂的波前，三次B 样条复原方法更具有优势。随后，Cornelis 等提出了基于多变量的非线性样条波前重构方法(spline based aberration reconstruction,SABRE)[15]，该方法本质上属于区域法，通过特定的三角形分割方式，采用样条函数空间模型代替常规的差分模型，该方法可以适用于任意形状的光瞳和任意的子孔径布局。SABRE 方法在模型划分时，有多种分割模型，不同分割模型的复原精度也不尽相同，而文章中并未提出分割模型的选择方法。Huang 等提出了一种使用局部化的三次样条函数复原波前的方法[16]，尽管能提高局部复原精度，但也更容易受到噪声的影响。Pant 使用加权的三次样条函数复原波前[17]，在提高算法抗噪能力的同时也提高了算法计算复杂度。

从以上文章可以看出，相比普通样条函数，B 样条函数在控制点处均具有相同的样条基函数，在抗噪能力和局部复原能力上均衡，计算复杂度也较小。本文以2 阶B 样条为例，提出了一种基于B 样条函数的快速波前复原算法，并将原本的斜率最小二乘化问题转化为泊松方程，然后使用超松驰迭代法进行求解，大大减少算法的存储需求和计算量，若使用分块加速超松驰迭代法，还可以提高算法的并行程度，方便应用到多核PC 系统、FPGA 或DSP 等硬件平台上。

本文结构如下：第二节介绍基于B 样条的波前重构算法；第三节介绍基于泊松方程的2 阶B 样条快速复原算法；第四节通过对驱动器响应函数测试的实验，将本算法与传统波前重建算法进行比较；第五节对全文进行总结和展望。

2 基于B样条的哈特曼波前快速复原算法

2.1 哈特曼基本原理

哈特曼波前传感器通过微透镜阵列、小孔或光栅等光学元件，将待测波前分割为N个小区域后，每个区域会在CCD 上成像。当待测量波前与参考波前存在偏差时，这个偏差会转化为子孔径内光斑的偏移(Δx,Δy)i,i=1,2,...,N，令波前为φ，微透镜焦距为f，则有：

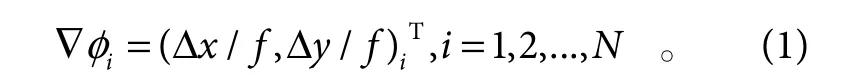
波前重构算法即是通过采样到的{∇φi}复原出波前φ。

2.2 B 样条曲线

B 样条(Basis spline)最初由Isaac Jacob Schoenberg提出，其具有几何不变性、凸包性、保凸性、局部支撑性等优良特性，是应用最广泛的样条函数之一[18]。

k阶B 样条曲面方程可表示为

其中：i和j为节点序号，为控制顶点，Ni,k及Nj,k为k次规范B 样条基函数，基函数为次分段多项式，可由递推公式得到：

定义u i=i，即均匀采样的情况，则可以得到1 阶和2 阶B 样条基函数分别为

图1 绘制了控制节点间隔为1 的1 阶和2 阶B 样条基曲面。

2.3 基于2 阶B 样条基曲面的波前复原

为简化表述，令：

图1 B 样条基曲面。(a) 1 阶B 样条基曲面；(b) 2 阶B 样条基曲面Fig.1 Surfaces of B-spline basis.(a) First-order B-spline surface;(b) Second-order B-spline surface

易知B(x,y) 为关于原点对称的函数。由2.2 节知，B(x,y)具有紧支撑特性，通过将像差波面分解为一系列B(x,y) 波面的叠加，可以在有效抑制噪声的基础上更好地复原局部波前。

为使B 样条复原的空间频率最高，需要B 样条基的数量不少于波前采样点的数量，对于方形布局的微透镜阵列，在传统的区域法中，有两种常用的模型可以借鉴——Fried 模型和Southwell 模型。

图2 描述了这两种模型的B 样条基位置与子孔径之间的关系。其中灰色圆圈表示样条基的位置，正方形为子孔径位置，正方形内的正交箭头为子孔径内斜率。

假设子孔径数量为(M×N)，为达到最优的空间分辨率，在 Fried 模型中，B 样条基数量为(M+1）× (N+1)，Southwell 模型中，由于B(0,0)=0，需要在上下左右至少分别补充1 排B 样条基，即B 样条基的数量最少为(M+2）× (N+2)。

以子孔径边长为单位，令左上角坐标为(0,0)，则Fried 模型和Southwell 模型排布的B 样条基分别如式(7)和式(8)所示：

代入式(1)，则对于每个子孔径有：

图2 方形排布的B 样条基位置与子孔径之间的关系。(a) Fried；(b) SouthwellFig.2 Positional relation between B-spline basis and subaperture with a square layout.(a) Fried model;(b) Southwell model

由于B(x,y) 的紧支撑特性，R为一稀疏矩阵，因此式(12)为稀疏方程。

易知，若B(x,y) 使用1 次B 样条函数，式(12)与传统的Fried 区域法一致，而Southwell 布局也有类似的关系，因此传统的区域法可以视为B 样条函数复原算法在1 阶条件下的特例。为了描述简洁，本文后面的讨论和仿真均采用Fried 模型，而Southwell 模型推导方式与之类似。

3 基于泊松方程的快速2 阶B 样条函数波前复原算法

式(12)的直接解法为求解R的广义逆矩阵，即

尽管R为一个稀疏矩阵，但R的广义逆矩阵R+并不是稀疏矩阵，在复原的时候即使提前计算好R+，也需要(M+1）2× (N+1)2个数的存储空间，并且一次重构需要(M+1）2× (N+1)2次乘法。当子孔径数目比较多的时候，使用FPGA 或DSP 等计算时，会带来巨大的空间开销，可以预估，当子孔径数提升1 倍时，存储空间和计算量会提升16 倍，这种情况下，这种计算方法将制约B 样条波前复原算法的应用。

由式(10)知，波前重构是求解如下最优化问题：

代入式(10)，可得：

图3 B 样条散度积分示意图Fig.3 B-spline divergence integral diagram

式(19)左边等价于计算图3 中编号为5 的B 样条基处的散度(其中圆圈代表B 样条基位置，实线方形表示子孔径区域，虚线方形表示B 样条基的积分区域)，支撑域包含编号5 区域的B 样条基为1～9 号，对ΔBi(x,y)(i=1,2,…,9)的解析表达式在编号5 区域中积分，式(19)可改写为

改变成式(20)后，即可使用逐次超松驰迭代法(successive over relaxation method,SOR)进行求解[19]：

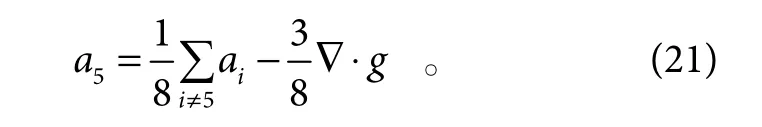
接下来计算∇⋅g。为方便描述，以图4 所示为1,2,3,4 表示4 个子孔径，令为子孔径x和y方向的斜率，为计算黑色圆点处的散度∇⋅g，在黑色圆点处对斜率进行1 阶Taylor 展开，可得：

进一步可得出：

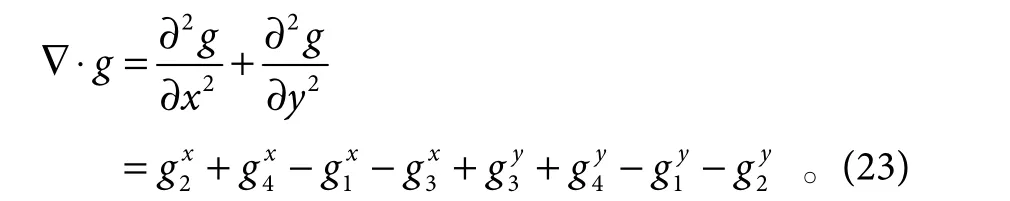
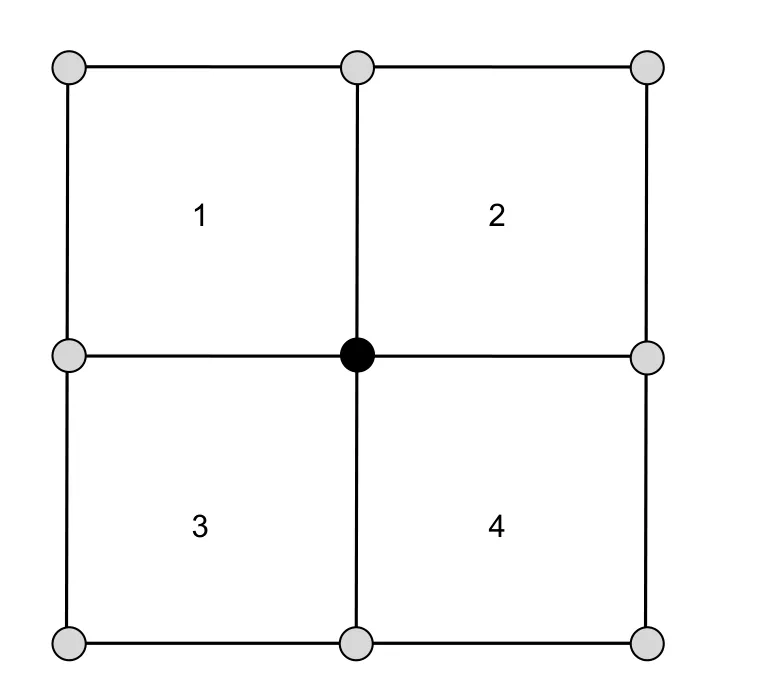
图4 散度近似计算示意图Fig.4 Diagram of divergence approximation

这样就可以通过子孔径的斜率估计出B 样条基处(黑色圆点)的散度。至此，式(19)中的必要元素已具备。通过求解式(19)，则可得到所有B 样条基的系数，最后通过式(9)则可得到复原波前的解析式。

对于边界位置B 样条基，由于积分区域改变，式(20)会有所改变，以图3 中的1 号B 样条基为例：

而边界位置处的散度估计，可以通过对斜率的外拓来简化计算，可采用重复延拓或补0 延拓。

可见，基于泊松方程的2 阶B 样条快速重建算法，存储空间为(M+1）× (N+1)，乘法需求量为(M+1）× (N+1)×L，其中L为迭代步数。一般而言，SOC 算法在迭代几十次左右后将收敛。因此相比广义逆求解，存储空间和计算量的需求减少了很多，特别当子孔径数目增大时，优势更明显。

4 实 验

本文利用自主研制的121 单元六边形排布的压电陶瓷变形镜，测量其中心位置处7 个驱动器(命名为1～7 号，正中心位置为4 号)的响应函数，分别通过干涉仪和哈特曼波前传感器采集数据，再通过不同的复原算法从哈特曼的数据中复原波前，并与干涉仪的数据进行对比。

为减少变形镜初始面型以及光学系统对测试结果的影响，每个驱动器分别加±80 V 后，对测量得到的波前进行对减。基准数据采用干涉仪(Zygo GPI-600)测量的结果，4 号驱动器的响应函数如图5 所示。

使用哈特曼测量时，将变形镜的光瞳口径缩束后与哈特曼波前传感器成3：4 匹配(即哈特曼波前传感器的有效探测区域为变形镜的75%)，哈特曼波前传感器的微透镜阵列为方形排布，阵列数为22×22，子孔径大小为0.25 μm，焦距为9.52 mm(使用Yang 等提出方法标定[20])，测量波长为808 nm。

通过区域法、模式法和本文提出的复原算法(迭代次数取20 次)复原的波前和残差波前如图6 所示，为实现相同数字采样率，区域法的结果采用双线性插值方法进行处理。为实现对减，首先通过相关找到原始两个波面的位置偏移，区域法通过双线性插值重新生成与干涉仪位置一样的波前；模式法和本文提出的算法通过偏移后的坐标计算波前，考虑到模式法的边缘效应，仅计算单位圆域内的波前数据，而本文提出的算法仅计算样条内部的区域。4 号驱动器的复原波前和残差如图6 所示，相关系数、残差如表1 所示，所有驱动器的波前残差PV 值与RMS 值如图7 所示，对应的数值结果如表2 所示。

从与干涉仪对比的结果可知，由于Zernike 模式法的局限性，其对局部像差的复原能力较差，因此对这种驱动器产生的响应函数无法精确复原，复原残差很大。区域法和本文提出的方法均可以较好地复原这种局部像差。从复原的数值上看，本文的方法优于区域法，其原因在于：区域法采用双线性插值时会带来插值误差；区域法的抗噪能力有限，因此残差波前的PV 值显著大于本文提出的方法。另外，观察图6 中驱动器顶端复原的波前细节，可以看出，区域法在这个位置由于受采样误差和噪声的影响，未能复原出平滑的“峰”。

图5 4 号驱动器的干涉仪测量数据Fig.5 Measurement data of No.4 actuator obtained with ZYGO interferometer

图6 不同复原方法复原结果。(a) 本文算法重建波前；(b) 本文算法的残余波前；(c) 基于Zernike 多项式的模式法重建波前；(d) 模式法的残余波前；(e) Fried 区域法重建波前；(f) 区域法的残余波前Fig.6 Wavefronts restored by different methods.(a) Wavefront restored by our method;(b) Residual wavefront error of (a);(c) Wavefront restored by the modal method;(d) Residual wavefront error of (c);(e) Wavefront restored by the zonal method;(f) Residual wavefront error of (e)

表1 不同复原方法结果比较(4#驱动器)Table 1 Comparison results of different wavefront reconstruction methods

图7 不同驱动器复原残差Fig.7 PV and RMS results of residual wavefront reconstructed by different methods

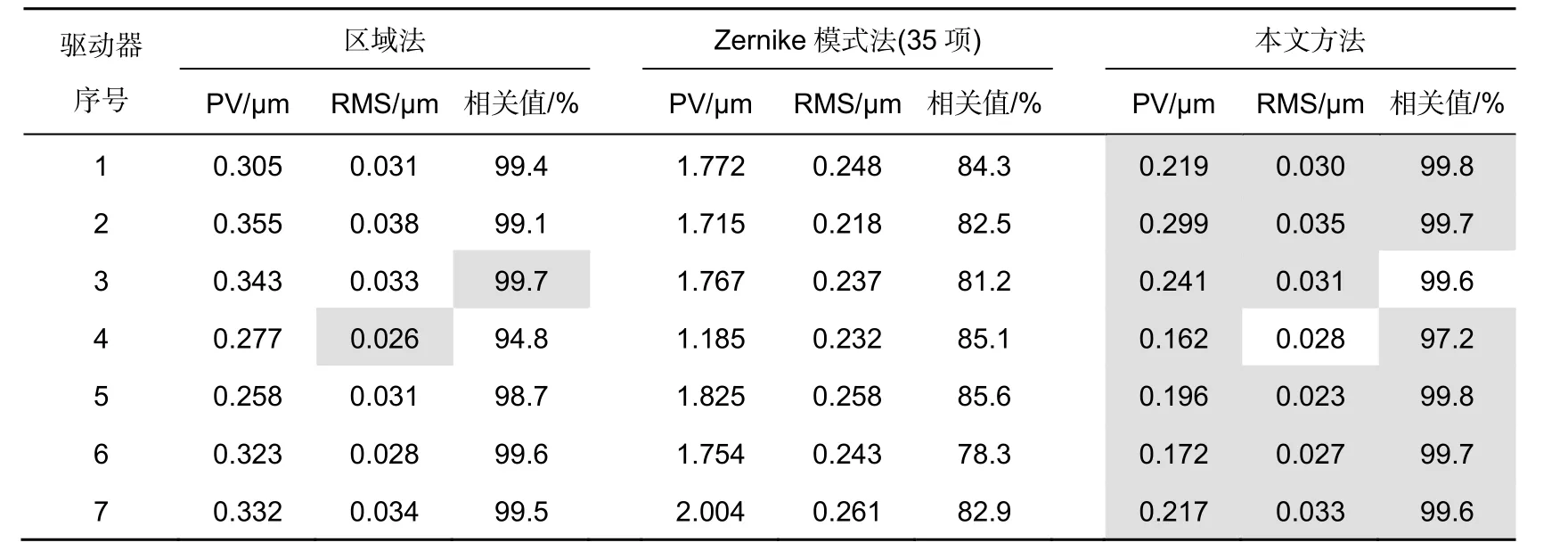
表2 不同驱动器复原残差及相关值Table 2 Residual reconstruction error and correlation values of different actuators

5 结 论

本文提出了一种基于2 阶B 样条快速波前复原算法，采用泊松方程改写斜率最小二乘方程，使其可以通过超松驰迭代法进行快速求解，大大降低了复原算法的存储空间需求和计算复杂度，容易在DSP 或FPGA 等硬件中实现，在子孔径数目增多时其优势更加明显，并且可以采用分块的超松驰迭代法等方法[21]提高算法的并行计算能力。该方法可以推广到其它斜率型波前传感器，如金字塔波前传感器[22]，四波剪切干涉仪[23]等。

通过对变形镜驱动器响应波前的测量实验可以看出，模式法存在明显的局限性，无法精确复原局部像差，而本文提出的算法具有与区域法相当的局部像差复原能力，同时有优于后者的抗噪能力。由于复原的波前具有解析解，无需插值即可得到非常高的数值采样精度的波前信息，这使得复原波前更加平滑。

通过泊松方程改写的式(19)，左侧为对样条函数的散度积分，右侧为利用斜率对散度的估计。因此，左侧可以扩展到不同阶次和不同扩展度的B 样条基，实现数值采样精度的灵活选取。而右侧根据式(23)中的处理方法，可以灵活选取计算散度的区域。一般来说，计算散度利用的斜率点越多，抗噪能力越强，对局部像差的复原能力越弱。因此，通过灵活选取计算散度的区域，可以有效平衡对局部区域像差的复原能力和抗噪能力需求。