一道三角题的多重“收益”

华东师范大学第二附属中学 高三（6）班 邱 天

寒假要减少走亲访友，我只能来拜访这些对我不离不弃的“趣题兄弟”.不曾想还真的有意外收益呢.

表面看来非常有意思：已知条件都是余弦相关形式，且各出现两次，而欲证则是纯角的形式，三个角可以组成一个三角形.

问题1：设α,β,γ均为锐角，且cos2α+cos2β+cos2γ+2cosαc osβc osγ=1.求证：α+β+γ=π.

难点所在：题设中共有三个字母变量，由于不知道α,β,γ之间的数量关系，故而仅仅利用三角恒等式来推导结论，解题方向是不明确的.

收益1：问题1 的分析与证明

注意到条件中等式左边是完全对称式，可以选择某一个（如cosγ）为变量（主元），以另外两个（cosα,cosβ）为参数（辅元），于是原等式可视为关于cosγ的一元二次方程

cos2γ+(2cosαc osβ) cosγ+cos2α+c os2β-1=0.①

方程的判别式Δ=4cos2αc os2β-4(c os2α+cos2β-1).

敲黑板

思维受阻时，不妨做目标分析.

接下来如何化简整理判断式？

思维受阻，分析目标：

要证α+β+γ=π，即γ=π-α-β.

而余弦函数在(0,π)上单调递减，由条件知γ,π-α-β∈ (0,π)，

故只要证cosγ=cos(π-α-β)，

即证cosγ=-cos(α+β)=②

而方程①的根为cosγ=考虑到α,β,γ均为锐角，故cosγ=与②式比较知，只需证Δ=4sin2αs in2β.

思路总结：一方面将条件视为一元二次方程来分析，另一方面从要证的结论倒推，“从两边推中间”，将问题1 的解决聚焦于判别式的化简.

至此思路已经完全打通，但感觉意犹未尽啊！由于计算不太烦杂，我做了点符号上的变化，几番探索终得收获：

收益2：问题1 的等价形式

等价问题：设α,β,γ均为钝角，且cos2α+cos2β+cos2γ-2 cosαc osβc osγ=1.求证：α+β+γ=2π.

分析1：令α0=π-α,β0=π-β,γ0=π-γ，则α0,β0,γ0均为锐角.

条件等式等价于

cos2α0+cos2β0+cos2γ0+2 cosα0cosβ0cosγ0=1.

意外之喜：任老师在获悉我研究的这道题后，向我推荐了唐立华老师的《向量与立体几何》一书，于是有了“分析2”这个意外之喜.

由问题1 的结论，知α0+β0+γ0=π，即α+β+γ=2π.

分析2：设三棱锥P-ABC的三条侧棱PA,PB,PC的长度分别为a,b,c，三条侧棱两两所成的面角分别为α,β,γ，则体积为③

当1-cos2α-cos2β-cos2γ+2 cosαc osβc osγ=0时，三 棱锥体积V=0，此时三棱锥顶点P落到底面△ABC内部（即三棱锥的高为0），于是α+β+γ=2π.

欣喜之余：虽然是“误打误撞”，但不得不说，以三棱锥体积（的极端情形）作为桥梁，沟通条件中的三角等式与目标结论α+β+γ=2π，反映了数学分支之间丰富而有趣的内在联系.

另外，“老套路”逆命题是否也成立呢？

收益3：问题1 的逆向问题

逆向问题：已知α+β+γ=π，求证：cos2α+cos2β+cos2γ+2 cosαcosβcosγ=1.

利用三角恒等式，即可得到下面的证明.

cos2α+cos2β+cos2γ+2 cosαcosβcosγ-1=cos2α+cos2β+cos2γ+[cos(α+β)+cos(α-β)]cosγ-1,

由条件α+β+γ=π ⇔γ=π-α-β,故

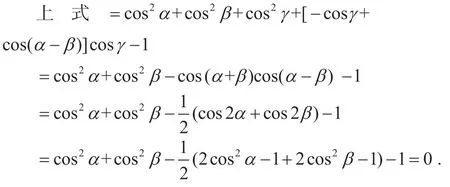
至此大功告成，酣畅淋漓.多重“收益”，成就满满！

当然，“强行”引入正弦，在△ABC中，令γ=π-C，也有相关结论：sin2A+sin2B+cos2C-2sinAsinBcosC=1.