刚性钝头弹体正贯穿中厚金属靶的挤凿块速度模型

孙永壮，吕中杰，刘 彦，黄风雷

(北京理工大学 机电学院，北京 100081)

刚性钝头弹体贯穿中厚金属靶，靶板材料发生挤凿破坏，形成与弹体截面大小相近的挤凿块，挤凿块与弹体以一定速度射出，对靶后目标形成有效毁伤[1]。以往大多弹体余速计算的经验公式，包括Recht等[2]以能量守恒为基础的挤凿破坏理论均认为挤凿块速度与弹体余速相同。然而，对于刚性钝头弹体贯穿中厚金属靶后射出的挤凿块而言，根据靶板材料不同，弹体和挤凿块会出现粘连和分离两种不同情况。当刚性钝头弹体冲击的靶板材料为强度和硬度较低且软的低碳钢时，挤凿块会与穿靶后的弹体粘连在一起，例如，Pradhan等[3]通过直径10 mm刚性球形弹体冲击4 mm厚低碳钢板实验结果表明挤凿块黏结在球形弹体上的，此时低碳钢靶板射出的挤凿块的速度与弹体余速相同；相反，在更多的弹靶情况下，如当靶板材料为强度和硬度较高且脆的铝合金板以及高强钢板时，挤凿块与弹体是分离的，其速度将不同于弹体余速，此时若仍将挤凿块速度与弹体余速视为相等是不恰当的。

肖新科[4]以材料为38CrSi的平头圆柱弹体撞击5 mm厚Q235钢靶板，司马玉洲等[5]以材质为9CrSi的平头弹体撞击7A04-T6铝合金靶板，实验结果均表明靶后的挤凿块与弹体是分离的。Børvik等[6-7]通过刚性钝头弹体撞击Weldox 460 E钢板实验得到挤凿块速度明显大于弹体余速的实验数据，且认为断裂后挤凿块速度的突然增加是由弹丸和挤凿块中的应力波引起的。Børvik等[8]实验研究了平头、半球形头和尖头三种不同头部的弹体侵彻12 mm厚的Weldox 460 E钢板，其中平头和半球形头弹体在侵彻过程中形成了挤凿块，且挤凿块的速度均高于弹体余速，但半球形头弹体形成的杯状挤凿块质量明显小于平头弹体在侵彻过程中形成的柱状挤凿块质量，这种质量的差异必定会影响其速度。另外，挤凿块更高的速度意味着在穿靶后拥有较大的动能，其对靶后目标产生的毁伤不容忽视，因此对刚性钝头弹体在贯穿金属靶后的挤凿块速度模型建立显得尤为重要，可以通过该模型定量计算刚性钝头弹体对靶后目标产生毁伤的能力。

将挤凿块速度和弹体余速分开考虑，提出了一显式的挤凿块速度模型。根据穿甲过程中的能量守恒定律得出挤凿块速度与弹体余速的关系，通过不同形状的弹体在穿甲后射出的挤凿块形状和速度不同，改进剪切冲塞模型使其适用于平头、半球头弹体以及球形弹体，并基于改进后的剪切冲塞模型和挤凿块速度与弹体余速关系建立适用于中厚金属靶的挤凿块速度模型。通过直径8 mm钨球冲击3 mm厚GH4169靶板以及文献[8]中直径20 mm平头和半球形头弹体贯穿12 mm厚Weldox 460 E钢板的实验数据验证挤凿块速度模型，模型计算结果与实验数据具有很好的一致性。挤凿块速度模型结合挤凿块质量计算可实现对弹体贯穿中厚金属靶所形成的挤凿块毁伤能力的定量描述，并对多层间隔靶的穿甲研究提供一定的理论支撑。

1 挤凿块速度模型

1.1 挤凿块速度与弹体余速关系

对于强度和硬度较高且脆的靶板材料，在弹体冲击靶板整个过程中，将弹体余速Vr和挤凿块速度Vs分开来考虑，假设弹体无质量损耗，根据能量守恒[9]有

(1)

式中：mp为弹体质量；Vi为弹体初速；ms为挤凿块质量；Ws为和弹体剪切靶板所消耗的能量(剪切功)；Ed为关于变形和热的能量(塑性功)。在一定的弹靶条件下(即mp，ms和弹道极限速度V50均为常量)，式(1)中Ws为一常量而Ed仅与弹体初速有关

(2)

(3)

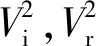
(4)

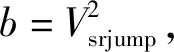
(5)

式中：k为与弹靶条件相关的常数；Vsrjump为弹体余速等于0时挤凿块速度相对于弹体余速的跳跃值，弹体余速本身存在速度跳跃即弹体余速不可能等于0，在实际实验中并不存在，因此Vsrjump只用于描述弹体余速与挤凿块速度的关系。

1.2 建立挤凿块速度模型

挤凿破坏是弹体把靶板中大小和弹体截面差不多的一块挤凿出去造成的，中厚金属靶受到钝头弹体撞击时，最易发生挤凿破坏。当弹体挤压靶板局部时，靶板局部与主体相连接的环形截面上产生很大的剪应力，由此突然产生的剪应变发出热量，在短暂的撞击过程中这些热量来不及逸散，从而大大提高了局部环形区域的温度，降低了材料的抗剪强度，以致出现挤凿型破坏，这是一个近似绝热剪断过程。

在弹体对靶板挤凿破坏理论方面有关弹体余速的研究已较充分。Recht等基于动量守恒和能量守恒提出了较为深入的Recht-Ipson模型来估计平头弹体(长径比约等于1)穿靶后的剩余速度。在Recht-Ipson能量守恒模型的基础上，Chen等[11-12]利用刚塑性分析和动态空腔膨胀理论，并将局部撞击响应和整体结构响应相结合，建立了适用于刚性平头弹体对金属靶板的剪切冲塞模型，得到了平头弹体对中厚金属靶剩余速度的理论公式

(6)

式(6)即为剪切冲塞模型，式中：V50为弹道极限速度；Vrjump为当弹体初速等于弹道极限速度时弹体剩余速度的跳跃值，因此挤凿块速度的跳跃值Vsjump=Vsrjump+Vrjump；η为无量纲质量等于挤凿块质量与弹体质量的比值，如式(7)所示。

平头弹体贯穿中厚金属靶形成的挤凿块直径一般与弹体直径相等，而球形及半球形头弹体相对平头弹体对靶板的剪切区域更小，所形成的杯状挤凿块的上下底面直径均明显小于弹体直径。对于平头弹体贯穿中厚金属靶形成的柱状挤凿块来说无量纲质量取式(7a)。对于球形弹体和半球形头弹体冲击中厚金属靶，起初撞击点附近受到拉力作用形成强烈的拉伸应变区域并在撞击点背部形成凸起，但此时没有发生剪切。随着变形的继续，拉伸区域中的材料出现颈缩，同时弹体与靶板的接触面也越来越大，此时接近于平头弹体撞击靶板的情况，靶板开始遭受剪切破坏且剪切区域相比弹体直径较小，射出直径小于弹径的杯状挤凿块。最终，中厚金属靶产生带有凹坑和鼓包的杯状挤凿块，将其等效为一个圆台以便计算挤凿块质量，并对无量纲质量η进行改进。因此，对于球形弹体和半球形头弹体贯穿中厚金属靶形成的杯状挤凿块来说无量纲质量取式(7b)。综上，式(6)中无量纲量η定义是

(7a)

(7b)

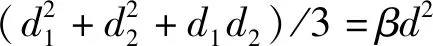
对于中厚金属靶，式(6)中无量纲量ϑ定义是[13]

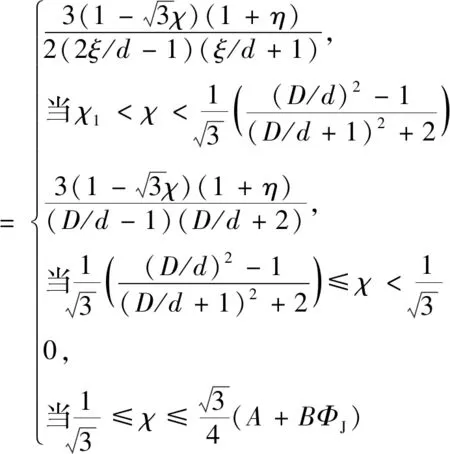
(8)

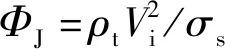
(9)

式(9)即为刚性钝头弹体正贯穿中厚金属靶的挤凿块速度模型，其中无量纲量η和ϑ的取值分别依据式(7)和式(8)。可利用挤凿块速度模型对刚性钝头弹体(平头、半球形头、球形)穿靶后射出的挤凿块速度进行计算。

当刚性钝头弹体贯穿多层间隔靶中前一层靶板时，挤凿块速度模型可对下一层靶板所受到的挤凿块冲击工况进行计算，即挤凿块速度模型可用于计算挤凿块对靶后目标的毁伤能力。一些具有重要战略价值的军事目标都使用多层防护结构，如大型舰船或者航空母舰普遍采用多层间隔式的防护结构，即层间具有一定间隙的间隔靶。

2 钨球正冲击GH4169中厚靶实验

挤凿块速度模型中涉及到的平头弹体和半球形头弹体贯穿中厚金属靶的弹体速度和挤凿块速度数据可直接从文献[8]中提取。为获得球形弹体贯穿中厚金属靶的实验数据，进行钨球正冲击GH4169中厚靶实验。GH4169属镍基高温合金常温和高温时都具有良好的机械性能，其相近美国牌号Inconel 718合金在GE生产的CF6发动机所有加工成形的零部件材料中所占质量分数达到34%，某些年份在GE所有发动机产品关键旋转类零部件中Inconel 718材料所占质量分数一直高居60%～70%[15]，GH4169(Inconel 718)材料广泛用于制造航空发动机和固体火箭发动机的热端部件等。由于钨合金球形弹体密度大且具有较高的存速能力和优越的侵彻性能，已成为杀伤战斗部的首选毁伤元素[16]。因此研究钨球贯穿GH4169中厚靶射出的挤凿块速度数据不仅可用来验证挤凿块速度模型，同时对航空发动机的毁伤能力评估也十分重要。

2.1 实验设计

实验设备的布置示意图设计如图1所示，实验设备包括12.7 mm弹道枪、标尺、靶板、高速摄影和破片回收装置，具体试验场地布置和靶板安装如图2所示。钨合金球形弹体的速度加载通过北京理工大学东花园试验基地的弹道枪实验平台实现，该弹道枪身管长度1.5 m，口径为12.7 mm，采用制式发射药和12.7 mm制式药筒，钨球和药筒之间用尼龙弹托连接。靶板四角与靶架用G型夹固连，用装满细沙的硬纸箱作为弹体和挤凿块的软回收装置。由于需要同时获得弹体余速和挤凿块速度，遂使用高速摄相机FASTCAM SA5(fps设置为42 000)监控整个撞击过程并测试弹体的初始速度、剩余速度以及挤凿块速度。在弹道平面内放置两把标尺，可对高速摄影测速作尺寸参考。

图2 实验设备布置Fig.2 Experimental equipment layout

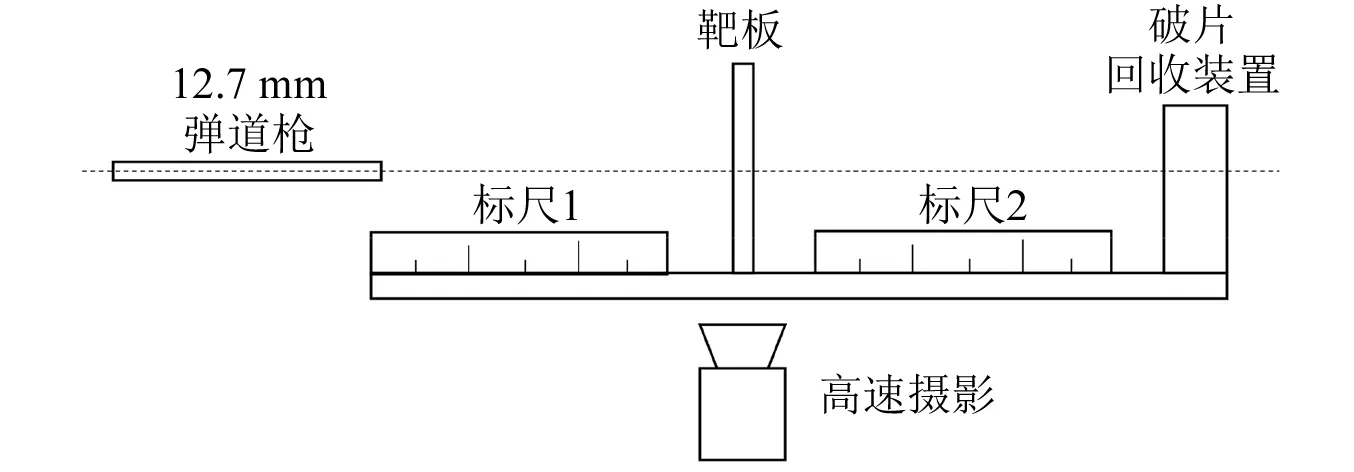
图1 实验设备布置示意图Fig.1 Sketch of experimental equipment layout

钨合金球形弹体材料为典型的钨合金W152(93钨)，直径8 mm。镍基高温合金GH4169厚度3 mm，产自东北特钢，3 mm厚靶板对于直径8 mm的弹体属于中厚金属靶，实验中靶板具体的力学性能、物理特性见表1。(执行标准：GB/T 14992—2005)

表1 GH4169(固溶处理)的物理和力学性能[17]Tab 1 Physical and mechanical properties of GH4169(solution treatment)[17]

为了实验方案的设计以及更快逼近弹道极限速度，需要对靶板的弹道极限速度进行预估。高润芳等[18]通过几种钨合金弹体正侵彻装甲钢板的实验，得到3 g钨球对10 mm厚装甲钢板的弹道极限速度为960 m/s，而3 g钨柱的弹道极限速度随着靶姿态的不同为916～1 011 m/s。因此，相同质量钨柱的弹道极限速度在钨球弹道极限速度一定范围内上下浮动，因此相同质量的球形和柱形弹体对靶板的弹道极限速度影响不大。Pereira等[19]给出了柱状Ti-6-4(底面直径12.7 mm，高25.4 mm)冲击面密度8.35 kg/m2Inconel 718的弹道极限速度为192 m/s，弹道极限能量为260 J。基于文献[19]及不同弹靶系统之间弹体对相同面密度靶板的弹道极限比动能等效准则[20]来预估本实验的弹道极限

(10)

式中：A为弹体的横截面积；下标1表示已知弹道极限速度的弹靶系统的各物理量；下标2表示待求弹道极限速度的弹靶系统的各物理量。Inconel 718为GH4169的美国相近牌号，认为它们的抗侵彻性能一致，即弹体对相同面密度的Inconel 718与GH4169弹道极限比动能相等，预估得钨球(直径8 mm，质量4.7 g)对面密度为25.71 kg/m2的 GH4169靶板(厚度约3.12 mm)的弹道极限速度约为367.9 m/s。

2.2 实验结果

实验弹体采用直径8 mm钨合金球，以厚度为3 mm的GH4169板材作为靶板。根据2.1节中预估的弹道极限速度，设计了15发穿甲实验，弹体初始速度范围为260～520 m/s。逐个测量钨球和挤凿块质量、靶板厚度、钨球初速和余速以及挤凿块速度，对以上数据进行记录如表2所示。

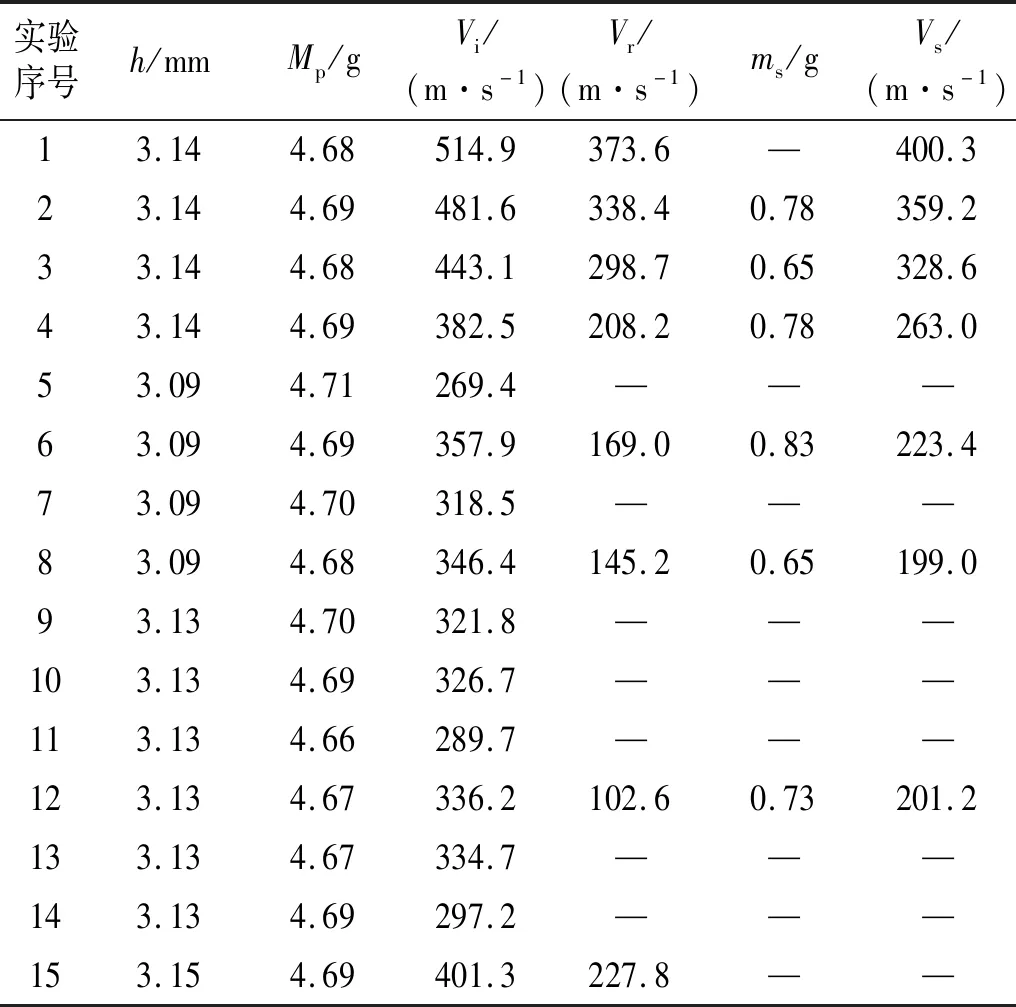
表2 φ8 mm钨球冲击3 mm厚GH4169靶板实验结果Tab.2 8 mm diameter tungsten ball impact 3 mm thick GH4169 plates experimental results

3 mm厚GH4169靶板在钨球冲击实验中未出现贯穿速度与未贯穿速度存在混合区，3 mm厚GH4169在钨球冲击实验中最低的贯穿速度(336.2 m/s)与最高的未贯穿速度(334.7 m/s)差值仅1.5 m/s，可用两弹初速平均值表示弹道极限速度，即V50=335.45 m/s。图3表示了实验中弹体余速和初速的关系，散点表示实验结果，通过Recht-Ipson模型拟合得到弹体初速和余速的关系曲线，如实线所示。从图3可以看出，随着弹体初速减小弹体初速和余速曲线的非线性度显著增加，在弹道极限速度附近，出现约100 m/s的弹体余速跳跃值。

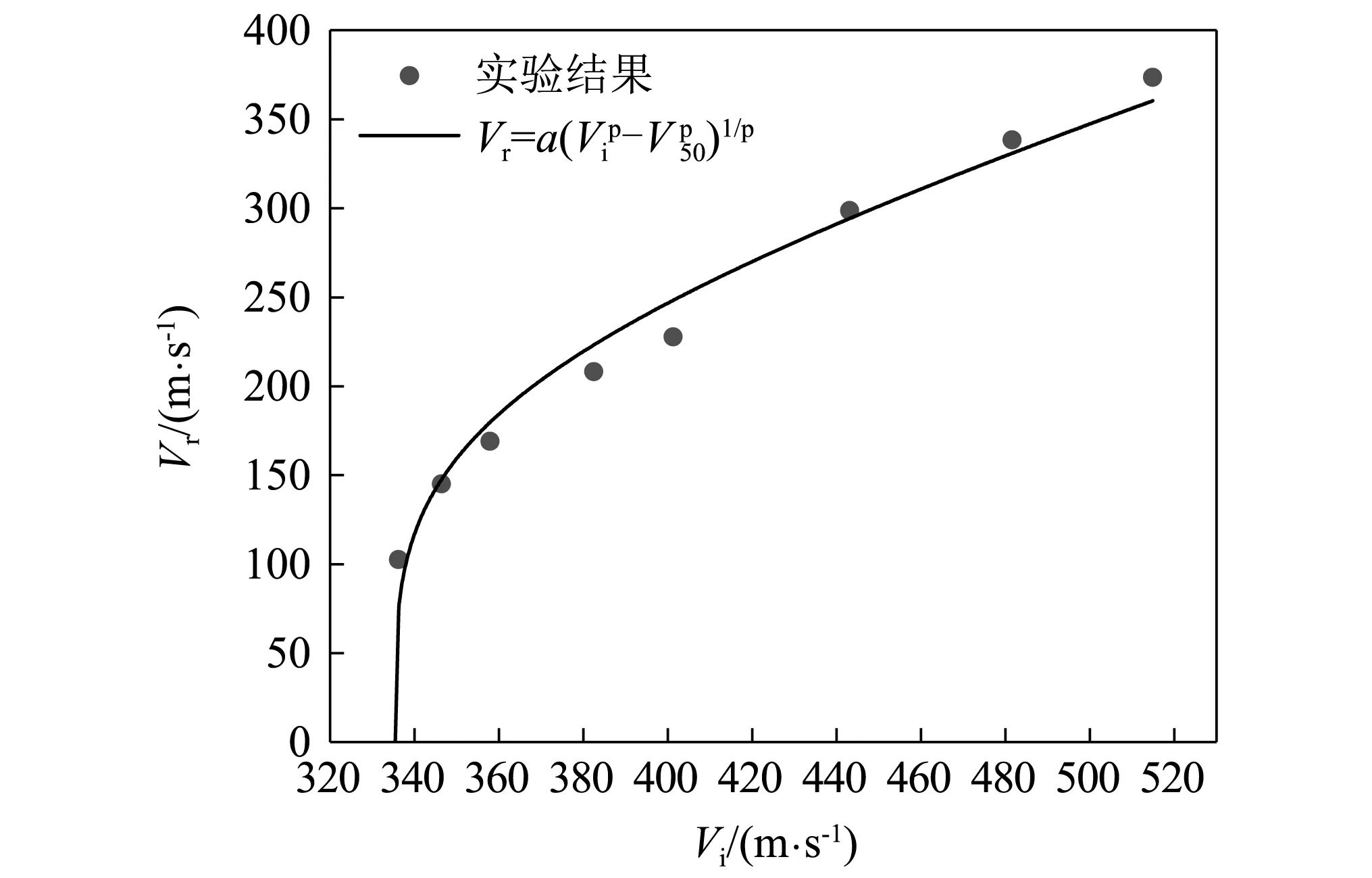
图3 3 mm厚GH4169靶板的弹体初速和余速关系Fig.3 Residual velocity curve for 3 mm thick GH4169 plates

图4为实验序号1中靶板的剖面图，明显看出圆形穿孔的背面有部分材料挤出而形成的环状凸起，该环状凸起的质量等于杯状挤凿块相对于柱状挤凿块所减少的质量。球形和半球形头弹体冲击中厚金属靶时认为靶板首先受拉应力作用而后才出现剪切，因此在冲击过程中产生了相对平头弹体贯穿中厚金属靶产生的柱状挤凿块质量较小的杯状挤凿块，挤凿块减少的质量均被弹体挤向靶板背面，从而形成环状凸起，并将杯状挤凿块简化为圆台以便对其质量进行计算。如图5所示，实验回收的典型杯状挤凿块尺寸明显小于穿靶后的钨球直径d，将杯状挤凿块等效为圆台，d1和d2分别为圆台的上下底面直径，另外，从表2可以看出挤凿块质量与钨球初速相关性不大。

图4 实验序号1中GH4169靶板截面Fig.4 Section of GH4169 plate in Exp.No1

图5 实验回收的钨球与典型挤凿块Fig.5 Recycled tungsten ball and typical plug

直径8 mm钨球正冲击3 mm厚GH4169靶板的实验结果发现挤凿块与弹体是分离的。实验中高速摄影拍到实验序号4中典型靶后钨球和挤凿块运动轨迹如图6所示，明显看出挤凿块比钨球运动更快，此发实验中钨球弹体初速382.5 m/s，余速208.2 m/s，挤凿块速度263.0 m/s。

图6 实验序号4中钨球和挤凿块相对位移Fig.6 Relative displacement of tungsten ball and plug in Exp.No 4

3 模型的验证与分析

通过文献[8]以及上述实验数据可对中厚金属靶的挤凿块速度模型在三种不同形状弹体(平头、半球形头、球形弹体)情况下进行验证。Børvik等通过基于激光的光学设备在轻气炮发射平头及半球形头的工具钢弹体(直径20 mm，质量0.197 kg)冲击厚度12 mm的Weldox 460 E钢靶板的实验中得到了弹体余速和挤凿块速度，平头弹体数据点如图7中“□”所示，半球形头弹体数据点如图7中 “△”所示。将钨球冲击GH4169靶板实验的弹体余速和挤凿块速度数据点如图7中 “○”所示。在实验范围内数据点均在直线Vs=Vr之上，表明挤凿块速度均大于弹体余速。基于式(5)对上述的弹体余速和挤凿块速度数据进行拟合得到不同类型刚性钝头弹体的k，Vsrjump如表3所示，后续可根据刚性钝头弹体的形状直接从表3中选取挤凿块速度模型的参数值。

将通过式(5)得到的挤凿块速度与弹体余速关系曲线绘制在图7中，与实验数据吻合很好，表明式(5)可很好的描述挤凿块速度与弹体余速的关系。将曲线横坐标延长至弹体余速等于0 m/s，此时对应一定的挤凿块速度，曲线与纵坐标轴的交点的纵坐标值表示了挤凿块速度相对于弹体余速为0时的跳跃值Vsrjump。

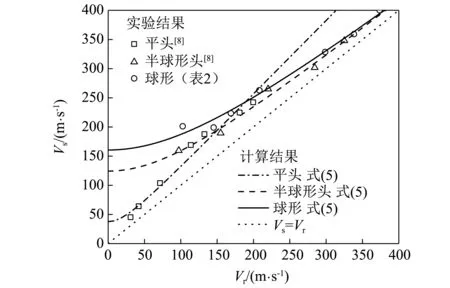
图7 弹体余速与挤凿块速度关系Fig.7 Residual velocity of projectiles and plug velocity

针对刚性钝头弹体(平头、半球形头、球形)正贯穿中厚金属靶的三组实验,图8给出不同弹靶条件下获得的弹体初速和挤凿块速度。将文献[8]以及表2中的弹体初速和挤凿块速度绘入图8中，平头弹体数据点如图8中“■”，半球形头弹体数据点如图8中“▲”，球形弹体数据点如图8中“●”。将弹体质量、弹体直径、靶板厚度、靶材密度等弹靶条件代入式(7)和式(8)得到ϑ和η，将ϑ和η及表3中的k和Vsjump一并代入挤凿块速度模型式(9)，得到3种弹靶条件对应的挤凿块速度与弹体初速曲线如图8中曲线所示。

图8 挤凿块速度模型与实验结果比较Fig.8 Comparison of the plug velocity model and experimental results

从图8可以看出，挤凿块速度模型的计算结果与实验数据具有很好的一致性，表明本文提出的挤凿块速度模型可以准确计算刚性钝头弹体(平头、半球形头、球形)正贯穿中厚金属靶射出的挤凿块速度(包括挤凿块在弹道极限速度附近出现的速度跳跃值Vsjump)。另外，对于三种刚性钝头弹体正贯穿中厚金属靶射出的挤凿块速度，平头弹体较于半球形头弹体和球形弹体穿靶后射出的挤凿块速度跳跃值Vsjump小得多，随着弹体初速的增加平头弹体对应的挤凿块速度上升更快，图8中曲线与实验数据的吻合程度正说明了挤凿块速度模型可对上述实验规律给出准确的预测。挤凿块速度模型实现了弹体贯穿中厚金属靶射出的挤凿块对靶后目标毁伤能力的定量描述，同时在多层间隔靶穿甲研究中，当弹体贯穿上一层靶板后，为计算下一层靶板的冲击工况给出了显式的理论计算模型。

4 结 论

刚性钝头弹体正贯穿中厚金属靶时，对于很多材料的靶板会射出与弹体余速不同速度的挤凿块，将挤凿块速度和弹体余速分开来考虑，首次建立了挤凿块速度的计算模型，主要完成了以下工作并得出如下结论：

(1)考虑了挤凿块形状与弹体形状(平头、半球形头、球形)相关，改进了中厚金属靶的剪切冲塞模型，改进后模型的应用范围从平头弹体扩展至半球形头弹体和球形弹体。基于能量守恒定律和改进后的剪切冲塞模型，建立了刚性钝头弹体正贯穿中厚金属靶的挤凿块速度模型。

(2)在钨球正冲击GH4169中厚金属靶实验中，应用高速摄影获得了弹体初速、弹体余速和挤凿块速度，回收挤凿块并测得挤凿块质量。通过实验结果和文献[8]中数据来验证提出的挤凿块速度模型，模型计算结果与实验数据具有很好的一致性。挤凿块速度模型可准确计算刚性钝头弹体正贯穿中厚金属靶所射出的挤凿块速度。

(3)挤凿块速度模型可以定量描述刚性钝头弹体(平头、半球形头、球形)正贯穿中厚金属靶射出的挤凿块对靶后目标的毁伤能力。同时，挤凿块速度模型可为多层间隔靶的穿甲研究提供一定的理论支撑。