服务外包长期合作机制的演化博弈分析

师亚玲

(淮北师范大学 经济与管理学院，安徽 淮北 235000)

0 引言

在新一轮信息技术推动下，作为企业融合运用全球资源的关键举措，服务外包已逐渐成为促进全球产业链重组的新动力. 然而，在国际方面，金融危机冲击的深度影响依然存在，全球经济在深层次改革中曲折复苏，增长乏力； 在国内方面，经济增长方式粗放，创新能力不足，以及传统竞争优势弱化等问题依然突出.

Abraham(亚伯拉罕)和Taylor[1](泰勒)通过研究发现，制造业企业把生产性服务外包出去有利于节约劳动力成本，缩短生产周期，促进生产专业化； 作家Friedman(弗里德曼)在其著作《世界是平的》中写道，服务外包是促进世界转变的最关键因素之一，世界正逐渐因服务外包而发生变革[2]. Kearney(卡尼)为了分析评价国际服务外包承包企业的竞争力，创建了各种指数与指标[3]Gonzalez(冈萨雷斯)等. Lopis将外包质量、成本大小、稳定性以及企业双方的相似度等要素归纳为影响承包企业的关键因素[4]. 在国内，申亮等通过构建演化博弈模型，结合系统动力学仿真，分析政府、外包商以及公众三方的协作达成，对我国当前公共服务外包的进一步推进具有一定的借鉴意义[5]. 刘春生等在分析了北京市在劳动力培养方面的挑战与机遇的基础上，总结别国在服务外包成功升级时的经验，指出北京市在发展服务外包时的路径选择[6]. 胡盛强等以Stackelberg(斯塔克伯格)博弈理论和古诺模型为研究方法，构建了各企业不合作、部分合作及完全合作情形下的最大化利润模型[7]； 张宗明等针对服务参与双方的努力程度无法验证以及服务商具有私有信息两种风险因素，提出区别服务商私有信息的委托代理模型，研究非对称信息下的最优契约[8].

以往对服务外包的分析大多数建立在绝对理性的基础上，并从静态的视角探讨了博弈决策者在服务外包中的决策过程以及怎样完成服务外包的协调. 然而在现实生活中，众多企业由于认知过程的约束，通常仅具有有限理性，企业双方需展开重复多次的博弈，在博弈最初通常不能达到最优决策，需利用效仿与学习，逐渐改善自身的决策策略，增强企业的服务外包竞争力. 由此，本文将尝试通过演化博弈的理论研究手段，动态地考虑服务外包协调成本以及利润策略对于发包方与承包方合作决策演化路径的作用，同时考虑政府的协调控制策略，分析维持外包系统演化到合作决策均衡状态下的政府补贴与惩罚需满足的取值范围，并试图探讨服务外包系统陷入到“囚徒困境”的问题.

1 服务外包演化博弈模型的构建

发包方与承包方在分析判断效能、理论推理效能以及记忆力等方面并不十分完备，某些才能较突出，某些才能则较弱[9]，企业决策者较难判断自身的决策是否能够达到自身利润的最大化，所以企业双方都具有进行合作与不合作两种策略选择. 在此假定发包方进行合作的概率为x，不进行合作的概率为1-x； 承包方进行合作的概率为y，不进行合作的概率为1-y. 发包方与承包方的博弈支付矩阵如表1所示.

表1 发包方与承包方演化博弈的支付矩阵

为便于下述分析，对模型设置与符号意义作以下解释：

(1)假定πm与πr分别为发包方与承包方采取独立决策时的利润.

(2)当发包方与承包方采取合作策略时，此时集中决策方式将使得服务外包过程获得超额利润Δπ，假定a为发包方取得超额利润的比例，承包方所获得的超额利润分配比例为1-a； 发包方与承包方在协调服务外包过程时所花费的成本为C，比如双方在沟通过程中所产生的某些通信费用与交通费用，以及服务外包过程的协调优化花费等，将b与1-b分别表示为发包方与承包方在协调费用中的支付比例. 同时在协调过程中服务外包总超额利润Δπ应高于其在协调过程中的总花费成本C，超额利润分配比例a与协调成本分配比例b的取值范围分别为a∈(0,1)，b∈(0,1)，而且发包方与承包方所获得的超额利润应高于其所花费的成本，表示为aΔπ-bC>0，(1-a)Δπ-(1-b)C>0.

(3)当发包方决定进行合作，而承包方未进行合作时，此时发包方需支付协调所产生的成本为bC，而因为承包方并未采取合作策略，造成该服务外包过程无法采取集中决策一体化形式，所以最终未获得超额利润，承包方的利润依旧为πr.

(4)当承包方决定进行合作，而发包方未进行合作时，此时承包方需支付协调所产生的成本为(1-b)C，而因为发包方并未采取合作策略，造成该服务外包过程无法采取集中决策一体化形式，所以最终未获得超额利润，发包方的利润依旧为πm.

1.1 服务外包演化稳定策略的求解

演化博弈双方决策方式动态变动程度是探讨有限理性博弈分析的重要环节，而动态变动程度由博弈双方进行某个决策时的概率以及进行此决策时的利润高于平均利润的程度所决定. 也就是说，对于发包方与承包方，需分析得出其进行合作决策时的期望利润，不合作决策时的期望利润，以及在两种决策时的整体平均利润. 求解过程表示如下：

从上述支付矩阵(表1)可知，在发包方采取合作决策时的期望利润(适应度)以及不采取合作策略时的期望利润(适应度)可分别表示为Emc=ayΔπ+πm-bC与Emu=πm，由此发包方所获得的平均期望利润(平均适应度)为Em=x(ayΔπ-bC)πm； 对于承包方而言，采取合作决策时的期望利润(适应度)为Erc=(1-a)xΔπ+πr-(1-b)C，不采取合作决策时的期望利润(适应度)为Erc=πr，因此承包方的平均期望利润(平均适应度)可表示为Er=y[(1-a)xΔπ-(1-b)C]+πr.

利用演化博弈理论[10]，发包方的复制动态方程可建立如下：

(1)

同理可知承包方的复制动态方程为

(2)

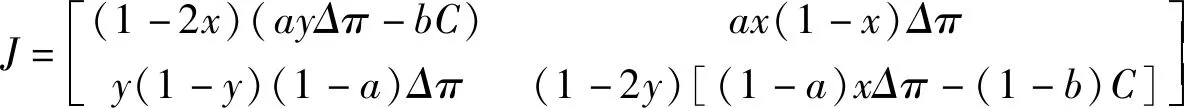
通过雅克比矩阵分析上述均衡点的部分稳定性可以得到[11-12]，如表2所示. 点O(0,0)与C(1,1)点为此博弈的演化稳定决策，而在点A(0,1)和B(1,0)处则不稳定，点D(xD,yD)为鞍点. 达到稳定点O(0,0)时，表示在服务外包过程中发包方与承包方考虑自身利润最大化采取独立决策策略； 稳定点C(1,1)表示在服务外包中发包方与承包方选择合作决策，且此时服务外包整体利润取得最大值. 最初状态所处的位置决定了外包系统最后演化到哪个均衡点. 如果初始状态在OADB范围内时最终将稳定于点O(0,0)，表示服务外包中的发包方和承包方同时采取不合作决策； 如果初始状态在ADBC范围内时最终将稳定于点C(1,1)，表示服务外包中的发包方和承包方同时采取合作决策，如图1所示.

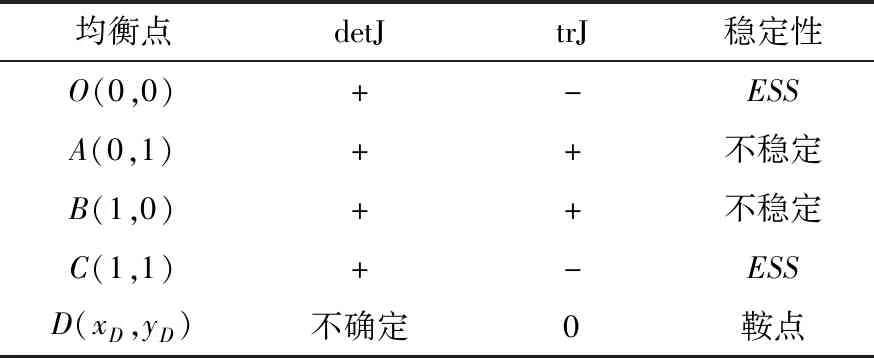
表2 均衡点的局部稳定性分析

图1 系统的演化博弈动态相位图

1.2 服务外包演化路径的影响因素分析

外包系统的演化为一个变动的过程，同时博弈利润分配矩阵的参数取值最终会对演化博弈的结论以及路径产生影响. 从图1可以看出，外包系统最终演化到点O(0,0)与C(1,1)的可能性由四边形OADB与ADBC的面积大小所决定，假设面积用S表示. 由此可知，分析博弈利润矩阵的参数取值对演化博弈结果产生的影响可等同于分析以上参数对OADB与ADBC面积大小的影响. 服务外包企业选择合作与不合作为两个相互对应的决策，仅需考虑各参数取值对于合作决策产生的影响即可. 可将ADBC范围内的面积表示如下：

SADBC=(1-yD)/2+(1-xD)/2

=1-(1-b)C/2(1-a)Δπ-bC/2aΔπ.

(1)服务外包协调成本对最终演化结果的作用.

通过对SADBC求解关于C的一阶偏导数可知，∂SADBC/∂C=-(1-b)/2(1-a)Δπ-b/2aΔπ<0，SADBC为关于C的单调递减函数.ADBC范围内的面积大小随着C的减小而逐渐增大，同时外包系统演化到稳定点C(1,1)的可能性增加，表明发包方与承包方进行合作决策的可能性增加.

结论1：发包方与承包方采取合作决策的概率随着服务外包协调成本的降低而逐渐增加.

(2)协调服务外包所得超额利润对最终演化结果的作用.

通过对SADBC求解关于Δπ的一阶偏导数可知，∂SADBC/∂Δπ=[(1-b)C/2(1-a)+bC/2a]Δπ2>0，SADBC为关于Δπ的单调递增函数，范围ADBC的面积大小随着Δπ的增加而逐渐增大，同时外包系统演化到稳定点C(1,1)的可能性增加，表明发包方与承包方进行合作决策的可能性增加.

结论2：发包方与承包方采取合作决策的概率随着协调服务外包所得超额利润的升高而逐渐增加.

(3)协调服务外包的成本分配参数对最终演化结果的作用.

通过对SADBC求解关于b的一阶偏导数可知，∂SADBC/∂b=C[1/(1-a)-1/a]2Δπ. 在a<1-a时，∂SADBC/∂b<0，表明SADBC的变化与b的大小呈负相关关系，范围ADBC的面积随着b的增长而逐渐减小，同时外包系统演化到稳定点C(1,1)的可能性减小，表明如果发包方所获得的超额利润比例小于承包方，同时当发包方所支付的协调成本增加时，发包方将结束合作，此时将导致服务外包的协调决策失败； 在a>1-a时，∂SADBC/∂b>0，表明SADBC的变化与b的大小呈正相关关系，范围ADBC的面积随着b的增长而逐渐增加，同时外包系统演化到稳定点C(1,1)的可能性增大，表明如果发包方所获得的超额利润比例大于承包方时，即使当发包方所支付的协调成本增加时，发包方也将继续保持合作，此时将使得服务外包的集中协调决策正常执行. 根据上述分析可知，为了实现服务外包的协调，同时获得服务外包系统的利润最大化，只有在发包方与承包方满足对超额利润所占分配比例与对协调成本的支付比例呈正比时，企业双方才认为公平，服务外包系统也将最终达成合作决策.

结论3：当制造企业对协调费用的支付比例增加时，对应的超额利润分配比例也将逐渐增大，同时服务外包系统进行合作决策的概率也将增加.

(4)协调服务外包的超额利润分配比例对最终演化结果的作用.

求解SADBC关于a的一阶偏导数可得，∂SADBC/∂a=C[b/a2-(1-b)/(1-a)2]2Δπ，进而求解SADBC关于a的二阶偏导数可知，∂2SADBC/∂a2=C[-2b/a3-2(1-b)/(1-a)3]/2Δπ<0，表明(0,1)区间内存在一个a的取值，使得SADBC达到极大值，此时外包系统演化到均衡点C(1,1)的概率最大，表明此时服务外包中的发包方与承包方可以通过一个最佳的超额利润分配指数，使得外包双方进行合作决策的意向达到最大.

结论4：通过协调找到一个最佳的超额利润分配指数，可使得发包方与承包方在服务外包系统中达到合作决策的概率最大.

2 服务外包在政府调节下的演化博弈分析

综上所述，服务外包系统最终会趋向于两个均衡点O(0,0)与C(1,1). 然而，由于服务外包决策者的有限理性，最终发包方与承包方的演化博弈结果极大可能采取不合作决策，导致整个外包系统陷入“囚徒困境”. 此时，为了取得服务外包系统整体利润最大化以及企业利润的帕累托改进，需要依靠政府的调节举措以确保服务外包的有效调节. 政府可以为企业搭建合作的沟通服务平台，以增强服务外包系统的市场效益与竞争力. 例如，为了增加企业之间相互合作的频率，可以为其供给服务测评、信息沟通与技术交流等支持. 在发包方与承包方采取合作决策时，需要支付一定的成本费用，此时政府可以提供一定的补贴政策来指导博弈参与企业进行合作，而在某一方未采取合作决策时，政府可对此企业采取一定的惩罚措施，以此来减少不合作行为发生的次数. 由此，政府的调节举措对演化博弈产生的作用可从补贴政策与惩罚措施两方面进行分析.

2.1 补贴政策下服务外包的演化博弈分析

对于发包方与承包方而言，在进行合作决策时，企业双方都应支付一定份额的成本费用，此时政府可采取补贴决策来促进服务外包系统采取合作策略. 在此将补贴额用R表示. 由此，服务外包企业的博弈支付矩阵可如表3所示.

从表3可知，对于发包方而言，当其进行合作决策的期望利润、不进行合作决策时的期望利润以及平均期望利润可分别表示为Emc=ayΔπ+πm-bC+R，Emu=πm和Em=x(ayΔπ-bC+R)+πm； 对于承包方而言，当其进行合作决策的期望利润、

表3 补贴政策下的发包方和承包方演化博弈的支付矩阵

不进行合作决策时的期望利润以及平均期望利润可分别表示为Erc=(1-a)xΔπ+πr-(1-b)C+R，Erc=πr和Er=y[(1-a)xΔπ-(1-b)C+R]+πr.

发包方和承包方的动态微分方程可分别表示为：

(3)

分析式(3)可得，在R>bC时，发包方的复制动态方程含有两个不动点x=0与x=1. 同时按照进化稳定决策的特征以及微分方程的“稳定性定理”可以得出，x=1，此时为发包方复制动态方程的进化稳定决策(如图2所示). 同理可知，根据式(4)，在R>(1-b)C时，y=1，此时为承包方复制动态方程的进化稳定决策，在此不再赘述.

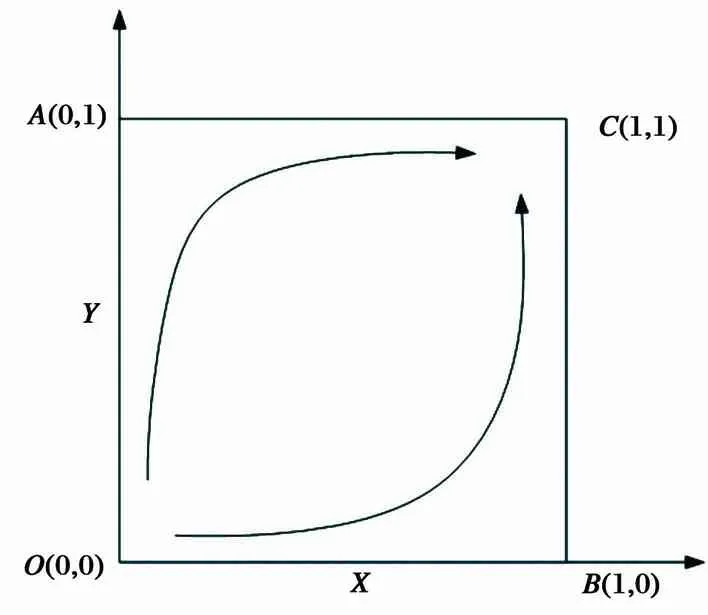
图2 发包方合作决策复制动态相位图

根据上述分析可得，在满足R>max[bC,(1-b)C] 时，外包系统将具有四个稳定点O(0,0)，A(0,1)，B(1,0)，C(1,1)，且C(1,1)为其中仅有的ESS，可以说明在政府提供给企业的补贴高于其需支付的服务外包协调费用时，发包方与承包方更愿意采取合作决策. 所以，政府需采取合理的补贴措施以促进服务外包企业之间的合作，降低企业不合作决策发生的可能性，以此来增加服务外包企业合作的概率，最终获得服务外包系统利润的最大化. 图3为此时的外包系统演化动态相位图.

图3 补贴政策下的系统演化动态相位图

2.2 惩罚措施下服务外包的演化博弈分析

当服务外包系统进行集中决策时，假如因为某一方拒绝采取合作决策，而对采取合作决策的另一方企业利润造成损失，严重打击了该企业选择合作决策的积极性，导致整个服务外包系统最终未协调成功. 此时，政府可以对未采取合作决策的博弈企业进行一定的惩罚措施P. 因此，可将这时发包方与承包方的博弈支付矩阵表示如表4所示.

表4 惩罚措施下的发包方和承包方演化博弈的支付矩阵

发包方承包方合作不合作合作πm+aΔπ-bC(1-a)Δπ+πr-(1-b)Cπm-bC,πr-P不合作πm-P,πr-(1-b)Cπm-P,πr-P

从表4可知，对于发包方而言，当其进行合作决策的期望利润、不进行合作决策时的期望利润以及平均期望利润可分别表示为Emc=ayΔπ+πm-bC，Emu=πm-P和Em=x(ayΔπ-bC+P)+πm-P； 对于承包方而言，当其进行合作决策的期望利润、不进行合作决策时的期望利润以及平均期望利润可分别表示为：

Erc=(1-a)xΔπ+πr-(1-b)C，Eru=πr-P和

Er=y[(1-a)xΔπ-(1-b)C+P]+πr-P.

发包方和承包方的动态微分方程可分别表示为：

(5)

(6)

分析式(5)可得，在P>bC时，发包方的复制动态方程含有两个不动点x=0与x=1，同时按照进化稳定决策的特征以及微分方程的“稳定性定理”可以得出，x=1，此时为发包方复制动态方程的进化稳定决策(如图2所示). 同理可知，根据式(6)，在P>(1-b)C时，y=1，此时为承包方复制动态方程的进化稳定决策，在此不再赘述.

根据上述分析可得，在满足P>max[bC,(1-b)C]时，外包系统将具有四个稳定点O(0,0)，A(0,1)，B(1,0)，C(1,1)，且C(1,1)为其中仅有的ESS. 可以表明，在服务外包系统中，假如政府对不合作企业采取惩罚措施时，该惩罚额应超出该博弈企业进行合作决策时需支付的费用，此时该博弈企业将愿意采取合作决策. 所以，政府需采取合理的惩罚措施，该惩罚数额需超过能够使得服务外包中的博弈企业进行合作决策所得利润高于未进行合作决策时的利润，此时的惩罚措施才能达到目的，从而降低企业不合作决策发生的可能性，以此来增加服务外包企业合作的概率，最终获得服务外包系统利润的最大化. 此时的服务外包系统演化动态相位图依然可用图3表示.

3 仿真分析

上述内容在理论上对于服务外包中的发包方与承包方合作决策的演化博弈做了探讨，为了进一步分析各个参数的变化对外包系统演化博弈产生的影响，接下来将通过仿真分析的方法对上述模型进行分析，进行更深入的探讨. 依据上述模型设定参数，假设超额利润Δπ=10 000，协调费用C=1 000，超额利润分配比例a=0.5，协调费用支付比例b=0.6. 下面的分析中，在讨论某个参数对合作决策的作用时，仅需改变该参数的取值区间即可.

例1 协调服务外包所花费的成本以及在协调后所取得的超额利润的大小将对外包系统演化到合作决策的可能性产生影响，所以需维持其他参数取值固定. 在[10 000,15 000]内变化Δπ的取值大小，在[1 000,1 500]内变化C的取值，分析在此时SADBC的变化范围.Δπ，C以及合作概率之间的相互关系可由图4与图5表示.

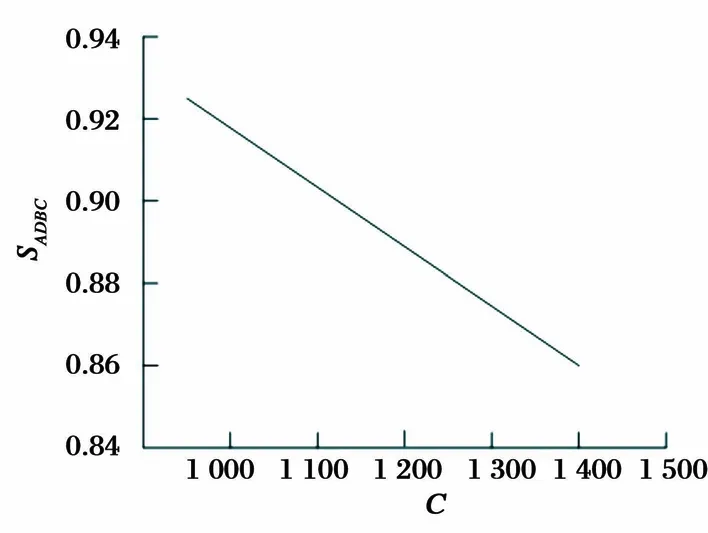
图4 C对合作概率的影响

图5 Δπ对合作概率的影响

从图4可以看出，服务外包系统进行合作决策的概率SADBC随着协调服务外包的费用C的逐渐增长而减小，表明增长的协调管理费用成为一种风险投资，打击了发包方与承包方合作的积极性； 从图5可以看出，在发包方与承包方认识到通过协调可使服务外包系统获得超额利润Δπ时，企业双方的合作意向逐渐增强，最终将达到在Δπ逐渐增加时，外包系统演化到合作决策的可能性也随之增加的状态. 这也与上述结论1、2相符.

例2 当发包方与承包方进行合作决策时，企业对成本费用的支付比例以及对利润的分配比例决定了企业双方的合作动机，所以当固定其他参数取值不变时，假设a在区间[0.1,0.9]内变化，b=0.2，0.4，0.6，0.8，分析这时SADBC的变化轨迹.a与b对合作概率的作用可由图6表示.

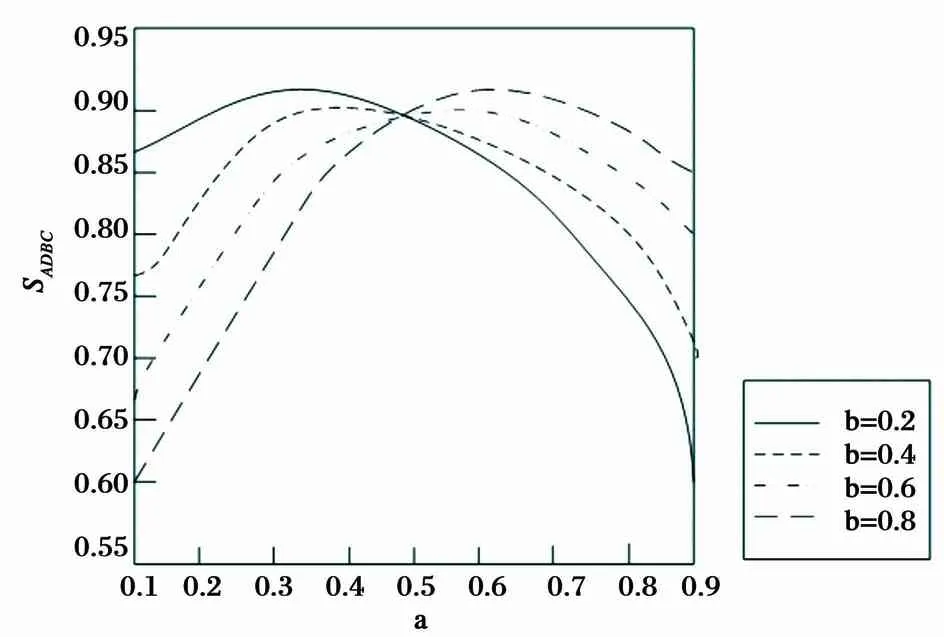
图6 a和b的变化对合作概率的影响

根据图6可以得到，当b分别为上述几种取值时，关于a的SADBC函数变化趋势均表现为“倒U形”，表明在b的各个取值中，含有某个可使SADBC取得极大值的a的最优取值，同时外包系统演化到合作决策的可能性达到最大. 在a>0.5时，随着b取值的增加，SADBC逐渐增大，表明在发包方取得的超额利润较大时，其支付的协调成本也逐渐增大，外包系统演化为合作决策的可能性增加； 在a<0.5时，随着b取值的增加，SADBC逐渐减小，表明在发包方取得的超额利润较小时，其支付的协调成本增大，企业双方进行合作的概率减小. 综上所述，在协调服务外包系统时，双方博弈企业取得的超额利润需与其支付的协调成本相对应，如此将维持合作的正常完成. 以上分析证明了结论3与4的合理性.

例3 在维持基本数据一定时，分析为保持外包系统演化到合作决策均衡状态时的政府补贴数与惩罚额的取值.

依据上述分析得出的政府补贴大小需满足R>max[bC,(1-b)C] ，然后代入参数取值可解得R>600，可知这时政府提供的补贴额超出服务外包企业所支付的成本费用，降低了服务外包企业进行合作决策时的风险大小，极大促进了发包方与承包方进行合作决策的积极性. 同理，惩罚额需满足P>max[bC,(1-b)C] ，然后代入参数取值可解得P>600，可知这时政府对不合作决策采取的惩罚程度高于发包方与承包方进行合作决策时所支付的费用，因此企业双方最终将采取合作决策. 综上所述，政府采取合理的调控决策可保障服务外包系统向着帕累托最优演化.

4 结语

由于发包方与承包方在理解认识方面具有某些制约，比如可能认知分析能力较低，同时未获取完整信息，企业双方较难决定自身的选择能否最终取得利润最大化，所以企业决策者都可选择进行合作与不合作两种决策. 鉴于此，本文依据演化博弈的复制动态方程，分析动态演化博弈的稳定点，紧接着探讨了影响演化路径变动的要素. 最后为了分析服务外包系统陷入到“囚徒困境”这一问题，提出了政府的调控措施，分析外包系统演化到合作决策均衡状态时政府的补贴大小以及惩罚举措需满足的要求.