指数保费原理中风险保费的变点推断

章 溢, 温利民, 李志龙

(1- 江西师范大学财政金融学院，南昌 330022;2- 江西师范大学数学与统计学院，南昌 330022; 3- 海南师范大学数学与统计学院，海口 571158;4- 海南师范大学大数据科学与智慧教育重点实验室，海口 571158)

1 引言

在非寿险精算中，如何为一份保单制定合适的价格是精算师的重要任务之一.对给定的风险随机变量X，制定的价格R(X)的方法常常称为保费原理.常用的保费原理包括期望值原理、方差原理、标准差原理、Esscher 保费原理、指数保费原理等.作为一种风险度量，保费原理R(X)一般需要满足正的安全负荷、对独立风险的可加性、对共同单调风险可加性、转移不变性等.Young[1]总结了各种保费原理满足哪些保费原理的性质，从文献的整理可以看出，除了净保费原理外，指数保费原理是满足最多“好”的性质的保费原理.因此，指数保费原理不仅保险公司得到广泛的运用，而且在理论上也引起了深入的研究[2,3].然而，在实际风险管理中，由于风险因素的复杂性，经过一段时间后由于环境、条件的变化，风险也可能发生变化.从而导致保费也需要相应的调整.因此，精算师有必要根据风险的观测值情况判断保费在某个时间点是否变动.事实上，变点统计推断是数理统计研究的热点问题之一.关于随机变量的均值、方差等的变点研究已经积累了大量的文献.早期的文献可参考文献[4-6].关于变点检测的统计方法有较多的讨论，例如，Bai[7]运用最小二乘法研究了时间序列中线性过程的变点估计，Xia 和Qiu[8]提出一种跳跃信息准则研究了回归曲线的变点统计推断问题，Bai 和Saranadasa[9]、Chen 和Qin[10]等利用矩阵的迹方法构造了高维数据中均值和方差的变点统计推断问题.近年来，随着大数据的提出和发展，变点检测和统计推断在现代统计推断中变得越来越重要[11-14].

然而，在非寿险精算中，已经有一定的文献研究风险模型中变点检测及其统计推断问题[15-18].本文将关注给定风险模型中由于风险的变化导致的指数保费的变点统计问题.若检测到风险发生变化，则显然要对风险的保费进行调整.因此保费的变点检测具有非常重要的实际意义.

对给定的风险X，以及相应的若干年的相互独立的样本观测值X1,X2,··· ,Xn.记Pi=R(Xi)表示风险Xi的指数保费.我们将检验下面的原假设

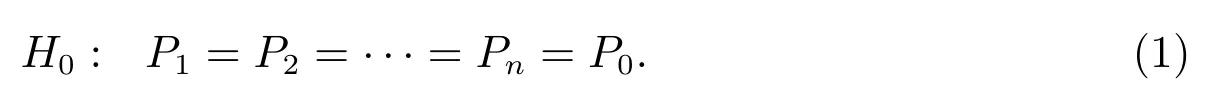
对备择假设

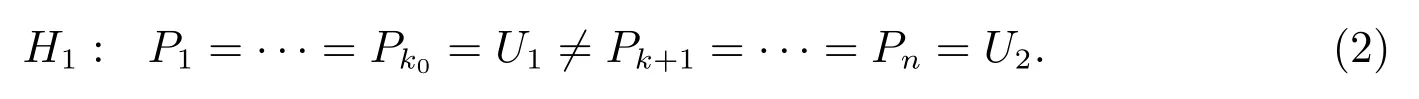
若拒绝原假设而接受备择假设H1，则显示风险X 的指数保费在k0位置出现变点.

文章的目的之一是给出变点位置的一个估计.进而，我们将构造统计量检验假设H0.本文的重点是研究指数保费变点估计的相合性和收敛速度.文章后面的内容安排如下.第2 节给出指数保费原理的相关介绍.第3 节给出变点的估计及其相应的统计性质.第4 节给出统计量的模拟结果，从数值上分析统计量的收敛速度情况.

2 指数保费原理及其变点估计模型

设集合χ 表示概率空间(Ω,F,P)中可保的非负风险随机变量集合.而X, Y, Z 表示可保风险，即为保险公司承保保单的损失额.记FX(x)为X 的分布函数.为了定义指数保费原理，本文假设风险X 具有指数阶的矩，即

其中α0为某个给定的正常数.

定义1 保费原理R 定义为从χ 到实直线[0,+∞]上的一个映射，常记为

设保险公司具有初始资产w，且保险公司的效用函数为u(·).保险公司承保了风险X 后将收到保费R(X)，且保费R(X)由下面的方程的解

方程(5)左边表示保险公司承保风险X 后的期望效用.因此方程(5)显示保险公司在承保前后具有等价的效用.在非寿险精算中，根据方程(5)得到的解R(X)来制定保费的方法称为期望效用保费原理.当w =0 时称为零效用保费原理.关于期望效用原理的介绍可参考文献[19,20]等.

尽管方程(5)有很好的经济学解释，但一般没有显示解.然而，若取指数效用函数

对任意α ∈[0,α0]，则期望效用方程(5)的解能表达为显示的形式

定义2 对风险随机变量X ∈χ，定义X 的指数保费原理为(7)，并称之为风险X 的指数保费.

根据文献[3]，指数保费R(X)满足正的风险附加、对独立风险可加性、无不合理附加费、极大损失性、转移不变性、单调性、保留一阶随机控制序和停止损失序、连续型等众多“好”的性质.从风险度量的角度来看，指数保费R(X)是一致性风险度量[21].本文不对指数保费原理的性质做进一步讨论，我们的目的是检验假设H0对H1并给出变点估计及其统计推断方法.

显然，在H0成立时，

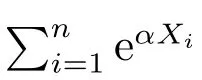
分别为P1和Pn的非参数估计.绝对偏差

反映了备择假设H1成立时指数保费在变点前后的差异.

则变点位置k0的估计可取为

当|T(k)|的最大值在多处同时达到时，估计取这些位置估计的最小值.

3 变点位置估计的大样本性质

一般地，我们有风险X 的n 个观测值X1,X2,··· ,Xn.首先，我们将确定风险X 的指数保费是否存在变点.即根据样本X1,X2,··· ,Xn的信息对假设H0对H1进行检验.注意到在H0成立时，有

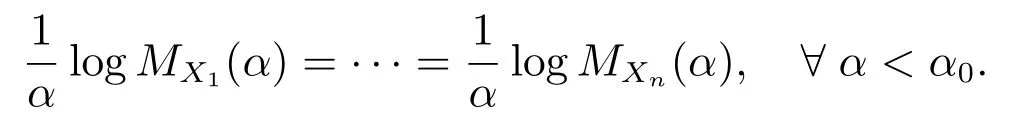
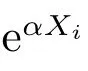
下面给出统计量T(k)在H0成立时的渐近分布.

定理1 若α ≤α0/2，当H0成立时，若n-→∞，则有

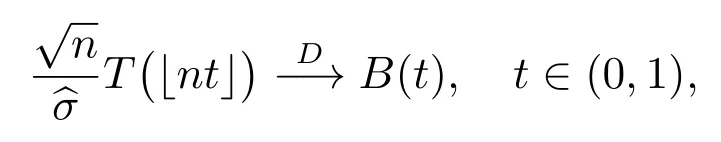
根据不变原则有

特别地，有

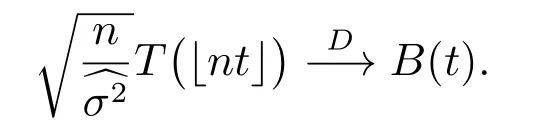
根据定理1，我们得到了原假设H0成立下统计量T(k)的分布.

注2 在定理1 条件成立时，根据连续性定理，则h(x)=suptx(t)是在空间D[0,1]上连续的，我们有

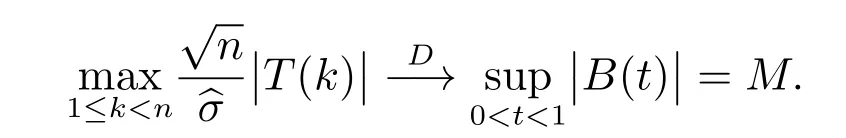
即为著名的Kolmogorov 分布.

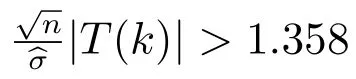
若原假设H0被拒绝，则显示指数保费R(X)在某处k0处存在变点，则可用(10)对变点位置k0进行估计，并证明变点估计(10)的大样本性质和收敛速度.

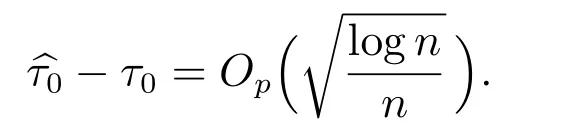
定理3 若对某个常数δ ＞0，有τ0∈(δ,1-δ)及k0/n-→τ0，则当H1成立时，有

综上所述，虽然教学改革的时间比较晚，但过程化教学的教学成果却很明显。合理的过程化教学有利于提高高校课堂教学任务以及课堂内容的完成效率，为民办高校学生以后的发展创造了条件。

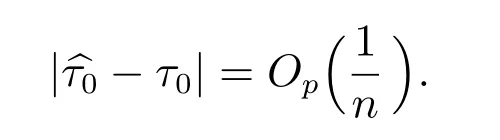
证明 对充分小的δ ＞0，根据推论1 以及τ0∈(0,1)可得

因此，对某个ε ＞0 以及充分大的n 有

为了证明(19)，只需证

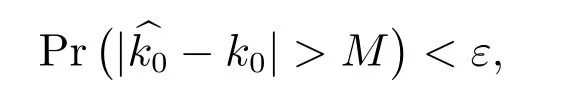
对ε ＞0 以及M =M(ε)成立.因为

我们定义下面的集合

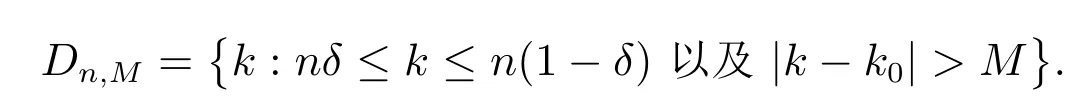
注意到

因此，只需证明

下面，我们将证明当n -→∞时，P1-→0 以及P2-→0.不损失一般性，假设k ≤k0，则由(12)得到

因此，有

由事件的分解和包含关系有

根据Chebyshev 不等式，有

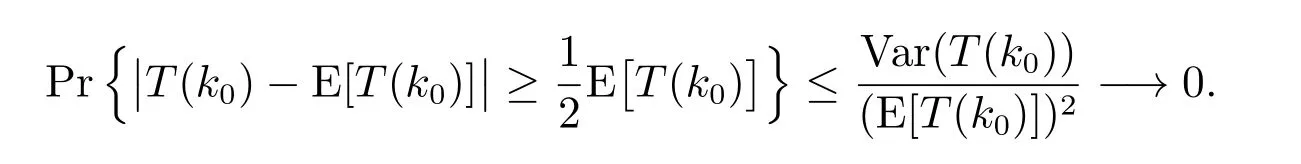
因此得到

另一方面，我们有

则有

以及

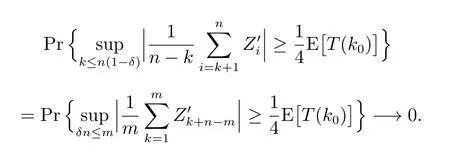
因此，有P1= Pr{T(k)-T(k0) ≥0} -→0.为了证明定理，则只需证明P2-→0 即可.类似地，根据对称性我们仅考虑k ≤k0.由式(14)得到

其中C1=Cλ.记S(k)=T(k)-E[T(k)]-(T(k0)-E[T(k0)])，则S(k)可以表达为

对k ∈Dn,M，通过事件的关系得到

因此，有

进而，根据下面的分解

并注意到|g(k)|≤1, |g(k)-g(k0)|≤C|k0-k|/n 对正常数C，有

因此得到

其中r =k0-k，而Ci, i=2,3,4 为不依赖n 的正常数. 根据Chebyshev 和Kolmogorov 不等式得到

以及

令r =k0-k，对M ≤r ≤k0以及对充分大的M 有

这表明P21-→0.对P22，由于|g(k)|≤1, |g(k)-g(k0)|≤C|k0-k|/n, n-k ＞n-k0，

将k0替换为nτ0，得到

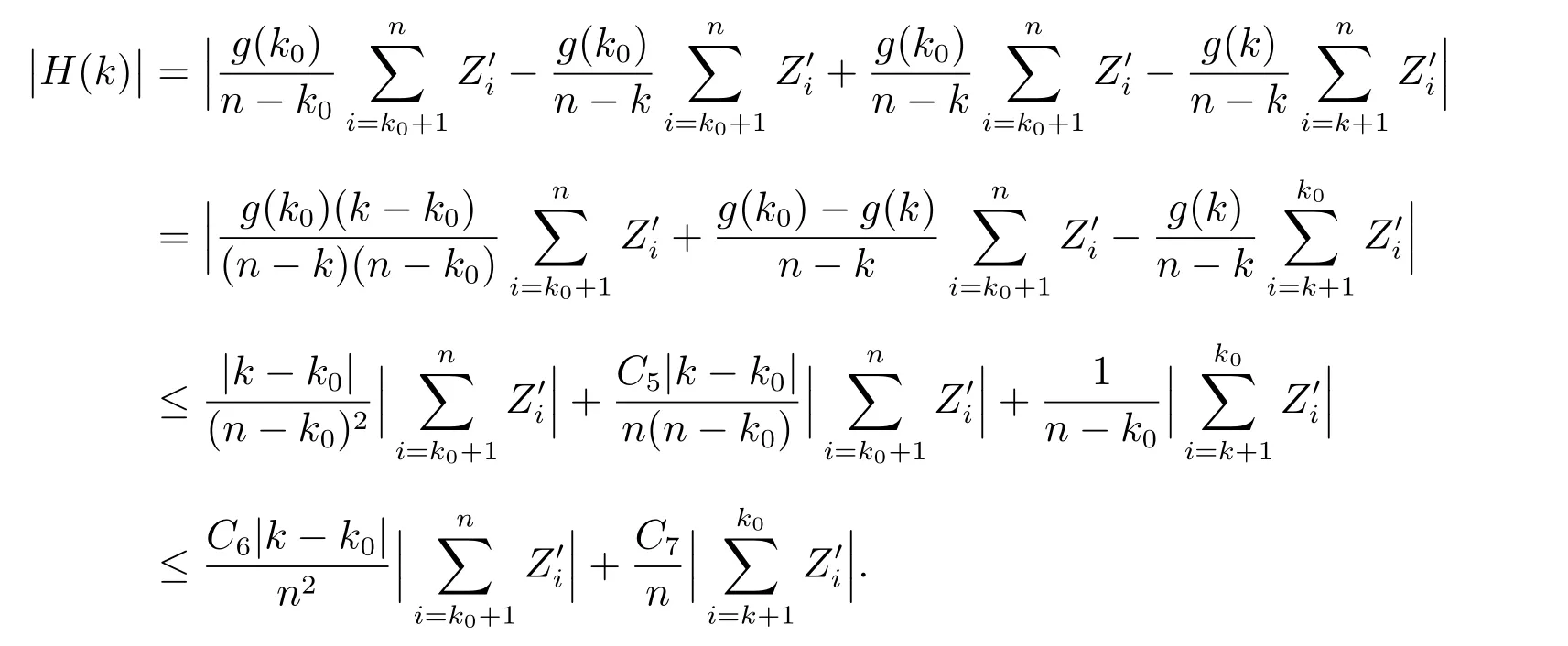
因此，有

对充分大的n 和M，上式最后两项均收敛到零.因此P22-→0，则完成了定理2 的证明.

注3 在风险理论中，文献[18]建立了风险度量中EVaR 的变点统计模型，并将变点估计方法运用金融传染模型，而文献[19]建立了具有变点理赔过程的风险模型，给出了风险存在变点时破产概率上界.然而，他们都没有给出变点估计的收敛速度，本文对风险X 建立了指数保费的统计模型，提出了变点是否存在的假设检验方法，并提出了基于指数保费的变点估计检测统计量，给出了变点估计的收敛速度.本文给出的方法能为保险公司的保费制定提供可供使用的参考价值和依据.

4 模拟研究

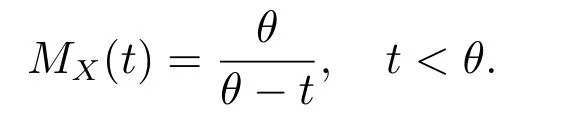
因此风险X 指数保费为

对不同的样本容量n，我们取α=0.3，在变点k0前后生成参数θ =2 和θ =6 的指数分布，计算指数保费P1,P2,··· ,Pn.根据变点估计(10)，对不同的的变点位置k0，计算精确度，经过10000 次重复模拟，得到下面三个表格，详见表1 至表3 所示.

表1 变点估计及其精确度(k0 =)

表1 变点估计及其精确度(k0 =)

n 10 20 40 80 200 400 800^k0 3.590 6.015 10.629 20.060 49.691 100.013 200.144 p 0.6441 0.7571 0.8339093 0.8979 0.9507 0.9759 0.9872

表2 变点估计及其精确度(k0 =)

表2 变点估计及其精确度(k0 =)

n 10 20 40 80 200 400 800^k0 4.181 8.522 17.513 36.941 96.402 195.821 395.693 p 0.7605 0.8118 0.8557 0.9116 0.9603 0.9775 0.9880

表3 变点估计及其精确度(k0 =)

表3 变点估计及其精确度(k0 =)

n 10 20 40 80 200 400 800^k0 4.823 10.598 22.893 50.469 135.531 282.697 579.723 p 0.6823 0.7055 0.7612 0.8401 0.9031 0.9420 0.9661